2024-2025学年华东师大版数学九年级上学期期末综合试卷(含答案)
文档属性
| 名称 | 2024-2025学年华东师大版数学九年级上学期期末综合试卷(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 618.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-12 14:46:51 | ||
图片预览



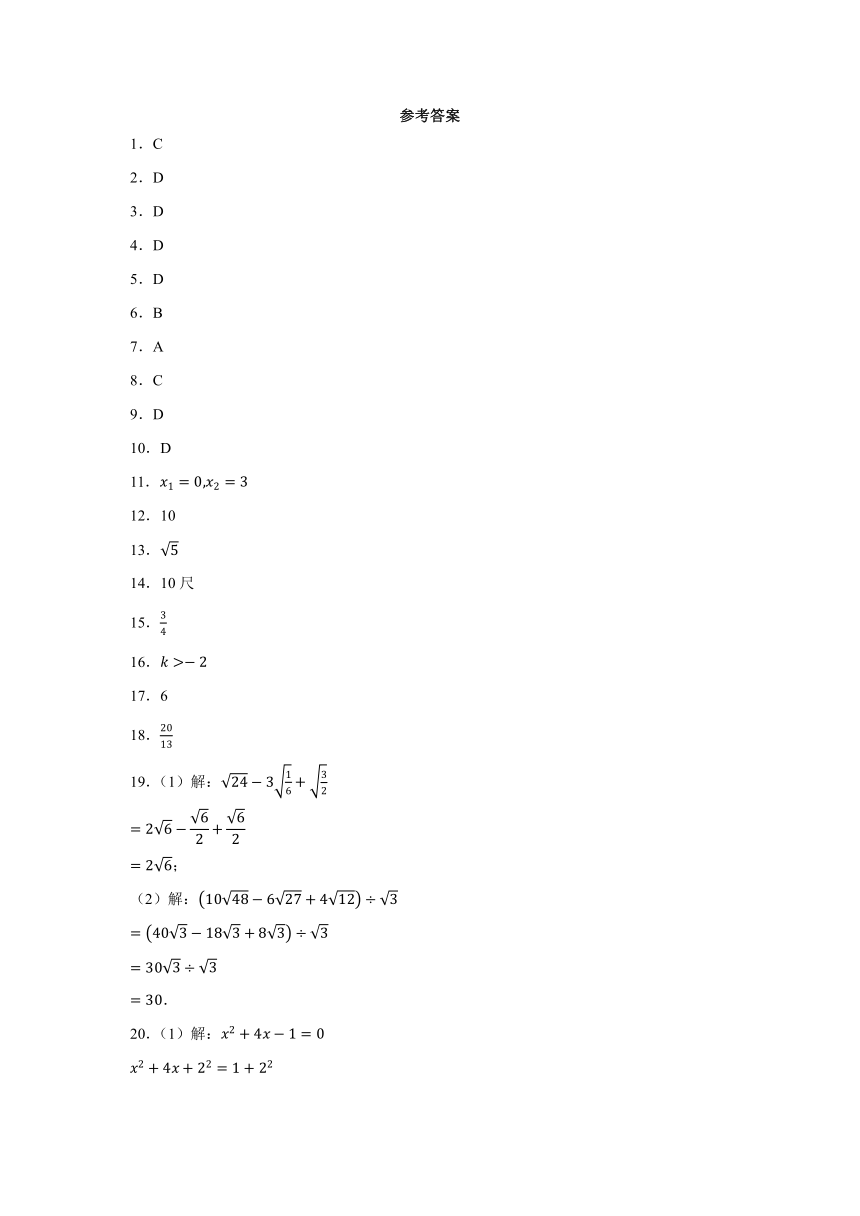
文档简介
2024-2025学年华东师大版数学九年级上学期期末综合试卷
学校:___________姓名:___________班级:___________学号:___________
一、单选题
1.下列方程中,关于x的一元二次方程的是( )
A. B. C. D.
2.在“离离原上草,一岁一枯荣”这古诗词中任选一个汉字,概率为是( )
A.离 B.草 C.一 D.离或一
3.下列各式计算正确的是( )
A.6﹣2=4 B.2+3=5
C.6÷2=3 D.2×3
4.如图,已知,且,则( )
A. B. C. D.
5.已知关于的一元二次方程的一个解是,则方程的另一个解为( )
A. B.2 C. D.3
6.如下图所示,一个小球由坡底沿着坡度为1∶2的坡面前进了10米,此时小球在竖直方向上上升了( )
A.4米 B.米
C.5米 D.米
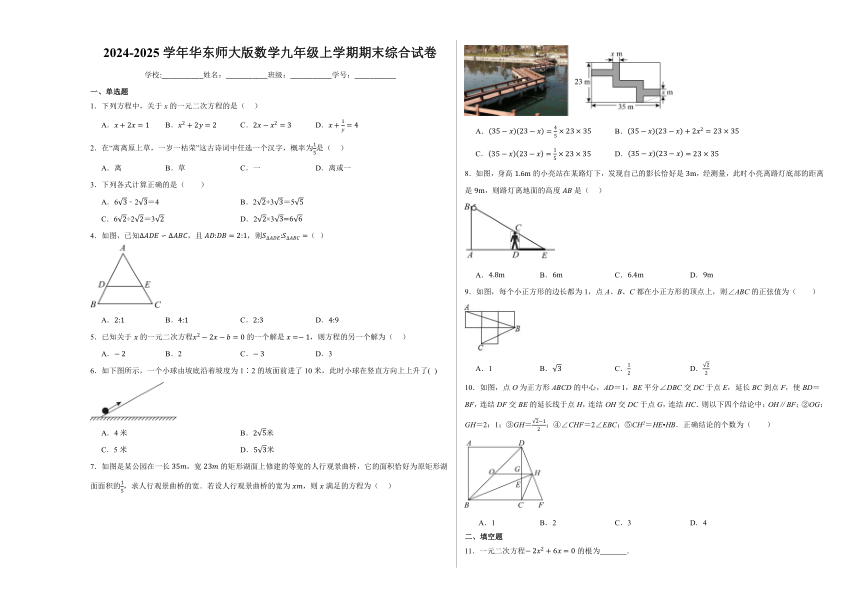
7.如图是某公园在一长,宽的矩形湖面上修建的等宽的人行观景曲桥,它的面积恰好为原矩形湖面面积的,求人行观景曲桥的宽.若设人行观景曲桥的宽为,则满足的方程为( )
A. B.
C. D.
8.如图,身高的小亮站在某路灯下,发现自己的影长恰好是,经测量,此时小亮离路灯底部的距离是,则路灯离地面的高度是( )
A. B. C. D.
9.如图,每个小正方形的边长都为1,点A、B、C都在小正方形的顶点上,则∠ABC的正弦值为( )
A.1 B. C. D.
10.如图,点O为正方形ABCD的中心,AD=1,BE平分∠DBC交DC于点E,延长BC到点F,使BD=BF,连结DF交BE的延长线于点H,连结OH交DC于点G,连结HC.则以下四个结论中:OH∥BF;②OG:GH=2:1;③GH=;④∠CHF=2∠EBC;⑤CH2=HE HB.正确结论的个数为( )
A.1 B.2 C.3 D.4
二、填空题
11.一元二次方程的根为 .
12.不透明的袋子里有50张2022年北京冬奥会宣传卡片,卡片上印有会徽、吉祥物冰墩墩、吉祥物雪融融图案,每张卡片只有一种图案,除图案不同外其余均相同,其中印有冰墩墩的卡片共有n张.从中随机摸出1张卡片,若印有冰墩墩图来的概率是,则n的值是 .
13.如图,在中,,,,则的长为 .
14.古算趣题:“笨人执竿要进屋,无奈门框拦住竹,横多四尺竖多二,没法急得放声哭. 有个邻居聪明者,教他斜竿对两角,笨伯依言试一试,不多不少刚抵足.借问竿长多少数,谁人算出我佩服.”试问竿长为 .
15.已知方程的两根的倒数和是,则 .
16.若关于的一元二次方程有两个不相等的实数根,则的取值范围是 .
17.一张等腰三角形纸片,底边长为,底边上的高长.现沿底边依次从下往上数剪宽度均为的矩形纸条,如图所示,已知剪得纸条中有一张是正方形,则这张正方形纸条是第 张
18.如图,在中,,,,点为边上一点,,将绕点旋转得到(点、、分别与点、、对应),使,边与边交于点,那么的长等于 .
三、解答题
19.计算:
(1) (2)
20.按要求解下列一元二次方程:
(1)(用配方法); (2)(用公式法).
21.某校组建了三个小组:A(经典诵读),B(诗词大赛),C(传统故事).学校规定:每名学生必须参加且只能参加其中一个小组.若该校小敏和小文两名同学各自从三个小组中随机选择一个小组,每一个小组被选中的可能性相同.
(1)小敏选择经典诵读小组的概率是 ;
(2)用画树状图或列表的方法,求小敏和小文选择不同小组的概率.
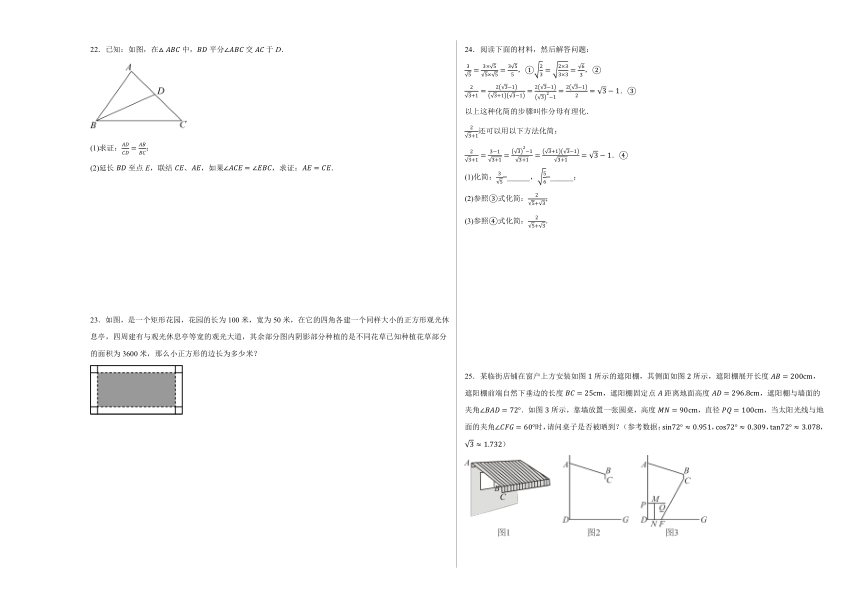
22.已知:如图,在中,平分交于D.
(1)求证:;
(2)延长至点E,联结、,如果,求证:.
23.如图,是一个矩形花园,花园的长为100米,宽为50米,在它的四角各建一个同样大小的正方形观光休息亭,四周建有与观光休息亭等宽的观光大道,其余部分图内阴影部分种植的是不同花草已知种植花草部分的面积为3600米,那么小正方形的边长为多少米?
24.阅读下面的材料,然后解答问题:
,①,②
.③
以上这种化简的步骤叫作分母有理化.
还可以用以下方法化简:
.④
(1)化简:=______,=______;
(2)参照③式化简:;
(3)参照④式化简:.
25.某临街店铺在窗户上方安装如图所示的遮阳棚,其侧面如图所示,遮阳棚展开长度,遮阳棚前端自然下垂边的长度,遮阳棚固定点距离地面高度,遮阳棚与墙面的夹角.如图所示,靠墙放置一张圆桌,高度,直径,当太阳光线与地面的夹角时,请问桌子是否被晒到?(参考数据:,,,)
26.爱好思考的小茜在探究两条直线的位置关系查阅资料时,发现了“中垂三角形”,即两条中线互相垂直的三角形称为“中垂三角形”.如图(1)、图(2)、图(3)中,AM、BN是△ABC的中线,AM⊥BN于点P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.
【特例探究】
(1)如图1,当tan∠PAB=1,c=4时,a= ,b= ;
如图2,当∠PAB=30°,c=2时,a= ,b= ;
【归纳证明】
(2)请你观察(1)中的计算结果,猜想a2、b2、c2三者之间的关系,用等式表示出来,并利用图3证明你的结论.
【拓展证明】
(3)如图4, ABCD中,E、F分别是AD、BC的三等分点,且AD=3AE,BC=3BF,连接AF、BE、CE,且BE⊥CE于E,AF与BE相交点G,AD=3,AB=3,求AF的长.
参考答案
1.C
2.D
3.D
4.D
5.D
6.B
7.A
8.C
9.D
10.D
11.
12.10
13.
14.10尺
15.
16.
17.6
18.
19.(1)解:
;
(2)解:
.
20.(1)解:
,
∴,;
(2)解:,
,
∴方程有两个不相等的实数根,
∴,
∴,.
21.(1)解:共三个活动小组,
小敏选择经典诵读小组的概率是.
(2)解:画树状图如下:
由树状图可知,共有9种等可能的结果,其中小敏和小文选择不同小组的结果有6种,
小敏和小文选择不同小组的概率为.
22.(1)证明:过点C作交的延长线于点H,
∵平分,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∴;
(2)如图,
∵,,
∴,
∵,
∴ ,
∴,
∵,
∴ ,
∴,
∴,
∴.
23.解:设小正方形的边长为x米,
由题意得,,
整理得:,
解得或(舍去),
答:小正方形的边长为5米.
24.(1)解:
;
(2);
(3).
25.解:如图,作于,于,延长交于,则,
由题意知:,,
∴四边形,四边形是矩形,
由题意得:,
在中,
∵,,
∴,
,
∴,
∴,
延长交于,交于,
由题意知:,,
∴,,
∴四边形,四边形是矩形,
∴,,
∴,
在中,,
∴,
∵,
∴桌子晒不到.
26.解:(1)解:如图1中,∵CE=AE,CF=BF,
∴EF∥AB,EF=AB=2,
∵tan∠PAB=1,
∴∠PAB=∠PBA=∠PEF=∠PFE=45°,
∴PF=PE=2,PB=PA=4,
∴AE=BF=.
∴b=AC=2AE=4,a=BC=4.
如图2中,连接EF,
,∵CE=AE,CF=BF,
∴EF∥AB,EF=AB=1,
∵∠PAB=30°,
∴PB=1,PA=,
在RT△EFP中,∵∠EFP=∠PAB=30°,
∴PE=,PF=,
∴AE=,BF=,
∴a=BC=2BF=,b=AC=2AE=,
(2)结论
证明:如图3中,连接EF.
∵AF、BE是中线,
∴EF∥AB,EF=AB,
∴△FPE∽△APB,
∴,
设FP=x,EP=y,则AP=2x,BP=2y,
∴a2=BC2=4BF2=4(FP2+BP2)=4x2+16y2,
b2=AC2=4AE2=4(PE2+AP2)=4y2+16x2,
c2=AB2=AP2+BP2=4x2+4y2,
∴a2+b2=20x2+20y2=5(4x2+4y2)=5c2.
(3)解:如图4中,在△AGE和△FGB中,
,
∴△AGE≌△FGB,
∴BG=FG,取AB中点H,连接FH并且延长交DA的延长线于P点,
同理可证△APH≌△BFH,
∴AP=BF,PE=CF=2BF,
即PE∥CF,PE=CF,
∴四边形CEPF是平行四边形,
∴FP∥CE,
∵BE⊥CE,
∴FP⊥BE,即FH⊥BG,
∴△ABF是中垂三角形,
由(2)可知AB2+AF2=5BF2,
∵AB=3,BF=AD=,
∴9+AF2=5×()2,
∴AF=4.
学校:___________姓名:___________班级:___________学号:___________
一、单选题
1.下列方程中,关于x的一元二次方程的是( )
A. B. C. D.
2.在“离离原上草,一岁一枯荣”这古诗词中任选一个汉字,概率为是( )
A.离 B.草 C.一 D.离或一
3.下列各式计算正确的是( )
A.6﹣2=4 B.2+3=5
C.6÷2=3 D.2×3
4.如图,已知,且,则( )
A. B. C. D.
5.已知关于的一元二次方程的一个解是,则方程的另一个解为( )
A. B.2 C. D.3
6.如下图所示,一个小球由坡底沿着坡度为1∶2的坡面前进了10米,此时小球在竖直方向上上升了( )
A.4米 B.米
C.5米 D.米
7.如图是某公园在一长,宽的矩形湖面上修建的等宽的人行观景曲桥,它的面积恰好为原矩形湖面面积的,求人行观景曲桥的宽.若设人行观景曲桥的宽为,则满足的方程为( )
A. B.
C. D.
8.如图,身高的小亮站在某路灯下,发现自己的影长恰好是,经测量,此时小亮离路灯底部的距离是,则路灯离地面的高度是( )
A. B. C. D.
9.如图,每个小正方形的边长都为1,点A、B、C都在小正方形的顶点上,则∠ABC的正弦值为( )
A.1 B. C. D.
10.如图,点O为正方形ABCD的中心,AD=1,BE平分∠DBC交DC于点E,延长BC到点F,使BD=BF,连结DF交BE的延长线于点H,连结OH交DC于点G,连结HC.则以下四个结论中:OH∥BF;②OG:GH=2:1;③GH=;④∠CHF=2∠EBC;⑤CH2=HE HB.正确结论的个数为( )
A.1 B.2 C.3 D.4
二、填空题
11.一元二次方程的根为 .
12.不透明的袋子里有50张2022年北京冬奥会宣传卡片,卡片上印有会徽、吉祥物冰墩墩、吉祥物雪融融图案,每张卡片只有一种图案,除图案不同外其余均相同,其中印有冰墩墩的卡片共有n张.从中随机摸出1张卡片,若印有冰墩墩图来的概率是,则n的值是 .
13.如图,在中,,,,则的长为 .
14.古算趣题:“笨人执竿要进屋,无奈门框拦住竹,横多四尺竖多二,没法急得放声哭. 有个邻居聪明者,教他斜竿对两角,笨伯依言试一试,不多不少刚抵足.借问竿长多少数,谁人算出我佩服.”试问竿长为 .
15.已知方程的两根的倒数和是,则 .
16.若关于的一元二次方程有两个不相等的实数根,则的取值范围是 .
17.一张等腰三角形纸片,底边长为,底边上的高长.现沿底边依次从下往上数剪宽度均为的矩形纸条,如图所示,已知剪得纸条中有一张是正方形,则这张正方形纸条是第 张
18.如图,在中,,,,点为边上一点,,将绕点旋转得到(点、、分别与点、、对应),使,边与边交于点,那么的长等于 .
三、解答题
19.计算:
(1) (2)
20.按要求解下列一元二次方程:
(1)(用配方法); (2)(用公式法).
21.某校组建了三个小组:A(经典诵读),B(诗词大赛),C(传统故事).学校规定:每名学生必须参加且只能参加其中一个小组.若该校小敏和小文两名同学各自从三个小组中随机选择一个小组,每一个小组被选中的可能性相同.
(1)小敏选择经典诵读小组的概率是 ;
(2)用画树状图或列表的方法,求小敏和小文选择不同小组的概率.
22.已知:如图,在中,平分交于D.
(1)求证:;
(2)延长至点E,联结、,如果,求证:.
23.如图,是一个矩形花园,花园的长为100米,宽为50米,在它的四角各建一个同样大小的正方形观光休息亭,四周建有与观光休息亭等宽的观光大道,其余部分图内阴影部分种植的是不同花草已知种植花草部分的面积为3600米,那么小正方形的边长为多少米?
24.阅读下面的材料,然后解答问题:
,①,②
.③
以上这种化简的步骤叫作分母有理化.
还可以用以下方法化简:
.④
(1)化简:=______,=______;
(2)参照③式化简:;
(3)参照④式化简:.
25.某临街店铺在窗户上方安装如图所示的遮阳棚,其侧面如图所示,遮阳棚展开长度,遮阳棚前端自然下垂边的长度,遮阳棚固定点距离地面高度,遮阳棚与墙面的夹角.如图所示,靠墙放置一张圆桌,高度,直径,当太阳光线与地面的夹角时,请问桌子是否被晒到?(参考数据:,,,)
26.爱好思考的小茜在探究两条直线的位置关系查阅资料时,发现了“中垂三角形”,即两条中线互相垂直的三角形称为“中垂三角形”.如图(1)、图(2)、图(3)中,AM、BN是△ABC的中线,AM⊥BN于点P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.
【特例探究】
(1)如图1,当tan∠PAB=1,c=4时,a= ,b= ;
如图2,当∠PAB=30°,c=2时,a= ,b= ;
【归纳证明】
(2)请你观察(1)中的计算结果,猜想a2、b2、c2三者之间的关系,用等式表示出来,并利用图3证明你的结论.
【拓展证明】
(3)如图4, ABCD中,E、F分别是AD、BC的三等分点,且AD=3AE,BC=3BF,连接AF、BE、CE,且BE⊥CE于E,AF与BE相交点G,AD=3,AB=3,求AF的长.
参考答案
1.C
2.D
3.D
4.D
5.D
6.B
7.A
8.C
9.D
10.D
11.
12.10
13.
14.10尺
15.
16.
17.6
18.
19.(1)解:
;
(2)解:
.
20.(1)解:
,
∴,;
(2)解:,
,
∴方程有两个不相等的实数根,
∴,
∴,.
21.(1)解:共三个活动小组,
小敏选择经典诵读小组的概率是.
(2)解:画树状图如下:
由树状图可知,共有9种等可能的结果,其中小敏和小文选择不同小组的结果有6种,
小敏和小文选择不同小组的概率为.
22.(1)证明:过点C作交的延长线于点H,
∵平分,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∴;
(2)如图,
∵,,
∴,
∵,
∴ ,
∴,
∵,
∴ ,
∴,
∴,
∴.
23.解:设小正方形的边长为x米,
由题意得,,
整理得:,
解得或(舍去),
答:小正方形的边长为5米.
24.(1)解:
;
(2);
(3).
25.解:如图,作于,于,延长交于,则,
由题意知:,,
∴四边形,四边形是矩形,
由题意得:,
在中,
∵,,
∴,
,
∴,
∴,
延长交于,交于,
由题意知:,,
∴,,
∴四边形,四边形是矩形,
∴,,
∴,
在中,,
∴,
∵,
∴桌子晒不到.
26.解:(1)解:如图1中,∵CE=AE,CF=BF,
∴EF∥AB,EF=AB=2,
∵tan∠PAB=1,
∴∠PAB=∠PBA=∠PEF=∠PFE=45°,
∴PF=PE=2,PB=PA=4,
∴AE=BF=.
∴b=AC=2AE=4,a=BC=4.
如图2中,连接EF,
,∵CE=AE,CF=BF,
∴EF∥AB,EF=AB=1,
∵∠PAB=30°,
∴PB=1,PA=,
在RT△EFP中,∵∠EFP=∠PAB=30°,
∴PE=,PF=,
∴AE=,BF=,
∴a=BC=2BF=,b=AC=2AE=,
(2)结论
证明:如图3中,连接EF.
∵AF、BE是中线,
∴EF∥AB,EF=AB,
∴△FPE∽△APB,
∴,
设FP=x,EP=y,则AP=2x,BP=2y,
∴a2=BC2=4BF2=4(FP2+BP2)=4x2+16y2,
b2=AC2=4AE2=4(PE2+AP2)=4y2+16x2,
c2=AB2=AP2+BP2=4x2+4y2,
∴a2+b2=20x2+20y2=5(4x2+4y2)=5c2.
(3)解:如图4中,在△AGE和△FGB中,
,
∴△AGE≌△FGB,
∴BG=FG,取AB中点H,连接FH并且延长交DA的延长线于P点,
同理可证△APH≌△BFH,
∴AP=BF,PE=CF=2BF,
即PE∥CF,PE=CF,
∴四边形CEPF是平行四边形,
∴FP∥CE,
∵BE⊥CE,
∴FP⊥BE,即FH⊥BG,
∴△ABF是中垂三角形,
由(2)可知AB2+AF2=5BF2,
∵AB=3,BF=AD=,
∴9+AF2=5×()2,
∴AF=4.
