浙江省临海市杜桥中学高中数学选修2-1课件:2.4.1 抛物线及其标准方程(一)(共11张PPT)
文档属性
| 名称 | 浙江省临海市杜桥中学高中数学选修2-1课件:2.4.1 抛物线及其标准方程(一)(共11张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 494.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-18 00:00:00 | ||
图片预览

文档简介
课件11张PPT。2.4.1抛物线及其
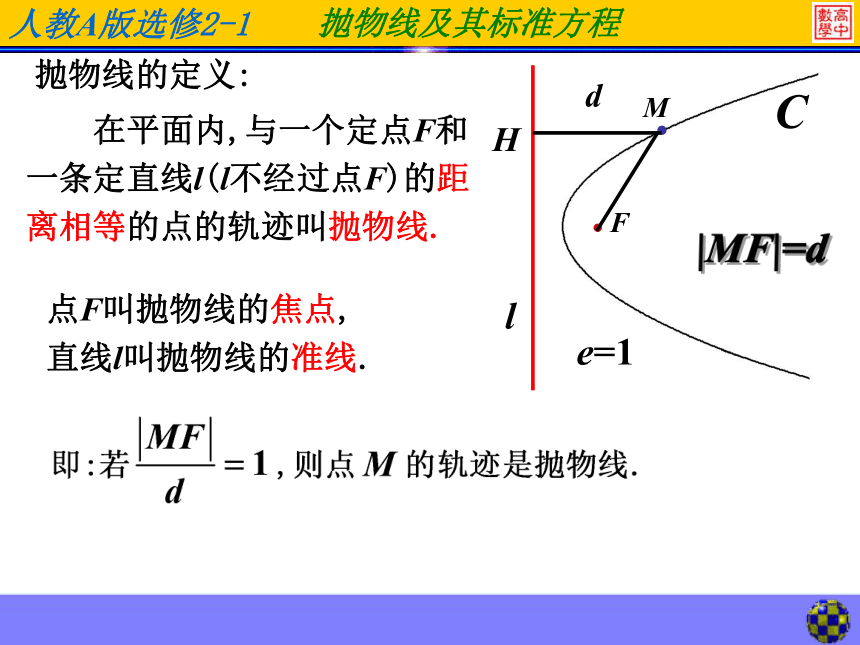
标准方程 在平面内,与一个定点F和一条定直线l(l不经过点F)的距离相等的点的轨迹叫抛物线.点F叫抛物线的焦点,
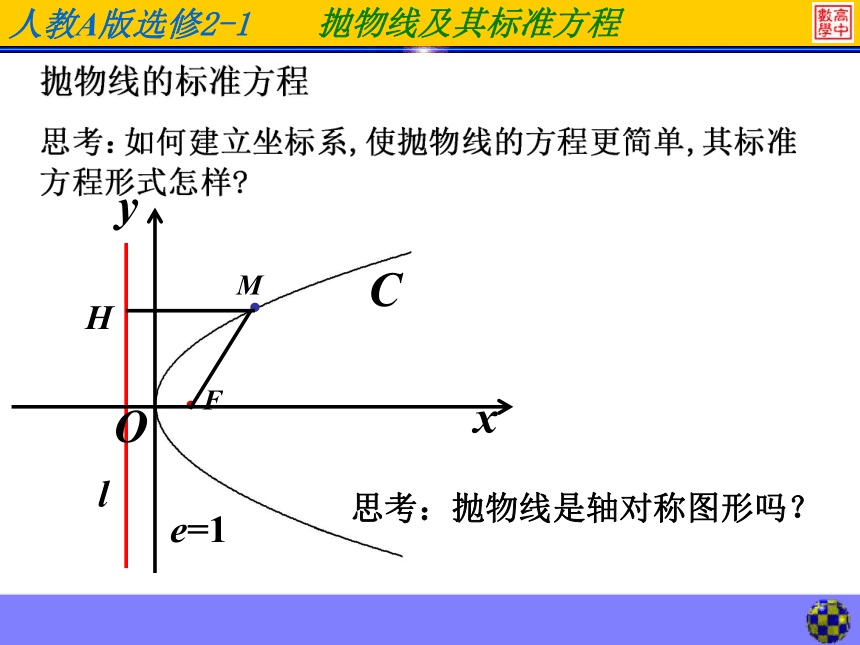
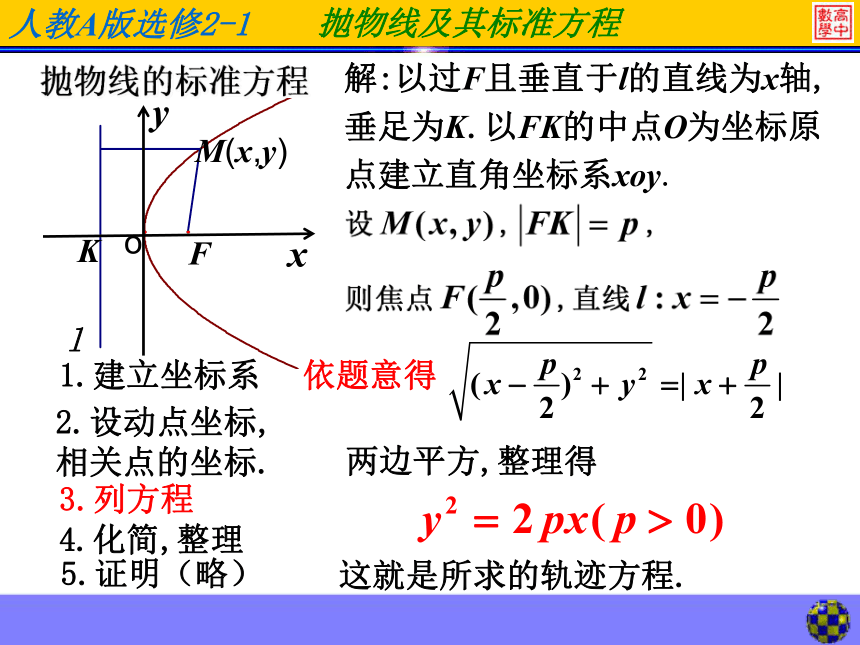
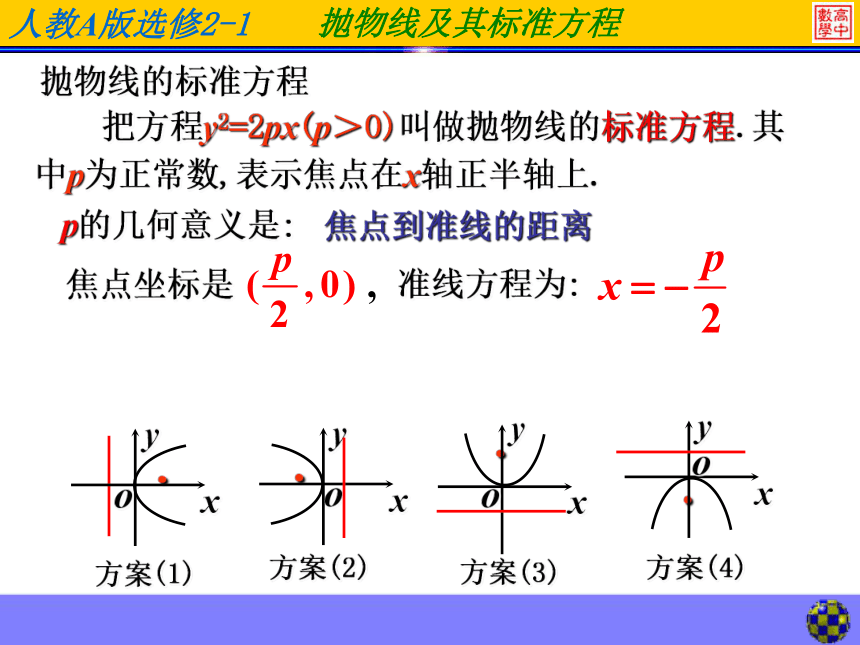
直线l叫抛物线的准线.|MF|=dd抛物线的定义:抛物线的标准方程思考:抛物线是轴对称图形吗?l解:以过F且垂直于l的直线为x轴,垂足为K.以FK的中点O为坐标原点建立直角坐标系xoy.两边平方,整理得M(x,y)F依题意得这就是所求的轨迹方程.1.建立坐标系2.设动点坐标,相关点的坐标.3.列方程4.化简,整理5.证明(略)抛物线的标准方程 把方程y2=2px(p>0)叫做抛物线的标准方程.其中p为正常数,表示焦点在x轴正半轴上. p的几何意义是:焦点坐标是准线方程为:焦点到准线的距离抛物线的标准方程P的意义:抛物线的焦点到准线的距离四种抛物线的对比方程的特点:(1)左边是二次式(2)右边是一次式,(3)一次项的系数
的正负决定了开
口方向.决定了焦点的位
置.如何判断抛物线的焦点位置,开口方向?⑴一次项的变量如为x(或y),则焦点就在x轴(或y轴)上; ⑵一次项的系数的正负决定了开口方向。例1:求下列抛物线的焦点坐标和准线方程:
⑴y2 =6x
⑵y2 =-6x
⑶y=6x2注:求抛物线的焦点一定要先把抛物线化为标准形式,后定焦点、开口及准线.⑴焦点坐标是F(0,-2);⑵准线方程为x = 1;⑹过点A(-3,2).x2 =-8yy2 =-4x例2.根据下列条件,求抛物线的标准方程.⑶焦点在x轴上,焦点到准线的距离为2;⑷焦点到准线的距离为2;⑸焦点在直线3x-4y-12=0上y2=±4xy2=±4x或x2=±4yy2=16x或x2=-12y⑺焦点在x轴上,抛物线上的点M(-3,m)到焦点的距离等于5.y2 =12xy2 =xy2 =±4x、x2 =±4y练2.求下列抛物线的焦点坐标和准线方程:
(1)y2 = 20x (2)x2= y
(3)2y2 +5x =0 (4)x2 +8y =0(5,0)x=-5(0,-2)y=2例3.若直线l:y=kx-2与抛物线y2=8x交于A、B两点,且AB中点的横坐标为2,求此直线l的方程.②以①中的弦为底边,以x轴上的点P为顶点作三角形,当三角形的面积为9时,求点P坐标.
标准方程 在平面内,与一个定点F和一条定直线l(l不经过点F)的距离相等的点的轨迹叫抛物线.点F叫抛物线的焦点,
直线l叫抛物线的准线.|MF|=dd抛物线的定义:抛物线的标准方程思考:抛物线是轴对称图形吗?l解:以过F且垂直于l的直线为x轴,垂足为K.以FK的中点O为坐标原点建立直角坐标系xoy.两边平方,整理得M(x,y)F依题意得这就是所求的轨迹方程.1.建立坐标系2.设动点坐标,相关点的坐标.3.列方程4.化简,整理5.证明(略)抛物线的标准方程 把方程y2=2px(p>0)叫做抛物线的标准方程.其中p为正常数,表示焦点在x轴正半轴上. p的几何意义是:焦点坐标是准线方程为:焦点到准线的距离抛物线的标准方程P的意义:抛物线的焦点到准线的距离四种抛物线的对比方程的特点:(1)左边是二次式(2)右边是一次式,(3)一次项的系数
的正负决定了开
口方向.决定了焦点的位
置.如何判断抛物线的焦点位置,开口方向?⑴一次项的变量如为x(或y),则焦点就在x轴(或y轴)上; ⑵一次项的系数的正负决定了开口方向。例1:求下列抛物线的焦点坐标和准线方程:
⑴y2 =6x
⑵y2 =-6x
⑶y=6x2注:求抛物线的焦点一定要先把抛物线化为标准形式,后定焦点、开口及准线.⑴焦点坐标是F(0,-2);⑵准线方程为x = 1;⑹过点A(-3,2).x2 =-8yy2 =-4x例2.根据下列条件,求抛物线的标准方程.⑶焦点在x轴上,焦点到准线的距离为2;⑷焦点到准线的距离为2;⑸焦点在直线3x-4y-12=0上y2=±4xy2=±4x或x2=±4yy2=16x或x2=-12y⑺焦点在x轴上,抛物线上的点M(-3,m)到焦点的距离等于5.y2 =12xy2 =xy2 =±4x、x2 =±4y练2.求下列抛物线的焦点坐标和准线方程:
(1)y2 = 20x (2)x2= y
(3)2y2 +5x =0 (4)x2 +8y =0(5,0)x=-5(0,-2)y=2例3.若直线l:y=kx-2与抛物线y2=8x交于A、B两点,且AB中点的横坐标为2,求此直线l的方程.②以①中的弦为底边,以x轴上的点P为顶点作三角形,当三角形的面积为9时,求点P坐标.
