山东省新泰市龙廷镇中心学校2015-2016学年九年级下学期第一次月考数学试题(附答案)
文档属性
| 名称 | 山东省新泰市龙廷镇中心学校2015-2016学年九年级下学期第一次月考数学试题(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 377.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-17 23:13:19 | ||
图片预览



文档简介
初中数学
一.选择题(共20小题)
1.(2015 日照)的算术平方根是( )
A.2 B.±2 C. D.±
2.(2015 宜宾)把代数式3x3﹣12x2+12x分解因式,结果正确的是( )
A.3x(x2﹣4x+4) B.3x(x﹣4)2 C.3x(x+2)(x﹣2) D.3x(x﹣2)2
3.(2015 宁夏)生物学家发现了一种病毒的长度约为0.00000432毫米.数据0.00000432用科学记数法表示为( )
A.0.432×10﹣5 B.4.32×10﹣6 C.4.32×10﹣7 D.43.2×10﹣7
4.(2015 绵阳)若+|2a﹣b+1|=0,则(b﹣a)2015=( )
A.﹣1 B.1 C.52015 D.﹣52015
5.(2015 广州)已知a,b满足方程组,则a+b的值为( )
A.﹣4 B.4 C.﹣2 D.2
6.(2015 营口)若关于x的分式方程+=2有增根,则m的值是( )
A.m=﹣1 B.m=0 C.m=3 D.m=0或m=3
7.(2014 德阳)已知方程﹣a=,且关于x的不等式组只有4个整数解,那么b的取值范围是( )
A.﹣1<b≤3 B.2<b≤3 C.8≤b<9 D.3≤b<4
8.(2015 潍坊)若式子+(k﹣1)0有意义,则一次函数y=(k﹣1)x+1﹣k的图象可能是( )
A. B. C. D.
9.(2015 贺州)已知k1<0<k2,则函数y=和y=k2x﹣1的图象大致是( )
A.B. C. D
10.(2015 宁夏)函数y=与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是( )
A. B. C. D.
11.(2015 南宁)一个正多边形的内角和为540°,则这个正多边形的每一个外角等于( )
A.60° B.72° C.90° D.108°
12.(2015 潍坊)将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯内径(图中小圆的直径)是8cm,水的最大深度是2cm,则杯底有水部分的面积是( )
A.(π﹣4)cm2 B.(π﹣8)cm2 C.(π﹣4)cm2 D.(π﹣2)cm2
13.(2015 枣庄)如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,边B1C1与CD交于点O,则四边形AB1OD的面积是( )
A. B. C. D.﹣1
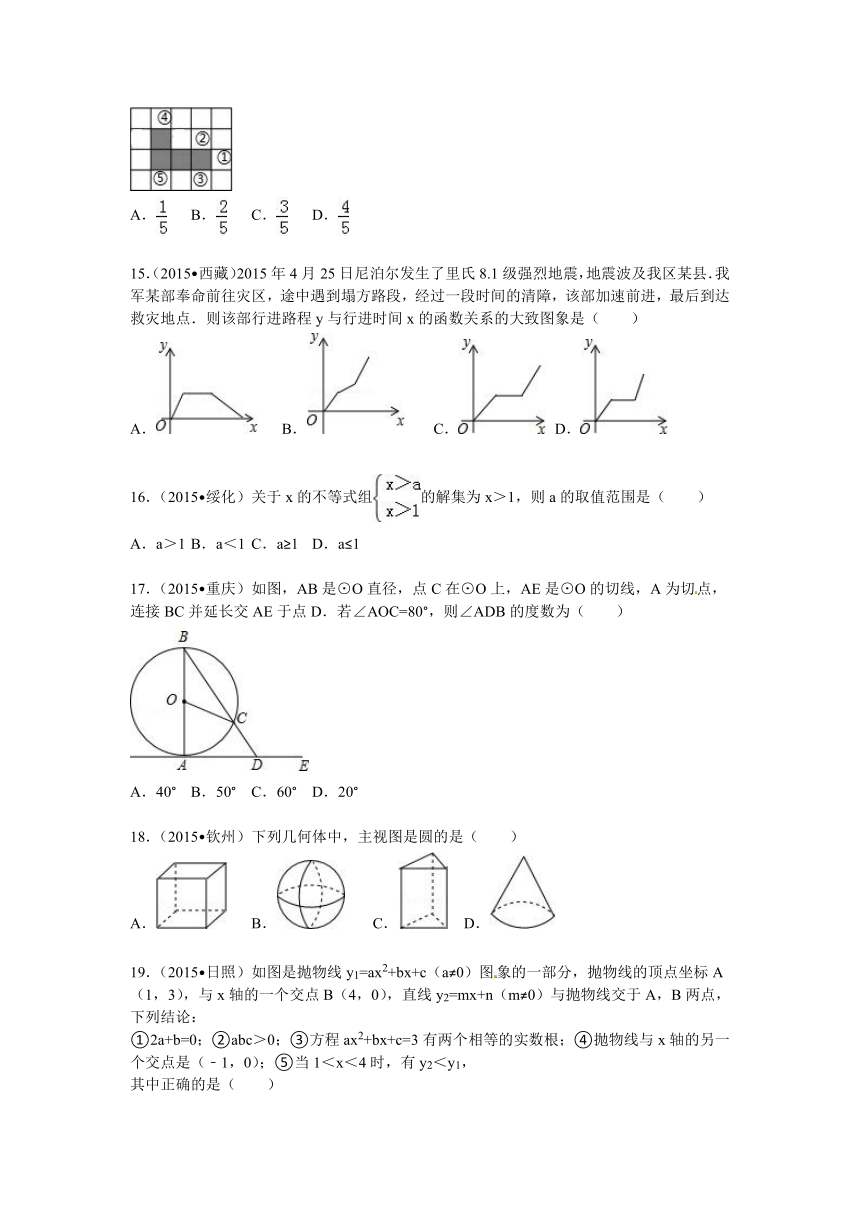
14.(2015 泰安)如图,在方格纸中,随机选择标有序号①②③④⑤中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的概率是( )
A. B. C. D.
15.(2015 西藏)2015年4月25日尼泊尔发生了里氏8.1级强烈地震,地震波及我区某县.我军某部奉命前往灾区,途中遇到塌方路段,经过一段时间的清障,该部加速前进,最后到达救灾地点.则该部行进路程y与行进时间x的函数关系的大致图象是( )
A. B. C. D.
16.(2015 绥化)关于x的不等式组的解集为x>1,则a的取值范围是( )
A.a>1 B.a<1 C.a≥1 D.a≤1
17.(2015 重庆)如图,AB是⊙O直径,点C在⊙O上,AE是⊙O的切线,A为切点,连接BC并延长交AE于点D.若∠AOC=80°,则∠ADB的度数为( )
A.40° B.50° C.60° D.20°
18.(2015 钦州)下列几何体中,主视图是圆的是( )
A. B. C. D.
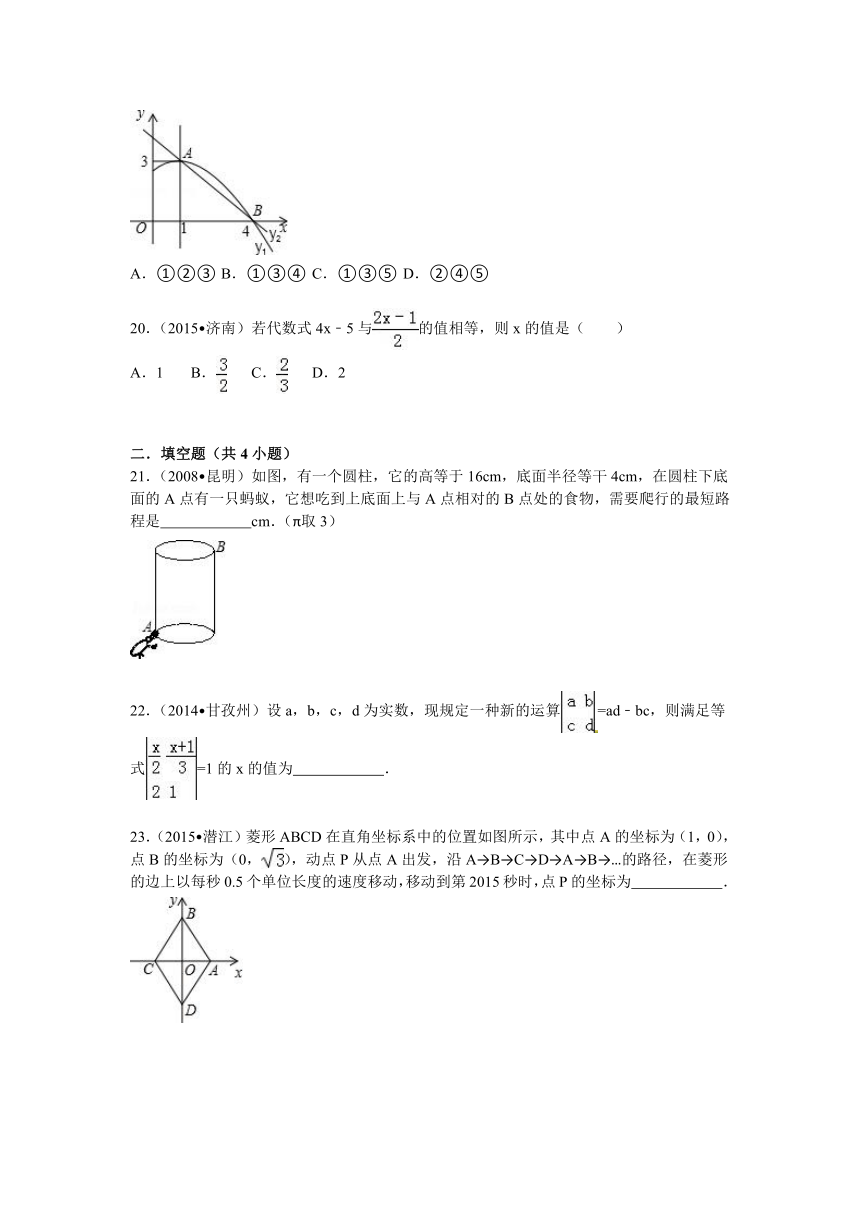
19.(2015 日照)如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:
①2a+b=0;②abc>0;③方程ax2+bx+c=3有两个相等的实数根;④抛物线与x轴的另一个交点是(﹣1,0);⑤当1<x<4时,有y2<y1,
其中正确的是( )
A.①②③ B.①③④ C.①③⑤ D.②④⑤
20.(2015 济南)若代数式4x﹣5与的值相等,则x的值是( )
A.1 B. C. D.2
二.填空题(共4小题)
21.(2008 昆明)如图,有一个圆柱,它的高等于16cm,底面半径等干4cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,需要爬行的最短路程是 cm.(π取3)
22.(2014 甘孜州)设a,b,c,d为实数,现规定一种新的运算=ad﹣bc,则满足等式=1的x的值为 .
23.(2015 潜江)菱形ABCD在直角坐标系中的位置如图所示,其中点A的坐标为(1,0),点B的坐标为(0,),动点P从点A出发,沿A→B→C→D→A→B→…的路径,在菱形的边上以每秒0.5个单位长度的速度移动,移动到第2015秒时,点P的坐标为 .
24.(2015 河南)如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交于点E,以点O为圆心,OC的长为半径作交OB于点D.若OA=2,则阴影部分的面积为 .
三.解答题(共5小题)
25.(2015 湖州)某工厂计划在规定时间内生产24000个零件.若每天比原计划多生产30个零件,则在规定时间内可以多生产300个零件.
(1)求原计划每天生产的零件个数和规定的天数;
(2)为了提前完成生产任务,工厂在安排原有工人按原计划正常生产的同时,引进5组机器人生产流水线共同参与零件生产,已知每组机器人生产流水线每天生产零件的个数比20个工人原计划每天生产的零件总数还多20%.按此测算,恰好提前两天完成24000个零件的生产任务,求原计划安排的工人人数.
26.(2015 娄底)“为了安全,请勿超速”.如图,一条公路建成通车,在某直线路段MN限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.(参考数据:≈1.41,≈1.73)
27.(2015 临沂)如图1,在正方形ABCD的外侧,作两个等边三角形ADE和DCF,连接AF,BE.
(1)请判断:AF与BE的数量关系是 ,位置关系是 ;
(2)如图2,若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF,且EA=ED=FD=FC”,第(1)问中的结论是否仍然成立?请作出判断并给予说明;
(3)若三角形ADE和DCF为一般三角形,且AE=DF,ED=FC,第(1)问中的结论都能成立吗?请直接写出你的判断.
28.(2015 内江)如图,抛物线与x轴交于点A(﹣,0)、点B(2,0),与y轴交于点C(0,1),连接BC.
(1)求抛物线的函数关系式;
(2)点N为抛物线上的一个动点,过点N作NP⊥x轴于点P,设点N的横坐标为t(﹣<t<2),求△ABN的面积S与t的函数关系式;
(3)若﹣<t<2且t≠0时△OPN∽△COB,求点N的坐标.
29.(2015 苏州)如图,已知AD是△ABC的角平分线,⊙O经过A、B、D三点.过点B作BE∥AD,交⊙O于点E,连接ED
(1)求证:ED∥AC;
(2)若BD=2CD,设△EBD的面积为S1,△ADC的面积为S2,且S12﹣16S2+4=0,求△ABC的面积.
试卷答案
1-5 CDBAB 6-10 ADACB 11-15 BADCD 16-20 DBBCB
21. 20 22. -10 23. (,﹣) 24. +
25解:(1)设原计划每天生产的零件x个,依题意有
=,
解得x=2400,
经检验,x=2400是原方程的根,且符合题意.
∴规定的天数为24000÷2400=10(天).
答:原计划每天生产的零件2400个,规定的天数是10天;
(2)设原计划安排的工人人数为y人,依题意有
[5×20×(1+20%)×+2400]×(10﹣2)=24000,
解得y=480,
经检验,y=480是原方程的根,且符合题意.
答:原计划安排的工人人数为480人.
26.解:此车没有超速.
理由:过C作CH⊥MN,
∵∠CBN=60°,BC=200米,
∴CH=BC sin60°=200×=100(米),
BH=BC cos60°=100(米),
∵∠CAN=45°,
∴AH=CH=100米,
∴AB=100﹣100≈73(m),
∵60千米/小时=m/s,
∴=14.6(m/s)<≈16.7(m/s),
∴此车没有超速.
27解:(1)AF与BE的数量关系是:AF=BE,位置关系是:AF⊥BE.
(2)结论仍然成立.
理由是:∵正方形ABCD中,AB=AD=CD,
∴在△ADE和△DCF中,,
∴△ADE≌△DCF,
∴∠DAE=∠CDF,
又∵正方形ABCD中,∠BAD=∠ADC=90°,
∴∠BAE=∠ADF,
∴在△ABE和△ADF中,,
∴△ABE≌△ADF,
∴BE=AF,∠ABM=∠DAF,
又∵∠DAF+∠BAM=90°,
∴∠ABM+∠BAM=90°,
∴在△ABM中,∠AMB=180°﹣(∠ABM+∠BAM)=90°,
∴BE⊥AF;
(3)第(1)问中的结论都能成立.
理由是:∵正方形ABCD中,AB=AD=CD,
∴在△ADE和△DCF中,,
∴△ADE≌△DCF,
∴∠DAE=∠CDF,
又∵正方形ABCD中,∠BAD=∠ADC=90°,
∴∠BAE=∠ADF,
∴在△ABE和△ADF中,,
∴△ABE≌△ADF,
∴BE=AF,∠ABM=∠DAF,
又∵∠DAF+∠BAM=90°,
∴∠ABM+∠BAM=90°,
∴在△ABM中,∠AMB=180°﹣(∠ABM+∠BAM)=90°,
28.解:(1)设抛物线的解析式为y=ax2+bx+c,由题可得:
,
解得:,
∴抛物线的函数关系式为y=﹣x2+x+1;
(2)当﹣<t<2时,yN>0,
∴NP=|yN|=yN=﹣t2+t+1,
∴S=AB PN
=×(2+)×(﹣t2+t+1)
=(﹣t2+t+1)
=﹣t2+t+;
(3)∵△OPN∽△COB,
∴=,
∴=,
∴PN=2PO.
①当﹣<t<0时,PN==yN=﹣t2+t+1,PO==﹣t,
∴﹣t2+t+1=﹣2t,
整理得:3t2﹣9t﹣2=0,
解得:t1=,t2=.
∵>0,﹣<<0,
∴t=,此时点N的坐标为(,);
②当0<t<2时,PN==yN=﹣t2+t+1,PO==t,
∴﹣t2+t+1=2t,
整理得:3t2﹣t﹣2=0,
解得:t3=﹣,t4=1.
∵﹣<0,0<1<2,
∴t=1,此时点N的坐标为(1,2).
综上所述:点N的坐标为(,)或(1,2).
29.(1)证明:∵AD是△ABC的角平分线,
∴∠BAD=∠DAC,
∵∠E=∠BAD,
∴∠E=∠DAC,
∵BE∥AD,
∴∠E=∠EDA,
∴∠EDA=∠DAC,
∴ED∥AC;
(2)解:∵BE∥AD,
∴∠EBD=∠ADC,
∵∠E=∠DAC,
∴△EBD∽△ADC,且相似比k=,
∴=k2=4,即s1=4s2,
∵﹣16S2+4=0,
∴16﹣16S2+4=0,
即=0,
∴S2=,
∵====3,
∴S△ABC=.
一.选择题(共20小题)
1.(2015 日照)的算术平方根是( )
A.2 B.±2 C. D.±
2.(2015 宜宾)把代数式3x3﹣12x2+12x分解因式,结果正确的是( )
A.3x(x2﹣4x+4) B.3x(x﹣4)2 C.3x(x+2)(x﹣2) D.3x(x﹣2)2
3.(2015 宁夏)生物学家发现了一种病毒的长度约为0.00000432毫米.数据0.00000432用科学记数法表示为( )
A.0.432×10﹣5 B.4.32×10﹣6 C.4.32×10﹣7 D.43.2×10﹣7
4.(2015 绵阳)若+|2a﹣b+1|=0,则(b﹣a)2015=( )
A.﹣1 B.1 C.52015 D.﹣52015
5.(2015 广州)已知a,b满足方程组,则a+b的值为( )
A.﹣4 B.4 C.﹣2 D.2
6.(2015 营口)若关于x的分式方程+=2有增根,则m的值是( )
A.m=﹣1 B.m=0 C.m=3 D.m=0或m=3
7.(2014 德阳)已知方程﹣a=,且关于x的不等式组只有4个整数解,那么b的取值范围是( )
A.﹣1<b≤3 B.2<b≤3 C.8≤b<9 D.3≤b<4
8.(2015 潍坊)若式子+(k﹣1)0有意义,则一次函数y=(k﹣1)x+1﹣k的图象可能是( )
A. B. C. D.
9.(2015 贺州)已知k1<0<k2,则函数y=和y=k2x﹣1的图象大致是( )
A.B. C. D
10.(2015 宁夏)函数y=与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是( )
A. B. C. D.
11.(2015 南宁)一个正多边形的内角和为540°,则这个正多边形的每一个外角等于( )
A.60° B.72° C.90° D.108°
12.(2015 潍坊)将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯内径(图中小圆的直径)是8cm,水的最大深度是2cm,则杯底有水部分的面积是( )
A.(π﹣4)cm2 B.(π﹣8)cm2 C.(π﹣4)cm2 D.(π﹣2)cm2
13.(2015 枣庄)如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,边B1C1与CD交于点O,则四边形AB1OD的面积是( )
A. B. C. D.﹣1
14.(2015 泰安)如图,在方格纸中,随机选择标有序号①②③④⑤中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的概率是( )
A. B. C. D.
15.(2015 西藏)2015年4月25日尼泊尔发生了里氏8.1级强烈地震,地震波及我区某县.我军某部奉命前往灾区,途中遇到塌方路段,经过一段时间的清障,该部加速前进,最后到达救灾地点.则该部行进路程y与行进时间x的函数关系的大致图象是( )
A. B. C. D.
16.(2015 绥化)关于x的不等式组的解集为x>1,则a的取值范围是( )
A.a>1 B.a<1 C.a≥1 D.a≤1
17.(2015 重庆)如图,AB是⊙O直径,点C在⊙O上,AE是⊙O的切线,A为切点,连接BC并延长交AE于点D.若∠AOC=80°,则∠ADB的度数为( )
A.40° B.50° C.60° D.20°
18.(2015 钦州)下列几何体中,主视图是圆的是( )
A. B. C. D.
19.(2015 日照)如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:
①2a+b=0;②abc>0;③方程ax2+bx+c=3有两个相等的实数根;④抛物线与x轴的另一个交点是(﹣1,0);⑤当1<x<4时,有y2<y1,
其中正确的是( )
A.①②③ B.①③④ C.①③⑤ D.②④⑤
20.(2015 济南)若代数式4x﹣5与的值相等,则x的值是( )
A.1 B. C. D.2
二.填空题(共4小题)
21.(2008 昆明)如图,有一个圆柱,它的高等于16cm,底面半径等干4cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,需要爬行的最短路程是 cm.(π取3)
22.(2014 甘孜州)设a,b,c,d为实数,现规定一种新的运算=ad﹣bc,则满足等式=1的x的值为 .
23.(2015 潜江)菱形ABCD在直角坐标系中的位置如图所示,其中点A的坐标为(1,0),点B的坐标为(0,),动点P从点A出发,沿A→B→C→D→A→B→…的路径,在菱形的边上以每秒0.5个单位长度的速度移动,移动到第2015秒时,点P的坐标为 .
24.(2015 河南)如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交于点E,以点O为圆心,OC的长为半径作交OB于点D.若OA=2,则阴影部分的面积为 .
三.解答题(共5小题)
25.(2015 湖州)某工厂计划在规定时间内生产24000个零件.若每天比原计划多生产30个零件,则在规定时间内可以多生产300个零件.
(1)求原计划每天生产的零件个数和规定的天数;
(2)为了提前完成生产任务,工厂在安排原有工人按原计划正常生产的同时,引进5组机器人生产流水线共同参与零件生产,已知每组机器人生产流水线每天生产零件的个数比20个工人原计划每天生产的零件总数还多20%.按此测算,恰好提前两天完成24000个零件的生产任务,求原计划安排的工人人数.
26.(2015 娄底)“为了安全,请勿超速”.如图,一条公路建成通车,在某直线路段MN限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.(参考数据:≈1.41,≈1.73)
27.(2015 临沂)如图1,在正方形ABCD的外侧,作两个等边三角形ADE和DCF,连接AF,BE.
(1)请判断:AF与BE的数量关系是 ,位置关系是 ;
(2)如图2,若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF,且EA=ED=FD=FC”,第(1)问中的结论是否仍然成立?请作出判断并给予说明;
(3)若三角形ADE和DCF为一般三角形,且AE=DF,ED=FC,第(1)问中的结论都能成立吗?请直接写出你的判断.
28.(2015 内江)如图,抛物线与x轴交于点A(﹣,0)、点B(2,0),与y轴交于点C(0,1),连接BC.
(1)求抛物线的函数关系式;
(2)点N为抛物线上的一个动点,过点N作NP⊥x轴于点P,设点N的横坐标为t(﹣<t<2),求△ABN的面积S与t的函数关系式;
(3)若﹣<t<2且t≠0时△OPN∽△COB,求点N的坐标.
29.(2015 苏州)如图,已知AD是△ABC的角平分线,⊙O经过A、B、D三点.过点B作BE∥AD,交⊙O于点E,连接ED
(1)求证:ED∥AC;
(2)若BD=2CD,设△EBD的面积为S1,△ADC的面积为S2,且S12﹣16S2+4=0,求△ABC的面积.
试卷答案
1-5 CDBAB 6-10 ADACB 11-15 BADCD 16-20 DBBCB
21. 20 22. -10 23. (,﹣) 24. +
25解:(1)设原计划每天生产的零件x个,依题意有
=,
解得x=2400,
经检验,x=2400是原方程的根,且符合题意.
∴规定的天数为24000÷2400=10(天).
答:原计划每天生产的零件2400个,规定的天数是10天;
(2)设原计划安排的工人人数为y人,依题意有
[5×20×(1+20%)×+2400]×(10﹣2)=24000,
解得y=480,
经检验,y=480是原方程的根,且符合题意.
答:原计划安排的工人人数为480人.
26.解:此车没有超速.
理由:过C作CH⊥MN,
∵∠CBN=60°,BC=200米,
∴CH=BC sin60°=200×=100(米),
BH=BC cos60°=100(米),
∵∠CAN=45°,
∴AH=CH=100米,
∴AB=100﹣100≈73(m),
∵60千米/小时=m/s,
∴=14.6(m/s)<≈16.7(m/s),
∴此车没有超速.
27解:(1)AF与BE的数量关系是:AF=BE,位置关系是:AF⊥BE.
(2)结论仍然成立.
理由是:∵正方形ABCD中,AB=AD=CD,
∴在△ADE和△DCF中,,
∴△ADE≌△DCF,
∴∠DAE=∠CDF,
又∵正方形ABCD中,∠BAD=∠ADC=90°,
∴∠BAE=∠ADF,
∴在△ABE和△ADF中,,
∴△ABE≌△ADF,
∴BE=AF,∠ABM=∠DAF,
又∵∠DAF+∠BAM=90°,
∴∠ABM+∠BAM=90°,
∴在△ABM中,∠AMB=180°﹣(∠ABM+∠BAM)=90°,
∴BE⊥AF;
(3)第(1)问中的结论都能成立.
理由是:∵正方形ABCD中,AB=AD=CD,
∴在△ADE和△DCF中,,
∴△ADE≌△DCF,
∴∠DAE=∠CDF,
又∵正方形ABCD中,∠BAD=∠ADC=90°,
∴∠BAE=∠ADF,
∴在△ABE和△ADF中,,
∴△ABE≌△ADF,
∴BE=AF,∠ABM=∠DAF,
又∵∠DAF+∠BAM=90°,
∴∠ABM+∠BAM=90°,
∴在△ABM中,∠AMB=180°﹣(∠ABM+∠BAM)=90°,
28.解:(1)设抛物线的解析式为y=ax2+bx+c,由题可得:
,
解得:,
∴抛物线的函数关系式为y=﹣x2+x+1;
(2)当﹣<t<2时,yN>0,
∴NP=|yN|=yN=﹣t2+t+1,
∴S=AB PN
=×(2+)×(﹣t2+t+1)
=(﹣t2+t+1)
=﹣t2+t+;
(3)∵△OPN∽△COB,
∴=,
∴=,
∴PN=2PO.
①当﹣<t<0时,PN==yN=﹣t2+t+1,PO==﹣t,
∴﹣t2+t+1=﹣2t,
整理得:3t2﹣9t﹣2=0,
解得:t1=,t2=.
∵>0,﹣<<0,
∴t=,此时点N的坐标为(,);
②当0<t<2时,PN==yN=﹣t2+t+1,PO==t,
∴﹣t2+t+1=2t,
整理得:3t2﹣t﹣2=0,
解得:t3=﹣,t4=1.
∵﹣<0,0<1<2,
∴t=1,此时点N的坐标为(1,2).
综上所述:点N的坐标为(,)或(1,2).
29.(1)证明:∵AD是△ABC的角平分线,
∴∠BAD=∠DAC,
∵∠E=∠BAD,
∴∠E=∠DAC,
∵BE∥AD,
∴∠E=∠EDA,
∴∠EDA=∠DAC,
∴ED∥AC;
(2)解:∵BE∥AD,
∴∠EBD=∠ADC,
∵∠E=∠DAC,
∴△EBD∽△ADC,且相似比k=,
∴=k2=4,即s1=4s2,
∵﹣16S2+4=0,
∴16﹣16S2+4=0,
即=0,
∴S2=,
∵====3,
∴S△ABC=.
同课章节目录
