人教A版 数学必修第二册 8.6.3 平面与平面垂直 课件(共30张PPT)
文档属性
| 名称 | 人教A版 数学必修第二册 8.6.3 平面与平面垂直 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-13 14:03:21 | ||
图片预览






文档简介
(共30张PPT)
平面与平面垂直
第 一 课 时
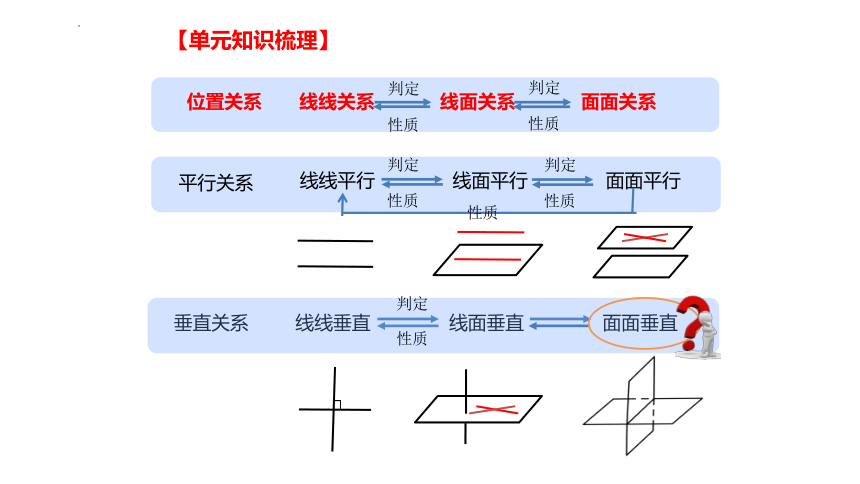
【单元知识梳理】
垂直关系
线线垂直
线面垂直
面面垂直
线线关系
线面关系
面面关系
位置关系
判定
性质
判定
性质
判定
性质
平行关系
线线平行
线面平行
面面平行
判定
性质
判定
性质
性质
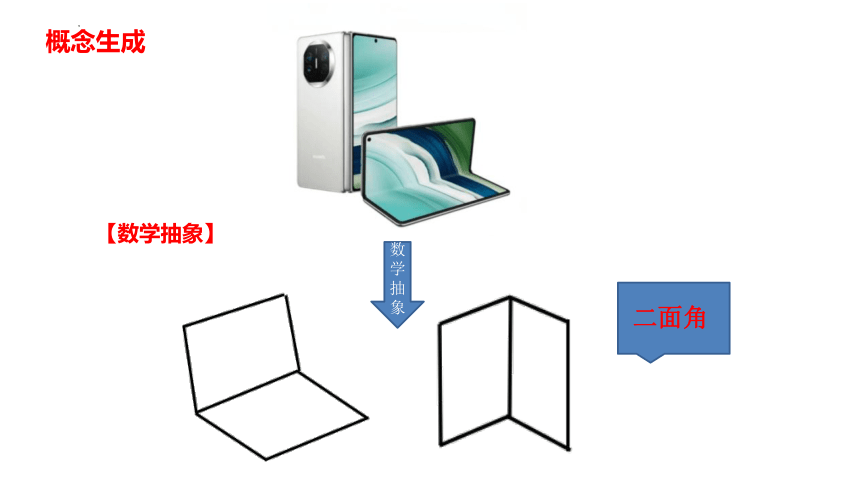
【问题1】观察两幅折叠手机图片,你能从中观察到点、线、面中的哪些几何元素?
二面角
数学抽象
概念生成
【数学抽象】
类 比
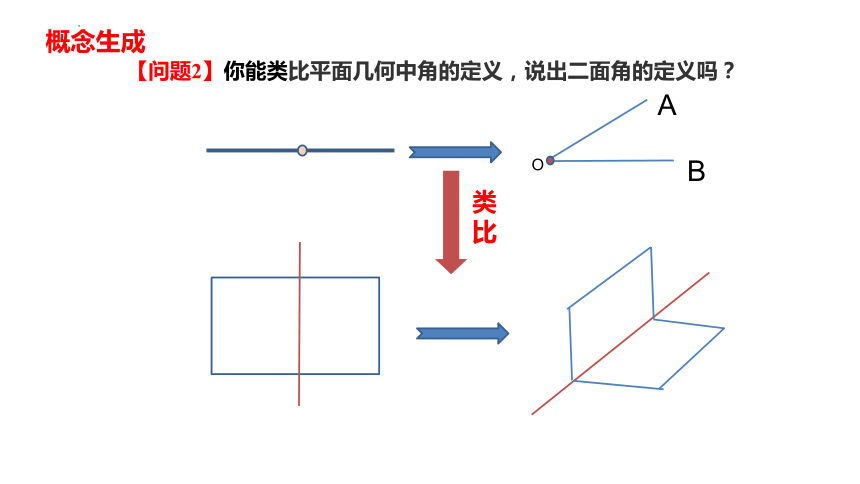
【问题2】你能类比平面几何中角的定义,说出二面角的定义吗?
O
A
B
概念生成
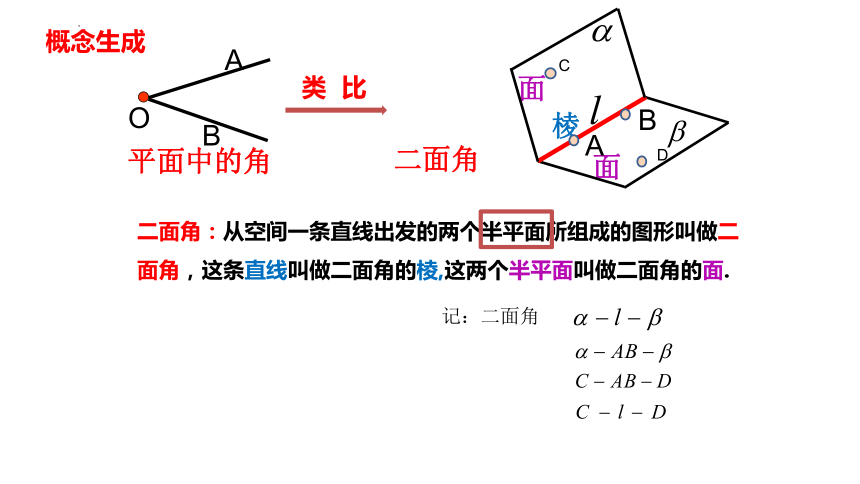
二面角:从空间一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫做二面角的棱,这两个半平面叫做二面角的面.
棱
面
面
二面角
O
平面中的角
类 比
A
B
A
B
C
D
概念生成
折叠手机在打开的过程中,会给人以面面“夹角”变大的感觉,说明二面角是有大小的,如何来度量二面角的大小?
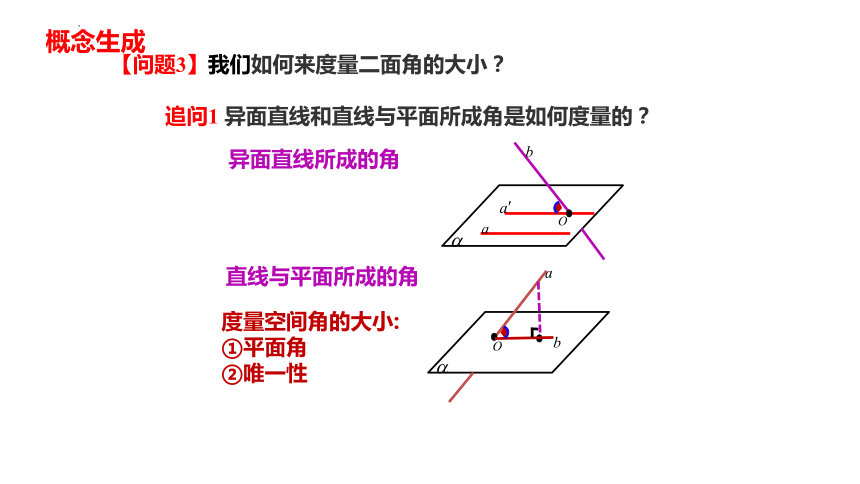
【问题3】我们如何来度量二面角的大小?
概念生成
异面直线所成的角
直线与平面所成的角
度量空间角的大小:
①平面角
②唯一性
【问题3】我们如何来度量二面角的大小?
追问1 异面直线和直线与平面所成角是如何度量的?
概念生成
【问题3】我们如何来度量二面角的大小?
大家动手折一折!
概念生成
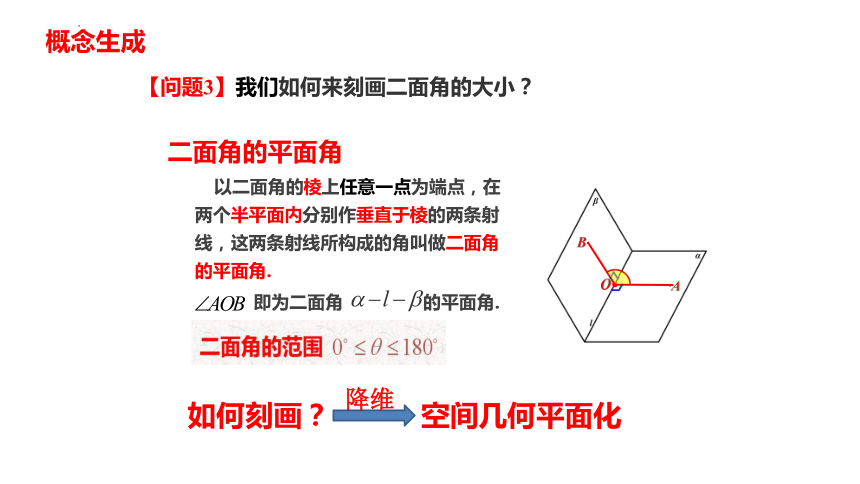
【问题3】我们如何来刻画二面角的大小?
【追问2】 如何使画出的平面角能跟随二面角的变化而变化?
大家动手画一画!画出平面角
概念生成
概念生成
【问题3】我们如何来刻画二面角的大小?
小组讨论:
将二面角的半平面绕着棱旋转,在二面角的大小变化过程中,观察画出的平面角随之变化的趋势,总结出你认为合理的理由。
以二面角的棱上任意一点为端点,在两个半平面内分别作垂直于棱的两条射线,这两条射线所构成的角叫做二面角的平面角.
即为二面角 的平面角.
空间几何平面化
如何刻画?
【问题3】我们如何来刻画二面角的大小?
降维
概念生成
二面角的平面角
【结论】二面角的大小用它的平面角的大小来度量,即二面角的大小具有唯一性( 等角定理:如果一个角的两边和另
一个角的两边分别平行,并且方向相同,那么这两个角相等。)
【问题3】大家讨论一下,如何理解定义中在二面角棱上任取一点?
深化定义
①顶点在棱上;
②两边分别在两个面内;
③边都要垂直于二面角的棱.
二面角的平面角必须满足
二面角的平面角大小与顶点在棱上的位置无关,只与二面角的张角大小有关.
平面角大小的唯一性
二面角的范围
当两个半平面重合时,规定
当两个半平面合成平面时,
规定
二面角的平面角
直二面角
平面角是直角的二面角叫做直二面角
深化定义
类 比
【问题4】你能类比平面几何两条直线夹角,说出平面与平面夹角的特点吗?
定义是判定面面垂直的方法之一.
一般的,如果两个平面α与β所成角的大小为则称这两个平面互相垂直,记作
平面与平面垂直的定义
直二面角
观察正方体,回答如下问题:
(1)平面D1ABC1与DABC垂直吗?
(2)平面A1ABB1与DABC垂直吗?
B
A
C
D
A1
C1
D1
B1
观察正方体,回答如下问题:
(1)平面D1ABC1与DABC垂直吗?
(2)平面A1ABB1与DABC垂直吗?
【小试牛刀】
观察正方体,回答如下问题:
(1)平面D1ABC1与DABC垂直吗?
(2)平面A1ABB1与DABC垂直吗?
观察正方体,回答如下问题:
(1)平面D1ABC1与DABC垂直吗?
(2)平面A1ABB1与DABC垂直吗?
B
A
C
D
A1
C1
D1
B1
【小试牛刀】
【问题5】还有其他方法证明面面垂直吗?
追问1 旋转门在旋转过程中, 每一扇门是否与地面垂直?
追问2 凭你的直观感觉,这是为 什么呢?
【探究】平面与平面垂直的判定定理
【问题6】通过直观感觉,你能抽象出一个关于平面与平面垂直的数学命题吗?
命题:如果一个平面经过另外一个平面的 一条垂线, 则这两个平面互相垂直。
真假?
m
【问题7】你能证明这个命题的真假吗?小组合作,理论证明证一证!
【小组合作】
【问题7】你能证明这个命题的真假吗?
判定定理:如果一个平面经过另外一个平面的 一条垂线,则这两个平面互相垂直。
自然语言
符号语言
图形语言
简称:线面垂直,则面面垂直。
m
.已知A是ΔBCD所在平面外一点,AB=AD,
BC=CD,E是BD的中点,
求证:平面AEC⊥平面BCD
D
A
C
B
E
【例题】
小组讨论,你找到的垂线是哪条线,为什么?
.已知A是ΔBCD所在平面外一点,AB=AD,
BC=CD,E是BD的中点,
求证:平面AEC⊥平面BCD
D
A
C
B
E
证明:
【例题】
关键
找垂线
.如图,AB是☉O的直径, PA垂直于☉O所在
的平面,C是圆周上不同于A, B的任意一点.
求证:平面PAC⊥平面PBC.
【当堂检测】
证明:∵AB是☉O的直径,C是圆周上不同于A,B的任意一点,
∴∠ACB=90°,
∴BC⊥AC.
又∵PA⊥平面ABC,
BC 平面ABC,
∴PA⊥BC且
∴BC⊥平面PAC.
∵BC 平面PBC,
∴平面PBC⊥平面PAC.
你还能在图形中找出其他面面垂直吗?
鳖臑(biē nào):在我国三角锥体的古称。
四个面均为直角三角形的四面体。
《九章算术》
作者及成书年代不可考,刘徽为它做过注释
数学史
类比
直二面角
平面角
二面角
二面角的平面角
刻画
度量
特 殊
定 义
面面垂直
面面垂直的判定定理
归纳推理
抽象
【课堂小结】
平面与平面垂直
第 一 课 时
【单元知识梳理】
垂直关系
线线垂直
线面垂直
面面垂直
线线关系
线面关系
面面关系
位置关系
判定
性质
判定
性质
判定
性质
平行关系
线线平行
线面平行
面面平行
判定
性质
判定
性质
性质
【问题1】观察两幅折叠手机图片,你能从中观察到点、线、面中的哪些几何元素?
二面角
数学抽象
概念生成
【数学抽象】
类 比
【问题2】你能类比平面几何中角的定义,说出二面角的定义吗?
O
A
B
概念生成
二面角:从空间一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫做二面角的棱,这两个半平面叫做二面角的面.
棱
面
面
二面角
O
平面中的角
类 比
A
B
A
B
C
D
概念生成
折叠手机在打开的过程中,会给人以面面“夹角”变大的感觉,说明二面角是有大小的,如何来度量二面角的大小?
【问题3】我们如何来度量二面角的大小?
概念生成
异面直线所成的角
直线与平面所成的角
度量空间角的大小:
①平面角
②唯一性
【问题3】我们如何来度量二面角的大小?
追问1 异面直线和直线与平面所成角是如何度量的?
概念生成
【问题3】我们如何来度量二面角的大小?
大家动手折一折!
概念生成
【问题3】我们如何来刻画二面角的大小?
【追问2】 如何使画出的平面角能跟随二面角的变化而变化?
大家动手画一画!画出平面角
概念生成
概念生成
【问题3】我们如何来刻画二面角的大小?
小组讨论:
将二面角的半平面绕着棱旋转,在二面角的大小变化过程中,观察画出的平面角随之变化的趋势,总结出你认为合理的理由。
以二面角的棱上任意一点为端点,在两个半平面内分别作垂直于棱的两条射线,这两条射线所构成的角叫做二面角的平面角.
即为二面角 的平面角.
空间几何平面化
如何刻画?
【问题3】我们如何来刻画二面角的大小?
降维
概念生成
二面角的平面角
【结论】二面角的大小用它的平面角的大小来度量,即二面角的大小具有唯一性( 等角定理:如果一个角的两边和另
一个角的两边分别平行,并且方向相同,那么这两个角相等。)
【问题3】大家讨论一下,如何理解定义中在二面角棱上任取一点?
深化定义
①顶点在棱上;
②两边分别在两个面内;
③边都要垂直于二面角的棱.
二面角的平面角必须满足
二面角的平面角大小与顶点在棱上的位置无关,只与二面角的张角大小有关.
平面角大小的唯一性
二面角的范围
当两个半平面重合时,规定
当两个半平面合成平面时,
规定
二面角的平面角
直二面角
平面角是直角的二面角叫做直二面角
深化定义
类 比
【问题4】你能类比平面几何两条直线夹角,说出平面与平面夹角的特点吗?
定义是判定面面垂直的方法之一.
一般的,如果两个平面α与β所成角的大小为则称这两个平面互相垂直,记作
平面与平面垂直的定义
直二面角
观察正方体,回答如下问题:
(1)平面D1ABC1与DABC垂直吗?
(2)平面A1ABB1与DABC垂直吗?
B
A
C
D
A1
C1
D1
B1
观察正方体,回答如下问题:
(1)平面D1ABC1与DABC垂直吗?
(2)平面A1ABB1与DABC垂直吗?
【小试牛刀】
观察正方体,回答如下问题:
(1)平面D1ABC1与DABC垂直吗?
(2)平面A1ABB1与DABC垂直吗?
观察正方体,回答如下问题:
(1)平面D1ABC1与DABC垂直吗?
(2)平面A1ABB1与DABC垂直吗?
B
A
C
D
A1
C1
D1
B1
【小试牛刀】
【问题5】还有其他方法证明面面垂直吗?
追问1 旋转门在旋转过程中, 每一扇门是否与地面垂直?
追问2 凭你的直观感觉,这是为 什么呢?
【探究】平面与平面垂直的判定定理
【问题6】通过直观感觉,你能抽象出一个关于平面与平面垂直的数学命题吗?
命题:如果一个平面经过另外一个平面的 一条垂线, 则这两个平面互相垂直。
真假?
m
【问题7】你能证明这个命题的真假吗?小组合作,理论证明证一证!
【小组合作】
【问题7】你能证明这个命题的真假吗?
判定定理:如果一个平面经过另外一个平面的 一条垂线,则这两个平面互相垂直。
自然语言
符号语言
图形语言
简称:线面垂直,则面面垂直。
m
.已知A是ΔBCD所在平面外一点,AB=AD,
BC=CD,E是BD的中点,
求证:平面AEC⊥平面BCD
D
A
C
B
E
【例题】
小组讨论,你找到的垂线是哪条线,为什么?
.已知A是ΔBCD所在平面外一点,AB=AD,
BC=CD,E是BD的中点,
求证:平面AEC⊥平面BCD
D
A
C
B
E
证明:
【例题】
关键
找垂线
.如图,AB是☉O的直径, PA垂直于☉O所在
的平面,C是圆周上不同于A, B的任意一点.
求证:平面PAC⊥平面PBC.
【当堂检测】
证明:∵AB是☉O的直径,C是圆周上不同于A,B的任意一点,
∴∠ACB=90°,
∴BC⊥AC.
又∵PA⊥平面ABC,
BC 平面ABC,
∴PA⊥BC且
∴BC⊥平面PAC.
∵BC 平面PBC,
∴平面PBC⊥平面PAC.
你还能在图形中找出其他面面垂直吗?
鳖臑(biē nào):在我国三角锥体的古称。
四个面均为直角三角形的四面体。
《九章算术》
作者及成书年代不可考,刘徽为它做过注释
数学史
类比
直二面角
平面角
二面角
二面角的平面角
刻画
度量
特 殊
定 义
面面垂直
面面垂直的判定定理
归纳推理
抽象
【课堂小结】
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
