人教A版 选择性必修第一册 1.4.1空间中的点、直线、平面与空间向量 课件(共17张PPT)
文档属性
| 名称 | 人教A版 选择性必修第一册 1.4.1空间中的点、直线、平面与空间向量 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 38.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-13 14:04:13 | ||
图片预览




文档简介
(共17张PPT)
空间中的点、直线、平面
与空间向量
空间向量在立体几何中的应用
探究一 点与空间向量
探究一 点与空间向量
问题1:如图所示的四面体O-ABC中,棱OA,OB,OC的长度分别为3,2,2,怎样借助空间向量来描述A,B,C在空间中是不同的点?
问题2:一般地,怎样借助空间向量来刻画空间中某个点的位置?
空间向量在立体几何中的应用
一般地,如果在空间中指定一点O ,那么空间中任意一点P 的位置,都可以由向量 唯一确定,此时, 通常称为点P 的位置向量.
特别地,空间直角坐标系中的任意一点都由它的位置向量唯一确定,从而也就由它的坐标唯一确定.
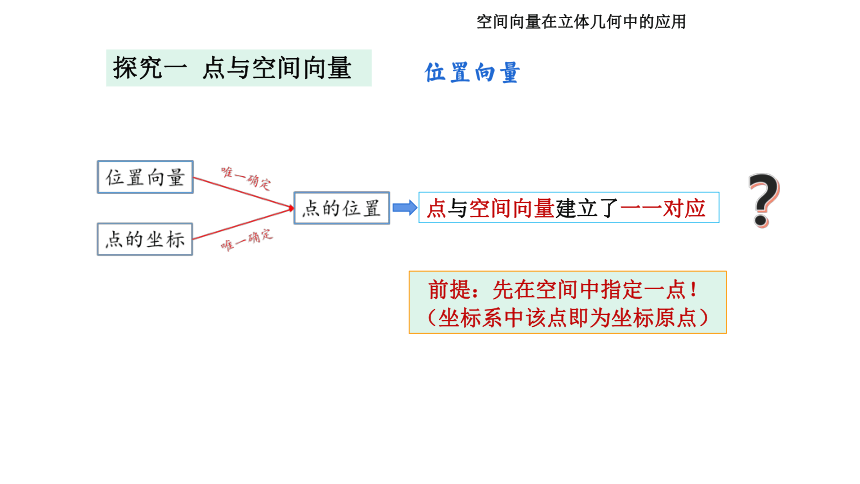
探究一 点与空间向量
位置向量
空间向量在立体几何中的应用
前提:先在空间中指定一点!
(坐标系中该点即为坐标原点)
?
空间向量在立体几何中的应用
点与空间向量建立了一一对应
探究一 点与空间向量
位置向量
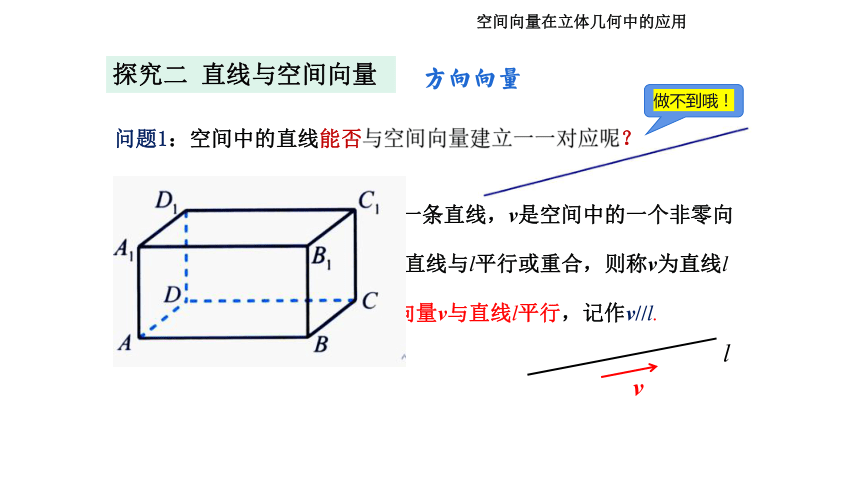
问题1:空间中的直线能否与空间向量建立一一对应呢?
一般地,如果l是空间中的一条直线,v是空间中的一个非零向量,且表示v的有向线段所在的直线与l平行或重合,则称v为直线l的一个方向向量,此时,也称向量v与直线l平行,记作v//l.
v
l
探究二 直线与空间向量
空间向量在立体几何中的应用
做不到哦!
方向向量
问题2:一条直线的方向向量有多少个呢?一个向量可能是多少条直线的方向向量呢?
探究二 直线与空间向量
空间向量在立体几何中的应用
结论:空间中的一个定点和一个方向向量可以确定一条直线的位置.
但不是一一对应哦!
小试牛刀
空间向量在立体几何中的应用
问题1:我们已经知,根据方向向量和一个点可以确定一条直线的位置,
那么,对于空间中的平面,能否引进类似的向量来刻画其位置呢?
探究三 平面与空间向量
空间向量在立体几何中的应用
问题2:请你用自己的话来说一说平面的法向量是如何定义的.
探究三 平面与空间向量
空间向量在立体几何中的应用
法向量
由此,你想到在空间直角坐标系中求解一个平面的法向量的方法了吗?
探究三 平面与空间向量
空间向量在立体几何中的应用
例2 如图所示,已知空间直角坐标系中的三棱锥O-ABC中,O(0,0,0),A(3,0,0),B(0,2,0),C(0,0,2),求平面ABC的一个法向量.
典例分析
空间向量在立体几何中的应用
例2 如图所示,已知空间直角坐标系中的三棱锥O-ABC中,O(0,0,0),A(3,0,0),B(0,2,0),C(0,0,2),求平面ABC的一个法向量.
典例分析
空间向量在立体几何中的应用
评测练习
如图所示,已知空间直角坐标系中的三棱锥O-ABC中,O(0,0,0),A(a,0,0),B(0,b,0),C(0,0,c),其中abc≠0,求平面ABC的一个法向量.
空间向量在立体几何中的应用
向量是一个强大的工具,
它为我们在代数与几何的世界中搭建了一座便捷的桥梁。
让我们使用好向量,在代数与几何中自由穿梭吧!
空间向量在立体几何中的应用
空间中的点、直线、平面
与空间向量
空间向量在立体几何中的应用
探究一 点与空间向量
探究一 点与空间向量
问题1:如图所示的四面体O-ABC中,棱OA,OB,OC的长度分别为3,2,2,怎样借助空间向量来描述A,B,C在空间中是不同的点?
问题2:一般地,怎样借助空间向量来刻画空间中某个点的位置?
空间向量在立体几何中的应用
一般地,如果在空间中指定一点O ,那么空间中任意一点P 的位置,都可以由向量 唯一确定,此时, 通常称为点P 的位置向量.
特别地,空间直角坐标系中的任意一点都由它的位置向量唯一确定,从而也就由它的坐标唯一确定.
探究一 点与空间向量
位置向量
空间向量在立体几何中的应用
前提:先在空间中指定一点!
(坐标系中该点即为坐标原点)
?
空间向量在立体几何中的应用
点与空间向量建立了一一对应
探究一 点与空间向量
位置向量
问题1:空间中的直线能否与空间向量建立一一对应呢?
一般地,如果l是空间中的一条直线,v是空间中的一个非零向量,且表示v的有向线段所在的直线与l平行或重合,则称v为直线l的一个方向向量,此时,也称向量v与直线l平行,记作v//l.
v
l
探究二 直线与空间向量
空间向量在立体几何中的应用
做不到哦!
方向向量
问题2:一条直线的方向向量有多少个呢?一个向量可能是多少条直线的方向向量呢?
探究二 直线与空间向量
空间向量在立体几何中的应用
结论:空间中的一个定点和一个方向向量可以确定一条直线的位置.
但不是一一对应哦!
小试牛刀
空间向量在立体几何中的应用
问题1:我们已经知,根据方向向量和一个点可以确定一条直线的位置,
那么,对于空间中的平面,能否引进类似的向量来刻画其位置呢?
探究三 平面与空间向量
空间向量在立体几何中的应用
问题2:请你用自己的话来说一说平面的法向量是如何定义的.
探究三 平面与空间向量
空间向量在立体几何中的应用
法向量
由此,你想到在空间直角坐标系中求解一个平面的法向量的方法了吗?
探究三 平面与空间向量
空间向量在立体几何中的应用
例2 如图所示,已知空间直角坐标系中的三棱锥O-ABC中,O(0,0,0),A(3,0,0),B(0,2,0),C(0,0,2),求平面ABC的一个法向量.
典例分析
空间向量在立体几何中的应用
例2 如图所示,已知空间直角坐标系中的三棱锥O-ABC中,O(0,0,0),A(3,0,0),B(0,2,0),C(0,0,2),求平面ABC的一个法向量.
典例分析
空间向量在立体几何中的应用
评测练习
如图所示,已知空间直角坐标系中的三棱锥O-ABC中,O(0,0,0),A(a,0,0),B(0,b,0),C(0,0,c),其中abc≠0,求平面ABC的一个法向量.
空间向量在立体几何中的应用
向量是一个强大的工具,
它为我们在代数与几何的世界中搭建了一座便捷的桥梁。
让我们使用好向量,在代数与几何中自由穿梭吧!
空间向量在立体几何中的应用
