2024-2025学年青岛版(六三学制)六年级数学上册期末押题卷(含答案+解析)
文档属性
| 名称 | 2024-2025学年青岛版(六三学制)六年级数学上册期末押题卷(含答案+解析) |  | |
| 格式 | docx | ||
| 文件大小 | 416.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-11 12:45:25 | ||
图片预览



文档简介
保密★启用前
20224-2025学年六年级上册期末押题卷青岛版(六三学制)
数学
考试范围:六上全册 考试时间:100分钟
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择
1.下面三句话,错误的一句是( )。
A.假分数的倒数一定是真分数
B.1既不是质数也不是合数
C.0既不是正数也不是负数。
2.用一块地的种白菜,种青菜,剩下的地与种( )的地一样多。
A.白菜 B.青菜 C.白菜和青菜的总和
3.一项工程,甲队单独做要 15 天,乙队 4 天完成了这项工程的,丙队 3 天完成了工 程的,( )的工作效率最高。
A.甲队 B.乙队
C.丙队 D.三队效率一样高
4.奇奇卖拼图玩具,他有两种拼图玩具,原价相同,A种拼图先涨价35%,再降价30%;B 种拼图先降价35%,再涨价30%,A、B两种拼图玩具现价相比,( )。
A.A的高 B.B的高 C.同样高
5.要把∶化成最简整数比,比的前项和后项可以同时乘( )。
A.12和15的最大公因数 B.5和1的最小公倍数
C.12和15的最小公倍数 D.除0以外的相同数
6.如下图正方形的面积是10平方厘米,阴影部分的面积是( )
A.2.15cm2 B.7.85cm2 C.8.6cm2 D.2.56cm2
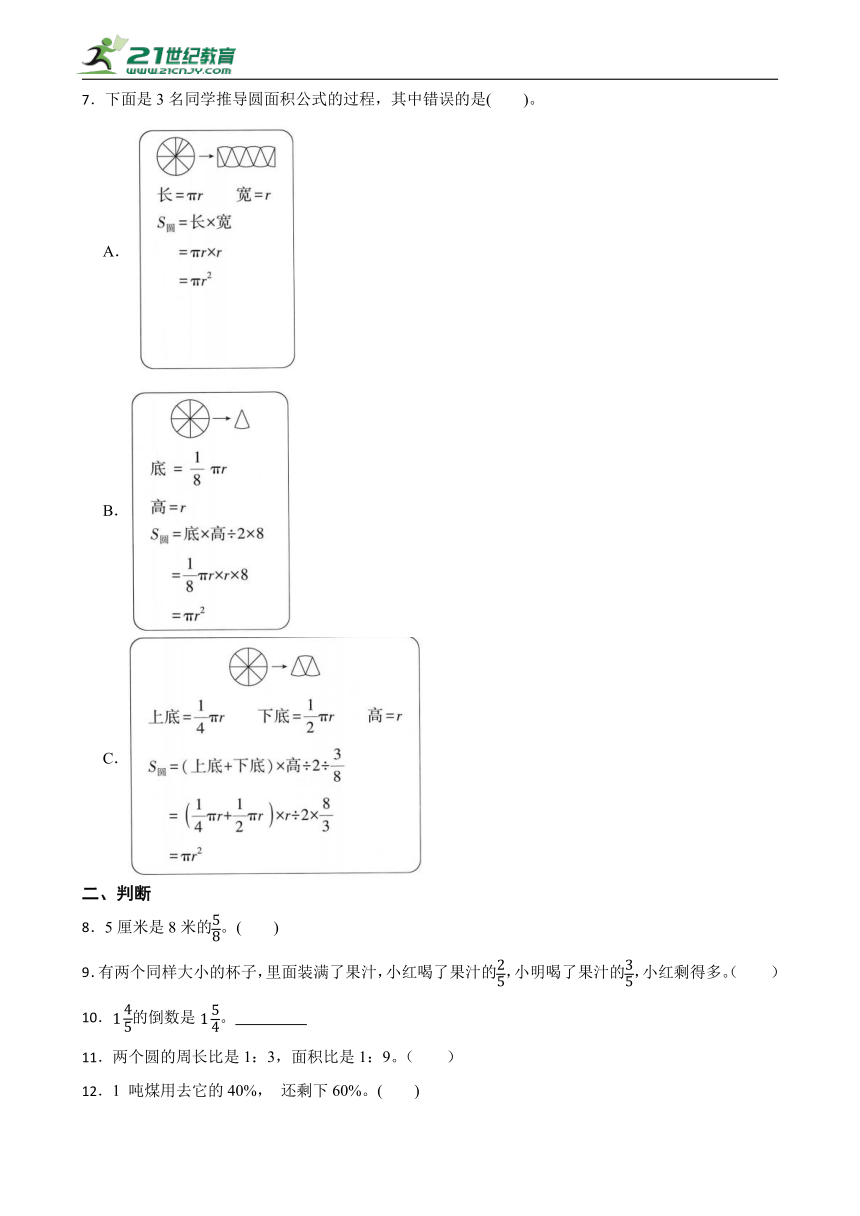
7.下面是3名同学推导圆面积公式的过程,其中错误的是( )。
A.
B.
C.
二、判断
8.5厘米是8米的。( )
9.有两个同样大小的杯子,里面装满了果汁,小红喝了果汁的,小明喝了果汁的,小红剩得多。( )
10.的倒数是。
11.两个圆的周长比是1:3,面积比是1:9。( )
12.1 吨煤用去它的40%, 还剩下60%。( )
13.圆心角是 120°的扇形面积一定大于圆心角是90°的扇形面积。( )
14.转动左边的转盘,转盘停止转动后,指针停在质数区域的可能性比停在合数区域的可能性大。( )
三、填空
15. 在里填上“>”“<”或“=”。
16.m和n互为倒数,= , 。
17.( P55第9题变式)点A的位置如图所示,则 的位置在 处, 的位置在 处。
18. 0.75= ÷4=9: = %
19.从甲堆货物中取出放入乙堆货物,这时两堆货物的重量相等,原来甲、乙两堆货物的比是 。
20.已知 %(M、N、L 均不为0),则M、N、L 这三个数的大小关系是 。
21.(几何直观)如下图,甲、乙两个三角形重叠部分的面积相当于甲三角形面积的,相当于乙三角形面积的,甲、乙两个三角形面积的最简整数比是 。
22.在12克的水中加入1克蜂蜜,蜂蜜与水的质量比是 : ,一辆汽车2个小时行驶了140千米,这辆车行驶的路程与时间的比值是 ,这个比值表示 。
23.一种大豆的出油率是30%,600 kg大豆可以榨油 kg;要榨450 kg的油,需要大豆 kg。
24.12个的和是 ; 吨的是 吨;
米比 米多米; 最小的合数的倒数是 。
25.2.4㎡增加 后是 ㎡, ㎡减少 后是2.4㎡。
26.“知野”科普探索小队的15名队员围成一个圆圈做活动总结,每相邻两名队员之间的距离都是0.8m。这个圆圈的周长是 m。
27.有这样一列数:2,5,11,23,47,…这列数的前6项的数之和为 。
28.3箱苹果和4箱梨共重120千克,已知每箱苹果比每箱梨重5千克。每箱苹果和每箱梨分别重多少千克?假设7箱全都是苹果,总质量比120千克重 千克;假设7箱全都是梨,总质量要比120千克轻 千克。
29.下图中大圆的直径是 cm,小圆的面积是 cm2。
四、计算
30.直接写出得数。
5.4÷10%=
31.解方程
x÷=12 ÷x=1-
32.简便运算
(1)24×( + - )
(2) ÷ ×
(3)0.34×12.5+66×0.125
五、解决问题
33.一笔奖金共1800元,现有两种分配方案可供选择。分配方案一:甲、乙、丙三人平均分;分配方案二:甲、乙、丙三人按2:3:5分配。将方案一改为方案二分配,谁将多得奖金? 多得多少元?
34.小林骑自行车去郊游,去时平均每小时行12千米, 小时到达。他原路返回时只用了 小时,返回时平均每小时行多少千米?
35. 为保证游客安全,某景区工作人员每天要花6时的时间上下山巡逻。上山巡逻的时间比下山巡逻的时间长。工作人员上山巡逻和下山巡逻的时间各是多长时间?(列方程解答)
36.某市普通出租车白天的收费标准如下:
①3km以内10元(包括3km);②超过3km的部分,每千米收费1.8元。
聪聪的爸爸早晨打车先送聪聪去学校再去公司上班。学校在家的正北方向公司在家的正南方向,家到学校的距离与家到公司的距离之比为3:5,聪聪的爸爸一共付了 24.4元的车费,则聪聪家距离学校和公司分别多远?(出租车行驶的路程为整千米数)
37.某款巧克力促销,妈妈买回了八盒巧克力,平均每盒巧克力的价格比原价便宜百分之多少
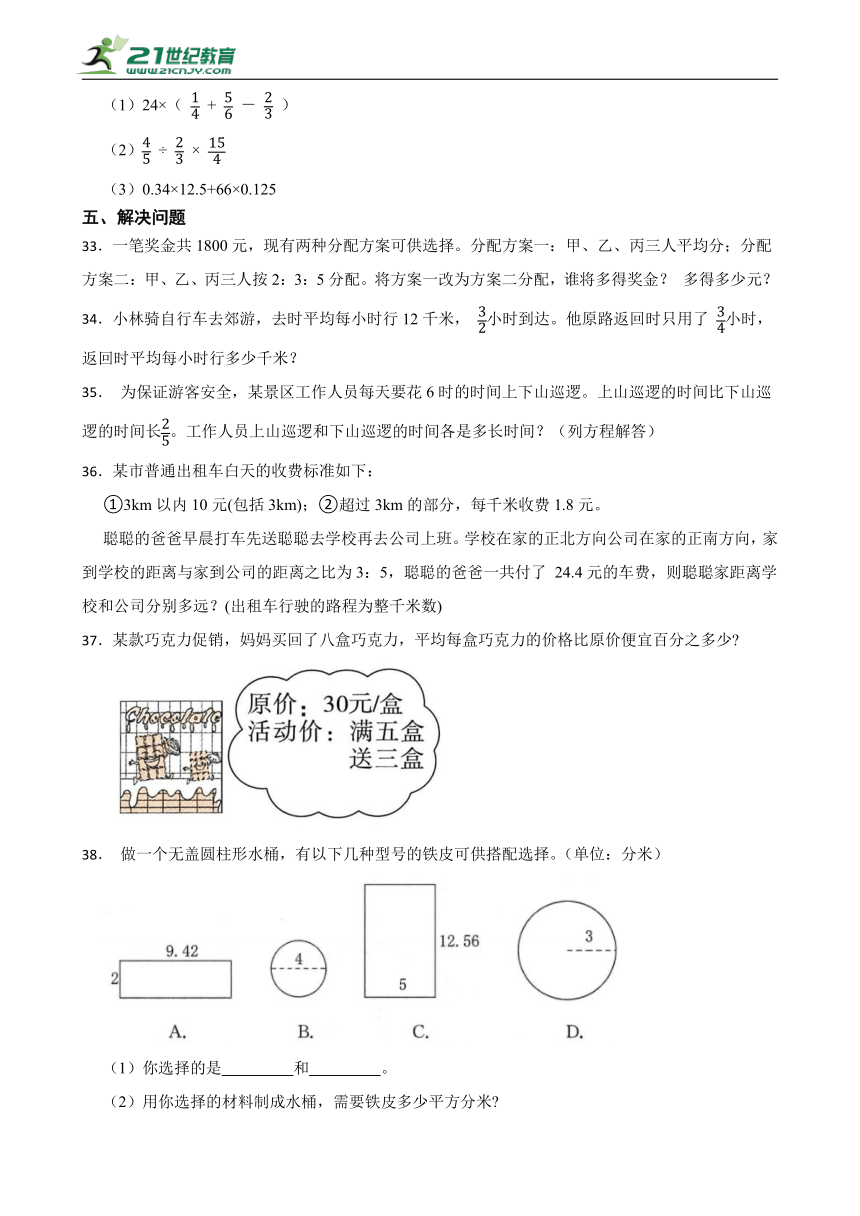
38. 做一个无盖圆柱形水桶,有以下几种型号的铁皮可供搭配选择。(单位:分米)
(1)你选择的是 和 。
(2)用你选择的材料制成水桶,需要铁皮多少平方分米
(3)用你选择的材料制成的水桶的容积是几升
39.如图,在梯形ABCD中,对角线AC,BD相交于O点,OE平行于AB. ,,求的面积。
40.甲、乙两车分别从A、B两地同时出发,相向而行,甲车和乙车行驶的速度比是4:5,相遇时距离两地中点32千米。A、B两地相距多少千米?
答案解析部分
1.A
解:假分数的倒数不一定是真分数,所以A项的话是错误的。
故答案为:A。
=1是假分数,但1的倒数还是1,所以假分数的倒数不一定是真分数;
1既不是合数也不是质数,最小的合数是4。
2.A
解:1--
=-
=
=,剩下的地与种白菜的地一样多。
故答案为:A。
剩下地占的分率=1-种白菜占的分率-种青菜占的分率,然后比较大小。
3.C
解:1÷15=
÷4=
÷3=
<<,丙队的工作效率最高。
故答案为:C。
工作效率=工作总量÷工作时间,然后比较大小。
4.A
解:设两种拼图玩具的原价都为1,
则A种拼图玩具的现价是(1+35%)×(1-30%)=0.945,
B种拼图玩具的现价是(1-35%)×(1+30%)=0.845,
0.945>0.845,
所以A的高;
故答案为:A。
设两种拼图玩具的原价都为1,A种拼图先涨价35%,价格即为原来的(1+35%),再降价30%后价格即为涨价后的(1-30%),B种拼图先降价35%,价格即为原来的(1-35%),再涨价30%,价格即为降价后的(1+30%),用乘法求解,再比较即可。
5.C
6.A
解:正方形的面积:(平方厘米)
圆的面积:(平方厘米)
圆的面积:(平方厘米)
阴影部分面积:10-7.85=2.15(平方厘米)
故答案为:A。
本题巧妙地利用正方形的面积恰好等于圆的半径的平方,在计算圆的面积时,直接代入使用,再根据阴影部分的面积=正方形的面积-圆的面积即可解答。
7.B
解:A选项将圆转化成长方形进行推导,推导过程和计算数据正确,该方法正确;
B选项将圆转化成扇形进而借助三角形的面积计算公式进行推导,推导过程思路正确,但是每个小三角形的底是,据此代入下面计算公式,也可以得出面积计算公式,该方法正确但是题干计算错误;
C选项将圆转化成梯形进行推导,推导过程和计算数据正确,该方法正确;
故答案为:B。
根据圆的周长计算公式:C=2πr,逐项长方形,三角形,梯形面积推导公式的正确性即可求解。
8.错误
解:8米=800厘米;;
故答案为:错误
首先,将8米转换成厘米,1米=100厘米,所以8米=800厘米。接下来,计算8米的,即厘米。然后,将计算结果500厘米与题目中给出的5厘米进行比较,可以明显看出,5厘米不是8米的。因此,题目中的说法是错误的。
9.正确
解:<,小红喝得少,则剩的多。
故答案为:正确。
有两个同样大小的杯子,里面装满了果汁,喝的少的剩下的多。
10.×
11.正确
解:假设两个圆的周长分别是2π和6π
小圆的半径=2π÷2÷π=1
大圆的半径=6π÷2÷π=3
小圆的面积=12×π=π
大圆的面积=32×π=9π
π:9π=1:9
因此,两个圆的周长比是1:3,面积比是1:9,原题说法正确。
故答案为:正确。
圆的周长=2πr,圆的面积=πr2;圆的半径比与周长比相等,面积比是半径的平方相比。
12.正确
解:剩下:1×(1-40%)=0.6(吨),0.6÷1×100%=60%;
故答案为:正确。
1吨煤用去40%,意味着用去了1吨的40%,也就是0.4吨;剩下的部分,也就是1吨减去0.4吨,等于0.6吨;而0.6吨占总量1吨的60%,因此,“还剩下60%”的说法是正确的。
13.错误
解:题干中没有告知圆的直径的具体面积,所以无法确定两个扇形面积的大小,所以原题说法错误。
故答案为:错误
计算扇形面积需要具体知道圆的半径,没有具体数值的情况下无法判断两个扇形面积的大小。
14.错误
解:1-10这几个数字中,质数有:2、3、5、7;合数有:4、6、8、9、10;
所以停在合数的可能性比质数的可能性大;
故答案为:错误。
把1-10这10个数字中的质数合数罗列出来,比较质数和合数的数量大小即可解答。
15.<,<,=,<
解:∵
∴<
∵
∴<
∵式子两边的两对因数的值分别相等
∴=
∵
∴<
故答案为:<,<,=,<。
一个数乘以一个小于一的数,结果小于这个数,根据这个规律,可以简便地判断两个式子结果的大小。
16.12;
解:如果m和n互为倒数,则m×n=1;
÷=×==12;
×==。
故答案为:12;。
互为倒数的两个数乘积是1,甲数除以乙数(0除外),等于甲数乘乙数的倒数,据此计算;
分数乘分数,能约分的先约分,然后用分子相乘的积作分子,分母相乘的积作分母,据此解答。
17.⑤;②
18.3;;75
解:0.75×4=3;9÷4=;0.75=75%。
故答案为:3;;75。
根据被除数=商×除数,用0.75乘4即可;根据比的后项=前项÷比值,用9除以0.75;将0.75的小数点向右移动两位,再添上%即可。
19.9∶5
20.M=N=L
解:因为 N×0.375,L×37.5%=L×0.375,所以M=N=L。
故答案为:M=N=L。
把除法转化成乘法,同时把分数、百分数都化成小数,这样就能判断三个字母表示数的大小。
21.9:25
解:甲三角形的面积×=乙三角形的面积×
甲:乙
=:
=9:25
故答案为:9:25。
根据题意可得:甲三角形的面积×=乙三角形的面积×,根据比例的基本性质,可得:甲:乙=:=9:25。据此解答。
22.1;12;70;这辆车的行驶速度
解:蜂蜜与水的质量比是1:12。140千米/2小时=70千米/小时。这个比值实际上代表的是汽车的平均速度。
故答案为:1;12;70;这辆车的行驶速度
本题考查的是比例和比值的概念及其应用。在第一部分,需要计算蜂蜜与水的质量比。在第二部分,需要计算汽车行驶的路程与时间的比值,以及这个比值代表的物理意义。
23.180;1500
解:600×30%=180(千克)
450÷30%=1500(千克)
故答案为:180;1500。
根据出油率=油的重量÷大豆的重量×100%,所以油的重量=大豆的重量×出油率,大豆的重量=油的重量÷出油率,据此解答。
24.10;;;
解:第一题:12×=10;
第二题:×=(吨);
第三题:-=(米);
第四题:最小的合数的倒数是。
故答案为:10;;;。
第一题:根据分数乘整数的意义求出12个的和;
第二题:求一个数的几分之几是多少,用乘法计算;
第三题:一只一个数比另一个数多多少,求另一个数用减法计算;
第四题:最小的合数是4,乘积是1的两个数互为倒数,根据倒数的意义判断4的倒数。
25.3;3.2
解:2.4×(1+)
=2.4×
=3(m2)
2.4÷(1-)
=2.4÷
=3.2(m2)
故答案为:3;3.2。
求一个数增加几分之几是多少,把原数看作单位“1”,原数×(1+增加的分率)=新数;
已知比一个数少几分之几是多少,要求这个数,用除法计算。
26.12
解:12×0.8=12m
故答案为:12
一共15人,每两人间隔0.8m,所以总长度是12米
27.183
:数列的规律是从第二个数起,前一个数的2倍加1等于后一个数。
前六项的和为:2+5+11+23+47+95=183
故答案为:186。
数列的规律是:从第二个数起,前一个数的2倍加1等于后一个数。然后把这6个数相加。
28.20;15
解:(120+20)÷7
=140÷7
=20(千克)
(120-15)÷7
=105÷7
=15(千克)
故答案为:20;15。
每箱苹果比每箱梨重5千克 , 假设7箱全都是苹果 ,则总质量为(120+20)=140(千克),那么总质量比120千克重140-120=20(千克); 假设7箱全都是梨,则总质量为(120-15)=105(千克),那么总质量比120千克轻120-105=15(千克)。
29.16;50.24
解:由图得大圆的直径为:2×8=16
小圆的半径=8÷2=4
小圆的面积S=πr2=π×=50.24
故答案为:16;50.24
由图知大圆半径=小圆直径,进而可以得到大圆直径=2×大圆半径,小圆半径=小圆直径÷2,再根据圆的面积S=πr2即可求出小圆面积。
30.
5.4÷10%=54
分数乘整数时,用分数的分子和整数相乘的积做分子,分母不变, 能约分的要先约分;
分数乘分数时,用分子相乘的积做分子,分母相乘的积做分母,能约分的先约分;
除数是分数的除法,先将除法变为乘法,再按分数乘法计算;
计算含百分数的式子时,可先将百分数转化为小数或分数再计算;
分数乘小数,可将小数与分母约分,再与分子相乘;
比的前项除以后项为比值。
31.
x÷=12
解:x=12×
x=3
x=3÷
x= ÷x=1-
解:÷x=
x=÷
x=
等式的基本性质1:等式两边同时加上(或减去)同一个整式,等式仍然成立;等式的基本性质2:等式两边同时乘或除以同一个不为0的整式,等式仍然成立;
第一题:根据等式的性质2,等式两边先同时乘以,再同时除以。
第二题:先计算出等号右边的结果,然后根据除数等于被除数除以商解答。
32.(1)解:24×( + - )
=24× +24× -24×
=6+20-16
=10
(2)解: ÷ ×
=× ×
=
(3)解:0.34×12.5+66×0.125
=0.34×12.5+0.66×12.5
=(0.34+0.66)×12.5
=1×12.5
=12.5
(1)一个数乘几个数的和与差,等于这个数分别同这几个数相乘,再把积相加或相减,结果不变。据此简算;
(2)先把除以化为乘,再三个分数一起,先约分,后计算;
(3)两个数相乘,一个因数扩大多少倍,另一个因数就相应的缩小多少倍,积不变,据此把66×0.125化为0.66×12.5;再按照乘法分配律进行简算。
33.解:方案一:1800÷3=600(元)
方案二:甲: ,1800×=360(元)
乙: ,×1800=540(元)
丙: ,×1800=900(元)
900>600, 900-600=300(元)
答:丙多得奖金,多得300元。
分配方案一,甲、乙、丙每人分得1800元的 ,每人分600元;
分配方案二,分得的钱数=1800元×对应的分率,据此解答。
34.解:12×÷
=18÷
=24(千米)
答:返回时平均每小时行24千米。
返回时的速度=去时的速度×去时用的时间÷返回用的时间。
35.解:设工作人员下山巡逻的时间为x时
=6
x=2.5
6-2.5=3.5(时)
答:工作人员上山巡逻的时间为3.5时,下山巡逻的时间为 2.5 时。
36.解:因为车费24.4元>10元,所以路程大于3 km,
(24.4-10) ÷1.8+3
=8+3
=11(km),
则聪聪家与学校间的距离为 (km),
聪聪家与公司间的距离为 (km);
答:聪聪家距离学校3km,距离公司5 km。
因为车费24.4元>10元,所以可以判断出路程大于3 km,用24.4-10可以得到超出过3km的部分的收费,除以单价即可得到超过3km的部分的路程,再加上3km即为出租车行驶的全程,因为出租车先去了学校然后折返去公司,可以得到出租车走了2个家到学校的距离+1个家到公司的距离,整个路程可以看作3+3+5=11份,家到学校的距离占3份,家到公司的距离占5份,据此求解。
37.解:30×(8-3)=150(元)
150÷8=18.75(元)
(30-18.75)÷30×100%=37.5%
答:平均每盒巧克力的价格比原价便宜37.5%
由于促销活动,妈妈实际只需要支付五盒巧克力的费用。每盒巧克力的原价是30元,求实际支付总额,妈妈总共得到了八盒巧克力,但只支付了150元,所以平均每盒巧克力的实际支付价格为 元。原价是30元,现在平均每盒的价格下降到了18.75元。价格下降的绝对值为 元。所以即可得出答案。
38.(1)B;C
(2)解:12.56×5+3.14×(4÷2)2
=62.8+12.56
=75.36(平方分米);
答:需要铁皮75.36平方分米。
(3)解:3.14×(4÷2)2×5
=3.14×20
=62.8(立方米)
=62.8(升);
答:水桶的容积是62.8升。
解:(1)9.42÷3.14=3(分米),
12.56÷3.14=4(分米),
只有BC组合符合条件;
故答案为:B;C。
(1)圆柱形水桶由一个圆形底面和一个侧面组成,侧面展开后是一个长方形,其长等于底面圆的周长宽等于水桶的高,所以圆的直径与侧面长方形的长要一致,据此选择;
(2)需要铁皮=长方形侧面积+圆的面积即可;
(3)水桶的容积计算公式为V=πr2h,据此求解。
39.解:如图所示,延长EO到AD,交AD于点F,
因为,AB//DC,所以,,
所以,OE=OF
可得,S△AOF=S△AOE,S△DOF=S△DOE;
S△ADE=S△AFE+S△DEF=2S△AOE+2S△DOE=100cm2
设OE交AD于点F,由AB//DC,可得,进而得出:OE=OF,由此,可得S△AOF=S△AOE,S△DOF=S△DOE,从而可得:S△ADE=S△AFE+S△DEF,代入数据即可求解
40.解:32×2÷(5-4)×(4+5)
=64÷1×9
=576(千米)
答:A、B两地相距576千米。
相遇时甲车和乙车行驶的路程比=相遇时甲车和乙车行驶的速度比=4:5。又因为两车相遇时距离两地中点 32千米,所以乙车比甲车多行驶的路程=32×2=64千米,乙车比甲车多行驶的份数=5-4=1份,先用除法计算出每份是多少千米,再用每份的千米数乘总份数。
20224-2025学年六年级上册期末押题卷青岛版(六三学制)
数学
考试范围:六上全册 考试时间:100分钟
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择
1.下面三句话,错误的一句是( )。
A.假分数的倒数一定是真分数
B.1既不是质数也不是合数
C.0既不是正数也不是负数。
2.用一块地的种白菜,种青菜,剩下的地与种( )的地一样多。
A.白菜 B.青菜 C.白菜和青菜的总和
3.一项工程,甲队单独做要 15 天,乙队 4 天完成了这项工程的,丙队 3 天完成了工 程的,( )的工作效率最高。
A.甲队 B.乙队
C.丙队 D.三队效率一样高
4.奇奇卖拼图玩具,他有两种拼图玩具,原价相同,A种拼图先涨价35%,再降价30%;B 种拼图先降价35%,再涨价30%,A、B两种拼图玩具现价相比,( )。
A.A的高 B.B的高 C.同样高
5.要把∶化成最简整数比,比的前项和后项可以同时乘( )。
A.12和15的最大公因数 B.5和1的最小公倍数
C.12和15的最小公倍数 D.除0以外的相同数
6.如下图正方形的面积是10平方厘米,阴影部分的面积是( )
A.2.15cm2 B.7.85cm2 C.8.6cm2 D.2.56cm2
7.下面是3名同学推导圆面积公式的过程,其中错误的是( )。
A.
B.
C.
二、判断
8.5厘米是8米的。( )
9.有两个同样大小的杯子,里面装满了果汁,小红喝了果汁的,小明喝了果汁的,小红剩得多。( )
10.的倒数是。
11.两个圆的周长比是1:3,面积比是1:9。( )
12.1 吨煤用去它的40%, 还剩下60%。( )
13.圆心角是 120°的扇形面积一定大于圆心角是90°的扇形面积。( )
14.转动左边的转盘,转盘停止转动后,指针停在质数区域的可能性比停在合数区域的可能性大。( )
三、填空
15. 在里填上“>”“<”或“=”。
16.m和n互为倒数,= , 。
17.( P55第9题变式)点A的位置如图所示,则 的位置在 处, 的位置在 处。
18. 0.75= ÷4=9: = %
19.从甲堆货物中取出放入乙堆货物,这时两堆货物的重量相等,原来甲、乙两堆货物的比是 。
20.已知 %(M、N、L 均不为0),则M、N、L 这三个数的大小关系是 。
21.(几何直观)如下图,甲、乙两个三角形重叠部分的面积相当于甲三角形面积的,相当于乙三角形面积的,甲、乙两个三角形面积的最简整数比是 。
22.在12克的水中加入1克蜂蜜,蜂蜜与水的质量比是 : ,一辆汽车2个小时行驶了140千米,这辆车行驶的路程与时间的比值是 ,这个比值表示 。
23.一种大豆的出油率是30%,600 kg大豆可以榨油 kg;要榨450 kg的油,需要大豆 kg。
24.12个的和是 ; 吨的是 吨;
米比 米多米; 最小的合数的倒数是 。
25.2.4㎡增加 后是 ㎡, ㎡减少 后是2.4㎡。
26.“知野”科普探索小队的15名队员围成一个圆圈做活动总结,每相邻两名队员之间的距离都是0.8m。这个圆圈的周长是 m。
27.有这样一列数:2,5,11,23,47,…这列数的前6项的数之和为 。
28.3箱苹果和4箱梨共重120千克,已知每箱苹果比每箱梨重5千克。每箱苹果和每箱梨分别重多少千克?假设7箱全都是苹果,总质量比120千克重 千克;假设7箱全都是梨,总质量要比120千克轻 千克。
29.下图中大圆的直径是 cm,小圆的面积是 cm2。
四、计算
30.直接写出得数。
5.4÷10%=
31.解方程
x÷=12 ÷x=1-
32.简便运算
(1)24×( + - )
(2) ÷ ×
(3)0.34×12.5+66×0.125
五、解决问题
33.一笔奖金共1800元,现有两种分配方案可供选择。分配方案一:甲、乙、丙三人平均分;分配方案二:甲、乙、丙三人按2:3:5分配。将方案一改为方案二分配,谁将多得奖金? 多得多少元?
34.小林骑自行车去郊游,去时平均每小时行12千米, 小时到达。他原路返回时只用了 小时,返回时平均每小时行多少千米?
35. 为保证游客安全,某景区工作人员每天要花6时的时间上下山巡逻。上山巡逻的时间比下山巡逻的时间长。工作人员上山巡逻和下山巡逻的时间各是多长时间?(列方程解答)
36.某市普通出租车白天的收费标准如下:
①3km以内10元(包括3km);②超过3km的部分,每千米收费1.8元。
聪聪的爸爸早晨打车先送聪聪去学校再去公司上班。学校在家的正北方向公司在家的正南方向,家到学校的距离与家到公司的距离之比为3:5,聪聪的爸爸一共付了 24.4元的车费,则聪聪家距离学校和公司分别多远?(出租车行驶的路程为整千米数)
37.某款巧克力促销,妈妈买回了八盒巧克力,平均每盒巧克力的价格比原价便宜百分之多少
38. 做一个无盖圆柱形水桶,有以下几种型号的铁皮可供搭配选择。(单位:分米)
(1)你选择的是 和 。
(2)用你选择的材料制成水桶,需要铁皮多少平方分米
(3)用你选择的材料制成的水桶的容积是几升
39.如图,在梯形ABCD中,对角线AC,BD相交于O点,OE平行于AB. ,,求的面积。
40.甲、乙两车分别从A、B两地同时出发,相向而行,甲车和乙车行驶的速度比是4:5,相遇时距离两地中点32千米。A、B两地相距多少千米?
答案解析部分
1.A
解:假分数的倒数不一定是真分数,所以A项的话是错误的。
故答案为:A。
=1是假分数,但1的倒数还是1,所以假分数的倒数不一定是真分数;
1既不是合数也不是质数,最小的合数是4。
2.A
解:1--
=-
=
=,剩下的地与种白菜的地一样多。
故答案为:A。
剩下地占的分率=1-种白菜占的分率-种青菜占的分率,然后比较大小。
3.C
解:1÷15=
÷4=
÷3=
<<,丙队的工作效率最高。
故答案为:C。
工作效率=工作总量÷工作时间,然后比较大小。
4.A
解:设两种拼图玩具的原价都为1,
则A种拼图玩具的现价是(1+35%)×(1-30%)=0.945,
B种拼图玩具的现价是(1-35%)×(1+30%)=0.845,
0.945>0.845,
所以A的高;
故答案为:A。
设两种拼图玩具的原价都为1,A种拼图先涨价35%,价格即为原来的(1+35%),再降价30%后价格即为涨价后的(1-30%),B种拼图先降价35%,价格即为原来的(1-35%),再涨价30%,价格即为降价后的(1+30%),用乘法求解,再比较即可。
5.C
6.A
解:正方形的面积:(平方厘米)
圆的面积:(平方厘米)
圆的面积:(平方厘米)
阴影部分面积:10-7.85=2.15(平方厘米)
故答案为:A。
本题巧妙地利用正方形的面积恰好等于圆的半径的平方,在计算圆的面积时,直接代入使用,再根据阴影部分的面积=正方形的面积-圆的面积即可解答。
7.B
解:A选项将圆转化成长方形进行推导,推导过程和计算数据正确,该方法正确;
B选项将圆转化成扇形进而借助三角形的面积计算公式进行推导,推导过程思路正确,但是每个小三角形的底是,据此代入下面计算公式,也可以得出面积计算公式,该方法正确但是题干计算错误;
C选项将圆转化成梯形进行推导,推导过程和计算数据正确,该方法正确;
故答案为:B。
根据圆的周长计算公式:C=2πr,逐项长方形,三角形,梯形面积推导公式的正确性即可求解。
8.错误
解:8米=800厘米;;
故答案为:错误
首先,将8米转换成厘米,1米=100厘米,所以8米=800厘米。接下来,计算8米的,即厘米。然后,将计算结果500厘米与题目中给出的5厘米进行比较,可以明显看出,5厘米不是8米的。因此,题目中的说法是错误的。
9.正确
解:<,小红喝得少,则剩的多。
故答案为:正确。
有两个同样大小的杯子,里面装满了果汁,喝的少的剩下的多。
10.×
11.正确
解:假设两个圆的周长分别是2π和6π
小圆的半径=2π÷2÷π=1
大圆的半径=6π÷2÷π=3
小圆的面积=12×π=π
大圆的面积=32×π=9π
π:9π=1:9
因此,两个圆的周长比是1:3,面积比是1:9,原题说法正确。
故答案为:正确。
圆的周长=2πr,圆的面积=πr2;圆的半径比与周长比相等,面积比是半径的平方相比。
12.正确
解:剩下:1×(1-40%)=0.6(吨),0.6÷1×100%=60%;
故答案为:正确。
1吨煤用去40%,意味着用去了1吨的40%,也就是0.4吨;剩下的部分,也就是1吨减去0.4吨,等于0.6吨;而0.6吨占总量1吨的60%,因此,“还剩下60%”的说法是正确的。
13.错误
解:题干中没有告知圆的直径的具体面积,所以无法确定两个扇形面积的大小,所以原题说法错误。
故答案为:错误
计算扇形面积需要具体知道圆的半径,没有具体数值的情况下无法判断两个扇形面积的大小。
14.错误
解:1-10这几个数字中,质数有:2、3、5、7;合数有:4、6、8、9、10;
所以停在合数的可能性比质数的可能性大;
故答案为:错误。
把1-10这10个数字中的质数合数罗列出来,比较质数和合数的数量大小即可解答。
15.<,<,=,<
解:∵
∴<
∵
∴<
∵式子两边的两对因数的值分别相等
∴=
∵
∴<
故答案为:<,<,=,<。
一个数乘以一个小于一的数,结果小于这个数,根据这个规律,可以简便地判断两个式子结果的大小。
16.12;
解:如果m和n互为倒数,则m×n=1;
÷=×==12;
×==。
故答案为:12;。
互为倒数的两个数乘积是1,甲数除以乙数(0除外),等于甲数乘乙数的倒数,据此计算;
分数乘分数,能约分的先约分,然后用分子相乘的积作分子,分母相乘的积作分母,据此解答。
17.⑤;②
18.3;;75
解:0.75×4=3;9÷4=;0.75=75%。
故答案为:3;;75。
根据被除数=商×除数,用0.75乘4即可;根据比的后项=前项÷比值,用9除以0.75;将0.75的小数点向右移动两位,再添上%即可。
19.9∶5
20.M=N=L
解:因为 N×0.375,L×37.5%=L×0.375,所以M=N=L。
故答案为:M=N=L。
把除法转化成乘法,同时把分数、百分数都化成小数,这样就能判断三个字母表示数的大小。
21.9:25
解:甲三角形的面积×=乙三角形的面积×
甲:乙
=:
=9:25
故答案为:9:25。
根据题意可得:甲三角形的面积×=乙三角形的面积×,根据比例的基本性质,可得:甲:乙=:=9:25。据此解答。
22.1;12;70;这辆车的行驶速度
解:蜂蜜与水的质量比是1:12。140千米/2小时=70千米/小时。这个比值实际上代表的是汽车的平均速度。
故答案为:1;12;70;这辆车的行驶速度
本题考查的是比例和比值的概念及其应用。在第一部分,需要计算蜂蜜与水的质量比。在第二部分,需要计算汽车行驶的路程与时间的比值,以及这个比值代表的物理意义。
23.180;1500
解:600×30%=180(千克)
450÷30%=1500(千克)
故答案为:180;1500。
根据出油率=油的重量÷大豆的重量×100%,所以油的重量=大豆的重量×出油率,大豆的重量=油的重量÷出油率,据此解答。
24.10;;;
解:第一题:12×=10;
第二题:×=(吨);
第三题:-=(米);
第四题:最小的合数的倒数是。
故答案为:10;;;。
第一题:根据分数乘整数的意义求出12个的和;
第二题:求一个数的几分之几是多少,用乘法计算;
第三题:一只一个数比另一个数多多少,求另一个数用减法计算;
第四题:最小的合数是4,乘积是1的两个数互为倒数,根据倒数的意义判断4的倒数。
25.3;3.2
解:2.4×(1+)
=2.4×
=3(m2)
2.4÷(1-)
=2.4÷
=3.2(m2)
故答案为:3;3.2。
求一个数增加几分之几是多少,把原数看作单位“1”,原数×(1+增加的分率)=新数;
已知比一个数少几分之几是多少,要求这个数,用除法计算。
26.12
解:12×0.8=12m
故答案为:12
一共15人,每两人间隔0.8m,所以总长度是12米
27.183
:数列的规律是从第二个数起,前一个数的2倍加1等于后一个数。
前六项的和为:2+5+11+23+47+95=183
故答案为:186。
数列的规律是:从第二个数起,前一个数的2倍加1等于后一个数。然后把这6个数相加。
28.20;15
解:(120+20)÷7
=140÷7
=20(千克)
(120-15)÷7
=105÷7
=15(千克)
故答案为:20;15。
每箱苹果比每箱梨重5千克 , 假设7箱全都是苹果 ,则总质量为(120+20)=140(千克),那么总质量比120千克重140-120=20(千克); 假设7箱全都是梨,则总质量为(120-15)=105(千克),那么总质量比120千克轻120-105=15(千克)。
29.16;50.24
解:由图得大圆的直径为:2×8=16
小圆的半径=8÷2=4
小圆的面积S=πr2=π×=50.24
故答案为:16;50.24
由图知大圆半径=小圆直径,进而可以得到大圆直径=2×大圆半径,小圆半径=小圆直径÷2,再根据圆的面积S=πr2即可求出小圆面积。
30.
5.4÷10%=54
分数乘整数时,用分数的分子和整数相乘的积做分子,分母不变, 能约分的要先约分;
分数乘分数时,用分子相乘的积做分子,分母相乘的积做分母,能约分的先约分;
除数是分数的除法,先将除法变为乘法,再按分数乘法计算;
计算含百分数的式子时,可先将百分数转化为小数或分数再计算;
分数乘小数,可将小数与分母约分,再与分子相乘;
比的前项除以后项为比值。
31.
x÷=12
解:x=12×
x=3
x=3÷
x= ÷x=1-
解:÷x=
x=÷
x=
等式的基本性质1:等式两边同时加上(或减去)同一个整式,等式仍然成立;等式的基本性质2:等式两边同时乘或除以同一个不为0的整式,等式仍然成立;
第一题:根据等式的性质2,等式两边先同时乘以,再同时除以。
第二题:先计算出等号右边的结果,然后根据除数等于被除数除以商解答。
32.(1)解:24×( + - )
=24× +24× -24×
=6+20-16
=10
(2)解: ÷ ×
=× ×
=
(3)解:0.34×12.5+66×0.125
=0.34×12.5+0.66×12.5
=(0.34+0.66)×12.5
=1×12.5
=12.5
(1)一个数乘几个数的和与差,等于这个数分别同这几个数相乘,再把积相加或相减,结果不变。据此简算;
(2)先把除以化为乘,再三个分数一起,先约分,后计算;
(3)两个数相乘,一个因数扩大多少倍,另一个因数就相应的缩小多少倍,积不变,据此把66×0.125化为0.66×12.5;再按照乘法分配律进行简算。
33.解:方案一:1800÷3=600(元)
方案二:甲: ,1800×=360(元)
乙: ,×1800=540(元)
丙: ,×1800=900(元)
900>600, 900-600=300(元)
答:丙多得奖金,多得300元。
分配方案一,甲、乙、丙每人分得1800元的 ,每人分600元;
分配方案二,分得的钱数=1800元×对应的分率,据此解答。
34.解:12×÷
=18÷
=24(千米)
答:返回时平均每小时行24千米。
返回时的速度=去时的速度×去时用的时间÷返回用的时间。
35.解:设工作人员下山巡逻的时间为x时
=6
x=2.5
6-2.5=3.5(时)
答:工作人员上山巡逻的时间为3.5时,下山巡逻的时间为 2.5 时。
36.解:因为车费24.4元>10元,所以路程大于3 km,
(24.4-10) ÷1.8+3
=8+3
=11(km),
则聪聪家与学校间的距离为 (km),
聪聪家与公司间的距离为 (km);
答:聪聪家距离学校3km,距离公司5 km。
因为车费24.4元>10元,所以可以判断出路程大于3 km,用24.4-10可以得到超出过3km的部分的收费,除以单价即可得到超过3km的部分的路程,再加上3km即为出租车行驶的全程,因为出租车先去了学校然后折返去公司,可以得到出租车走了2个家到学校的距离+1个家到公司的距离,整个路程可以看作3+3+5=11份,家到学校的距离占3份,家到公司的距离占5份,据此求解。
37.解:30×(8-3)=150(元)
150÷8=18.75(元)
(30-18.75)÷30×100%=37.5%
答:平均每盒巧克力的价格比原价便宜37.5%
由于促销活动,妈妈实际只需要支付五盒巧克力的费用。每盒巧克力的原价是30元,求实际支付总额,妈妈总共得到了八盒巧克力,但只支付了150元,所以平均每盒巧克力的实际支付价格为 元。原价是30元,现在平均每盒的价格下降到了18.75元。价格下降的绝对值为 元。所以即可得出答案。
38.(1)B;C
(2)解:12.56×5+3.14×(4÷2)2
=62.8+12.56
=75.36(平方分米);
答:需要铁皮75.36平方分米。
(3)解:3.14×(4÷2)2×5
=3.14×20
=62.8(立方米)
=62.8(升);
答:水桶的容积是62.8升。
解:(1)9.42÷3.14=3(分米),
12.56÷3.14=4(分米),
只有BC组合符合条件;
故答案为:B;C。
(1)圆柱形水桶由一个圆形底面和一个侧面组成,侧面展开后是一个长方形,其长等于底面圆的周长宽等于水桶的高,所以圆的直径与侧面长方形的长要一致,据此选择;
(2)需要铁皮=长方形侧面积+圆的面积即可;
(3)水桶的容积计算公式为V=πr2h,据此求解。
39.解:如图所示,延长EO到AD,交AD于点F,
因为,AB//DC,所以,,
所以,OE=OF
可得,S△AOF=S△AOE,S△DOF=S△DOE;
S△ADE=S△AFE+S△DEF=2S△AOE+2S△DOE=100cm2
设OE交AD于点F,由AB//DC,可得,进而得出:OE=OF,由此,可得S△AOF=S△AOE,S△DOF=S△DOE,从而可得:S△ADE=S△AFE+S△DEF,代入数据即可求解
40.解:32×2÷(5-4)×(4+5)
=64÷1×9
=576(千米)
答:A、B两地相距576千米。
相遇时甲车和乙车行驶的路程比=相遇时甲车和乙车行驶的速度比=4:5。又因为两车相遇时距离两地中点 32千米,所以乙车比甲车多行驶的路程=32×2=64千米,乙车比甲车多行驶的份数=5-4=1份,先用除法计算出每份是多少千米,再用每份的千米数乘总份数。
同课章节目录
