2.4.3向量与夹角 教案(表格式)2024-2025学年高二下学期数学湘教版(2019)选择性必修第二册
文档属性
| 名称 | 2.4.3向量与夹角 教案(表格式)2024-2025学年高二下学期数学湘教版(2019)选择性必修第二册 |

|
|
| 格式 | docx | ||
| 文件大小 | 693.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-12 00:00:00 | ||
图片预览

文档简介
课题名称:数学选择性必修第2册 向量与夹角
教学方法: “一体二化三导四学”教学模式和自主学习模式. (一体二化三导四学:以学生为主体,教学内容问题化,教学活动探究化,引导,指导,督导,自主学习,探究学习,合作学习,体验学习)
教学目标: 1.掌握异面直线、直线和平面,平面与平面所成的角的向量解法; 2.理解并掌握向量方法解决立体几何夹角问题的一般方法; 3.根据题意,把立体几何问题转化为向量问题.
教学重点、难点: 教学重点:理解并掌握向量方法解决立体几何夹角问题的一般方法。 教学难点:根据题意,把立体几何问题转化为向量问题。
教学过程
教学环节 教学过程
创设情境 【视频引入】播放达瓦孜在露天进行表演,以及我国的PLZ-05自行火炮, 舰载机的偏流板的视频。 [提问] 1.达瓦孜表演多在露天进行,表演者手持长约6米的平衡杆,不系任何保险带,在绳索上行走,表演中,平衡杆和钢丝绳就像是分处不同平面的两条直线,行走过程中平衡杆和钢丝绳有夹角吗?如果有夹角又如何来求解呢? 2.随着科技的发展与推动,战争利器火炮也在更新进化,在战争中有更高效率的火力支援,火炮在地面射击时,由于空气对弹丸的作用,最大射程角是不一样的,如85加农炮的最大射程角为35度左右,迫击炮、122毫米榴弹炮最大射程角为45度左右。2018全球自行榴弹炮排名中我国的PLZ-05自行火炮居首,它的弹丸初速度930m/s以上,最大射程为70km,最大射程角为50度左右,请问这里所说的射程角是什么? 3.舰载机的偏流板为了发挥最佳效果,它与舰艇夹板的夹角也是有夹角的,经过论证夹角大小一般会选取45°、 60°或 75°。那么这里所说的夹角什么呢? 【教师总结】 1.平衡杆和钢丝绳有夹角,其夹角可以运用空间向量的数量积求解。 2.射程角就是我们数学中所说的直线与平面所成的角。 3.所说的夹角是二面角。
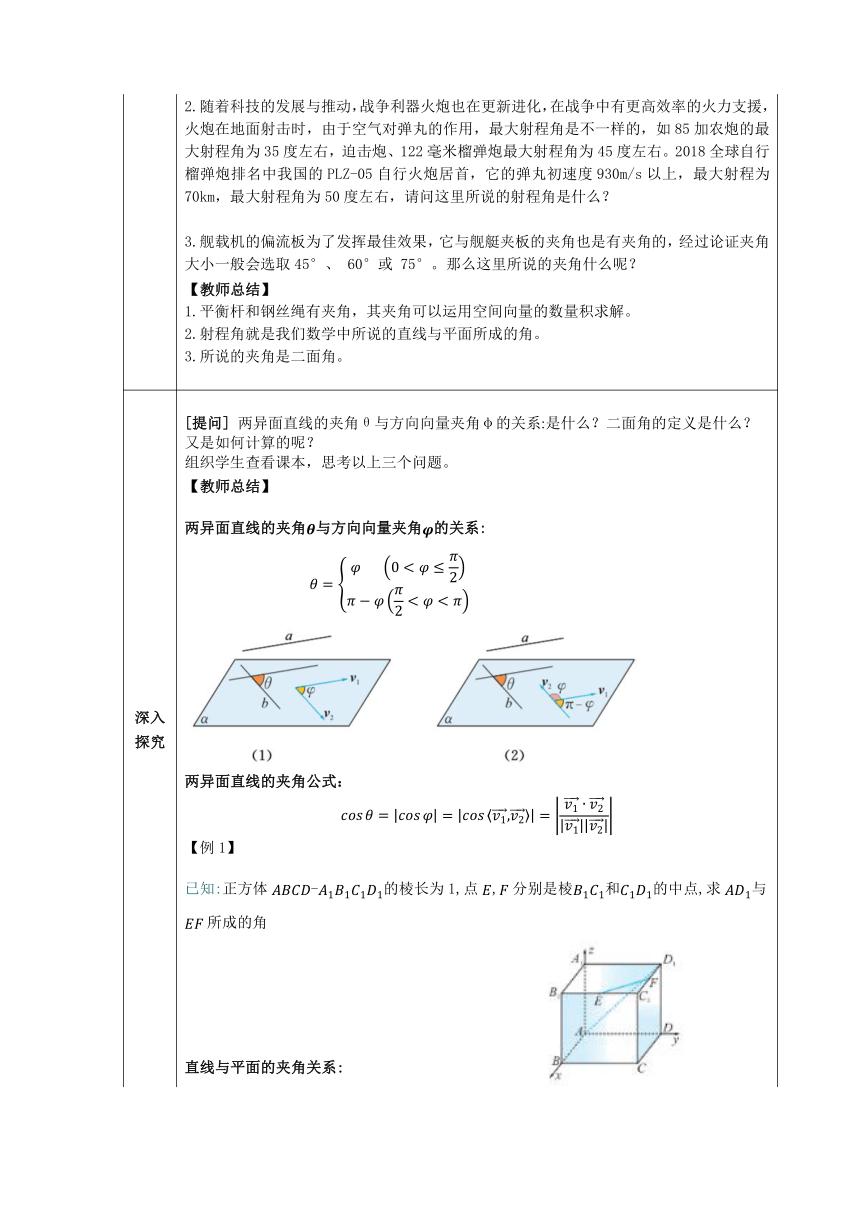
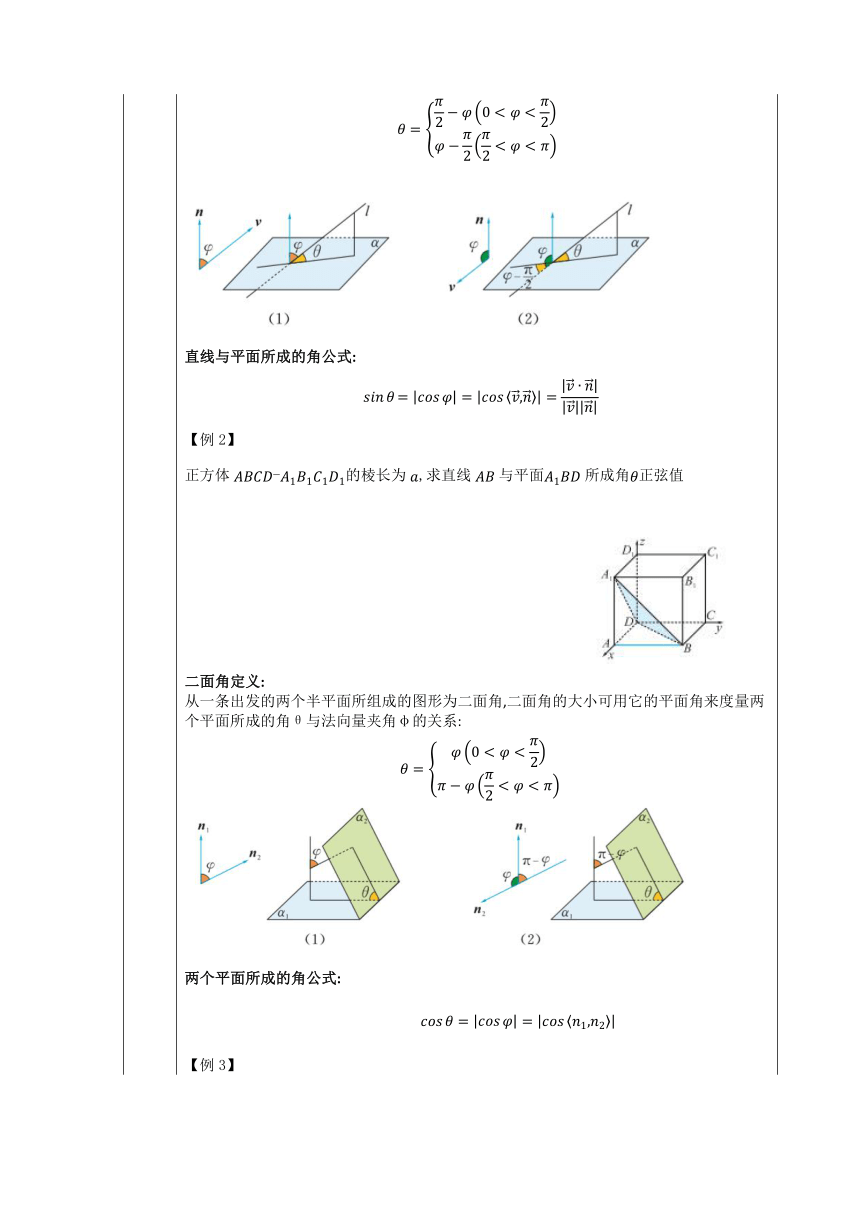
深入探究 [提问] 两异面直线的夹角θ与方向向量夹角φ的关系:是什么?二面角的定义是什么?又是如何计算的呢? 组织学生查看课本,思考以上三个问题。 【教师总结】 两异面直线的夹角与方向向量夹角的关系: 两异面直线的夹角公式: 【例1】 已知:正方体-的棱长为1,点,分别是棱和的中点,求与所成的角 直线与平面的夹角关系: 直线与平面所成的角公式: 【例2】 正方体-的棱长为,求直线与平面所成角正弦值 二面角定义: 从一条出发的两个半平面所组成的图形为二面角,二面角的大小可用它的平面角来度量两个平面所成的角θ与法向量夹角φ的关系: 两个平面所成的角公式: 【例3】 如图2.4-21,正方体-的顶点坐标为 , ,,,,求二面角的余弦值
课堂练习 【练习1】 正三棱柱中,,求与所成角的大小 【练习2】 如图,在空间直角坐标系中有长方体,,,求对角线和侧面对角线的夹角的余弦值 【练习3】 正四面体中棱与底面所成角的余弦值 【练习4】 在长方体中,,,试求与面所成角的正弦值 【练习5】 如图所示 ,四棱锥 的底面是边长为 1的菱形,,是的中点,底面,=2 (1)证明:平面平面 (2)求平面和平面所成二面角(锐角)的大小 【练习6】 如图,在三棱柱 中,已知,,,侧面 (1)求直线与底面所成角正切值: (2)在棱(不包含端点)上确定一点的位置,使得 (3)在(2)的条件下,若,求二面角的大小
课堂小结 1.两异面直线的夹角公式: 2.直线与平面所成的角公式: 3.两个平面所成的角公式:
课后作业 教材练习题1,2,3.
教学方法: “一体二化三导四学”教学模式和自主学习模式. (一体二化三导四学:以学生为主体,教学内容问题化,教学活动探究化,引导,指导,督导,自主学习,探究学习,合作学习,体验学习)
教学目标: 1.掌握异面直线、直线和平面,平面与平面所成的角的向量解法; 2.理解并掌握向量方法解决立体几何夹角问题的一般方法; 3.根据题意,把立体几何问题转化为向量问题.
教学重点、难点: 教学重点:理解并掌握向量方法解决立体几何夹角问题的一般方法。 教学难点:根据题意,把立体几何问题转化为向量问题。
教学过程
教学环节 教学过程
创设情境 【视频引入】播放达瓦孜在露天进行表演,以及我国的PLZ-05自行火炮, 舰载机的偏流板的视频。 [提问] 1.达瓦孜表演多在露天进行,表演者手持长约6米的平衡杆,不系任何保险带,在绳索上行走,表演中,平衡杆和钢丝绳就像是分处不同平面的两条直线,行走过程中平衡杆和钢丝绳有夹角吗?如果有夹角又如何来求解呢? 2.随着科技的发展与推动,战争利器火炮也在更新进化,在战争中有更高效率的火力支援,火炮在地面射击时,由于空气对弹丸的作用,最大射程角是不一样的,如85加农炮的最大射程角为35度左右,迫击炮、122毫米榴弹炮最大射程角为45度左右。2018全球自行榴弹炮排名中我国的PLZ-05自行火炮居首,它的弹丸初速度930m/s以上,最大射程为70km,最大射程角为50度左右,请问这里所说的射程角是什么? 3.舰载机的偏流板为了发挥最佳效果,它与舰艇夹板的夹角也是有夹角的,经过论证夹角大小一般会选取45°、 60°或 75°。那么这里所说的夹角什么呢? 【教师总结】 1.平衡杆和钢丝绳有夹角,其夹角可以运用空间向量的数量积求解。 2.射程角就是我们数学中所说的直线与平面所成的角。 3.所说的夹角是二面角。
深入探究 [提问] 两异面直线的夹角θ与方向向量夹角φ的关系:是什么?二面角的定义是什么?又是如何计算的呢? 组织学生查看课本,思考以上三个问题。 【教师总结】 两异面直线的夹角与方向向量夹角的关系: 两异面直线的夹角公式: 【例1】 已知:正方体-的棱长为1,点,分别是棱和的中点,求与所成的角 直线与平面的夹角关系: 直线与平面所成的角公式: 【例2】 正方体-的棱长为,求直线与平面所成角正弦值 二面角定义: 从一条出发的两个半平面所组成的图形为二面角,二面角的大小可用它的平面角来度量两个平面所成的角θ与法向量夹角φ的关系: 两个平面所成的角公式: 【例3】 如图2.4-21,正方体-的顶点坐标为 , ,,,,求二面角的余弦值
课堂练习 【练习1】 正三棱柱中,,求与所成角的大小 【练习2】 如图,在空间直角坐标系中有长方体,,,求对角线和侧面对角线的夹角的余弦值 【练习3】 正四面体中棱与底面所成角的余弦值 【练习4】 在长方体中,,,试求与面所成角的正弦值 【练习5】 如图所示 ,四棱锥 的底面是边长为 1的菱形,,是的中点,底面,=2 (1)证明:平面平面 (2)求平面和平面所成二面角(锐角)的大小 【练习6】 如图,在三棱柱 中,已知,,,侧面 (1)求直线与底面所成角正切值: (2)在棱(不包含端点)上确定一点的位置,使得 (3)在(2)的条件下,若,求二面角的大小
课堂小结 1.两异面直线的夹角公式: 2.直线与平面所成的角公式: 3.两个平面所成的角公式:
课后作业 教材练习题1,2,3.
同课章节目录
