2.4.4向量与距离(平行线间的距离、平行平面间的距离)教案(表格式)2024-2025学年高二下学期数学湘教版(2019)选择性必修第二册
文档属性
| 名称 | 2.4.4向量与距离(平行线间的距离、平行平面间的距离)教案(表格式)2024-2025学年高二下学期数学湘教版(2019)选择性必修第二册 |

|
|
| 格式 | docx | ||
| 文件大小 | 499.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-12 00:00:00 | ||
图片预览

文档简介
课题名称:数学选择性必修第2册 向量与距离(平行线间的距离、平行平面间的距离)
教学方法: “一体二化三导四学”教学模式和自主学习模式. (一体二化三导四学:以学生为主体,教学内容问题化,教学活动探究化,引导,指导,督导,自主学习,探究学习,合作学习,体验学习)
教学目标: 1.理解平行线间的距离、平行平面间的距离公式的推导; 2.掌握平行线间的距离、平行平面间的距离公式以及应用; 3.能在不同的图形中运用向量法求解平行线间的距离、平行平面间的距离.
教学重点、难点: 教学重点:掌握平行线间的距离、平行平面间的距离公式以及应用; 教学难点:在不同的图形中运用向量法求解平行线间的距离、平行平面间的距离。
教学过程
教学环节 教学过程
创设情境 我们知道两平行线间的距离处处相等,因而可以利用点到直线的距离来解决两平行线间的距离问题。
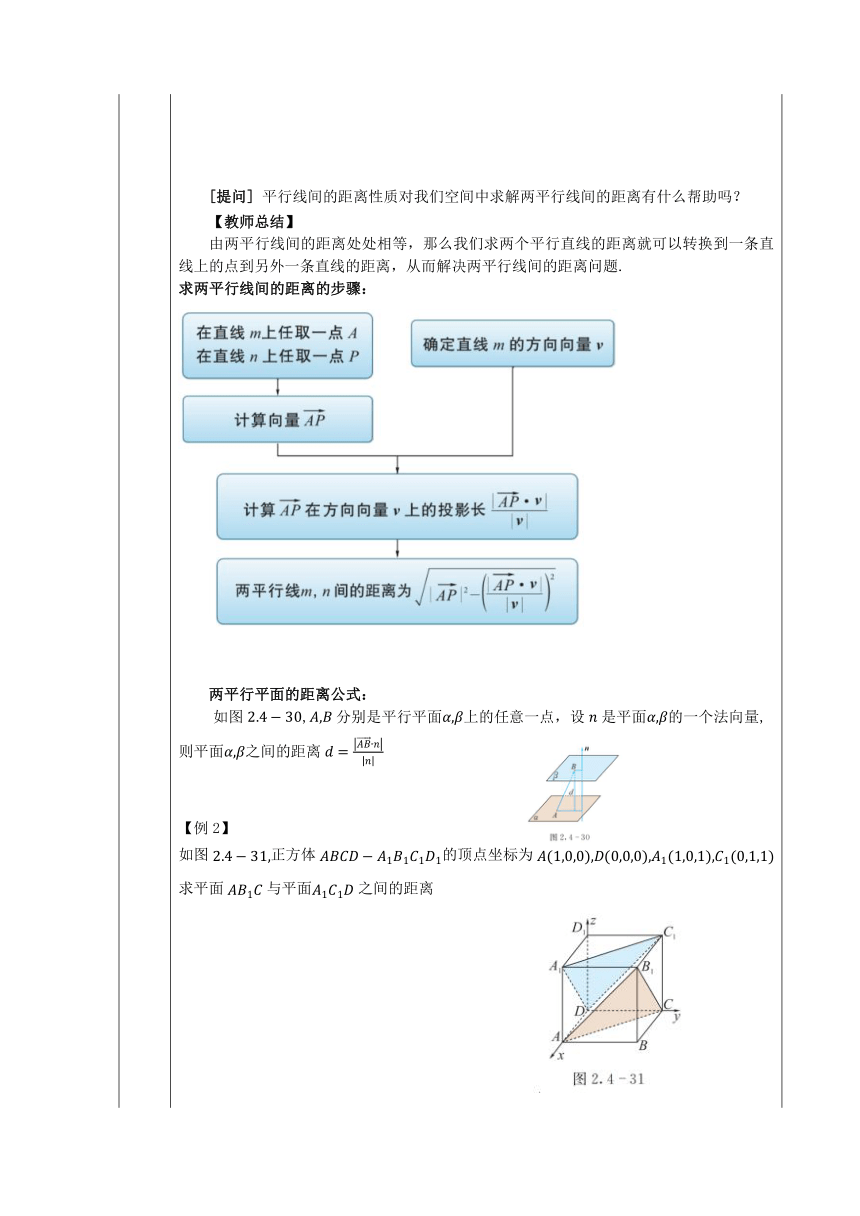
深入探究 【例1】 如图,长方体的顶点坐标为和分别是棱和的中点,求与之间的距离 [提问] 平行线间的距离性质对我们空间中求解两平行线间的距离有什么帮助吗? 【教师总结】 由两平行线间的距离处处相等,那么我们求两个平行直线的距离就可以转换到一条直线上的点到另外一条直线的距离,从而解决两平行线间的距离问题. 求两平行线间的距离的步骤: 两平行平面的距离公式: 如图,分别是平行平面上的任意一点,设是平面的一个法向量,则平面之间的距离 【例2】 如图正方体的顶点坐标为求平面与平面之间的距离 求两平行平面间的距离的步骤:
课堂练习 【练习1】 如图,在单位正方体中,已知为上的一点,且在面内作交于点,求直线与的距离 【练习2】 在正方体中,分别为的中点,棱长为求平面与平面之间的距离 【练习3】 如图,四棱锥的底面是菱形是的中点,侧棱底面且是的中点,求与之间的距离 【练习4】 在棱长为的正方体中,分别是,的中点,求平面与平面之间的距离 【练习5】 已知高为底面边长为的正四棱柱中,点分别为上下两底面的中心,求与之间的距离
课堂小结 1.求两平行线间的距离: 2.求两平行平面的距离公式:
课后作业 教材练习题1,2.
教学方法: “一体二化三导四学”教学模式和自主学习模式. (一体二化三导四学:以学生为主体,教学内容问题化,教学活动探究化,引导,指导,督导,自主学习,探究学习,合作学习,体验学习)
教学目标: 1.理解平行线间的距离、平行平面间的距离公式的推导; 2.掌握平行线间的距离、平行平面间的距离公式以及应用; 3.能在不同的图形中运用向量法求解平行线间的距离、平行平面间的距离.
教学重点、难点: 教学重点:掌握平行线间的距离、平行平面间的距离公式以及应用; 教学难点:在不同的图形中运用向量法求解平行线间的距离、平行平面间的距离。
教学过程
教学环节 教学过程
创设情境 我们知道两平行线间的距离处处相等,因而可以利用点到直线的距离来解决两平行线间的距离问题。
深入探究 【例1】 如图,长方体的顶点坐标为和分别是棱和的中点,求与之间的距离 [提问] 平行线间的距离性质对我们空间中求解两平行线间的距离有什么帮助吗? 【教师总结】 由两平行线间的距离处处相等,那么我们求两个平行直线的距离就可以转换到一条直线上的点到另外一条直线的距离,从而解决两平行线间的距离问题. 求两平行线间的距离的步骤: 两平行平面的距离公式: 如图,分别是平行平面上的任意一点,设是平面的一个法向量,则平面之间的距离 【例2】 如图正方体的顶点坐标为求平面与平面之间的距离 求两平行平面间的距离的步骤:
课堂练习 【练习1】 如图,在单位正方体中,已知为上的一点,且在面内作交于点,求直线与的距离 【练习2】 在正方体中,分别为的中点,棱长为求平面与平面之间的距离 【练习3】 如图,四棱锥的底面是菱形是的中点,侧棱底面且是的中点,求与之间的距离 【练习4】 在棱长为的正方体中,分别是,的中点,求平面与平面之间的距离 【练习5】 已知高为底面边长为的正四棱柱中,点分别为上下两底面的中心,求与之间的距离
课堂小结 1.求两平行线间的距离: 2.求两平行平面的距离公式:
课后作业 教材练习题1,2.
同课章节目录
