第三章 函数及其图象 第一节 图形坐标与函数(含答案)
文档属性
| 名称 | 第三章 函数及其图象 第一节 图形坐标与函数(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 15.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-12 11:06:03 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第三章 函数及其图象
第1节 图形坐标与函数
考点分析
考点1 点的坐标特征
课标要求导航:①理解平面直角坐标系的有关概念,能画出平面直角坐标系;在
给定的平面直角坐标系中,能根据坐标描出点的位置,由点的位置写出坐标;②
在实际问题中,能建立适当的平面直角坐标系,描述物体的位置;③探索简单实
例中的数量关系和变化规律.
例1 某小区的圆形花园中间有两条互相垂直的小路,园丁在花园中栽种了8 棵桂花,如图所示.若A,B两处桂花的位置关于小路对称,在分别以两条小路为x,y轴的平面直角坐标系内,若点A 的坐标为( -6,2),则点 B 的坐标为( )
A. (6,2) B. (-6,-2) C. (2,6)
1.1 传统文化 如图是中国象棋棋盘的一部分,建立如图所示的平面直角坐标系,已知“車”所在位置的坐标为 则“炮”所在位置的坐标为 ( )
A. (3,1) B. (1,3) C. (4,1) D. (3,2)
1.2 如果单项式 与单项式 的和仍是一个单项式,则在平面直角坐标系中点(m,n)在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
1.3 在直角坐标系中,把点A(m,2)先向右平移1个单位,再向上平移3个单位得到点 B.若点 B 的横坐标和纵坐标相等,则( )
A. 2 B. 3 C. 4 D. 5
例2 跨体育学科 2024年5月5 日在四川成都举行的“尤伯杯”羽毛球团体决赛中,中国队第16次夺得冠军.如图1是比赛场馆图,图2是场馆某正方形座位示意图.小李、小亮、小东的座位如图所示(网格中,每个小正方形的边长都是1).若小亮的座位用( -1,0)表示,小李的座位用(1,3)表示,则小东的座位可以表示为 ( )
A. (-1,2) C. (3,-1) D. (1,2)
2.1 传统文化 “计里画方”是中国古代一种按比例尺绘制地图的传统方法,绘图时先在图上布满方格,然后按方格绘制地图内容.小华按照“计里画方”的方法,绘制了蒙山大佛旅游区的局部示意图(如图).若该图中“开化寺”与“蒙山晓月”两处景点的坐标分别为 则景点“蒙山氧吧”的坐标为 ( )
B.(-2,5) C.(-2,2)
例3 任取一个正整数,若是奇数,就将该数乘3再加上1;若是偶数,就将该数除以2.反复进行上述两种运算,经过有限次运算后,必进入循环圈1→4→2→1,这就是“冰雹猜想”.在平面直角坐标系xOy中,将点(x,y)中的x,y分别按照“冰雹猜想”同步进行运算得到新的点的横、纵坐标,其中x,y均为正整数.例如,点(6,3)经过第1次运算得到点(3,10),经过第2次运算得到点(10,5),以此类推.则点(1,4)经过2 024次运算后得到点___________.
3.1 规律探究 如图,小好同学用计算机软件绘制函数 的图象,发现它关于点(1,0)中心对称.若点 )都在函数图象上,这20个点的横坐标从0.1开始依次增加0.1,则 的值是 ( )
A. - 1 B. -0.729 C. 0 D. 1
考点2 求函数自变量的取值范围
课标要求导航:①了解常量、变量的意义;②了解函数的概念和表示法,能举出函数的实例;③能确定简单实际问题中函数自变量的取值范围,会求函数值.
例4 若函数 的解析式在实数范围内有意义,则自变量x的取值范围是___________.
4.1 函数 中,自变量x的取值范围是____________.
例5 已知等腰三角形的周长为10 cm,将底边长y cm表示为腰长 x cm的关系式是y=10-2x,则其自变量x的取值范围是 ( )
C.一切实数
考点3 函数图象
课标要求导航:①能用适当的函数表示法刻画简单实际问题中变量之间的关系,理解函数值的意义;②结合对函数关系的分析,能对变量的变化情况进行初步讨论;③能结合图象对简单实际问题中的函数关系进行分析.
例6 跨化学学科 由化学知识可知,用pH 表示溶液酸碱性的强弱程度,当 时溶液呈碱性,当 时溶液呈酸性,若将给定的NaOH溶液加水稀释,那么在下列图象中,能大致反映NaOH 溶液的pH与所加水的体积V之间对应关系的是 ( )
6.1 周末的早晨王老师从家出发去燕山公园锻炼,她连续、匀速走了60 min后回到家.如图线段OA-AB-BC 是她出发后所在位置离家的距离s(km)与行走时间t(min)之间的函数关系,则下列图形中可以大致描述王老师行走的路线是 ( )
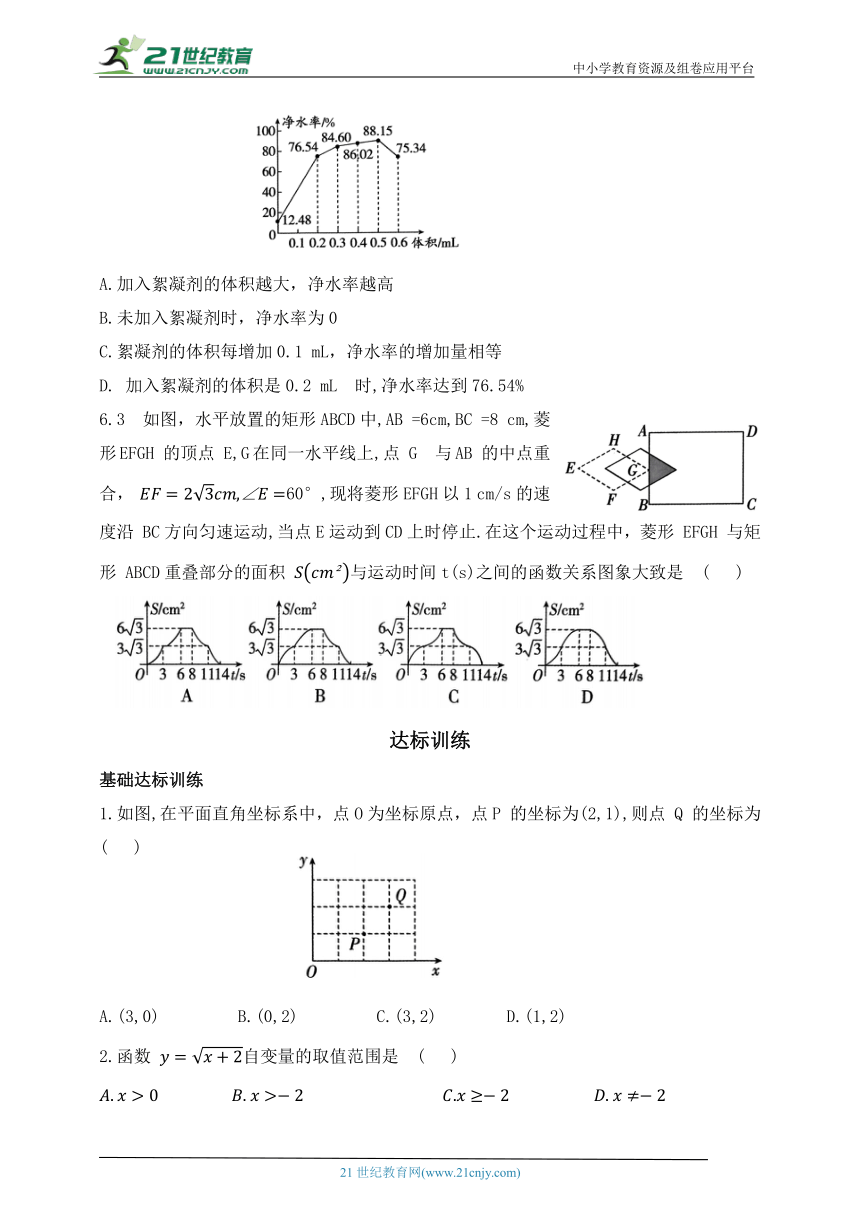
6.2 跨化学学科 化学实验小组查阅资料了解到:某种絮凝剂溶于水后能够吸附水中悬浮物并发生沉降,从而达到净水的目的.实验得出加入絮凝剂的体积与净水率之间的关系如图所示,下列说法正确的是 ( )
A.加入絮凝剂的体积越大,净水率越高
B.未加入絮凝剂时,净水率为0
C.絮凝剂的体积每增加0.1 mL,净水率的增加量相等
D. 加入絮凝剂的体积是0.2 mL 时,净水率达到76.54%
6.3 如图,水平放置的矩形ABCD中,AB =6cm,BC =8 cm,菱形EFGH 的顶点 E,G在同一水平线上,点 G 与AB 的中点重合, 60°,现将菱形EFGH以1 cm/s的速度沿 BC方向匀速运动,当点E运动到CD上时停止.在这个运动过程中,菱形 EFGH 与矩形 ABCD重叠部分的面积 与运动时间t(s)之间的函数关系图象大致是 ( )
达标训练
基础达标训练
1.如图,在平面直角坐标系中,点O为坐标原点,点P 的坐标为(2,1),则点 Q 的坐标为 ( )
A.(3,0) B.(0,2) C.(3,2) D.(1,2)
2.函数 自变量的取值范围是 ( )
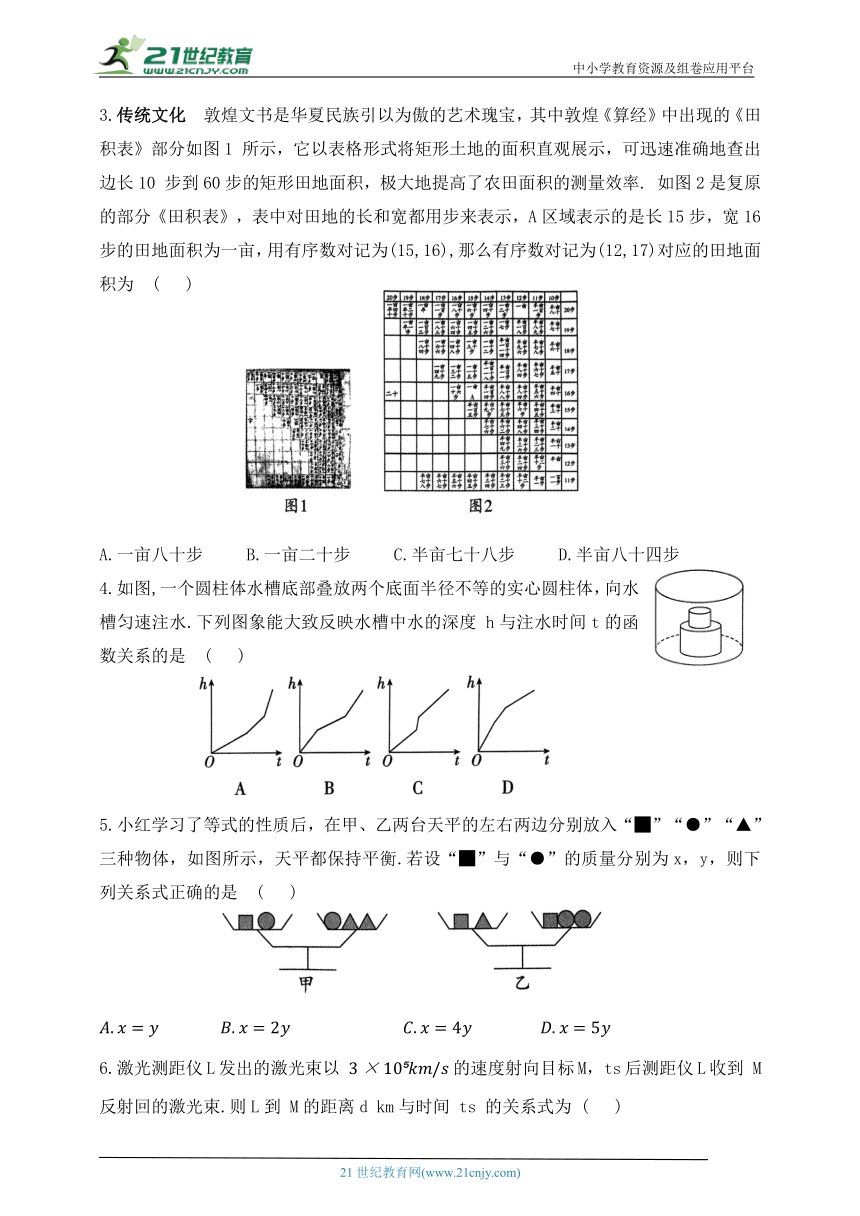
3.传统文化 敦煌文书是华夏民族引以为傲的艺术瑰宝,其中敦煌《算经》中出现的《田积表》部分如图1 所示,它以表格形式将矩形土地的面积直观展示,可迅速准确地查出边长10 步到60步的矩形田地面积,极大地提高了农田面积的测量效率. 如图2是复原的部分《田积表》,表中对田地的长和宽都用步来表示,A区域表示的是长15步,宽16步的田地面积为一亩,用有序数对记为(15,16),那么有序数对记为(12,17)对应的田地面积为 ( )
A.一亩八十步 B.一亩二十步 C.半亩七十八步 D.半亩八十四步
4.如图,一个圆柱体水槽底部叠放两个底面半径不等的实心圆柱体,向水槽匀速注水.下列图象能大致反映水槽中水的深度 h与注水时间t的函数关系的是 ( )
5.小红学习了等式的性质后,在甲、乙两台天平的左右两边分别放入“█”“●”“▲”三种物体,如图所示,天平都保持平衡.若设“█”与“●”的质量分别为x,y,则下列关系式正确的是 ( )
6.激光测距仪L发出的激光束以 的速度射向目标M, ts后测距仪L收到 M 反射回的激光束.则L到 M的距离d km与时间 ts 的关系式为 ( )
高分提能特训
7.如图1,矩形 ABCD 中,BD 为其对角线,一动点 P 从D 出发,沿着 D→B→C 的路径行进,过点 P 作垂足为Q.设点 P 的运动路程为x,PQ-DQ 为y,y与x的函数图象如图2,则AD 的长为 ( )
8.(如图,在等腰 中,动点 E,F同时从点A 出发,分别沿射线AB 和射线AC 的方向匀速运动,且速度大小相同,当点 E 停止运动时,点F 也随之停止运动,连接EF,以EF为边向下做正方形 EFGH,设点 E 运动的路程为 正方形 EFGH 和等腰重合部分的面积为y.下列图象能反映y与x之间函数关系的是 ( )
9.跨学科·物理 把多个用电器连接在同一个插线板上,同时使用一段时间后,插线板的电源线会明显发热,存在安全隐患.数学兴趣小组对这种现象进行研究,得到时长一定时,插线板电源线中的电流I与使用电器的总功率 P 的函数图象(如图1),插线板电源线产生的热量Q 与I的函数图象(如图2).下列结论中错误的是 ( )
A.当P=440 W时,I=2 A B. Q随I的增大而增大
C. I每增加1 A,Q 的增加量相同 D. P越大,插线板电源线产生的热量Q 越多
10.如图,在一个平面区域内,一台雷达探测器测得在点 A,B,C处有目标出现.按某种规则,点A,B的位置可以分别表示为 则点 C 的位置可以表示为_____________.
冲刺满分特训
11.如图是一位旅行者在早晨8时从城市出发到郊外全程所走的路程S(千米)与时间t(时)之间的关系图象.
根据图象回答问题:
(1)在这个变化过程中,自变量是__________,因变量是__________;
(2)他一共走了多少千米 在途中休息了多长时间
(3)他休息前的平均速度是多少千米/时
参考答案
考点分析
【例1】 A 1.1 A 1.2 D 1.3 C
【例2】 C 2.1 C
【例3】 (2,1) 3.1 D
【例4】 x≠1 4.1 x≥-3且
【例5】 B
【例6】 B 6.1 A 6.2 D
6.3 D 解析:如图1所示,设EG,HF 交于点 O.
在菱形 EFGH 中, ∴ △HFG 是等边三角形.
∵ EF =
当时,重合部分为 如图2所示.
依题意,△MNG为等边三角形.运动时间为 ts,则
当 时,如图3所示.
依题意, 则
∴当 时, 当 时,如
图4所示,同理可得,
当 时,如图5所示,同理可得,
综上所述,当( 时,函数图象为开口向上的一段抛物线;当 时,函数图象为开口向下的一段抛物线;当( 时,函数图象为一条线段;当 时,函数图象为开口向下的一段抛物线;当时,函数图象为开口向上的一段抛物线.
达标训练
1. C 2. C 3. D
4. D 解析:下层圆柱底面半径大,水面上升快,上层圆柱底面半径稍小,水面上升稍慢,再往上则水面上升更慢,所以对应图象是第一段比较陡,第二段比第一段缓,第三段比第二段缓.
5. C 解析:设“▲”的质量为 z.根据甲天平,得 ,根据乙天平,得 .由①,得x由②,得 x
6. A
7. B 解析:由图象,得当BD 时,
设 则
在 中,即 解得
8. A 解析:在解析该题之前我们一定要对此类面积问题的动点函数图象有判断方法,切不可小题大作,去把每一个解析式求出来再判断,那是此类题型最不优先考虑的解法. 面积问题函数图象判断方法:①底和高一个是定值一个是变量,则图象是一次函数,如果变量是增加的,则是 y随x增大而增大的一次函数;如果变量是减小的,则是y 随x增大而减小的一次函数;②底和高两个都是变量,则函数图象一定是二次函数,两个变量同增或同减,则是开口向上的二次函数;两个变量一增一减,则是开口向下的二次函数.运用:本题中正方形 EFGH 与等腰 的重合部分主要分两部分.①当重合部分全部在等腰 内部时,我们发现重合部分实际就是正方形 EFGH 的面积,此时正方形边长在增大,就是底和高同增,所以这一部分是开口向上的二次函数,选项只有A,B符合;②当重合部分是正方形 EFGH 的一部分时,我们发现这一部分的长在增大,但是宽在减小,就是底和高一增一减,所以这一部分是开口向下的二次函数,选项A符合.
9. C 10.(3,30°)
11.解:(1)时间,路程.
(2)由图可知,他一共走了15千米.
(小时),∴ 他休息了0.5 小时.
(千米/时).
答:他休息前的平均速度是4.5千米/时.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第三章 函数及其图象
第1节 图形坐标与函数
考点分析
考点1 点的坐标特征
课标要求导航:①理解平面直角坐标系的有关概念,能画出平面直角坐标系;在
给定的平面直角坐标系中,能根据坐标描出点的位置,由点的位置写出坐标;②
在实际问题中,能建立适当的平面直角坐标系,描述物体的位置;③探索简单实
例中的数量关系和变化规律.
例1 某小区的圆形花园中间有两条互相垂直的小路,园丁在花园中栽种了8 棵桂花,如图所示.若A,B两处桂花的位置关于小路对称,在分别以两条小路为x,y轴的平面直角坐标系内,若点A 的坐标为( -6,2),则点 B 的坐标为( )
A. (6,2) B. (-6,-2) C. (2,6)
1.1 传统文化 如图是中国象棋棋盘的一部分,建立如图所示的平面直角坐标系,已知“車”所在位置的坐标为 则“炮”所在位置的坐标为 ( )
A. (3,1) B. (1,3) C. (4,1) D. (3,2)
1.2 如果单项式 与单项式 的和仍是一个单项式,则在平面直角坐标系中点(m,n)在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
1.3 在直角坐标系中,把点A(m,2)先向右平移1个单位,再向上平移3个单位得到点 B.若点 B 的横坐标和纵坐标相等,则( )
A. 2 B. 3 C. 4 D. 5
例2 跨体育学科 2024年5月5 日在四川成都举行的“尤伯杯”羽毛球团体决赛中,中国队第16次夺得冠军.如图1是比赛场馆图,图2是场馆某正方形座位示意图.小李、小亮、小东的座位如图所示(网格中,每个小正方形的边长都是1).若小亮的座位用( -1,0)表示,小李的座位用(1,3)表示,则小东的座位可以表示为 ( )
A. (-1,2) C. (3,-1) D. (1,2)
2.1 传统文化 “计里画方”是中国古代一种按比例尺绘制地图的传统方法,绘图时先在图上布满方格,然后按方格绘制地图内容.小华按照“计里画方”的方法,绘制了蒙山大佛旅游区的局部示意图(如图).若该图中“开化寺”与“蒙山晓月”两处景点的坐标分别为 则景点“蒙山氧吧”的坐标为 ( )
B.(-2,5) C.(-2,2)
例3 任取一个正整数,若是奇数,就将该数乘3再加上1;若是偶数,就将该数除以2.反复进行上述两种运算,经过有限次运算后,必进入循环圈1→4→2→1,这就是“冰雹猜想”.在平面直角坐标系xOy中,将点(x,y)中的x,y分别按照“冰雹猜想”同步进行运算得到新的点的横、纵坐标,其中x,y均为正整数.例如,点(6,3)经过第1次运算得到点(3,10),经过第2次运算得到点(10,5),以此类推.则点(1,4)经过2 024次运算后得到点___________.
3.1 规律探究 如图,小好同学用计算机软件绘制函数 的图象,发现它关于点(1,0)中心对称.若点 )都在函数图象上,这20个点的横坐标从0.1开始依次增加0.1,则 的值是 ( )
A. - 1 B. -0.729 C. 0 D. 1
考点2 求函数自变量的取值范围
课标要求导航:①了解常量、变量的意义;②了解函数的概念和表示法,能举出函数的实例;③能确定简单实际问题中函数自变量的取值范围,会求函数值.
例4 若函数 的解析式在实数范围内有意义,则自变量x的取值范围是___________.
4.1 函数 中,自变量x的取值范围是____________.
例5 已知等腰三角形的周长为10 cm,将底边长y cm表示为腰长 x cm的关系式是y=10-2x,则其自变量x的取值范围是 ( )
C.一切实数
考点3 函数图象
课标要求导航:①能用适当的函数表示法刻画简单实际问题中变量之间的关系,理解函数值的意义;②结合对函数关系的分析,能对变量的变化情况进行初步讨论;③能结合图象对简单实际问题中的函数关系进行分析.
例6 跨化学学科 由化学知识可知,用pH 表示溶液酸碱性的强弱程度,当 时溶液呈碱性,当 时溶液呈酸性,若将给定的NaOH溶液加水稀释,那么在下列图象中,能大致反映NaOH 溶液的pH与所加水的体积V之间对应关系的是 ( )
6.1 周末的早晨王老师从家出发去燕山公园锻炼,她连续、匀速走了60 min后回到家.如图线段OA-AB-BC 是她出发后所在位置离家的距离s(km)与行走时间t(min)之间的函数关系,则下列图形中可以大致描述王老师行走的路线是 ( )
6.2 跨化学学科 化学实验小组查阅资料了解到:某种絮凝剂溶于水后能够吸附水中悬浮物并发生沉降,从而达到净水的目的.实验得出加入絮凝剂的体积与净水率之间的关系如图所示,下列说法正确的是 ( )
A.加入絮凝剂的体积越大,净水率越高
B.未加入絮凝剂时,净水率为0
C.絮凝剂的体积每增加0.1 mL,净水率的增加量相等
D. 加入絮凝剂的体积是0.2 mL 时,净水率达到76.54%
6.3 如图,水平放置的矩形ABCD中,AB =6cm,BC =8 cm,菱形EFGH 的顶点 E,G在同一水平线上,点 G 与AB 的中点重合, 60°,现将菱形EFGH以1 cm/s的速度沿 BC方向匀速运动,当点E运动到CD上时停止.在这个运动过程中,菱形 EFGH 与矩形 ABCD重叠部分的面积 与运动时间t(s)之间的函数关系图象大致是 ( )
达标训练
基础达标训练
1.如图,在平面直角坐标系中,点O为坐标原点,点P 的坐标为(2,1),则点 Q 的坐标为 ( )
A.(3,0) B.(0,2) C.(3,2) D.(1,2)
2.函数 自变量的取值范围是 ( )
3.传统文化 敦煌文书是华夏民族引以为傲的艺术瑰宝,其中敦煌《算经》中出现的《田积表》部分如图1 所示,它以表格形式将矩形土地的面积直观展示,可迅速准确地查出边长10 步到60步的矩形田地面积,极大地提高了农田面积的测量效率. 如图2是复原的部分《田积表》,表中对田地的长和宽都用步来表示,A区域表示的是长15步,宽16步的田地面积为一亩,用有序数对记为(15,16),那么有序数对记为(12,17)对应的田地面积为 ( )
A.一亩八十步 B.一亩二十步 C.半亩七十八步 D.半亩八十四步
4.如图,一个圆柱体水槽底部叠放两个底面半径不等的实心圆柱体,向水槽匀速注水.下列图象能大致反映水槽中水的深度 h与注水时间t的函数关系的是 ( )
5.小红学习了等式的性质后,在甲、乙两台天平的左右两边分别放入“█”“●”“▲”三种物体,如图所示,天平都保持平衡.若设“█”与“●”的质量分别为x,y,则下列关系式正确的是 ( )
6.激光测距仪L发出的激光束以 的速度射向目标M, ts后测距仪L收到 M 反射回的激光束.则L到 M的距离d km与时间 ts 的关系式为 ( )
高分提能特训
7.如图1,矩形 ABCD 中,BD 为其对角线,一动点 P 从D 出发,沿着 D→B→C 的路径行进,过点 P 作垂足为Q.设点 P 的运动路程为x,PQ-DQ 为y,y与x的函数图象如图2,则AD 的长为 ( )
8.(如图,在等腰 中,动点 E,F同时从点A 出发,分别沿射线AB 和射线AC 的方向匀速运动,且速度大小相同,当点 E 停止运动时,点F 也随之停止运动,连接EF,以EF为边向下做正方形 EFGH,设点 E 运动的路程为 正方形 EFGH 和等腰重合部分的面积为y.下列图象能反映y与x之间函数关系的是 ( )
9.跨学科·物理 把多个用电器连接在同一个插线板上,同时使用一段时间后,插线板的电源线会明显发热,存在安全隐患.数学兴趣小组对这种现象进行研究,得到时长一定时,插线板电源线中的电流I与使用电器的总功率 P 的函数图象(如图1),插线板电源线产生的热量Q 与I的函数图象(如图2).下列结论中错误的是 ( )
A.当P=440 W时,I=2 A B. Q随I的增大而增大
C. I每增加1 A,Q 的增加量相同 D. P越大,插线板电源线产生的热量Q 越多
10.如图,在一个平面区域内,一台雷达探测器测得在点 A,B,C处有目标出现.按某种规则,点A,B的位置可以分别表示为 则点 C 的位置可以表示为_____________.
冲刺满分特训
11.如图是一位旅行者在早晨8时从城市出发到郊外全程所走的路程S(千米)与时间t(时)之间的关系图象.
根据图象回答问题:
(1)在这个变化过程中,自变量是__________,因变量是__________;
(2)他一共走了多少千米 在途中休息了多长时间
(3)他休息前的平均速度是多少千米/时
参考答案
考点分析
【例1】 A 1.1 A 1.2 D 1.3 C
【例2】 C 2.1 C
【例3】 (2,1) 3.1 D
【例4】 x≠1 4.1 x≥-3且
【例5】 B
【例6】 B 6.1 A 6.2 D
6.3 D 解析:如图1所示,设EG,HF 交于点 O.
在菱形 EFGH 中, ∴ △HFG 是等边三角形.
∵ EF =
当时,重合部分为 如图2所示.
依题意,△MNG为等边三角形.运动时间为 ts,则
当 时,如图3所示.
依题意, 则
∴当 时, 当 时,如
图4所示,同理可得,
当 时,如图5所示,同理可得,
综上所述,当( 时,函数图象为开口向上的一段抛物线;当 时,函数图象为开口向下的一段抛物线;当( 时,函数图象为一条线段;当 时,函数图象为开口向下的一段抛物线;当时,函数图象为开口向上的一段抛物线.
达标训练
1. C 2. C 3. D
4. D 解析:下层圆柱底面半径大,水面上升快,上层圆柱底面半径稍小,水面上升稍慢,再往上则水面上升更慢,所以对应图象是第一段比较陡,第二段比第一段缓,第三段比第二段缓.
5. C 解析:设“▲”的质量为 z.根据甲天平,得 ,根据乙天平,得 .由①,得x由②,得 x
6. A
7. B 解析:由图象,得当BD 时,
设 则
在 中,即 解得
8. A 解析:在解析该题之前我们一定要对此类面积问题的动点函数图象有判断方法,切不可小题大作,去把每一个解析式求出来再判断,那是此类题型最不优先考虑的解法. 面积问题函数图象判断方法:①底和高一个是定值一个是变量,则图象是一次函数,如果变量是增加的,则是 y随x增大而增大的一次函数;如果变量是减小的,则是y 随x增大而减小的一次函数;②底和高两个都是变量,则函数图象一定是二次函数,两个变量同增或同减,则是开口向上的二次函数;两个变量一增一减,则是开口向下的二次函数.运用:本题中正方形 EFGH 与等腰 的重合部分主要分两部分.①当重合部分全部在等腰 内部时,我们发现重合部分实际就是正方形 EFGH 的面积,此时正方形边长在增大,就是底和高同增,所以这一部分是开口向上的二次函数,选项只有A,B符合;②当重合部分是正方形 EFGH 的一部分时,我们发现这一部分的长在增大,但是宽在减小,就是底和高一增一减,所以这一部分是开口向下的二次函数,选项A符合.
9. C 10.(3,30°)
11.解:(1)时间,路程.
(2)由图可知,他一共走了15千米.
(小时),∴ 他休息了0.5 小时.
(千米/时).
答:他休息前的平均速度是4.5千米/时.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
