2024-2025学年人教版数学八年级上册期末培优卷(含答案)
文档属性
| 名称 | 2024-2025学年人教版数学八年级上册期末培优卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 418.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-13 15:56:02 | ||
图片预览



文档简介
2024-2025学年人教版数学八年级上册期末培优卷
学校:___________姓名:___________班级:___________学号:___________
一、单选题
1.以下列长度的各组线段为边,能组成三角形的是( )
A.2cm,4cm,6cm B.2cm,5cm,9cm
C.7cm,8cm,cm D.6cm,6cm,cm
2.科学家发现世界上最小的开花结果植物是澳大利亚的出水浮萍,这种植物的果实像一个微小的无花果,质量只有0.000000076克,0.000000076用科学记数法表示是( )
A. B. C. D.
3.在下列多项式的乘法中,可以用平方差公式计算的是( )
A. B.
C. D.
4.如图,在平面直角坐标系中,点A在第一象限,与x轴的夹角为,点P是x轴上一动点,若以P,O,A为顶点的三角形是等腰三角形,则满足条件的点P共有( )
A.2个 B.3个 C.4个 D.6个
5.小李同学制作了如图所示的卡片类、类、类各10张,其中、两类卡片都是正方形,类卡片是长方形.现要拼一个两边分别是和的大长方形,那么下列关于他所准备的类卡片的张数的说法中,正确的是( )
A.够用,剩余5张 B.够用,剩余1张
C.不够用,缺2张 D.不够用,缺3张
6.若2×8m×16m=229,则m的值是( )
A.3 B.4 C.5 D.6
7.如图,在△ABC中, AB的垂直平分线交AB于点D,AD=5cm,交边AC于点E,△BCE的周长等于18cm,则△ABC的周长等于( )
A.23cm B.25cm C.28cm D.30cm
8.如图,小虎用块高度都是的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(,),点C在上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离的长度为( )
A. B. C. D.
9.“绿水青山就是金山银山”.为改造太湖水质,某工程队对2400平方公里的水域进行水质净化,实际工作时每天的工作效率比原计划提高了20%,结果提前了40天完成任务.设实际每天净化的水域面积为x平方公里,则下列方程中正确的是( )
A. B.
C. D.
10.如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF,以下结论:①AD∥BC,②∠ACB=∠ADB,③∠ADC+∠ABD=90°,④∠ADB=45°﹣∠CDB,其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.分解因式: .
12.若,则p的值是 .
13.如图所示,在中,,直线,分别与边交于两点,则 .
14.已知的展开式中不含项,常数项是,则 .
15.若关于x的方程 无解,则m的值是 .
16.如图,于点,于点,,点从点出发以的速度向点运动(到达点停止运动),点从点出发沿着方向运动,、两点同时出发,同时停止运动,若与点、、所构成的三角形全等,则点运动的速度为 .
17.如图,在的边上取点,连接,平分,平分,若,的面积是2,的面积是6,则的长是 .
18.如图,在第1个中,,,往上取一点,延长到,使得;在上取一点,延长到,使得;…;按此作法进行下去,第个三角形中以为顶点的内角的度数为 .
三、解答题
19.完成下列各题
(1)化简; (2)分解因式.
20.(1)先化简,得求值:,其中.
(2)先化简,再求值:,其中.
21.解方程:
(1) (2)
22.如图,的顶点都在格点上,点A坐标为.
(1)将沿y轴正方向平移3个单位长度,得到,画出,并写出点的坐标;
(2)画出关于直线对称的,并写出点的坐标.
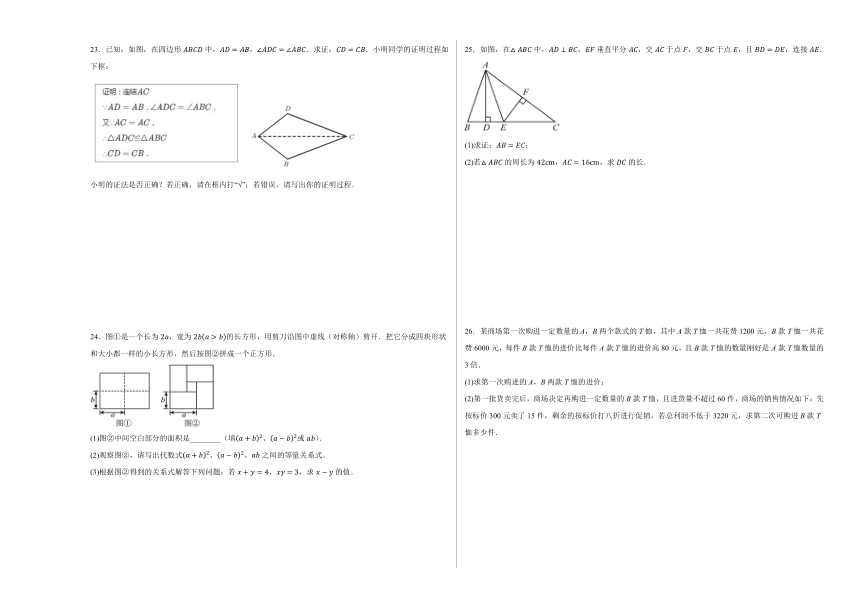
23.已知:如图,在四边形中,,.求证:.小明同学的证明过程如下框:
小明的证法是否正确?若正确,请在框内打“√”;若错误,请写出你的证明过程.
24.图①是一个长为,宽为的长方形,用剪刀沿图中虚线(对称轴)剪开.把它分成四块形状和大小都一样的小长方形,然后按图②拼成一个正方形.
(1)图②中间空白部分的面积是________(填、或).
(2)观察图②,请写出代数式、、之间的等量关系式.
(3)根据图②得到的关系式解答下列问题:若,,求的值.
25.如图,在中,,垂直平分,交于点F,交于点E,且,连接.
(1)求证:;
(2)若的周长为,,求的长.
26.某商场第一次购进一定数量的A,B两个款式的T恤,其中A款T恤一共花费1200元,B款T恤一共花费6000元,每件B款T恤的进价比每件A款T恤的进价高80元,且B款T恤的数量刚好是A款T恤数量的3倍.
(1)求第一次购进的A,B两款T恤的进价;
(2)第一批货卖完后,商场决定再购进一定数量的B款T恤,且进货量不超过60件,商场的销售情况如下:先按标价300元卖了15件,剩余的按标价打八折进行促销,若总利润不低于3220元,求第二次可购进B款T恤多少件.
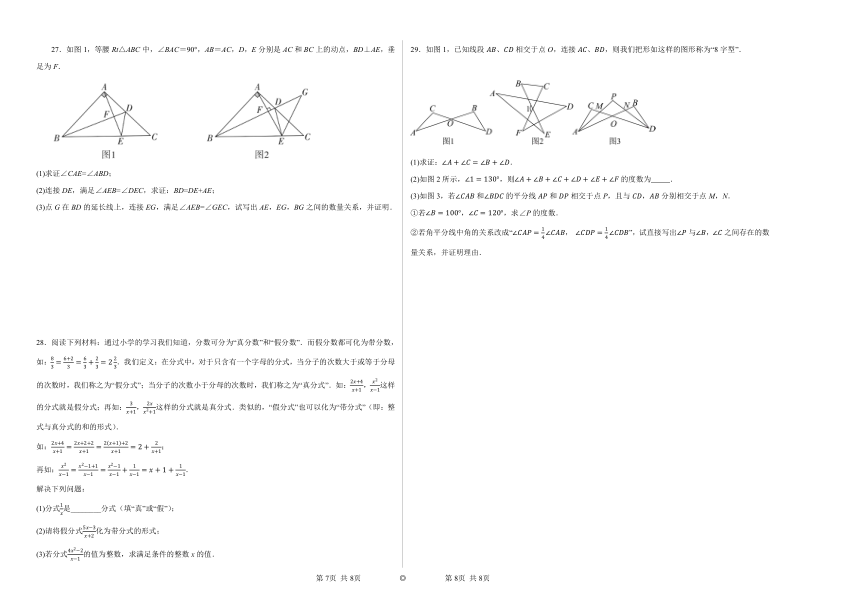
27.如图1,等腰Rt△ABC中,∠BAC=90°,AB=AC,D,E分别是AC和BC上的动点,BD⊥AE,垂足为F.
(1)求证∠CAE=∠ABD;
(2)连接DE,满足∠AEB=∠DEC,求证:BD=DE+AE;
(3)点G在BD的延长线上,连接EG,满足∠AEB=∠GEC,试写出AE,EG,BG之间的数量关系,并证明.
28.阅读下列材料:通过小学的学习我们知道,分数可分为“真分数”和“假分数”.而假分数都可化为带分数,如:.我们定义:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.如:,这样的分式就是假分式;再如:,这样的分式就是真分式.类似的,“假分式”也可以化为“带分式”(即:整式与真分式的和的形式).
如:;
再如:.
解决下列问题:
(1)分式是________分式(填“真”或“假”);
(2)请将假分式化为带分式的形式;
(3)若分式的值为整数,求满足条件的整数x的值.
29.如图1,已知线段、相交于点O,连接、,则我们把形如这样的图形称为“8字型”.
(1)求证:.
(2)如图2所示,,则的度数为 .
(3)如图3,若和的平分线和相交于点P,且与,分别相交于点M,N.
①若,,求∠P的度数.
②若角平分线中角的关系改成“, ”,试直接写出与,之间存在的数量关系,并证明理由.
第1页 共4页 ◎ 第2页 共4页
参考答案
1.C
2.B
3.C
4.A
5.D
6.B
7.C
8.A
9.C
10.B
11.
12.
13.
14.
15.或
16.4或
17.8
18.
19.(1)解:
;
(2)解:
.
20.解:(1)
当时,原式.
(2)
当时,原式.
21.(1)解:方程两边同乘以得
,
解得:,
检验:当时,
,
是原方程的解;
(2)解:方程两边同乘以()得
,
解得:,
检验:当时,,
是原方程的解.
22.(1)解:如图所示:即为所求;点坐标为.
(2)如图所示:,即为所求,点的坐标为.
23.小明的证法错误;
证明:连接.
∵,∴,
又∵,∴,
为等腰三角形,
∴.
24.(1)解:由图形可知:空白部分的面积.
(2)解:由图②可知:大正方形面积=空白部分的面积+4个长方形面积,
∴;
(3)解:∵,
∴,
∵,,
∴,
∴.
25.(1)证明:垂直平分,
,
,,
垂直平分,
,
;
(2)解:的周长为,
,
,
,
,,
.
26.(1)解:设第一次购进的款恤的进价为元,则款恤的进价为元,
由题意得:,
解得:,
经检验,是原方程的解,且符合题意,
,
答:第一次购进的款恤的进价为120元,款恤的进价为200元;
(2)解:设第二次可购进款恤件,
由题意得:,
解得:,
为正整数,
或59或60,
答:第二次可购进款恤58件或59件或60件.
27.(1)
证明:∵BD⊥AF,
∴∠BFA=90°,
∵∠CAE+∠BAF=90°,∠ABD+∠BAF=90°
∴∠CAE=∠ABD.
(2)
证明:如图,作CM⊥AD于点C,CM交AE的延长线于点M
由①知,∠CAE=∠ABD
在△ABD和△CAM中,,
∴△ABD≌△CAM(ASA)
∴BD=AM,
∵∠AEB=∠CEM,
∴∠DEC=∠CEM,
又∵∠ACBA=45°
∴∠MCE=45°
在△EDC和△EMC中,
,
∴△EDC≌△EMC(ASA)
∴EM=ED,
∵AM=AE+EM,
∴BD=DE+AE.
(3)
证明:如图,延长AE至点N,作EN=EG,
∵∠AEB =∠GEC,∠AEB =∠CEN,
∴∠GEC =∠CEN,
∴∠BEG =∠BEN,
在△BEG和△BEN中,
∴△BEG≌△BEN(SAS),
∴BN=BG,∠GBC =∠NBC,
∵∠GBC =45°-∠ABD,
∴∠ABN =90°-∠ABD,
∵∠BAN =90°-∠CAE,且∠ABD =∠CAE,
∴∠ABN =∠BAN,
∴AN=BN=BG,
∵AN=AE+EN=AE+EG
∴BG=AE+EG.
28.(1)分式是真分式.
(2)原式=
=
=
=
(3)原式=
=
=
=
=
∵分式的值为整数,
即=-2,-1,1,2
解得:x =-1,0,2,3
∴整数x的值为-1,0,2,3.
29.(1)证明:在图1中,有,,
∵,
∴;
(2)解:如图2所示,
∵,,
∴,
∵,,
∴,
∴,
∵,
∴.
(3)解①以M为交点“8字型”中,有,
以N为交点“8字型”中,有,
∴,
∵、分别平分和,
∴,,
∴,
∵,
∴;
②,其理由是:
∵,,
∴,,
以M为交点“8字型”中,有,
以N为交点“8字型”中,有,
∴,
.
∴,
∴.
学校:___________姓名:___________班级:___________学号:___________
一、单选题
1.以下列长度的各组线段为边,能组成三角形的是( )
A.2cm,4cm,6cm B.2cm,5cm,9cm
C.7cm,8cm,cm D.6cm,6cm,cm
2.科学家发现世界上最小的开花结果植物是澳大利亚的出水浮萍,这种植物的果实像一个微小的无花果,质量只有0.000000076克,0.000000076用科学记数法表示是( )
A. B. C. D.
3.在下列多项式的乘法中,可以用平方差公式计算的是( )
A. B.
C. D.
4.如图,在平面直角坐标系中,点A在第一象限,与x轴的夹角为,点P是x轴上一动点,若以P,O,A为顶点的三角形是等腰三角形,则满足条件的点P共有( )
A.2个 B.3个 C.4个 D.6个
5.小李同学制作了如图所示的卡片类、类、类各10张,其中、两类卡片都是正方形,类卡片是长方形.现要拼一个两边分别是和的大长方形,那么下列关于他所准备的类卡片的张数的说法中,正确的是( )
A.够用,剩余5张 B.够用,剩余1张
C.不够用,缺2张 D.不够用,缺3张
6.若2×8m×16m=229,则m的值是( )
A.3 B.4 C.5 D.6
7.如图,在△ABC中, AB的垂直平分线交AB于点D,AD=5cm,交边AC于点E,△BCE的周长等于18cm,则△ABC的周长等于( )
A.23cm B.25cm C.28cm D.30cm
8.如图,小虎用块高度都是的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(,),点C在上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离的长度为( )
A. B. C. D.
9.“绿水青山就是金山银山”.为改造太湖水质,某工程队对2400平方公里的水域进行水质净化,实际工作时每天的工作效率比原计划提高了20%,结果提前了40天完成任务.设实际每天净化的水域面积为x平方公里,则下列方程中正确的是( )
A. B.
C. D.
10.如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF,以下结论:①AD∥BC,②∠ACB=∠ADB,③∠ADC+∠ABD=90°,④∠ADB=45°﹣∠CDB,其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.分解因式: .
12.若,则p的值是 .
13.如图所示,在中,,直线,分别与边交于两点,则 .
14.已知的展开式中不含项,常数项是,则 .
15.若关于x的方程 无解,则m的值是 .
16.如图,于点,于点,,点从点出发以的速度向点运动(到达点停止运动),点从点出发沿着方向运动,、两点同时出发,同时停止运动,若与点、、所构成的三角形全等,则点运动的速度为 .
17.如图,在的边上取点,连接,平分,平分,若,的面积是2,的面积是6,则的长是 .
18.如图,在第1个中,,,往上取一点,延长到,使得;在上取一点,延长到,使得;…;按此作法进行下去,第个三角形中以为顶点的内角的度数为 .
三、解答题
19.完成下列各题
(1)化简; (2)分解因式.
20.(1)先化简,得求值:,其中.
(2)先化简,再求值:,其中.
21.解方程:
(1) (2)
22.如图,的顶点都在格点上,点A坐标为.
(1)将沿y轴正方向平移3个单位长度,得到,画出,并写出点的坐标;
(2)画出关于直线对称的,并写出点的坐标.
23.已知:如图,在四边形中,,.求证:.小明同学的证明过程如下框:
小明的证法是否正确?若正确,请在框内打“√”;若错误,请写出你的证明过程.
24.图①是一个长为,宽为的长方形,用剪刀沿图中虚线(对称轴)剪开.把它分成四块形状和大小都一样的小长方形,然后按图②拼成一个正方形.
(1)图②中间空白部分的面积是________(填、或).
(2)观察图②,请写出代数式、、之间的等量关系式.
(3)根据图②得到的关系式解答下列问题:若,,求的值.
25.如图,在中,,垂直平分,交于点F,交于点E,且,连接.
(1)求证:;
(2)若的周长为,,求的长.
26.某商场第一次购进一定数量的A,B两个款式的T恤,其中A款T恤一共花费1200元,B款T恤一共花费6000元,每件B款T恤的进价比每件A款T恤的进价高80元,且B款T恤的数量刚好是A款T恤数量的3倍.
(1)求第一次购进的A,B两款T恤的进价;
(2)第一批货卖完后,商场决定再购进一定数量的B款T恤,且进货量不超过60件,商场的销售情况如下:先按标价300元卖了15件,剩余的按标价打八折进行促销,若总利润不低于3220元,求第二次可购进B款T恤多少件.
27.如图1,等腰Rt△ABC中,∠BAC=90°,AB=AC,D,E分别是AC和BC上的动点,BD⊥AE,垂足为F.
(1)求证∠CAE=∠ABD;
(2)连接DE,满足∠AEB=∠DEC,求证:BD=DE+AE;
(3)点G在BD的延长线上,连接EG,满足∠AEB=∠GEC,试写出AE,EG,BG之间的数量关系,并证明.
28.阅读下列材料:通过小学的学习我们知道,分数可分为“真分数”和“假分数”.而假分数都可化为带分数,如:.我们定义:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.如:,这样的分式就是假分式;再如:,这样的分式就是真分式.类似的,“假分式”也可以化为“带分式”(即:整式与真分式的和的形式).
如:;
再如:.
解决下列问题:
(1)分式是________分式(填“真”或“假”);
(2)请将假分式化为带分式的形式;
(3)若分式的值为整数,求满足条件的整数x的值.
29.如图1,已知线段、相交于点O,连接、,则我们把形如这样的图形称为“8字型”.
(1)求证:.
(2)如图2所示,,则的度数为 .
(3)如图3,若和的平分线和相交于点P,且与,分别相交于点M,N.
①若,,求∠P的度数.
②若角平分线中角的关系改成“, ”,试直接写出与,之间存在的数量关系,并证明理由.
第1页 共4页 ◎ 第2页 共4页
参考答案
1.C
2.B
3.C
4.A
5.D
6.B
7.C
8.A
9.C
10.B
11.
12.
13.
14.
15.或
16.4或
17.8
18.
19.(1)解:
;
(2)解:
.
20.解:(1)
当时,原式.
(2)
当时,原式.
21.(1)解:方程两边同乘以得
,
解得:,
检验:当时,
,
是原方程的解;
(2)解:方程两边同乘以()得
,
解得:,
检验:当时,,
是原方程的解.
22.(1)解:如图所示:即为所求;点坐标为.
(2)如图所示:,即为所求,点的坐标为.
23.小明的证法错误;
证明:连接.
∵,∴,
又∵,∴,
为等腰三角形,
∴.
24.(1)解:由图形可知:空白部分的面积.
(2)解:由图②可知:大正方形面积=空白部分的面积+4个长方形面积,
∴;
(3)解:∵,
∴,
∵,,
∴,
∴.
25.(1)证明:垂直平分,
,
,,
垂直平分,
,
;
(2)解:的周长为,
,
,
,
,,
.
26.(1)解:设第一次购进的款恤的进价为元,则款恤的进价为元,
由题意得:,
解得:,
经检验,是原方程的解,且符合题意,
,
答:第一次购进的款恤的进价为120元,款恤的进价为200元;
(2)解:设第二次可购进款恤件,
由题意得:,
解得:,
为正整数,
或59或60,
答:第二次可购进款恤58件或59件或60件.
27.(1)
证明:∵BD⊥AF,
∴∠BFA=90°,
∵∠CAE+∠BAF=90°,∠ABD+∠BAF=90°
∴∠CAE=∠ABD.
(2)
证明:如图,作CM⊥AD于点C,CM交AE的延长线于点M
由①知,∠CAE=∠ABD
在△ABD和△CAM中,,
∴△ABD≌△CAM(ASA)
∴BD=AM,
∵∠AEB=∠CEM,
∴∠DEC=∠CEM,
又∵∠ACBA=45°
∴∠MCE=45°
在△EDC和△EMC中,
,
∴△EDC≌△EMC(ASA)
∴EM=ED,
∵AM=AE+EM,
∴BD=DE+AE.
(3)
证明:如图,延长AE至点N,作EN=EG,
∵∠AEB =∠GEC,∠AEB =∠CEN,
∴∠GEC =∠CEN,
∴∠BEG =∠BEN,
在△BEG和△BEN中,
∴△BEG≌△BEN(SAS),
∴BN=BG,∠GBC =∠NBC,
∵∠GBC =45°-∠ABD,
∴∠ABN =90°-∠ABD,
∵∠BAN =90°-∠CAE,且∠ABD =∠CAE,
∴∠ABN =∠BAN,
∴AN=BN=BG,
∵AN=AE+EN=AE+EG
∴BG=AE+EG.
28.(1)分式是真分式.
(2)原式=
=
=
=
(3)原式=
=
=
=
=
∵分式的值为整数,
即=-2,-1,1,2
解得:x =-1,0,2,3
∴整数x的值为-1,0,2,3.
29.(1)证明:在图1中,有,,
∵,
∴;
(2)解:如图2所示,
∵,,
∴,
∵,,
∴,
∴,
∵,
∴.
(3)解①以M为交点“8字型”中,有,
以N为交点“8字型”中,有,
∴,
∵、分别平分和,
∴,,
∴,
∵,
∴;
②,其理由是:
∵,,
∴,,
以M为交点“8字型”中,有,
以N为交点“8字型”中,有,
∴,
.
∴,
∴.
