2024-2025学年人教版五年级数学上册期末临考猜题卷 (含答案+解析)
文档属性
| 名称 | 2024-2025学年人教版五年级数学上册期末临考猜题卷 (含答案+解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-12 00:00:00 | ||
图片预览


文档简介
保密★启用前
2024-2025学年五年级上册期末临考猜题卷(人教版)
数学
考试范围:五上全册 考试时间:90分钟 分值:120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、认真读题,专心填写。(每空1分,共24分)
1.在横线上填“>”“<”或“=”。
0.16÷0.08 0.16×0.08 0.6×0.6 0.6+0.6
20.4×0.5 2.04×5 70 6.9×9.9
2.在3.1415926的小数部分的某一个或两个数位上加上表示循环节的点,将它变成循环小数,则得到的循环小数中最大的是 ,最小的是 。
3.把写成循环小数后,小数点后第35位上是 。
4.自由游戏时间。根据下面三种游戏中的描述,选择游戏 获胜的可能性最大。
5.在圆圈里填上“>”“<”或“=”。
①3.5÷0.93.5 ② 4.6÷0.024.6÷0.2 ③4.64.6×1.2
④3.6÷1.23.6 ⑤ 3.2÷0.13.2×10 ⑥ 83×0.8783
6.把一个平行四边形(如图)分成a、b、c三部分,已知c的面积比b多8平方厘米。平行四边形的面积是 平方厘米。
7. 文具店出售素描套装,包含1本素描本、4支铅笔、1个橡皮和1个素描板。其中1支铅笔a元,1本素描本的价格是1支铅笔价格的6倍,1个橡皮b元,1个素描板的价格是1个橡皮价格的5倍,购买套装比单独购买便宜(2a+b)元。素描套装 元,当a=1.5,b=2时,买这样一套素描套装一共要用 元。
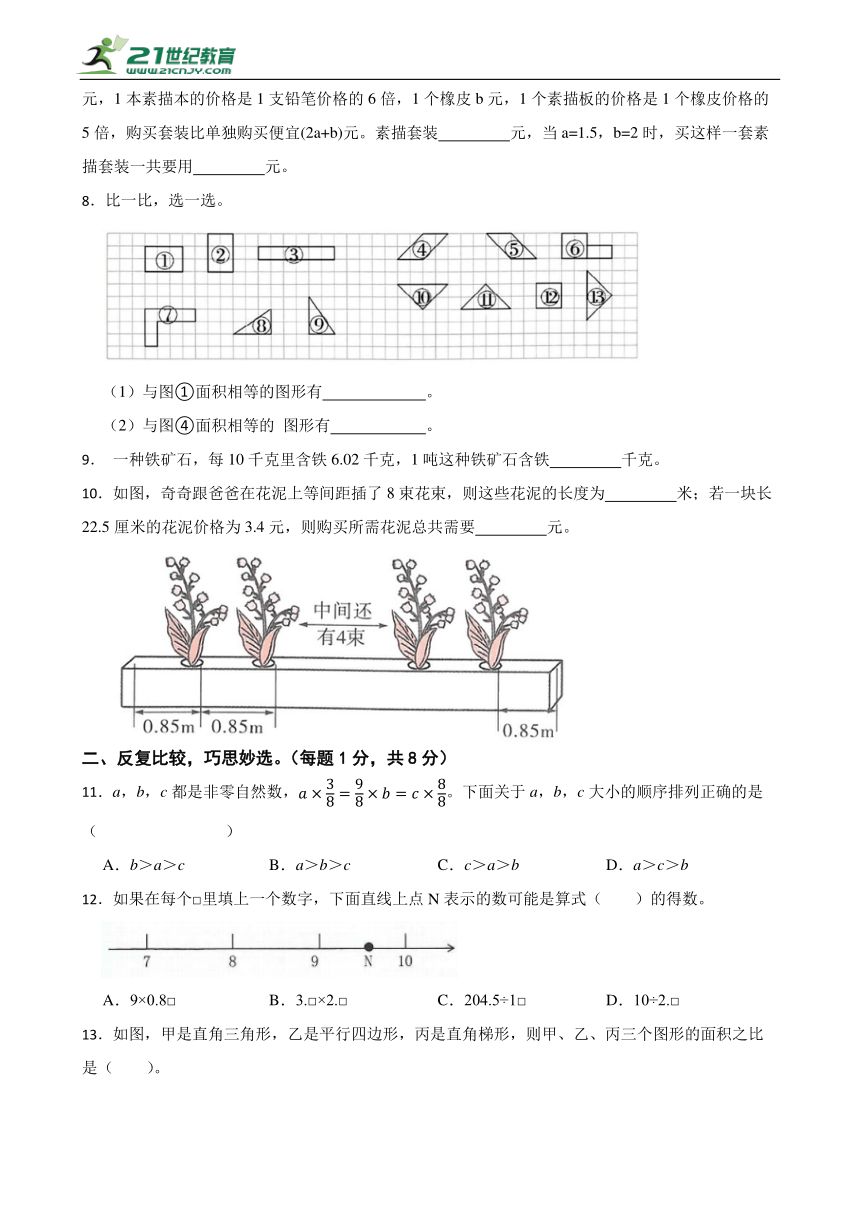
8.比一比,选一选。
(1)与图①面积相等的图形有 。
(2)与图④面积相等的 图形有 。
9. 一种铁矿石,每10千克里含铁6.02千克,1吨这种铁矿石含铁 千克。
10.如图,奇奇跟爸爸在花泥上等间距插了8束花束,则这些花泥的长度为 米;若一块长22.5厘米的花泥价格为3.4元,则购买所需花泥总共需要 元。
二、反复比较,巧思妙选。(每题1分,共8分)
11.a,b,c都是非零自然数,。下面关于a,b,c大小的顺序排列正确的是( )
A.b>a>c B.a>b>c C.c>a>b D.a>c>b
12.如果在每个□里填上一个数字,下面直线上点N表示的数可能是算式( )的得数。
A.9×0.8□ B.3.□×2.□ C.204.5÷1□ D.10÷2.□
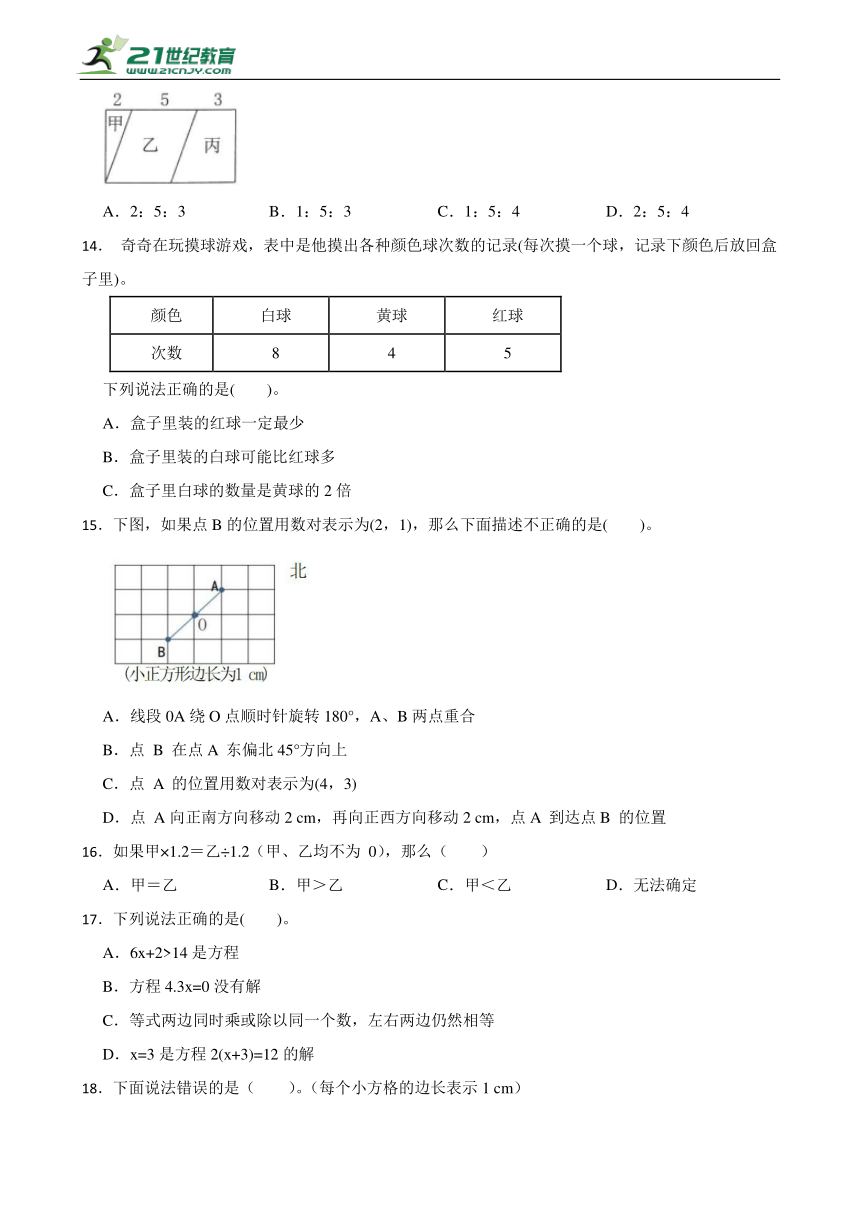
13.如图,甲是直角三角形,乙是平行四边形,丙是直角梯形,则甲、乙、丙三个图形的面积之比是( )。
A.2:5:3 B.1:5:3 C.1:5:4 D.2:5:4
14. 奇奇在玩摸球游戏,表中是他摸出各种颜色球次数的记录(每次摸一个球,记录下颜色后放回盒子里)。
颜色 白球 黄球 红球
次数 8 4 5
下列说法正确的是( )。
A.盒子里装的红球一定最少
B.盒子里装的白球可能比红球多
C.盒子里白球的数量是黄球的2倍
15.下图,如果点B的位置用数对表示为(2,1),那么下面描述不正确的是( )。
A.线段0A绕O点顺时针旋转180°,A、B两点重合
B.点 B 在点A 东偏北45°方向上
C.点 A 的位置用数对表示为(4,3)
D.点 A向正南方向移动2 cm,再向正西方向移动2 cm,点A 到达点B 的位置
16.如果甲×1.2=乙÷1.2(甲、乙均不为 0),那么( )
A.甲=乙 B.甲>乙 C.甲<乙 D.无法确定
17.下列说法正确的是( )。
A.6x+2>14是方程
B.方程4.3x=0没有解
C.等式两边同时乘或除以同一个数,左右两边仍然相等
D.x=3是方程2(x+3)=12的解
18.下面说法错误的是( )。(每个小方格的边长表示1 cm)
A.图②的面积等于图⑥的面积
B.图④的面积等于图⑤的面积
C.图①和图⑦可以拼成一个长方形
D.图③的面积是6 cm2
三、注意审题,合理计算。(共33分)
19.直接写出得数。
5-0.7= 3.5a+0.5la= 3.87x-1.1x= 12.09+7.9=
0.252= 5.6÷0.64= 4.12÷0.2= 1.8×6.55=
用竖式计算。(带★号的题目得数保留两位小数)
0.45×2.48= 3.36÷9.6= ★9.68÷5.2=
21.解方程。
50%x-33%x=34
x÷(1-40%)=3.6
22.脱式计算。 (能简算的要简算)
⑴9.6-5.98÷4.6×6.4 ⑵ 0.137×5.8+1.37×0.32+0.137
⑶1.08× (5.2+2.99÷2.3) ⑷9.27÷0.125÷80
四、动手操作,图形计算。(共11分)
23.同一时刻同一地点, 竿高和影长的变化如下表。
竿高 / 米 0 2 3 4 5 6 ……
影长 / 米 0 3.0 4.5 6.0 7.5 9.0 ……
(1)表中 随着 的变化而变化。如果用 x 表示竿高,用 y 表示影长,那么 y= 。竿高和影长成 比例。
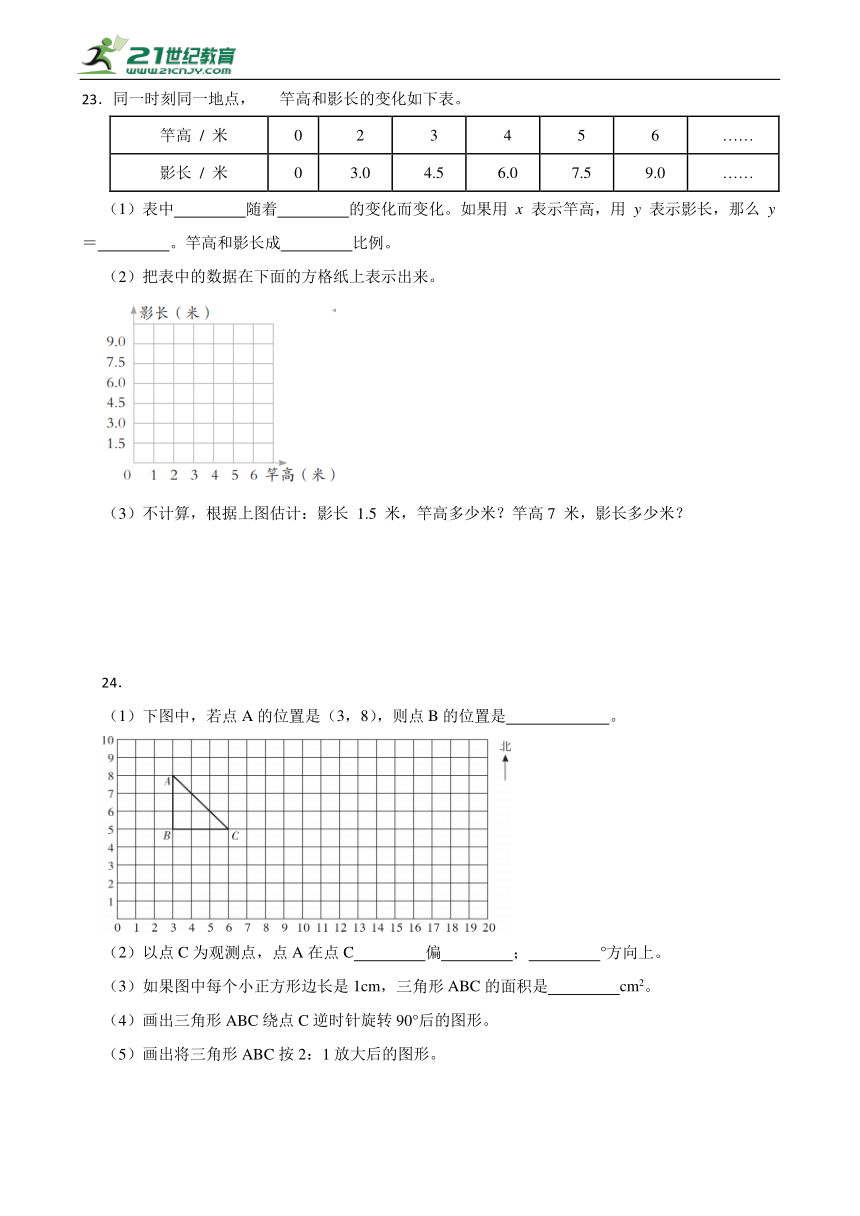
(2)把表中的数据在下面的方格纸上表示出来。
不计算,根据上图估计:影长 1.5 米,竿高多少米?竿高7 米,影长多少米?
24.
(1)下图中,若点A的位置是(3,8),则点B的位置是 。
(2)以点C为观测点,点A在点C 偏 ; °方向上。
(3)如果图中每个小正方形边长是1cm,三角形ABC的面积是 cm2。
(4)画出三角形ABC绕点C逆时针旋转90°后的图形。
(5)画出将三角形ABC按2:1放大后的图形。
五、走进生活,解决问题。(第28、29题各6分,其余每题4分,共24分)
25.如图,将一块四边形菜地分成一个梯形和一个三角形,梯形的上底6m,下底15m,高7m。
(1)梯形菜地的面积是多少平方米
(2)三角形菜地的面积是多少平方米
今年的上海,由于疫情,旅游业遭到了前所未有的困难。以上海科技馆为例,2022年2月参观人数达到195万人,今年2月份的人数不到去年的。今天2月有多少万人参观了上海科技馆 (用方程解)
27.坚持正确刷牙,保持口腔卫生能预防蛀牙。笑笑买了一支净含量为60克的儿童牙膏,她早晚各刷一次牙,平均每次刷牙用去1.25克牙膏。这支牙膏够笑笑用多少天?
28.某地自来水实行阶梯式收费标准,计费标准如下表:
月用水量(/户) 价格(元/)
10以下(包括10) 1.8
10~20(不包括10,包括20) 2.4
20以上 3.2
(1)小明家7月份用水9.8,应付水费多少钱?
(2)小明家8月份付水费31.20元,他家8月份用了多少立方米水?
29.甲、乙两车分别从A、B两地同时出发,相向而行.出发时,甲、乙的速度之比是5:4,相遇后甲的速度减少20%,乙的速度增加20%.这样当甲到达B地时,乙离A地还有10千米.那么A、B两地相距多少千米?
答案解析部分
1.>;<;=;>
解:因为0.08<1,所以0.16÷0.08>0.16,而0.16×0.08<0.16,因此0.16÷0.08>0.16×0.08;
因为0.6<1,所以0.6×0.6<0.6,因为0.6+0.6=0.6×2,2>1,所以0.6×2>0.6,因此0.6×0.6<0.6+0.6;
因为20.4×0.5=(20.4÷10)×(0.5×10)=2.04×5,所以20.4×0.5=2.04×5;
6.9×10=69<70,因为9.9<10,所以6.9×9.9<6.9×10,因此70>6.9×9.9。
故答案为:>;<;=;>。
商的变化规律:一个数除以一个大于1的数,商小于它本身;一个数除以一个小于1的数,商大于它本身。
积的变化规律:①一个数乘一个大于1的数,积大于它本身;一个数乘一个小于1的数,积小于它本身;一个数乘一个等于1的数,积等于它本身;
②一个因数扩大另一个因数缩小相同的倍数(0除外),积不变。
积的估算:找其中一个最接近因数的整十、整百、整千等数进行计算,估算结果如果因数是估大那么结果就比准确值大,如果因数是估小那么结果就比准确值小。
2.;
解:得到的循环小数中最大的是,最小的是。
故答案为:;。
小数比较大小,先比较整数部分,整数部分大的数就大,如果整数部分相同,再比较小数部分十分位上的数,十分位上的数大的就大,如果十分位上的数相同就比较百分位上的数······直到比出大小为止。
3.5
解:=0.142857142857……
35÷6=5……5
所以小数点后第35位上是5。
故答案为:5。
先用分子除以分母将分数转化成小数,发现小数是以142857六位数为循环节的循环小数,所以用所求位数÷6=几组循环节……余数,余数是几就是循环节中的第几个数字,没有余数就是循环节中的最后一个数字,据此可以解答。
4.②
解:根据题意,可得
图①中的占比为:
图②中的的占比为:
图③中的的占比为:0
因为
所以,选择游戏②获胜的可能性最大。
故答案为:②
观察图①,可知的数量为1,占整个图中动物数量的;图②中的数量为6个,占整个图中水果的;图③中的数量为0,然后根据其各自的占比,占比大的可能性就大。
5.①3.5÷0.93.5 ② 4.6÷0.024.6÷0.2 ③4.64.6×1.2
④3.6÷1.23.6 ⑤ 3.2÷0.13.2×10 ⑥ 83×0.8783
解:①因为0.9<1,所以3.5÷0.9 3.5;
②因为0.02<0.2<1,所以4.6÷0.02 4.6÷0.2;
③因为1.2>1,所以4.6 4.6×1.2;
④因为1.2>1,所以3.6÷1.23.6;
⑤3.2÷0.13.2×10;
⑥ 因为0.87<1,所以83×0.8783。
故答案为:; ; ;;;。
一个数(0除外)乘一个小于1的数,积小于原数;一个数(0除外)乘一个大于1的数,积大于原数;一个数(0除外)除以一个大于1的数,商小于原数;一个数(0除外)除以一个小于1的数,商大于原数;一个数除以0.1,相当于这个数乘10;据此解答。
6.80
解:设平行四边形的高是x厘米。
6x÷2-4x÷2=8
3x-2x=8
x=8
(4+6)×8
=10×8
=80(平方厘米)。
故答案为:80。
设平行四边形的高是x厘米。依据c的底×高÷2-b的底×高÷2=8平方厘米,列方程,解方程求出x=8,平行四边形的面积=底×高;其中,底=4+6=10厘米。
7.8a+5b;22
解:根据题意,可得
(1)单独购买素描的总价格为:6a+4a+b+5b=10a+6b
购买素描套装的价格为:10a+6b-(2a+b)=8a+5b
(2)将a=1.5,b=2代入8a+5b,可得
8×1.5+5×2
=12+10
=22(元)
故答案为:8a+5b;22
(1)根据“ 1个橡皮b元,1个素描板的价格是1个橡皮价格的5倍 ”,可知,1个素描板的额价格为5b;根据“1支铅笔a元,1本素描本的价格是1支铅笔价格的6倍”,可知一本素描本的价格是6a;因为素描套装包含1本素描本、4支铅笔、1个橡皮和1个素描板,所以单独购买素描的总价格等于6a+4a+b+5b=10a+6b;根据“ 购买套装比单独购买便宜(2a+b)元 ”,可知,购买素描套装的价格为:10a+6b-(2a+b)
(2)将a和b的值代入(1)中的式子,即可求解
8.(1)②③⑥⑦
(2)⑤⑩
解:图①的面积3×2=6;图②的面积2×3=6;图③的面积4+2=6;
图④的面积2×2=4;图⑤的面积2×2=4;图⑥的面积4+2=6;
图⑦的面积3+3=6;图⑧的面积3×2÷2=3;图⑨的面积2×3÷2=3;
图⑩的面积4×2÷2=4;图 的面积4×2÷2=4;图 的面积2×2=4;
图 的面积4×2÷2=4;
(1)与图①面积相等的图形有 ②③⑥⑦ ;
(2)与图④面积相等的 图形有 ⑤⑩
故答案为:(1) ②③⑥⑦ ;(2)⑤⑩ 。
长方形面积=长×宽,正方形面积=边长×边长,平行四边形面积=底×高,三角形面积=底×高÷2。
9.602
解:1吨=1000千克,
1000÷10×6.02
=100×6.02
=602(千克)
故答案为:602。
根据1吨=1000千克,已知每10千克里含铁6.02千克,要求1吨这种铁矿石含铁多少千克,就是求1吨里面有几个10千克,就有几个6.02千克,据此列式解答。
10.7.65;115.6
解:8+1=9(个)
9×0.85=7.65(米)
7.65÷0.225×3.4=115.6(元)
故答案为:7.65;115.6。
根据题图可知此题为两端都不栽的植树问题,则间隔数=棵数+1,8束花束有间隔数是9个,再根据总长度=间隔数×间距计算;用总长÷一块花泥的长度=块数,块数×单价=总价。
11.D
解:设等式:根据题意,设(k为常数,k>0,因为a, b, c都是非零自然数)。
求解a:由,得到。
求解b:由,得到。
求解c:由,得到。
比较大小:比较得到,即。
因此,正确的大小顺序为a > c > b。
故答案为:D。
首先,根据题目给定的等式关系,可以通过代数变形找到a, b, c之间的具体数值关系。这一步骤的关键在于利用等式两边相等的性质,将未知数表示成已知数的形式,从而得到a, b, c的表达式。然后,通过比较a, b, c的大小关系,确定正确的选项。
12.B
解:9A:9×0.8□<9,不是N表示的数;
B:3.□×2.□,积的范围在6到12之间,可能是N表示的数;
C:204.5÷1□>10,不是N表示的数;
D:10÷2.□<5,不是N不是的数。
故答案为:B。
根据小数乘除法的计算方法判断出每个算式得数的范围,然后选择得数可能大于9小于10的算式即可。
13.C
设三角形、平行四边形和梯形的高为1,则
三角形面积:2×1÷2=1
平行四边形面积:5×1=5
梯形面积:2+5+3-5=5
(5+3)×1÷2=4
故,甲、乙、丙三个图形面积的比是1:5:4
故答案为:C
由于这三个图形的高相等,设这三个图形的高为1,根据相应的面积公式求出它们的面积,再求它们的比。
14.B
解:A:摸到红球的次数最少不能说明盒子里装的红球一定最少;
B:摸到白球的次数比红球多,子里装的白球可能比红球多;
C:摸到的白球的数量是黄球的2倍,盒子里白球的数量不一定是黄球的2倍。
故答案为:B。
摸到的球的颜色情况不能代表盒子里装的球的颜色情况。
15.B
解:A:题中每个小正方形相同,故OA长度等于OB,点O为线段AB的中点,所以线段OA绕O点顺时针旋转180°,A、B两点重合;
B:点B在点A的左下方,且分别位于边长2cm的正方形两个相对的顶点上,正方形每个角的一半为45°,所以点B在点A西偏南45°方向上;
C:题干说点B的位置用数对表示为(2,1),说明是以最大长方形左下方的顶点为原点O,水平方向为x轴,竖直方向为y轴,建立坐标系,A点在顶点O的右方4个格子,上方3个格子,故点A的位置用数对表示为(4,3);
D:已经推断出A点坐标为(4,3),向正南方向移动2cm,即向下移动2个格子,坐标变成(2,3),再向正西方向移动2cm,即向左移动2个格子,坐标变成(2,1),正好对应点B的位置,所以点 A向正南方向移动2 cm,再向正西方向移动2 cm,点A 到达点B 的位置。
故答案为:B。
将一条线段AB从中点O截断,使OA绕其端点O旋转180°,OA与OB重合;
在平面图上通常确定的方位是:上北下南、左西右东;
如果一个点在平面直角坐标系中向右移动, 其x坐标会增加; 向上移动, 其y坐标会增加。
16.C
解:1.2>1,所以甲×1.2>甲,乙÷1.2<乙,而甲×1.2=乙÷1.2,所以甲<乙。
故答案为:C。
一个非0数乘比1大的数,所得的结果比这个数大;一个非0数除以比1大的数,所得的结果比这个数小。据此作答即可。
17.D
解:A.6x+2>14,是含有未知数的不等式,不是方程,错误;
B.方程4.3x=0的解是x=0,错误;
C.等式两边同时乘或除以同一个不为0的数,左右两边仍然相等,错误;
D.2×(3+3)=12,所以x=3是方程2(x+3)=12的解,正确。
故答案为:D
根据方程的定义、等式的基本性质、方程的解,逐项判断即可。
18.A
解:图①的面积是:5×2÷2=5,
图②的面积是:4×2=8,
图③的面积是:3+3=6,
图④的面积是:(2+4)×4÷2=12,
图⑤的面积是:2×6=12;
图⑥的面积是:3×3=9,
图⑦的面积是:4×5-5×2÷2=20-5=15,
说法错误的是图②的面积等于图⑥的面积
故答案为:A。
三角形面积=底×高÷2,长方形面积=长×宽,平行四边形面积=底×高,梯形面积=(上底+下底)×高÷2。
19.
5-0.7=4.3 3.5a+0.5la=4.01a 3.87x-1.1x=2.77x 12.09+7.9=19.9
0.252=0.0625 5.6÷0.64=8.75 4.12÷0.2=20.6 1.8×6.55=11.79
小数乘小数,先按照整数乘法去乘,再看因数中一共有几位小数,就从积的右边起数出几位点上小数点;除数是小数的小数除法,先移动除数的小数点,使它变成整数;除数的小数点向右移动几位,被除数的小数点也向右移动几位(位数不够的,在被除数的末尾用“0”补足),然后按照除数是整数的小数除法进行计算;小数加、减法,先把小数点对齐再计算;含有字母的式子求值,可根据小数的运算律计算。
20.解:0.45×2.48=1.116
3.36÷9.6=0.35
9.68÷5.2≈1.86
小数乘法计算方法:先按整数乘法算出积,再点小数点;点小数点时,看因数中一共有几位小数,就从积的右边起数出几位,点上小数点;
一个数除以小数,先移动除数的小数点,使它变成整数;除数的小数点向右移动几位,被除数的小数点也向右移动几位;位数不够时,在被除数的末尾用0补足;最后按照除数是整数的除法进行计算;
求一个小数的近似数,先看要求保留到那一位,然后再向后多看一位,把多看的这一位数四舍五入。
21.
19-x=13
解:19-x+x=13+x
13+x=19
13+x-13=19-13
x=6
x÷=6÷
x=16 x-x=
解:x=
x÷=÷
x=2
x÷20%=×2.4
解:x÷20%=2.1
x÷20%×20%=2.1×20%
x=0.42
x+x=7.8
解:x=7.8
x÷=7.8÷
x=6.5
x÷=14
解:x÷×=14×
x=8
x÷=8÷
x= 50%x-33%x=34
解:17%x=34
17%x÷17%=34÷17%
x=200
75%x-x=15
解:0.25x=15
0.25x÷0.25=15÷0.25
x=60
x÷(1-40%)=3.6
解:x÷60%=3.6
x÷60%×60%=3.6×60%
x=2.16
5x-3×=
解:5x-=
5x-+=+
5x=
5x÷5=÷5
x=
等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等;等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
解含有百分数的方程,需要先将百分数化为分数或小数,再利用等式的性质来求解。
22.解:⑴9.6-5.98÷4.6×6.4
=9.6-1.3×6.4
=9.6-8.32
=1.28
⑵ 0.137×5.8+1.37×0.32+0.137
=0.137×5.8+0.137×10×0.32+0.137
=0.137×(5.8+10×0.32+1)
=0.137×10
=1.37
⑶1.08× (5.2+2.99÷2.3)
=1.08× (5.2+1.3)
=1.08×6.5
=7.02
⑷9.27÷0.125÷80
=9.27÷(0.125×80)
=9.27÷10
=0.927
(1)按顺序计算,首先计算除法和乘法,然后计算减法即可;
(2)首先将1.37写成0.137×10,然后根据乘法分配律得到0.137×(5.8+10×0.32+1),最后按顺序计算即可;
(3)按顺序计算,首先计算小括号内的除法和加法,然后计算乘法即可;
(4)首先根据乘法结合律,得到9.27÷(0.125×80),然后先计算小括号内的乘法,再计算除法即可。
23.(1)影长;竿高;1.5x;正
(2)
(3)解:影长1.5米,竿高 1米;竿高 7米,影长 10.5米。
解:(1)表中影长随着竿高的变化而变化,y=1.5x,即y÷x=1.5,所以成正比例;
故答案为:(1)影长;竿高;1.5x;正。
(1)观察表格可知,竿高随着影长的增加而增加,且影长是竿高的1.5倍,据此写出关系式,两个相关联的量,如果比值一定,那么成正比例,影长与竿高的比值为1.5(一定),所以成正比例;
(2)根据描点法,先依次找出各点,然后顺序把各点连起来即可;
(3)根据图示,竿高与影长的关系是一条直线,当影长是1.5米时,竿高是1米;当竿高是7米时,影长是10.5米。
24.(1)(3,5)
(2)西;北;45
(3)4.5
(4)
(5)
解:(1)点B在第3列,第5行,所以点B的位置是:(3,5);
(2)三角形ABC是一个等腰直角三角形,ACB=45°,根据图上的方向标可知,点A在点C的西偏北45°方向上;
(3)332=4.5( cm2 );
故答案为:(1)(3,5);(2)西;北;45;(3)4.5。
(1)数对表示位置时,前一个数字表示列,后一个数字表示行;
(2)西偏北45 ° 是从正西方向向正北方向偏移45 ° ;
(3)三角形的面积=底高2;
(4)逆时针旋转90°:先给三角形的三个顶点分别表上字母A、B、C,然后将线段AC和线段BC绕点C分别逆时针旋转90°,得到线段A′C和B′C,最后将点A′和B′连在一起;
(5) 将图形按2:1放大:将三角形的两条直角边放大至32=6格,然后将两条直角边的另一顶点相连,画出底为6格、高为6格的三角形。
25.(1)解:(6+15)×7÷2
=21×7÷2
=147÷2
=73.5(平方米)
答:梯形菜地的面积是73.5平方米。
(2)解:15×(9-7)÷2
=15×2÷2
=15(平方米)
答:三角形菜地的面积是15平方米。
(1)梯形面积=(上底+下底)×高÷2,根据公式计算梯形面积;
(2)三角形面积=底×高÷2,三角形底是15米,所在的高是(9-7)米,由此计算面积。
26.解:设今天2月有x万人参观了上海科技馆。
8x=195
8x÷8=195÷8
x=24.375
答:今天2月有24.375万人参观了上海科技馆。
设今天2月有x万人参观了上海科技馆。依据等量关系:8×今天2月参观上海科技馆的人数= 2022年2月参观上海科技馆的人数,列方程,解方程。
27.解:60÷(1.25×2)
=60÷2.5
=24(天)
答:这支牙膏够笑笑用24天。
这支牙膏够笑笑用的天数=这支牙膏的总质量÷平均每天用的质量;其中,平均每天用的质量=一天早晚两次用掉的质量和。
28.(1)解:9.8×1.8=17.64(元)
答: 小明家7月份应付水费17.64元
(2)解:第一段费用:10×1.8=18(元)
第二段费用:31.2-18=13.2(元)
用水量:13.2÷2.4=5.5(吨)
小明家8月份用水量:10+5.5=15.5(吨)
答:小明家8月份用水量15.5吨。
分段计费问题,
(1)根据单价乘以数量=总价直接计算。
(2)第一段费用18元,第二段费用24,两段总费用42元,故8月份用水量不超过20吨。用总价除以单价=用水量。
29.解:两车相遇时甲走了全程的 ,乙走了全程的;
相遇后甲乙两车的速度比:
甲到达B地时,乙走了全程的:
与A地的距离:
则A、B两地的距离:
(千米)
答:A、B两地相距450千米。
设A、B两地的距离这两个未知数为x千米,利用速度比和相遇后的速度变化来建立方程,解方程即可。
2024-2025学年五年级上册期末临考猜题卷(人教版)
数学
考试范围:五上全册 考试时间:90分钟 分值:120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、认真读题,专心填写。(每空1分,共24分)
1.在横线上填“>”“<”或“=”。
0.16÷0.08 0.16×0.08 0.6×0.6 0.6+0.6
20.4×0.5 2.04×5 70 6.9×9.9
2.在3.1415926的小数部分的某一个或两个数位上加上表示循环节的点,将它变成循环小数,则得到的循环小数中最大的是 ,最小的是 。
3.把写成循环小数后,小数点后第35位上是 。
4.自由游戏时间。根据下面三种游戏中的描述,选择游戏 获胜的可能性最大。
5.在圆圈里填上“>”“<”或“=”。
①3.5÷0.93.5 ② 4.6÷0.024.6÷0.2 ③4.64.6×1.2
④3.6÷1.23.6 ⑤ 3.2÷0.13.2×10 ⑥ 83×0.8783
6.把一个平行四边形(如图)分成a、b、c三部分,已知c的面积比b多8平方厘米。平行四边形的面积是 平方厘米。
7. 文具店出售素描套装,包含1本素描本、4支铅笔、1个橡皮和1个素描板。其中1支铅笔a元,1本素描本的价格是1支铅笔价格的6倍,1个橡皮b元,1个素描板的价格是1个橡皮价格的5倍,购买套装比单独购买便宜(2a+b)元。素描套装 元,当a=1.5,b=2时,买这样一套素描套装一共要用 元。
8.比一比,选一选。
(1)与图①面积相等的图形有 。
(2)与图④面积相等的 图形有 。
9. 一种铁矿石,每10千克里含铁6.02千克,1吨这种铁矿石含铁 千克。
10.如图,奇奇跟爸爸在花泥上等间距插了8束花束,则这些花泥的长度为 米;若一块长22.5厘米的花泥价格为3.4元,则购买所需花泥总共需要 元。
二、反复比较,巧思妙选。(每题1分,共8分)
11.a,b,c都是非零自然数,。下面关于a,b,c大小的顺序排列正确的是( )
A.b>a>c B.a>b>c C.c>a>b D.a>c>b
12.如果在每个□里填上一个数字,下面直线上点N表示的数可能是算式( )的得数。
A.9×0.8□ B.3.□×2.□ C.204.5÷1□ D.10÷2.□
13.如图,甲是直角三角形,乙是平行四边形,丙是直角梯形,则甲、乙、丙三个图形的面积之比是( )。
A.2:5:3 B.1:5:3 C.1:5:4 D.2:5:4
14. 奇奇在玩摸球游戏,表中是他摸出各种颜色球次数的记录(每次摸一个球,记录下颜色后放回盒子里)。
颜色 白球 黄球 红球
次数 8 4 5
下列说法正确的是( )。
A.盒子里装的红球一定最少
B.盒子里装的白球可能比红球多
C.盒子里白球的数量是黄球的2倍
15.下图,如果点B的位置用数对表示为(2,1),那么下面描述不正确的是( )。
A.线段0A绕O点顺时针旋转180°,A、B两点重合
B.点 B 在点A 东偏北45°方向上
C.点 A 的位置用数对表示为(4,3)
D.点 A向正南方向移动2 cm,再向正西方向移动2 cm,点A 到达点B 的位置
16.如果甲×1.2=乙÷1.2(甲、乙均不为 0),那么( )
A.甲=乙 B.甲>乙 C.甲<乙 D.无法确定
17.下列说法正确的是( )。
A.6x+2>14是方程
B.方程4.3x=0没有解
C.等式两边同时乘或除以同一个数,左右两边仍然相等
D.x=3是方程2(x+3)=12的解
18.下面说法错误的是( )。(每个小方格的边长表示1 cm)
A.图②的面积等于图⑥的面积
B.图④的面积等于图⑤的面积
C.图①和图⑦可以拼成一个长方形
D.图③的面积是6 cm2
三、注意审题,合理计算。(共33分)
19.直接写出得数。
5-0.7= 3.5a+0.5la= 3.87x-1.1x= 12.09+7.9=
0.252= 5.6÷0.64= 4.12÷0.2= 1.8×6.55=
用竖式计算。(带★号的题目得数保留两位小数)
0.45×2.48= 3.36÷9.6= ★9.68÷5.2=
21.解方程。
50%x-33%x=34
x÷(1-40%)=3.6
22.脱式计算。 (能简算的要简算)
⑴9.6-5.98÷4.6×6.4 ⑵ 0.137×5.8+1.37×0.32+0.137
⑶1.08× (5.2+2.99÷2.3) ⑷9.27÷0.125÷80
四、动手操作,图形计算。(共11分)
23.同一时刻同一地点, 竿高和影长的变化如下表。
竿高 / 米 0 2 3 4 5 6 ……
影长 / 米 0 3.0 4.5 6.0 7.5 9.0 ……
(1)表中 随着 的变化而变化。如果用 x 表示竿高,用 y 表示影长,那么 y= 。竿高和影长成 比例。
(2)把表中的数据在下面的方格纸上表示出来。
不计算,根据上图估计:影长 1.5 米,竿高多少米?竿高7 米,影长多少米?
24.
(1)下图中,若点A的位置是(3,8),则点B的位置是 。
(2)以点C为观测点,点A在点C 偏 ; °方向上。
(3)如果图中每个小正方形边长是1cm,三角形ABC的面积是 cm2。
(4)画出三角形ABC绕点C逆时针旋转90°后的图形。
(5)画出将三角形ABC按2:1放大后的图形。
五、走进生活,解决问题。(第28、29题各6分,其余每题4分,共24分)
25.如图,将一块四边形菜地分成一个梯形和一个三角形,梯形的上底6m,下底15m,高7m。
(1)梯形菜地的面积是多少平方米
(2)三角形菜地的面积是多少平方米
今年的上海,由于疫情,旅游业遭到了前所未有的困难。以上海科技馆为例,2022年2月参观人数达到195万人,今年2月份的人数不到去年的。今天2月有多少万人参观了上海科技馆 (用方程解)
27.坚持正确刷牙,保持口腔卫生能预防蛀牙。笑笑买了一支净含量为60克的儿童牙膏,她早晚各刷一次牙,平均每次刷牙用去1.25克牙膏。这支牙膏够笑笑用多少天?
28.某地自来水实行阶梯式收费标准,计费标准如下表:
月用水量(/户) 价格(元/)
10以下(包括10) 1.8
10~20(不包括10,包括20) 2.4
20以上 3.2
(1)小明家7月份用水9.8,应付水费多少钱?
(2)小明家8月份付水费31.20元,他家8月份用了多少立方米水?
29.甲、乙两车分别从A、B两地同时出发,相向而行.出发时,甲、乙的速度之比是5:4,相遇后甲的速度减少20%,乙的速度增加20%.这样当甲到达B地时,乙离A地还有10千米.那么A、B两地相距多少千米?
答案解析部分
1.>;<;=;>
解:因为0.08<1,所以0.16÷0.08>0.16,而0.16×0.08<0.16,因此0.16÷0.08>0.16×0.08;
因为0.6<1,所以0.6×0.6<0.6,因为0.6+0.6=0.6×2,2>1,所以0.6×2>0.6,因此0.6×0.6<0.6+0.6;
因为20.4×0.5=(20.4÷10)×(0.5×10)=2.04×5,所以20.4×0.5=2.04×5;
6.9×10=69<70,因为9.9<10,所以6.9×9.9<6.9×10,因此70>6.9×9.9。
故答案为:>;<;=;>。
商的变化规律:一个数除以一个大于1的数,商小于它本身;一个数除以一个小于1的数,商大于它本身。
积的变化规律:①一个数乘一个大于1的数,积大于它本身;一个数乘一个小于1的数,积小于它本身;一个数乘一个等于1的数,积等于它本身;
②一个因数扩大另一个因数缩小相同的倍数(0除外),积不变。
积的估算:找其中一个最接近因数的整十、整百、整千等数进行计算,估算结果如果因数是估大那么结果就比准确值大,如果因数是估小那么结果就比准确值小。
2.;
解:得到的循环小数中最大的是,最小的是。
故答案为:;。
小数比较大小,先比较整数部分,整数部分大的数就大,如果整数部分相同,再比较小数部分十分位上的数,十分位上的数大的就大,如果十分位上的数相同就比较百分位上的数······直到比出大小为止。
3.5
解:=0.142857142857……
35÷6=5……5
所以小数点后第35位上是5。
故答案为:5。
先用分子除以分母将分数转化成小数,发现小数是以142857六位数为循环节的循环小数,所以用所求位数÷6=几组循环节……余数,余数是几就是循环节中的第几个数字,没有余数就是循环节中的最后一个数字,据此可以解答。
4.②
解:根据题意,可得
图①中的占比为:
图②中的的占比为:
图③中的的占比为:0
因为
所以,选择游戏②获胜的可能性最大。
故答案为:②
观察图①,可知的数量为1,占整个图中动物数量的;图②中的数量为6个,占整个图中水果的;图③中的数量为0,然后根据其各自的占比,占比大的可能性就大。
5.①3.5÷0.93.5 ② 4.6÷0.024.6÷0.2 ③4.64.6×1.2
④3.6÷1.23.6 ⑤ 3.2÷0.13.2×10 ⑥ 83×0.8783
解:①因为0.9<1,所以3.5÷0.9 3.5;
②因为0.02<0.2<1,所以4.6÷0.02 4.6÷0.2;
③因为1.2>1,所以4.6 4.6×1.2;
④因为1.2>1,所以3.6÷1.23.6;
⑤3.2÷0.13.2×10;
⑥ 因为0.87<1,所以83×0.8783。
故答案为:; ; ;;;。
一个数(0除外)乘一个小于1的数,积小于原数;一个数(0除外)乘一个大于1的数,积大于原数;一个数(0除外)除以一个大于1的数,商小于原数;一个数(0除外)除以一个小于1的数,商大于原数;一个数除以0.1,相当于这个数乘10;据此解答。
6.80
解:设平行四边形的高是x厘米。
6x÷2-4x÷2=8
3x-2x=8
x=8
(4+6)×8
=10×8
=80(平方厘米)。
故答案为:80。
设平行四边形的高是x厘米。依据c的底×高÷2-b的底×高÷2=8平方厘米,列方程,解方程求出x=8,平行四边形的面积=底×高;其中,底=4+6=10厘米。
7.8a+5b;22
解:根据题意,可得
(1)单独购买素描的总价格为:6a+4a+b+5b=10a+6b
购买素描套装的价格为:10a+6b-(2a+b)=8a+5b
(2)将a=1.5,b=2代入8a+5b,可得
8×1.5+5×2
=12+10
=22(元)
故答案为:8a+5b;22
(1)根据“ 1个橡皮b元,1个素描板的价格是1个橡皮价格的5倍 ”,可知,1个素描板的额价格为5b;根据“1支铅笔a元,1本素描本的价格是1支铅笔价格的6倍”,可知一本素描本的价格是6a;因为素描套装包含1本素描本、4支铅笔、1个橡皮和1个素描板,所以单独购买素描的总价格等于6a+4a+b+5b=10a+6b;根据“ 购买套装比单独购买便宜(2a+b)元 ”,可知,购买素描套装的价格为:10a+6b-(2a+b)
(2)将a和b的值代入(1)中的式子,即可求解
8.(1)②③⑥⑦
(2)⑤⑩
解:图①的面积3×2=6;图②的面积2×3=6;图③的面积4+2=6;
图④的面积2×2=4;图⑤的面积2×2=4;图⑥的面积4+2=6;
图⑦的面积3+3=6;图⑧的面积3×2÷2=3;图⑨的面积2×3÷2=3;
图⑩的面积4×2÷2=4;图 的面积4×2÷2=4;图 的面积2×2=4;
图 的面积4×2÷2=4;
(1)与图①面积相等的图形有 ②③⑥⑦ ;
(2)与图④面积相等的 图形有 ⑤⑩
故答案为:(1) ②③⑥⑦ ;(2)⑤⑩ 。
长方形面积=长×宽,正方形面积=边长×边长,平行四边形面积=底×高,三角形面积=底×高÷2。
9.602
解:1吨=1000千克,
1000÷10×6.02
=100×6.02
=602(千克)
故答案为:602。
根据1吨=1000千克,已知每10千克里含铁6.02千克,要求1吨这种铁矿石含铁多少千克,就是求1吨里面有几个10千克,就有几个6.02千克,据此列式解答。
10.7.65;115.6
解:8+1=9(个)
9×0.85=7.65(米)
7.65÷0.225×3.4=115.6(元)
故答案为:7.65;115.6。
根据题图可知此题为两端都不栽的植树问题,则间隔数=棵数+1,8束花束有间隔数是9个,再根据总长度=间隔数×间距计算;用总长÷一块花泥的长度=块数,块数×单价=总价。
11.D
解:设等式:根据题意,设(k为常数,k>0,因为a, b, c都是非零自然数)。
求解a:由,得到。
求解b:由,得到。
求解c:由,得到。
比较大小:比较得到,即。
因此,正确的大小顺序为a > c > b。
故答案为:D。
首先,根据题目给定的等式关系,可以通过代数变形找到a, b, c之间的具体数值关系。这一步骤的关键在于利用等式两边相等的性质,将未知数表示成已知数的形式,从而得到a, b, c的表达式。然后,通过比较a, b, c的大小关系,确定正确的选项。
12.B
解:9
B:3.□×2.□,积的范围在6到12之间,可能是N表示的数;
C:204.5÷1□>10,不是N表示的数;
D:10÷2.□<5,不是N不是的数。
故答案为:B。
根据小数乘除法的计算方法判断出每个算式得数的范围,然后选择得数可能大于9小于10的算式即可。
13.C
设三角形、平行四边形和梯形的高为1,则
三角形面积:2×1÷2=1
平行四边形面积:5×1=5
梯形面积:2+5+3-5=5
(5+3)×1÷2=4
故,甲、乙、丙三个图形面积的比是1:5:4
故答案为:C
由于这三个图形的高相等,设这三个图形的高为1,根据相应的面积公式求出它们的面积,再求它们的比。
14.B
解:A:摸到红球的次数最少不能说明盒子里装的红球一定最少;
B:摸到白球的次数比红球多,子里装的白球可能比红球多;
C:摸到的白球的数量是黄球的2倍,盒子里白球的数量不一定是黄球的2倍。
故答案为:B。
摸到的球的颜色情况不能代表盒子里装的球的颜色情况。
15.B
解:A:题中每个小正方形相同,故OA长度等于OB,点O为线段AB的中点,所以线段OA绕O点顺时针旋转180°,A、B两点重合;
B:点B在点A的左下方,且分别位于边长2cm的正方形两个相对的顶点上,正方形每个角的一半为45°,所以点B在点A西偏南45°方向上;
C:题干说点B的位置用数对表示为(2,1),说明是以最大长方形左下方的顶点为原点O,水平方向为x轴,竖直方向为y轴,建立坐标系,A点在顶点O的右方4个格子,上方3个格子,故点A的位置用数对表示为(4,3);
D:已经推断出A点坐标为(4,3),向正南方向移动2cm,即向下移动2个格子,坐标变成(2,3),再向正西方向移动2cm,即向左移动2个格子,坐标变成(2,1),正好对应点B的位置,所以点 A向正南方向移动2 cm,再向正西方向移动2 cm,点A 到达点B 的位置。
故答案为:B。
将一条线段AB从中点O截断,使OA绕其端点O旋转180°,OA与OB重合;
在平面图上通常确定的方位是:上北下南、左西右东;
如果一个点在平面直角坐标系中向右移动, 其x坐标会增加; 向上移动, 其y坐标会增加。
16.C
解:1.2>1,所以甲×1.2>甲,乙÷1.2<乙,而甲×1.2=乙÷1.2,所以甲<乙。
故答案为:C。
一个非0数乘比1大的数,所得的结果比这个数大;一个非0数除以比1大的数,所得的结果比这个数小。据此作答即可。
17.D
解:A.6x+2>14,是含有未知数的不等式,不是方程,错误;
B.方程4.3x=0的解是x=0,错误;
C.等式两边同时乘或除以同一个不为0的数,左右两边仍然相等,错误;
D.2×(3+3)=12,所以x=3是方程2(x+3)=12的解,正确。
故答案为:D
根据方程的定义、等式的基本性质、方程的解,逐项判断即可。
18.A
解:图①的面积是:5×2÷2=5,
图②的面积是:4×2=8,
图③的面积是:3+3=6,
图④的面积是:(2+4)×4÷2=12,
图⑤的面积是:2×6=12;
图⑥的面积是:3×3=9,
图⑦的面积是:4×5-5×2÷2=20-5=15,
说法错误的是图②的面积等于图⑥的面积
故答案为:A。
三角形面积=底×高÷2,长方形面积=长×宽,平行四边形面积=底×高,梯形面积=(上底+下底)×高÷2。
19.
5-0.7=4.3 3.5a+0.5la=4.01a 3.87x-1.1x=2.77x 12.09+7.9=19.9
0.252=0.0625 5.6÷0.64=8.75 4.12÷0.2=20.6 1.8×6.55=11.79
小数乘小数,先按照整数乘法去乘,再看因数中一共有几位小数,就从积的右边起数出几位点上小数点;除数是小数的小数除法,先移动除数的小数点,使它变成整数;除数的小数点向右移动几位,被除数的小数点也向右移动几位(位数不够的,在被除数的末尾用“0”补足),然后按照除数是整数的小数除法进行计算;小数加、减法,先把小数点对齐再计算;含有字母的式子求值,可根据小数的运算律计算。
20.解:0.45×2.48=1.116
3.36÷9.6=0.35
9.68÷5.2≈1.86
小数乘法计算方法:先按整数乘法算出积,再点小数点;点小数点时,看因数中一共有几位小数,就从积的右边起数出几位,点上小数点;
一个数除以小数,先移动除数的小数点,使它变成整数;除数的小数点向右移动几位,被除数的小数点也向右移动几位;位数不够时,在被除数的末尾用0补足;最后按照除数是整数的除法进行计算;
求一个小数的近似数,先看要求保留到那一位,然后再向后多看一位,把多看的这一位数四舍五入。
21.
19-x=13
解:19-x+x=13+x
13+x=19
13+x-13=19-13
x=6
x÷=6÷
x=16 x-x=
解:x=
x÷=÷
x=2
x÷20%=×2.4
解:x÷20%=2.1
x÷20%×20%=2.1×20%
x=0.42
x+x=7.8
解:x=7.8
x÷=7.8÷
x=6.5
x÷=14
解:x÷×=14×
x=8
x÷=8÷
x= 50%x-33%x=34
解:17%x=34
17%x÷17%=34÷17%
x=200
75%x-x=15
解:0.25x=15
0.25x÷0.25=15÷0.25
x=60
x÷(1-40%)=3.6
解:x÷60%=3.6
x÷60%×60%=3.6×60%
x=2.16
5x-3×=
解:5x-=
5x-+=+
5x=
5x÷5=÷5
x=
等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等;等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
解含有百分数的方程,需要先将百分数化为分数或小数,再利用等式的性质来求解。
22.解:⑴9.6-5.98÷4.6×6.4
=9.6-1.3×6.4
=9.6-8.32
=1.28
⑵ 0.137×5.8+1.37×0.32+0.137
=0.137×5.8+0.137×10×0.32+0.137
=0.137×(5.8+10×0.32+1)
=0.137×10
=1.37
⑶1.08× (5.2+2.99÷2.3)
=1.08× (5.2+1.3)
=1.08×6.5
=7.02
⑷9.27÷0.125÷80
=9.27÷(0.125×80)
=9.27÷10
=0.927
(1)按顺序计算,首先计算除法和乘法,然后计算减法即可;
(2)首先将1.37写成0.137×10,然后根据乘法分配律得到0.137×(5.8+10×0.32+1),最后按顺序计算即可;
(3)按顺序计算,首先计算小括号内的除法和加法,然后计算乘法即可;
(4)首先根据乘法结合律,得到9.27÷(0.125×80),然后先计算小括号内的乘法,再计算除法即可。
23.(1)影长;竿高;1.5x;正
(2)
(3)解:影长1.5米,竿高 1米;竿高 7米,影长 10.5米。
解:(1)表中影长随着竿高的变化而变化,y=1.5x,即y÷x=1.5,所以成正比例;
故答案为:(1)影长;竿高;1.5x;正。
(1)观察表格可知,竿高随着影长的增加而增加,且影长是竿高的1.5倍,据此写出关系式,两个相关联的量,如果比值一定,那么成正比例,影长与竿高的比值为1.5(一定),所以成正比例;
(2)根据描点法,先依次找出各点,然后顺序把各点连起来即可;
(3)根据图示,竿高与影长的关系是一条直线,当影长是1.5米时,竿高是1米;当竿高是7米时,影长是10.5米。
24.(1)(3,5)
(2)西;北;45
(3)4.5
(4)
(5)
解:(1)点B在第3列,第5行,所以点B的位置是:(3,5);
(2)三角形ABC是一个等腰直角三角形,ACB=45°,根据图上的方向标可知,点A在点C的西偏北45°方向上;
(3)332=4.5( cm2 );
故答案为:(1)(3,5);(2)西;北;45;(3)4.5。
(1)数对表示位置时,前一个数字表示列,后一个数字表示行;
(2)西偏北45 ° 是从正西方向向正北方向偏移45 ° ;
(3)三角形的面积=底高2;
(4)逆时针旋转90°:先给三角形的三个顶点分别表上字母A、B、C,然后将线段AC和线段BC绕点C分别逆时针旋转90°,得到线段A′C和B′C,最后将点A′和B′连在一起;
(5) 将图形按2:1放大:将三角形的两条直角边放大至32=6格,然后将两条直角边的另一顶点相连,画出底为6格、高为6格的三角形。
25.(1)解:(6+15)×7÷2
=21×7÷2
=147÷2
=73.5(平方米)
答:梯形菜地的面积是73.5平方米。
(2)解:15×(9-7)÷2
=15×2÷2
=15(平方米)
答:三角形菜地的面积是15平方米。
(1)梯形面积=(上底+下底)×高÷2,根据公式计算梯形面积;
(2)三角形面积=底×高÷2,三角形底是15米,所在的高是(9-7)米,由此计算面积。
26.解:设今天2月有x万人参观了上海科技馆。
8x=195
8x÷8=195÷8
x=24.375
答:今天2月有24.375万人参观了上海科技馆。
设今天2月有x万人参观了上海科技馆。依据等量关系:8×今天2月参观上海科技馆的人数= 2022年2月参观上海科技馆的人数,列方程,解方程。
27.解:60÷(1.25×2)
=60÷2.5
=24(天)
答:这支牙膏够笑笑用24天。
这支牙膏够笑笑用的天数=这支牙膏的总质量÷平均每天用的质量;其中,平均每天用的质量=一天早晚两次用掉的质量和。
28.(1)解:9.8×1.8=17.64(元)
答: 小明家7月份应付水费17.64元
(2)解:第一段费用:10×1.8=18(元)
第二段费用:31.2-18=13.2(元)
用水量:13.2÷2.4=5.5(吨)
小明家8月份用水量:10+5.5=15.5(吨)
答:小明家8月份用水量15.5吨。
分段计费问题,
(1)根据单价乘以数量=总价直接计算。
(2)第一段费用18元,第二段费用24,两段总费用42元,故8月份用水量不超过20吨。用总价除以单价=用水量。
29.解:两车相遇时甲走了全程的 ,乙走了全程的;
相遇后甲乙两车的速度比:
甲到达B地时,乙走了全程的:
与A地的距离:
则A、B两地的距离:
(千米)
答:A、B两地相距450千米。
设A、B两地的距离这两个未知数为x千米,利用速度比和相遇后的速度变化来建立方程,解方程即可。
同课章节目录
