2024-2025学年浙教版八年级数学上册期末临考猜题卷 (含答案+解析)
文档属性
| 名称 | 2024-2025学年浙教版八年级数学上册期末临考猜题卷 (含答案+解析) |  | |
| 格式 | docx | ||
| 文件大小 | 408.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-12 10:50:16 | ||
图片预览




文档简介
保密★启用前
2024-2025学年八年级上册期末临考猜题卷(浙教版)
数学
考试范围:八上全册 考试时间:100分钟 分值:120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、单选题
1.在下列图形中, 是轴对称图形有 ( ) 个
A.1 B.2 C.3 D.4
2.下列算式的运算结果正确的是( )
A. B.
C. D.
3.如图,在△ABC中,AB=AC,AD=DE,∠BAD=20°,∠EDC=10°,则∠DAE的度数为( )
A.30° B.40° C.60° D.80°
4.下列命题的逆命题是真命题的是( )
A.对顶角相等 B.全等三角形的对应角相等
C.若,则 D.两直线平行,同位角相等
5.若关于一元二次方程有实数解,则的取值范围是( )
A. B.
C.且 D.且
6.已知x,y为实数,且,则下列式子的值最大的是( ).
A. B. C. D.
7.在平面直角坐标系中,若,,则一次函数的图象大致是( )
A. B.
C. D.
8.如图,在中,,,点是边的中点,射线,是射线上的一个动点,将点绕着点顺时针旋转90°得到点,则线段长度的最小值为( )
A. B.1.5 C.2 D.1
9.如图,在中,,,,动点从点出发,以每秒个单位的速度沿的路径运动,同时点从出发,以相同的速度沿的路径运动,当点运动到点时,,两点停止运动,过点作,过点作,设点运动的时间为,四边形与重叠的面积为,则与之间的函数关系用图象表示大致是( )
A. B. C. D.
10.如图,AB为半圆 O 的直径, 分别切 于 两点, 切 于点 , 连结 , 下列结论:
①,②,③,④,⑤, 正确的有( )
A.①②③④ B.②③④⑤ C.①②③⑤ D.①②③
二、填空题
11.已知 是关于 的反比例函数, 与 成正比例, 当 时, ; 当 时, .
写出 关于 的函数表达式: ;
当 时, 的值为: .
12.如图,点是矩形的对称中心,点,分别在边,上,且经过点,,,,点是边上一动点.则周长的最小值为 .
13.已知关于x的方程的两根分别为,,则的值为 .
14.如图,在中,已知平分,且于点D,的面积是8,则的面积是 .
15.若关于的不等式组有且只有2个偶数解,且关于的分式方程有正数解,则符合条件的所有整数的积为 .
16.如图,已知直线与轴交于点,点与点关于轴对称.是直线上的动点,将绕点顺时针旋转得.连接,则线段的最小值为 .
三、解答题
17.计算:
(1);
(2);
;
.
18.解下列方程:
(1)
(3)
19.计算:
(1)解不等式:.
(2)解不等式组,并将不等式组的解集在数轴上表示出来.
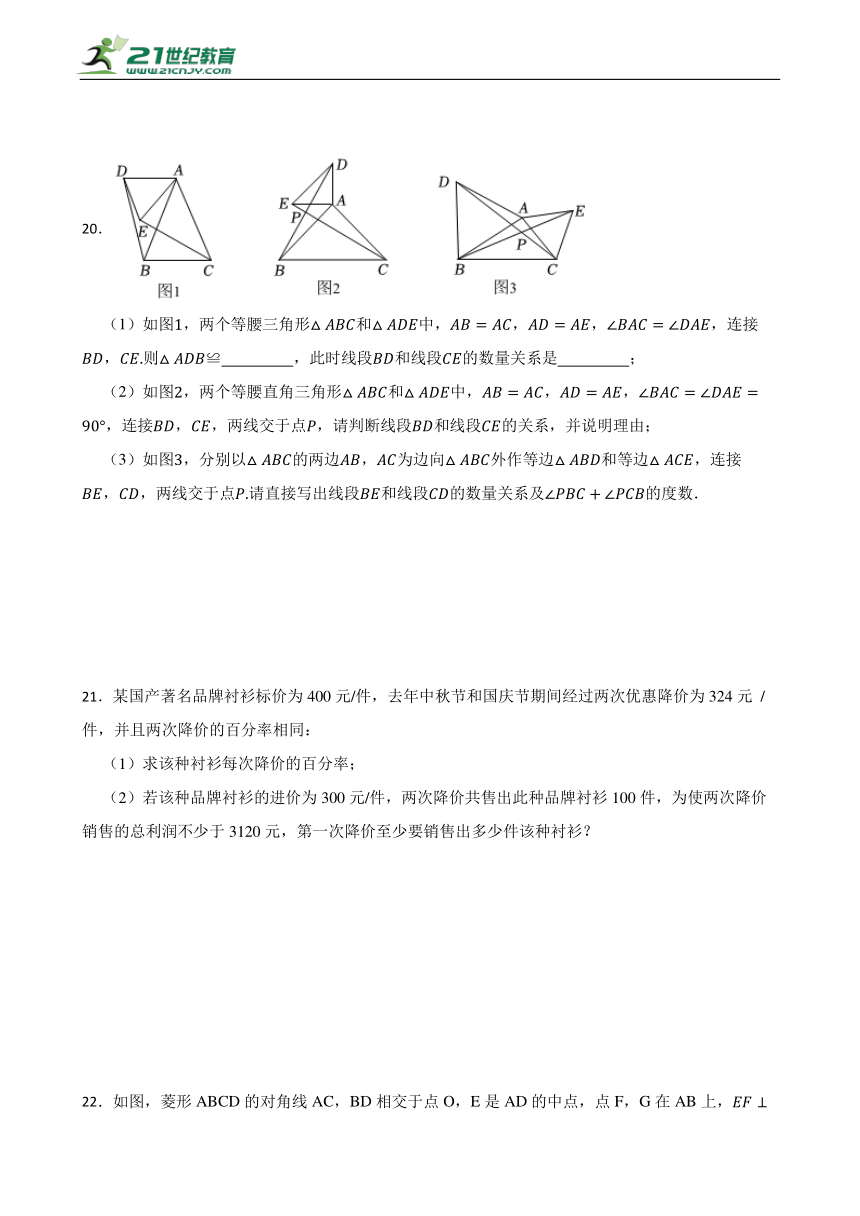
20.
(1)如图,两个等腰三角形和中,,,,连接,则≌ ,此时线段和线段的数量关系是 ;
(2)如图,两个等腰直角三角形和中,,,,连接,,两线交于点,请判断线段和线段的关系,并说明理由;
(3)如图,分别以的两边,为边向外作等边和等边,连接,,两线交于点请直接写出线段和线段的数量关系及的度数.
21.某国产著名品牌衬衫标价为400元/件,去年中秋节和国庆节期间经过两次优惠降价为324元 /件,并且两次降价的百分率相同:
(1)求该种衬衫每次降价的百分率;
(2)若该种品牌衬衫的进价为300元/件,两次降价共售出此种品牌衬衫100件,为使两次降价销售的总利润不少于3120元,第一次降价至少要销售出多少件该种衬衫?
22.如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,,.
(1)求证:四边形OEFG是矩形;
(2)若,,求BG的长.
23.如图,在四边形中,,,对角线、交于点O,平分,过点C作交的延长线于点E,连接.
(1)求证:四边形是菱形.
(2)若,,则的长为 .
24.如图,在平面直角坐标系中,点在轴的正半轴上,点的坐标为,线段轴.动点从点出发,沿方向运动;同时,动点从原点出发,沿轴向右运动,动点,的运动速度均为1个单位长度/秒.当点到达终点时,点也随之停止运动.连接,过的中点作垂直于的线段,点在右侧且,如图①.设运动时间为秒.
(1)当时,点的坐标为___________;点的坐标为___________;
(2)当点落在轴上时,求的值;
(3)如图②,连接,,探究的面积是否为定值?若是,请求出该定值;若不是,请说明理由.
25.如图①,已知直线与x轴、y轴分别交于点A、C,以OA、OC为边在第一象限内作长方形OABC.
(1)求点A、C的坐标;
(2)将△ABC对折,使得点A与点C重合,折痕交AB于点D,求直线CD的解析式(图②);
(3)在坐标平面内,是否存在点P(除点B外),使得△APC与△ABC全等,若存在,请求出所有符合条件的点P的坐标,若不存在,请说明理由.
答案解析部分
1.C
解:第一、第二、第四个图形都能找到这样的一条直线,使这些图形沿着一条直线对折后两部分完全重合,所以是轴对称图形,
第三个图形找到这样的一条直线,使这个图形沿着一条直线对折后两部分完全重合,所以不是轴对称图形,
所以是轴对称图形有3个.
故答案为:C.
利用轴对称图形的定义(如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴)逐项分析判断即可.
2.C
A、 ,此项不符合题意;
B、 , 此项不符合题意;
C、 ,此项符合题意;
D、 , 此项不符合题意;
故答案为:C.
根据二次根式的性质、二次根式的加减、积的乘方及合并同类项分别计算,再判断即可.
3.C
4.D
解:
A、逆命题是相等的角是对顶角,为假命题,A不符合题意;
B、逆命题是对应角相等的三角形是全等三角形,为假命题,B不符合题意;
C、逆命题是若,则,为假命题,C不符合题意;
D、逆命题是同位角相等,两直线平行,为真命题,D符合题意;
故答案为:D
根据逆命题定义写出各项逆命题,进而根据真命题和假命题对选项逐一判断即可求解。
5.D
6.A
解:∵,
∴,,
∴,,
∴,,,,
∴的值最大,
故答案为:A.
根据算术平方根及偶数次幂的非负性,由两个非负数的和为零,则每一个数都等于零可求出x、y的值,然后分别代入四个选项所给代数式计算后比较大小即可.
7.B
解:,
,
,
一次函数的图象经过一、二、三象限,
故答案为:B.
根据一次函数的性质“ 一次函数(为常数,)是一条直线,当时,图象经过一、三象限,随的增大而增大,当时,图象经过二、四象限,随的增大而减小,图象与轴的交点坐标为 ”解题即可.
8.A
解:连接AP′并延长,
∵是射线上的一个动点,将点绕着点顺时针旋转90°得到点 ,
∴CP′=CP,∠PCP′=90°,
在Rt△ACB中,AC=BC,
∴∠CAB=∠CBA=45°,
∴AB=BC=4,
∵BE∥AC,
∴∠CBP=∠ACB=90°,∠ACP′+∠BCP′=90°=∠BCP+∠BCP′,
∴∠ACP′=∠BCP,
在△CAP′和△CBP中
∴△CAP′≌△CBP(SAS)
∴∠CAP′=∠CBP=90°,
∴点P′运动轨迹过点A且垂直于直线AC的射线,即点P在射线AP′上运动,
当DP′⊥AP′时,线段DP′的长度最小,
∵点D是AB的中点,
∴在Rt△ADP′中,∠DAP′=90°-∠CAB=45°,∠AP′D=90°,
∴AP′=DP′
∵点D是AB的中点,
∴AD=AB=2,
∴线段DP′的最小值为DP′=
故答案为:A
连接AP′并延长,利用旋转的性质可证得CP′=CP,∠PCP′=90°,利用解直角三角形求出AB的长,利用平行线的性质及余角的性质去证明∠CBP=∠ACB=90°,∠ACP′=∠BCP,利用SAS证明△CAP′≌△CBP,由此可得到∠CAP′=90°,可推出点P′运动轨迹过点A且垂直于直线AC的射线,即点P在射线AP′上运动,利用垂线段最短,可知当DP′⊥AP′时,线段DP′的长度最小;然后求出AD的长,利用解直角三角形求出DP′的长即可.
9.D
10.C
解:连接OE,如图所示:
∵AD与圆O相切,DC与圆O相切,BC与圆O相切,
∴∠DAO=∠DEO=∠OBC=90°,
∴DA=DE,CE=CB,AD∥BC,
∴CD=DE+EC=AD+BC,选项②正确;
在Rt△ADO和Rt△EDO中,
∴Rt△ADO≌Rt△EDO(HL),
∴∠AOD=∠EOD,
同理Rt△CEO≌Rt△CBO,
∴∠EOC=∠BOC,
又∠AOD+∠DOE+∠EOC+∠COB=180°,
∴2(∠DOE+∠EOC)=180°,即∠DOC=90°,选项①正确;
∴∠DOC=∠DEO=90°,又∠EDO=∠ODC,
∴△EDO∽△ODC,
∴=,即OD2=DC DE,选项⑤正确;
∵∠AOD+∠COB=∠AOD+∠ADO=90°,∠A=∠B=90°,
∴△AOD∽△BOC,
∴=()2=()2=,选项③正确;
同理△ODE∽△OEC,
∴=,选项④错误;
故答案为:C.
本题考查切线的性质,切线长定理,相似三角形的判定与性质,全等三角形的判定与性质.
连接OE,由AD,DC,BC都为圆的切线,利用圆的切线的性质可推出:∠DAO=∠DEO=∠OBC=90°,再利用切线长定理可得:DE=DA,CE=CB,由CD=DE+EC,等量代换可得出CD=AD+BC,据此可判断说法②;由AD=ED,OD为公共边,利用直角三角形全等的判定定理HL可证明:直角三角形ADO与直角三角形EDO全等,利用全等三角形的性质可得:∠AOD=∠EOD,同理可证明∠EOC=∠BOC,根据这四个角之和为平角,可推出∠DOC为直角,据此可判断说法①;由∠DOC与∠DEO都为直角,再根据∠EDO=∠ODC,利用两对对应角相等的两三角形相似可得:△EDO∽△ODC,利用相似得三角形的性质可得:OD2=DE CD,据此可判断说法⑤;利用相似三角形的判定定理可证明△AOD∽△BOC,利用相似三角形的性质可得=()2=()2=,据此可判断说法③;利用相似三角形的判定定理可证明:△ODE∽△OEC,利用相似三角形的性质可得:=,据此可判断说法④.
11.;1
解:∵y1是x的反比例函数,y2与x+1成正比例,
∴设y1=,y2=k2(x+1),
∵y=y1+y2,
∴y=+k2(x+1),
∵x=1,y=-2;x=-1,y=4;
∴,
解得:k1=-4,k2=1,
∴.
当x=-2时,
y==1.
故答案为:;1.
根据题意可设y1=,y2=k2(x+1),由y=y1+y2可得y=+k2(x+1),把题中的两组x、y的值代入可得关于k1、k2的方程组,解方程组求出k1、k2的值即可得到y关于x的函数解析式;把x=-2代入(1)中求得的y与x之间的关系式计算即可求解.
12.
解:如图,作关于的对称点,连接,交于,连接,作于,于,连结AC,
∵关于的对称点,,
,
的最小值为,
周长的最小值为,
点是矩形的对称中心,经过点,
OA=OC,∠AOP=∠COQ,AD//BC,
∠PAO=∠QCO,
△APO≌△CQO(ASA),
∵,
,
,
,
,
,,
,
周长的最小值为.
作关于的对称点,连接,交于,连接,作于,于,连结AC,则的最小值为,证明出周长的最小值为,先利用ASA证明△APO≌△CQO,可求得CQ的长,再利用线段的和差求出BQ,然后利用勾股定理求出和,周长的最小值就是和的和.
13.6
解:∵方程的两根分别为,,
∴,,
则,
故答案为:6.
根据一元二次方程根与系数的关系可得,,再根据配方法将代数式进行配方,再整体代入即可求出答案.
14.
解:如图,延长交于,
∵平分,
∴,
在和中,,
∴,
∴,
∴,,
∴,
∴,
故答案为:.
延长交于,得到,即可得到,然后根据三角形的中线平分三角形的面积相等得到,,最后利用解题即可.
15.30
16.
17.(1)
(2)
(3)
(4)36
18.(1),;
(2),;
(3),.
19.(1)解:去分母,得1+2x<3x-6.
移项,得2x-3x<-1-6.
合并同类项,得-x<-7.
系数化为1,得x>7.
(2)解:,
解①式得x≤2;
解②式得x>-4.
即解集为-4<x≤2.
在数轴上表示如下:
(1)去分母、移项并合并同类项,最后系数化为1即可解出x;
(2)解出每个不等式后合并解集,并在数轴上表示. 注意标示时实心点与空心点所代表的含义.
20.(1);
(2)解:且;
理由如下:,
.
即.
在和中,
,
≌,
,,
,
,
即,
,
,
综上所述:且;
(3)解:如图所示,,,理由如下:
和是等边三角形,
,,,
,
,
在和中,
,
≌,
,,
,
.
解:(1)∵ ,
∴,
即
在和中
∴
∴,
故答案为:,.
(1)由已知条件推出再利用“SAS”证明,即可得出结论;
(2)同理推根据“SAS”证明,得:进而求出,即可得出结论;
(3)根据等边三角形的性质推出,再利用“SAS”证明得:进而求最后利用三角形外角的性质,即可得出结论.
21.(1)解:该种衬衫每次降价的百分率为x,由题意得:
解得:(不合题意,舍去)
所以该种衬衫每次降价的百分率为10%;
(2)解:设第一次降价要销售出y件该种衬衫,由题意得:
解得:
所以第一次降价至少要销售出20件该种衬衫.
(1)该种衬衫每次降价的百分率为x,根据题意列出方程,再求解即可;
(2)设第一次降价要销售出y件该种衬衫,根据题意列出不等式,再求解即可。
22.(1)证明:∵四边形ABCD为菱形
∴OB=OD
∵点E为AD中点
∴
∵
∴四边形OEFG为平行四边形
∵EF⊥AB
∴平行四边形OEFG为矩形.
(2)解:由(1)知:AC⊥BD
∵点E为AD的中点,AD=20,
∴OE=AE=AD=10
∵四边形OEFG是矩形
∴FG=OE=10
在Rt△AEF中,
∴BG=AB-AF-FG=20-6-10=4.
(1)由OB=OD,点E为AD中点先证明,再结合得出四边形OEFG为平行四边形,有因为EF⊥AB即可得出结论
(2)先根据菱形的性质和直角三角形斜边的中线等于斜边的一半得出:OE=AE=AD=10,再根据勾股定理:,求出AF=6即可.
(1)证明:∵四边形ABCD为菱形,
∴OB=OD,
∵点E为AD中点,
∴OE为△ABD的中位线,
∴,
∵,
∴四边形OEFG为平行四边形,
∵EF⊥AB,
∴∠EFG=90°,
∴平行四边形OEFG为矩形;
(2)解:∵四边形ABCD是菱形,
∴AB=AD=20,OB=OD,AC⊥BD,
∵点E为AD的中点,AD=20,
∴OE=AE=AD=10,
由(1)可知,四边形OEFG是矩形,
∴∠EFG=∠AFE=90°,OG=EF=8,FG=OE=10,
∴,
∴BG=AB-AF-FG=20-6-10=4.
23.(1)解:∵ ,
∴ ,
∵ 为 的平分线,
∴ ,
∴ ,
∴ ,
∵ ,
∴四边形 是平行四边形,
∵ ,
∴ 是菱形;
(2)解:∵四边形 是菱形, ∴ , ∵ ,即 是直角三角形, ∴ , ∵ , ∴ , 在 中, , , ∴ , ∴ . 故答案是:2.
(1)根据平行线的性质求出 , 再根据角平分线求出 , 最后利用菱形的判定方法证明即可;
(2)利用菱形的性质求出 , 再求出 , 最后利用勾股定理计算求解即可。
24.(1),
(2)解:如图③,连接,
由题意,t秒时,,则,
∵M为的中点,
∴,
∵,
∴,
∴,,即轴,
∴是等腰直角三角形,且,
∴,,
∵,
∴,
∴;
综上,当点落在轴上时,;
(3)解:过N作轴于D,交于C,连接,,则,,,
∵,,
∴是等腰直角三角形,,则,
∵,,
∴,
在和中,
∴,
∴,,
∴,
∵,,∴,
∴,又,
∴,
∴,
故的面积为定值10.
(1)解:由题意,当时,,,
∵点的坐标为,轴,
∴,,
∴,
∴,,则,
∵M为的中点,
∴,
∴,
∵,
∴,
故答案为:,;
(1)先求得点,,进而可求出点M、N的坐标即可;
(2)连接,先得到是等腰直角三角形,得可,,然后列方程求解即可;
(3) 过N作轴于D,交于C,连接,,得到,即可得到,,进而求出,,然后得到,根据坐标与图形性质和三角形的面积公式解题即可.
25.(1)解:当x=0时,y=4,∴C(0,4);
当y=0时,-2x+4=0,解得,
∴A(2,0);
∴A(2,0);C(0,4).
(2)解:由折叠知:.
设则,
根据题意得:解得:
此时,,D(2,)
设直线CD为,把代入得 解得:
∴设直线CD解析式为;
(3)解:①当点P与点O重合时,,此时P(0,0)
②当点P在第一象限时,如图,
由得,
则点P在直线CD上.过P作于点Q,
在Rt△ADP中,
由得:
∴
∴,把代入得
此时P(,)
③当点P在第二象限时,如图,
由(2)同理可求得:
∴在Rt△PQC中,根据勾股定理
∴
此时
综合得,满足条件的点P有三个,分别为:(0,0);();(-).
(1)根据x、y轴上点的特点求得A和C的坐标;
(2)由折叠可得,再根据勾股定理可求出AD长,然后得到D点坐标,最后利用待定系数法求出CD的解析式;
(3)分为 点P与点O重合 ,点P在第一象限,点P在第二象限三种情况,根据全等三角形的判定和勾股定理得到点P的坐标即可.
2024-2025学年八年级上册期末临考猜题卷(浙教版)
数学
考试范围:八上全册 考试时间:100分钟 分值:120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、单选题
1.在下列图形中, 是轴对称图形有 ( ) 个
A.1 B.2 C.3 D.4
2.下列算式的运算结果正确的是( )
A. B.
C. D.
3.如图,在△ABC中,AB=AC,AD=DE,∠BAD=20°,∠EDC=10°,则∠DAE的度数为( )
A.30° B.40° C.60° D.80°
4.下列命题的逆命题是真命题的是( )
A.对顶角相等 B.全等三角形的对应角相等
C.若,则 D.两直线平行,同位角相等
5.若关于一元二次方程有实数解,则的取值范围是( )
A. B.
C.且 D.且
6.已知x,y为实数,且,则下列式子的值最大的是( ).
A. B. C. D.
7.在平面直角坐标系中,若,,则一次函数的图象大致是( )
A. B.
C. D.
8.如图,在中,,,点是边的中点,射线,是射线上的一个动点,将点绕着点顺时针旋转90°得到点,则线段长度的最小值为( )
A. B.1.5 C.2 D.1
9.如图,在中,,,,动点从点出发,以每秒个单位的速度沿的路径运动,同时点从出发,以相同的速度沿的路径运动,当点运动到点时,,两点停止运动,过点作,过点作,设点运动的时间为,四边形与重叠的面积为,则与之间的函数关系用图象表示大致是( )
A. B. C. D.
10.如图,AB为半圆 O 的直径, 分别切 于 两点, 切 于点 , 连结 , 下列结论:
①,②,③,④,⑤, 正确的有( )
A.①②③④ B.②③④⑤ C.①②③⑤ D.①②③
二、填空题
11.已知 是关于 的反比例函数, 与 成正比例, 当 时, ; 当 时, .
写出 关于 的函数表达式: ;
当 时, 的值为: .
12.如图,点是矩形的对称中心,点,分别在边,上,且经过点,,,,点是边上一动点.则周长的最小值为 .
13.已知关于x的方程的两根分别为,,则的值为 .
14.如图,在中,已知平分,且于点D,的面积是8,则的面积是 .
15.若关于的不等式组有且只有2个偶数解,且关于的分式方程有正数解,则符合条件的所有整数的积为 .
16.如图,已知直线与轴交于点,点与点关于轴对称.是直线上的动点,将绕点顺时针旋转得.连接,则线段的最小值为 .
三、解答题
17.计算:
(1);
(2);
;
.
18.解下列方程:
(1)
(3)
19.计算:
(1)解不等式:.
(2)解不等式组,并将不等式组的解集在数轴上表示出来.
20.
(1)如图,两个等腰三角形和中,,,,连接,则≌ ,此时线段和线段的数量关系是 ;
(2)如图,两个等腰直角三角形和中,,,,连接,,两线交于点,请判断线段和线段的关系,并说明理由;
(3)如图,分别以的两边,为边向外作等边和等边,连接,,两线交于点请直接写出线段和线段的数量关系及的度数.
21.某国产著名品牌衬衫标价为400元/件,去年中秋节和国庆节期间经过两次优惠降价为324元 /件,并且两次降价的百分率相同:
(1)求该种衬衫每次降价的百分率;
(2)若该种品牌衬衫的进价为300元/件,两次降价共售出此种品牌衬衫100件,为使两次降价销售的总利润不少于3120元,第一次降价至少要销售出多少件该种衬衫?
22.如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,,.
(1)求证:四边形OEFG是矩形;
(2)若,,求BG的长.
23.如图,在四边形中,,,对角线、交于点O,平分,过点C作交的延长线于点E,连接.
(1)求证:四边形是菱形.
(2)若,,则的长为 .
24.如图,在平面直角坐标系中,点在轴的正半轴上,点的坐标为,线段轴.动点从点出发,沿方向运动;同时,动点从原点出发,沿轴向右运动,动点,的运动速度均为1个单位长度/秒.当点到达终点时,点也随之停止运动.连接,过的中点作垂直于的线段,点在右侧且,如图①.设运动时间为秒.
(1)当时,点的坐标为___________;点的坐标为___________;
(2)当点落在轴上时,求的值;
(3)如图②,连接,,探究的面积是否为定值?若是,请求出该定值;若不是,请说明理由.
25.如图①,已知直线与x轴、y轴分别交于点A、C,以OA、OC为边在第一象限内作长方形OABC.
(1)求点A、C的坐标;
(2)将△ABC对折,使得点A与点C重合,折痕交AB于点D,求直线CD的解析式(图②);
(3)在坐标平面内,是否存在点P(除点B外),使得△APC与△ABC全等,若存在,请求出所有符合条件的点P的坐标,若不存在,请说明理由.
答案解析部分
1.C
解:第一、第二、第四个图形都能找到这样的一条直线,使这些图形沿着一条直线对折后两部分完全重合,所以是轴对称图形,
第三个图形找到这样的一条直线,使这个图形沿着一条直线对折后两部分完全重合,所以不是轴对称图形,
所以是轴对称图形有3个.
故答案为:C.
利用轴对称图形的定义(如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴)逐项分析判断即可.
2.C
A、 ,此项不符合题意;
B、 , 此项不符合题意;
C、 ,此项符合题意;
D、 , 此项不符合题意;
故答案为:C.
根据二次根式的性质、二次根式的加减、积的乘方及合并同类项分别计算,再判断即可.
3.C
4.D
解:
A、逆命题是相等的角是对顶角,为假命题,A不符合题意;
B、逆命题是对应角相等的三角形是全等三角形,为假命题,B不符合题意;
C、逆命题是若,则,为假命题,C不符合题意;
D、逆命题是同位角相等,两直线平行,为真命题,D符合题意;
故答案为:D
根据逆命题定义写出各项逆命题,进而根据真命题和假命题对选项逐一判断即可求解。
5.D
6.A
解:∵,
∴,,
∴,,
∴,,,,
∴的值最大,
故答案为:A.
根据算术平方根及偶数次幂的非负性,由两个非负数的和为零,则每一个数都等于零可求出x、y的值,然后分别代入四个选项所给代数式计算后比较大小即可.
7.B
解:,
,
,
一次函数的图象经过一、二、三象限,
故答案为:B.
根据一次函数的性质“ 一次函数(为常数,)是一条直线,当时,图象经过一、三象限,随的增大而增大,当时,图象经过二、四象限,随的增大而减小,图象与轴的交点坐标为 ”解题即可.
8.A
解:连接AP′并延长,
∵是射线上的一个动点,将点绕着点顺时针旋转90°得到点 ,
∴CP′=CP,∠PCP′=90°,
在Rt△ACB中,AC=BC,
∴∠CAB=∠CBA=45°,
∴AB=BC=4,
∵BE∥AC,
∴∠CBP=∠ACB=90°,∠ACP′+∠BCP′=90°=∠BCP+∠BCP′,
∴∠ACP′=∠BCP,
在△CAP′和△CBP中
∴△CAP′≌△CBP(SAS)
∴∠CAP′=∠CBP=90°,
∴点P′运动轨迹过点A且垂直于直线AC的射线,即点P在射线AP′上运动,
当DP′⊥AP′时,线段DP′的长度最小,
∵点D是AB的中点,
∴在Rt△ADP′中,∠DAP′=90°-∠CAB=45°,∠AP′D=90°,
∴AP′=DP′
∵点D是AB的中点,
∴AD=AB=2,
∴线段DP′的最小值为DP′=
故答案为:A
连接AP′并延长,利用旋转的性质可证得CP′=CP,∠PCP′=90°,利用解直角三角形求出AB的长,利用平行线的性质及余角的性质去证明∠CBP=∠ACB=90°,∠ACP′=∠BCP,利用SAS证明△CAP′≌△CBP,由此可得到∠CAP′=90°,可推出点P′运动轨迹过点A且垂直于直线AC的射线,即点P在射线AP′上运动,利用垂线段最短,可知当DP′⊥AP′时,线段DP′的长度最小;然后求出AD的长,利用解直角三角形求出DP′的长即可.
9.D
10.C
解:连接OE,如图所示:
∵AD与圆O相切,DC与圆O相切,BC与圆O相切,
∴∠DAO=∠DEO=∠OBC=90°,
∴DA=DE,CE=CB,AD∥BC,
∴CD=DE+EC=AD+BC,选项②正确;
在Rt△ADO和Rt△EDO中,
∴Rt△ADO≌Rt△EDO(HL),
∴∠AOD=∠EOD,
同理Rt△CEO≌Rt△CBO,
∴∠EOC=∠BOC,
又∠AOD+∠DOE+∠EOC+∠COB=180°,
∴2(∠DOE+∠EOC)=180°,即∠DOC=90°,选项①正确;
∴∠DOC=∠DEO=90°,又∠EDO=∠ODC,
∴△EDO∽△ODC,
∴=,即OD2=DC DE,选项⑤正确;
∵∠AOD+∠COB=∠AOD+∠ADO=90°,∠A=∠B=90°,
∴△AOD∽△BOC,
∴=()2=()2=,选项③正确;
同理△ODE∽△OEC,
∴=,选项④错误;
故答案为:C.
本题考查切线的性质,切线长定理,相似三角形的判定与性质,全等三角形的判定与性质.
连接OE,由AD,DC,BC都为圆的切线,利用圆的切线的性质可推出:∠DAO=∠DEO=∠OBC=90°,再利用切线长定理可得:DE=DA,CE=CB,由CD=DE+EC,等量代换可得出CD=AD+BC,据此可判断说法②;由AD=ED,OD为公共边,利用直角三角形全等的判定定理HL可证明:直角三角形ADO与直角三角形EDO全等,利用全等三角形的性质可得:∠AOD=∠EOD,同理可证明∠EOC=∠BOC,根据这四个角之和为平角,可推出∠DOC为直角,据此可判断说法①;由∠DOC与∠DEO都为直角,再根据∠EDO=∠ODC,利用两对对应角相等的两三角形相似可得:△EDO∽△ODC,利用相似得三角形的性质可得:OD2=DE CD,据此可判断说法⑤;利用相似三角形的判定定理可证明△AOD∽△BOC,利用相似三角形的性质可得=()2=()2=,据此可判断说法③;利用相似三角形的判定定理可证明:△ODE∽△OEC,利用相似三角形的性质可得:=,据此可判断说法④.
11.;1
解:∵y1是x的反比例函数,y2与x+1成正比例,
∴设y1=,y2=k2(x+1),
∵y=y1+y2,
∴y=+k2(x+1),
∵x=1,y=-2;x=-1,y=4;
∴,
解得:k1=-4,k2=1,
∴.
当x=-2时,
y==1.
故答案为:;1.
根据题意可设y1=,y2=k2(x+1),由y=y1+y2可得y=+k2(x+1),把题中的两组x、y的值代入可得关于k1、k2的方程组,解方程组求出k1、k2的值即可得到y关于x的函数解析式;把x=-2代入(1)中求得的y与x之间的关系式计算即可求解.
12.
解:如图,作关于的对称点,连接,交于,连接,作于,于,连结AC,
∵关于的对称点,,
,
的最小值为,
周长的最小值为,
点是矩形的对称中心,经过点,
OA=OC,∠AOP=∠COQ,AD//BC,
∠PAO=∠QCO,
△APO≌△CQO(ASA),
∵,
,
,
,
,
,,
,
周长的最小值为.
作关于的对称点,连接,交于,连接,作于,于,连结AC,则的最小值为,证明出周长的最小值为,先利用ASA证明△APO≌△CQO,可求得CQ的长,再利用线段的和差求出BQ,然后利用勾股定理求出和,周长的最小值就是和的和.
13.6
解:∵方程的两根分别为,,
∴,,
则,
故答案为:6.
根据一元二次方程根与系数的关系可得,,再根据配方法将代数式进行配方,再整体代入即可求出答案.
14.
解:如图,延长交于,
∵平分,
∴,
在和中,,
∴,
∴,
∴,,
∴,
∴,
故答案为:.
延长交于,得到,即可得到,然后根据三角形的中线平分三角形的面积相等得到,,最后利用解题即可.
15.30
16.
17.(1)
(2)
(3)
(4)36
18.(1),;
(2),;
(3),.
19.(1)解:去分母,得1+2x<3x-6.
移项,得2x-3x<-1-6.
合并同类项,得-x<-7.
系数化为1,得x>7.
(2)解:,
解①式得x≤2;
解②式得x>-4.
即解集为-4<x≤2.
在数轴上表示如下:
(1)去分母、移项并合并同类项,最后系数化为1即可解出x;
(2)解出每个不等式后合并解集,并在数轴上表示. 注意标示时实心点与空心点所代表的含义.
20.(1);
(2)解:且;
理由如下:,
.
即.
在和中,
,
≌,
,,
,
,
即,
,
,
综上所述:且;
(3)解:如图所示,,,理由如下:
和是等边三角形,
,,,
,
,
在和中,
,
≌,
,,
,
.
解:(1)∵ ,
∴,
即
在和中
∴
∴,
故答案为:,.
(1)由已知条件推出再利用“SAS”证明,即可得出结论;
(2)同理推根据“SAS”证明,得:进而求出,即可得出结论;
(3)根据等边三角形的性质推出,再利用“SAS”证明得:进而求最后利用三角形外角的性质,即可得出结论.
21.(1)解:该种衬衫每次降价的百分率为x,由题意得:
解得:(不合题意,舍去)
所以该种衬衫每次降价的百分率为10%;
(2)解:设第一次降价要销售出y件该种衬衫,由题意得:
解得:
所以第一次降价至少要销售出20件该种衬衫.
(1)该种衬衫每次降价的百分率为x,根据题意列出方程,再求解即可;
(2)设第一次降价要销售出y件该种衬衫,根据题意列出不等式,再求解即可。
22.(1)证明:∵四边形ABCD为菱形
∴OB=OD
∵点E为AD中点
∴
∵
∴四边形OEFG为平行四边形
∵EF⊥AB
∴平行四边形OEFG为矩形.
(2)解:由(1)知:AC⊥BD
∵点E为AD的中点,AD=20,
∴OE=AE=AD=10
∵四边形OEFG是矩形
∴FG=OE=10
在Rt△AEF中,
∴BG=AB-AF-FG=20-6-10=4.
(1)由OB=OD,点E为AD中点先证明,再结合得出四边形OEFG为平行四边形,有因为EF⊥AB即可得出结论
(2)先根据菱形的性质和直角三角形斜边的中线等于斜边的一半得出:OE=AE=AD=10,再根据勾股定理:,求出AF=6即可.
(1)证明:∵四边形ABCD为菱形,
∴OB=OD,
∵点E为AD中点,
∴OE为△ABD的中位线,
∴,
∵,
∴四边形OEFG为平行四边形,
∵EF⊥AB,
∴∠EFG=90°,
∴平行四边形OEFG为矩形;
(2)解:∵四边形ABCD是菱形,
∴AB=AD=20,OB=OD,AC⊥BD,
∵点E为AD的中点,AD=20,
∴OE=AE=AD=10,
由(1)可知,四边形OEFG是矩形,
∴∠EFG=∠AFE=90°,OG=EF=8,FG=OE=10,
∴,
∴BG=AB-AF-FG=20-6-10=4.
23.(1)解:∵ ,
∴ ,
∵ 为 的平分线,
∴ ,
∴ ,
∴ ,
∵ ,
∴四边形 是平行四边形,
∵ ,
∴ 是菱形;
(2)解:∵四边形 是菱形, ∴ , ∵ ,即 是直角三角形, ∴ , ∵ , ∴ , 在 中, , , ∴ , ∴ . 故答案是:2.
(1)根据平行线的性质求出 , 再根据角平分线求出 , 最后利用菱形的判定方法证明即可;
(2)利用菱形的性质求出 , 再求出 , 最后利用勾股定理计算求解即可。
24.(1),
(2)解:如图③,连接,
由题意,t秒时,,则,
∵M为的中点,
∴,
∵,
∴,
∴,,即轴,
∴是等腰直角三角形,且,
∴,,
∵,
∴,
∴;
综上,当点落在轴上时,;
(3)解:过N作轴于D,交于C,连接,,则,,,
∵,,
∴是等腰直角三角形,,则,
∵,,
∴,
在和中,
∴,
∴,,
∴,
∵,,∴,
∴,又,
∴,
∴,
故的面积为定值10.
(1)解:由题意,当时,,,
∵点的坐标为,轴,
∴,,
∴,
∴,,则,
∵M为的中点,
∴,
∴,
∵,
∴,
故答案为:,;
(1)先求得点,,进而可求出点M、N的坐标即可;
(2)连接,先得到是等腰直角三角形,得可,,然后列方程求解即可;
(3) 过N作轴于D,交于C,连接,,得到,即可得到,,进而求出,,然后得到,根据坐标与图形性质和三角形的面积公式解题即可.
25.(1)解:当x=0时,y=4,∴C(0,4);
当y=0时,-2x+4=0,解得,
∴A(2,0);
∴A(2,0);C(0,4).
(2)解:由折叠知:.
设则,
根据题意得:解得:
此时,,D(2,)
设直线CD为,把代入得 解得:
∴设直线CD解析式为;
(3)解:①当点P与点O重合时,,此时P(0,0)
②当点P在第一象限时,如图,
由得,
则点P在直线CD上.过P作于点Q,
在Rt△ADP中,
由得:
∴
∴,把代入得
此时P(,)
③当点P在第二象限时,如图,
由(2)同理可求得:
∴在Rt△PQC中,根据勾股定理
∴
此时
综合得,满足条件的点P有三个,分别为:(0,0);();(-).
(1)根据x、y轴上点的特点求得A和C的坐标;
(2)由折叠可得,再根据勾股定理可求出AD长,然后得到D点坐标,最后利用待定系数法求出CD的解析式;
(3)分为 点P与点O重合 ,点P在第一象限,点P在第二象限三种情况,根据全等三角形的判定和勾股定理得到点P的坐标即可.
同课章节目录
