2024-2025学年苏科教版七年级数学上册期末临考猜题卷 (含答案+解析)
文档属性
| 名称 | 2024-2025学年苏科教版七年级数学上册期末临考猜题卷 (含答案+解析) |  | |
| 格式 | docx | ||
| 文件大小 | 655.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-12 10:54:40 | ||
图片预览




文档简介
保密★启用前
2024-2025学年七年级上册期末临考猜题卷(苏科教版)
数学
考试范围:七上全册 考试时间:100分钟 分值:120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、单选题(每题2分,共16分)
1.下列各组数中,互为相反数的是( )
A.﹣2与|﹣2| B.﹣2与﹣|﹣2|
C.﹣2与﹣ D.2与|﹣2|
2.若实数在数轴上的位置如图所示,则化简的结果为( )
A. B. C. D.
3.定西市图书馆的建筑面积为16191平方米,阅览席有2000余个,馆藏各类文献资料共41.5万余册,数据41.5万用科学记数法表示应为( )
A. B. C. D.
4.如图,下列关于数m、n的说法正确的是( )
A.m>n B.m=n C.m>﹣n D.m=﹣n
5.如图,C 是线段AB 上一点,M是AC 的中点,N 是 BC 的中点,如果 MC 比 NC 长4 cm,那么 AC 比 BC长( )
A.8cm B.6 cm C.4 cm D.2cm
6.如图,∠AOC为直角,OC是∠BOD的平分线,且∠AOB=57.65°,则∠AOD的度数是( )
A.122°20' B.122°21' C.122°22' D.122°23'
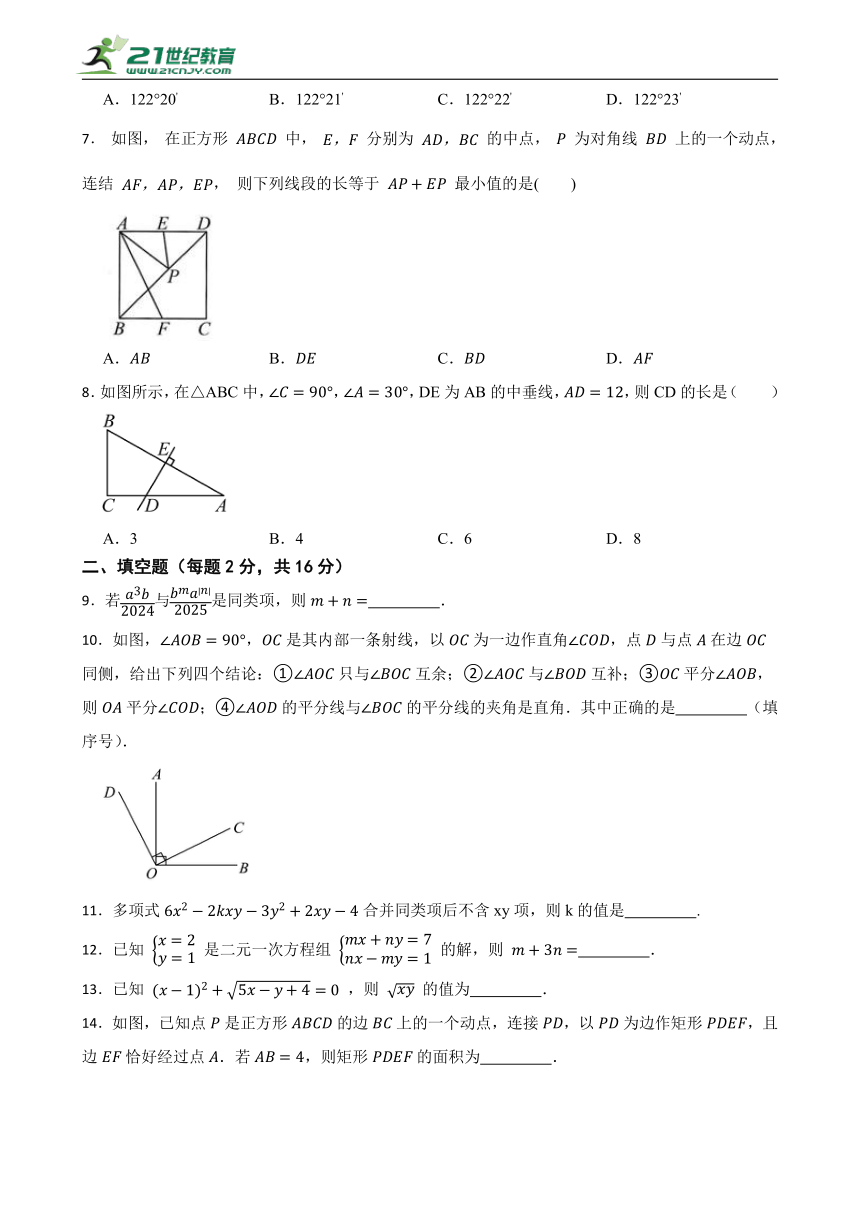
7. 如图, 在正方形 中, 分别为 的中点, 为对角线 上的一个动点, 连结 , 则下列线段的长等于 最小值的是( )
A. B. C. D.
8.如图所示,在△ABC中,,,DE为AB的中垂线,,则CD的长是( )
A.3 B.4 C.6 D.8
二、填空题(每题2分,共16分)
9.若与是同类项,则 .
10.如图,,是其内部一条射线,以为一边作直角,点与点在边同侧,给出下列四个结论:①只与互余;②与互补;③平分,则平分;④的平分线与的平分线的夹角是直角.其中正确的是 (填序号).
11.多项式合并同类项后不含xy项,则k的值是 .
12.已知 是二元一次方程组 的解,则 .
13.已知 ,则 的值为 .
14.如图,已知点是正方形的边上的一个动点,连接,以为边作矩形,且边恰好经过点.若,则矩形的面积为 .
15.如图, 在 中, 是 的垂直平分线, 且分别交 于点 和 , , 则 .
16.设表示不超过x的最大整数{例如:请你认真理解的意义,当,若,则的值为 .
三、解答题(共10题,共68分)
17. 如图是由6个棱长都为1的小正方体搭成的几何体.
左视图 俯视图
(1)请在下面方格纸中分别画出它的左视图和俯视图;
(2)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的左视图和俯视图不变,那么最多可以添加 个小正方体.
先化简,再求值:,其中,.
19.计算
(1)
20.解下列方程:
(1)2(x-2)-3(4x-1)=5(1-x).
21.在正方形网格中,每个小正方形的边长都为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC向右平移3格,再向下平移2格,得到△DEF,使点A的对应点为点D,点B的对应点为点E,点C的对应点为点F.
(1)画出△DEF;
(2)在图中画出△ABC的AB边上的高线CG(保留利用格点的作图痕迹);
(3)△ABC的面积为 ;
(4)若AB的长为5,AB边上的高 .
22. 已知二元一次方程.
(1)写出此方程的所有正整数解.
(2)若二元一次方程组存在x,y互为相反数的解,请在横线处补上一个方程,并求出此方程组的解.
23.(1)如图,C为线段上一点,点B为的中点,且,求的长.
(2)如图,已知∠平分,若,求的度数.
24.如图,已知四点A,B,C,D,请用直尺按要求完成作图,
(1)作射线AD;
(2)作直线BC;
(3)连接BD,请在BD上确定点P,使的值最小,依据是 .
25.如图,在平面直为坐标系中,点A,B的坐标分别为,,且a、b满足,现同时将点A,B分别向下平移2个单位,再向左平移1个单位,分别得到点A,B的对应点C,D,连接,,.
(1)求点C,D的坐标及四边形的面积;
(2)在y轴上是否存在一点M,连接,,使?若存在这样一点,求出点M的坐标,若不存在,试说明理由;
(3)点P是直线上的一个动点,连接,,当点P在直线上移动时(不与B,D重合),直接写出,,之间满足的数量关系.
26. 如图 1,点O为直线MN上一点,将一副三角板摆放在直线MN同侧,将60°角的顶点与45°角的顶点重合放在点O处,三角板OAB的顶点A与三角板OCD的顶点D在直线MN上,三角板OCD保持不动,三角板OAB绕点O以每秒10°的速度顺时针旋转一周,设旋转时间为t s.
(1)如图2,当OB平分∠AOC时,求t的值;
(2)当∠AOC=∠BOD时,画出相应的图形,并求t的值;
(3)三角板OAB在旋转过程中,若OP平分∠AOC,OQ平分∠BOC,直接写出∠POQ的度数.
答案解析部分
1.A
解:A、﹣2与|﹣2|=2,互为相反数,故此选项符合题意;
B、﹣2与﹣|﹣2|=﹣2,两数相等,故此选项不符合题意;
C、﹣2与﹣ ,两数相加不为零,故此选项不符合题意;
D、2与|﹣2|=2,两数相等,故此选项不符合题意;
故答案为:A.
直接利用相反数的定义以及绝对值的性质化简进而得出答案.
2.C
3.C
解:41.5万.
故选:C.
本题主要考查科学记数法,根据科学记数法的表示方法求解即可.科学记数法的表示形式为的形式,其中a为整数,确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同,据此即可作答.
4.D
∵m和n在原点两侧,且到原点的距离相等,
∴m和n是互为相反数,即m=-n;
故答案为:D。
根据数轴上所表示的数的特点:原点右边表示正数,原点左边表示负数,右边的数总比左边的数大,互为相反数的两个数位于原点的两侧,到原点的距离相等,从而即可一一判断得出答案。
5.A
解:∵ M是AC 的中点,
∴AC=2MC=2AM,
∵N 是 BC 的中点,
∴BC=2CN=2BN.
∵MC-NC=4cm,
∴AC-BC=2MC-2CN=2(MC-NC)=8cm.
故答案为:A.
根据线段中点的定义可得AC=2MC=2AM,BC=2CN=2BN.最后代入AC-BC,即可得到答案.
6.B
7.D
解:连接CE,AP,如图,
点A,C关于BD对称,则AP+EP的最小值为EC,
设正方形的边长为2a,则DE=a,
∴ EC=,
∵ AB=2a,DE=a,BD=a,AF=a,
∴ AP+EP的最小值是AF的长.
故答案为:D.
根据正方形的性质和轴对称,可得AP+EP的最小值为EC,根据勾股定理可得EC和AF的长,即可求得.
8.C
9.4或
10.②③④
11.1
解:由题意可得:
=
∵不含xy项
∴2k-2=0
解得:k=1
故答案为:1
合并同类项,根据不含xy项,可得其系数为0,列出方程,解方程即可求出答案.
12.8
解:由题意得 ,
①+②得,m+3n=8.
13.3
解:由题意得:,
解得,
∴==3.
故答案为:3.
两个非负数之和等于0,则每个非负数等于0,依此列方程组求解,再代值计算即可.
14.
15.70°
解:∵∠B=60°,∠C=25°,
∴∠BAC=180°-∠B-∠C=95°.
∵DE是AC的垂直平分线,
∴AD=CD,
∴∠DAC=∠C=25°,
∴∠BAD=∠BAC-∠DAC=70°
故答案为:70°.
利用三角形内角和定理求得∠BAC,再利用线段垂直平分线的性质得DA=DC,继而可得∠DAC的度数,利用角的和差运算即可得到结论.
16.4
解: ,
,
又 表示不超过x的最大整数 ,
, ,,,等于0,或等于1,
,
, ,,,中应共有32个1,47个0,
= == =0, = ===1,
,,
解得:,
=4.
故答案为:4.
根据, 表示不超过x的最大整数 ,得到 , ,,,等于0,或等于1,再根据,可得到 , ,,,中应共有32个1,47个0,进而得到,,解得a的取值范围,即可求解.
17.(1)解:如图所示:
左视图 俯视图
(2)2
解:(1)如图所示:
(2)保持这个几何体的左视图和俯视图不变,那么最多可以添加2个,
故答案为:2.
(1)根据三视图的概念作图即可得出答案;
(2)保持这个几何体的左视图和俯视图不变,那么最多可以在后面一行第一列和第二列各添加一个小正方体即可。
18.解:
,
当,时,原式
先运用完全平方公式,平方差公式运算,并合并同类项,然后运用多项式除以单项式的法则解题,最后代入x,y即可解题.
19.(1)
(2)
(3)
(4)
20.(1)解:去括号得,2x-4-12x+3=5-5x,
移项得,2x-12x+5x=5+4-3,
合并同类项得,-5x=6,
系数化为1得,;
(2)解:去分母得,2(2x-1)-(x+5)=6(2x+1),
去括号得,4x-2-x-5=12x+6,
移项得,4x-x-12x=6+2+5,
合并同类项得,-9x=13,
系数化为1得,.
(1)先去括号,再移项,合并同类项,最后系数化为1,即可解方程;
(2)先去分母,再去括号,移项,最后合并同类项和系数化为1,即可解方程.
21.(1)解:如图,将△ABC的三个顶点分别向右平移3格,再向下平移2格,得到对应点的位置,顺次连接即可得到△DEF;
(2)解:如图,利用格点的特点,过C点作AB的垂线CN,交AB于点G,CG即为AB边上的高线;
(3)
(4)
解:(3)△ABC的面积为:,
故答案为:;
(4)由(3)得,
∴,
∵,
∴,
解得.
故答案为:.
(1)利用方格纸的特点,分别将点A、B、C向右平移3格,再向下平移2格可得点D、E、F的位置,然后顺次连接即可;
(2)过C点作AB的垂线CN,交AB于点G,CG即为AB边上的高线;
(3)利用方格纸的特点及割补法,用△ABC外接正方形的面积分别减去周围三个三角形的面积,即可求出△ABC的面积;
(4)直接根据三角形的面积公式结合(3)的结果可得CG的值.
22.(1)解:方程的正整数为:;
(2)解:方程组的解是互为相反数,
,
把代入得:
,
解得:,
,
,
括号处补的方程为:,
方程组为:,
①②得:,
把代入②得:,
方程组的解为:.
解:(1)∵2x+5y=24,
∴,
∵x、y都是正整数,
∴24-2x一定是5的倍数,
∴24-2x=20或24-2x=10,
∴x=2或x=7,
当x=2时,y=4;
当x=7时,y=2,
∴方程2x+5y=24的正整数解为;
(1)将2x+5y=24变形为用含x的式子表示y的形式,结合x、y都是正整数可得4-2x=20或24-2x=10,从而求解可求出x的值,进而代入即可求出y,即可得到方程的正整数解;
(2)根据方程组的解是互为相反数得到x=-y,将其代入2x+5y=24求出x,y的值,根据方程组解得定义即可得到括号处补的方程可为2x+3y=8;进而利用加减消元法解方程组,用①-②消去x求出y的值,再将y的值代入②可求出x的值,从而即可得到方程组的解.
23.解:(1)∵点B为的中点,,
又,
;
(2)设,则,
,
平分,
,
即,
,
.
(1)由点B为的中点,求得,结合和,即可求得的长,得到答案;
(2)设,得到,且,根据平分,得到,列出方程,求得方程的解,即可得到答案.
24.(1)解:射线AD是以点A为端点,延伸方向为AD方向,作射线如图所示
(2)解:直线BC向两方无限延伸,过点B,C作直线BC如图所示;
(3)两点之间,线段最短
(3)解:连接,交于点,这时最小,
理由:两点之间线段最短.
故答案为两点之间,线段最短.
(1)根据题意作射线AD即可;
(2)根据作直线的方法作图即可;
(3)根据两点之间线段最短求解即可。
25.(1)解:∵ ,
∴ , ,
∴ , ,
∴ , ,
∵将点A,B分别向下平移2个单位,再向左平移1个单位,分别得到点A,B的对应点C,D,
∴ , ,
∴ ;
(2)解:在y轴上存在一点M,使 ,设M坐标为 .
∵ ,
∴ ,
∴ ,
解得: 或 ,
∴ 或 ;
(3)解①当点P在线段 上移动时, ;
②当点P在 的延长线上时, ;
③当点P在 的延长线上时, .
解:当点P在线段BD上时,过点P作PE∥AB,
∵AB∥CD,
∴AB∥CD∥PE,
∴∠BAP=∠APE,∠EPO=∠DOP,
∴∠APO=∠APE+∠EPO=∠BAP+∠DOP;
当点P在BD的延长线上时,设CD与AP交于点E,
∵AB∥CD,
∴∠BAP=∠DEP,
∵∠DEP=∠DOP+∠APO,
∴∠BAP=∠DOP+∠APO;
当点P在DB的延长线上时,设AB与OP交于于点E,
∵AB∥CD,
∴∠PEB=∠DOP,
∵∠PEB=∠BAP+∠APO,
∴∠DOP=∠BAP+∠APO;
(1)利用几个非负数之和为0,则每一个数都为0,可得到关于a,b的方程组,即可得到a,b的值,可得到点A,B的坐标;利用点的坐标平移规律:上加下减(纵坐标),左减右加(横坐标),可得到点C,D的坐标;利用点的坐标,可求出四边形ACDB的面积.
(2)设点M的坐标为(0,m),利用已知条件可得到关于m的方程,解方程求出m的值,可得到点M的坐标.
(3)分情况讨论:当点P在线段BD上时,过点P作PE∥AB,利用平行线公理的推论可证得AB∥CD∥PE,利用平行线的性质可证得∠BAP=∠APE,∠EPO=∠DOP,根据∠APO=∠APE+∠EPO,可证得结论;当点P在BD的延长线上时,设CD与AP交于点E,利用平行线的性质可证得∠BAP=∠DEP,利用三角形的外角的性质可证得∠DEP=∠DOP+∠APO,据此可得到∠BAP、∠DOP、∠APO之间的数量关系;当点P在BD的延长线上时,设AB与OP交于于点E,利用平行线的性质可证得∠PEB=∠DOP,利用三角形的外角的性质可证得∠PEB=∠BAP+∠APO,据此可得到∠BAP、∠DOP、∠APO之间的数量关系.
26.(1)解:依题意,∠AOM=10t°,∠AOC=180°-∠AOM-∠COD=135°-10t°,
∵OB平分∠AOC,∴∠AOC=2∠AOB,即135°-10t°=2×60°,
解得t=1.5.
(2)解:①如图所示:
根据题意可得:∠AOM=10t°,
∴∠AOC=∠BOD=∠MON-∠AOM-∠COD=180°-10t°-45°=135°-10t°,
∵∠AOB=∠AOC+∠COD+∠BOD=60°,
∴45°+2(135°-10t°)=60°,
解得:t=12.75;
②如图所示:
根据题意可得:∠AOM=360°-10t°,
∴∠AOD=∠MON-∠AOM=180°-(360°-10t°)=10t°-180°,
∴∠AOC=∠BOD=∠AOD+∠COD=10t°-180°+45°=10t°-135°,
∴∠BOM=∠MON-∠BOD=180°-(10t°-135°)=315°-10t°,
∵∠AOB=∠BOM+∠AOM=60°,
∴315°-10t°+360°-10t°=60°,
解得:t=30.75;
综上,t的值为12.75或30.75;
故答案为:12.75或30.75;
(3)30°或150°
(3)①当OB的旋转角小于等于255°时,∠POQ=∠POC-∠QOC=∠AOC-∠BOC=30°;
②当OB的旋转角大于255°时,∠POQ=∠POC+∠QOC=∠AOC+∠BOC=150°;
综上,∠POQ的度数为30°或150°,
故答案为:30°或150°.
(1)先利用角的运算求出∠AOM=135°-10t°,再结合角平分线可得∠AOC=2∠AOB,即135°-10t°=2×60°,最后求出t的值即可;
(2)分类讨论,再分别画出图形并利用角的运算求解即可;
(3)分类讨论:①当OB的旋转角小于等于255°时,②当OB的旋转角大于255°时,再分别利用角的运算和等量代换求解即可.
2024-2025学年七年级上册期末临考猜题卷(苏科教版)
数学
考试范围:七上全册 考试时间:100分钟 分值:120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、单选题(每题2分,共16分)
1.下列各组数中,互为相反数的是( )
A.﹣2与|﹣2| B.﹣2与﹣|﹣2|
C.﹣2与﹣ D.2与|﹣2|
2.若实数在数轴上的位置如图所示,则化简的结果为( )
A. B. C. D.
3.定西市图书馆的建筑面积为16191平方米,阅览席有2000余个,馆藏各类文献资料共41.5万余册,数据41.5万用科学记数法表示应为( )
A. B. C. D.
4.如图,下列关于数m、n的说法正确的是( )
A.m>n B.m=n C.m>﹣n D.m=﹣n
5.如图,C 是线段AB 上一点,M是AC 的中点,N 是 BC 的中点,如果 MC 比 NC 长4 cm,那么 AC 比 BC长( )
A.8cm B.6 cm C.4 cm D.2cm
6.如图,∠AOC为直角,OC是∠BOD的平分线,且∠AOB=57.65°,则∠AOD的度数是( )
A.122°20' B.122°21' C.122°22' D.122°23'
7. 如图, 在正方形 中, 分别为 的中点, 为对角线 上的一个动点, 连结 , 则下列线段的长等于 最小值的是( )
A. B. C. D.
8.如图所示,在△ABC中,,,DE为AB的中垂线,,则CD的长是( )
A.3 B.4 C.6 D.8
二、填空题(每题2分,共16分)
9.若与是同类项,则 .
10.如图,,是其内部一条射线,以为一边作直角,点与点在边同侧,给出下列四个结论:①只与互余;②与互补;③平分,则平分;④的平分线与的平分线的夹角是直角.其中正确的是 (填序号).
11.多项式合并同类项后不含xy项,则k的值是 .
12.已知 是二元一次方程组 的解,则 .
13.已知 ,则 的值为 .
14.如图,已知点是正方形的边上的一个动点,连接,以为边作矩形,且边恰好经过点.若,则矩形的面积为 .
15.如图, 在 中, 是 的垂直平分线, 且分别交 于点 和 , , 则 .
16.设表示不超过x的最大整数{例如:请你认真理解的意义,当,若,则的值为 .
三、解答题(共10题,共68分)
17. 如图是由6个棱长都为1的小正方体搭成的几何体.
左视图 俯视图
(1)请在下面方格纸中分别画出它的左视图和俯视图;
(2)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的左视图和俯视图不变,那么最多可以添加 个小正方体.
先化简,再求值:,其中,.
19.计算
(1)
20.解下列方程:
(1)2(x-2)-3(4x-1)=5(1-x).
21.在正方形网格中,每个小正方形的边长都为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC向右平移3格,再向下平移2格,得到△DEF,使点A的对应点为点D,点B的对应点为点E,点C的对应点为点F.
(1)画出△DEF;
(2)在图中画出△ABC的AB边上的高线CG(保留利用格点的作图痕迹);
(3)△ABC的面积为 ;
(4)若AB的长为5,AB边上的高 .
22. 已知二元一次方程.
(1)写出此方程的所有正整数解.
(2)若二元一次方程组存在x,y互为相反数的解,请在横线处补上一个方程,并求出此方程组的解.
23.(1)如图,C为线段上一点,点B为的中点,且,求的长.
(2)如图,已知∠平分,若,求的度数.
24.如图,已知四点A,B,C,D,请用直尺按要求完成作图,
(1)作射线AD;
(2)作直线BC;
(3)连接BD,请在BD上确定点P,使的值最小,依据是 .
25.如图,在平面直为坐标系中,点A,B的坐标分别为,,且a、b满足,现同时将点A,B分别向下平移2个单位,再向左平移1个单位,分别得到点A,B的对应点C,D,连接,,.
(1)求点C,D的坐标及四边形的面积;
(2)在y轴上是否存在一点M,连接,,使?若存在这样一点,求出点M的坐标,若不存在,试说明理由;
(3)点P是直线上的一个动点,连接,,当点P在直线上移动时(不与B,D重合),直接写出,,之间满足的数量关系.
26. 如图 1,点O为直线MN上一点,将一副三角板摆放在直线MN同侧,将60°角的顶点与45°角的顶点重合放在点O处,三角板OAB的顶点A与三角板OCD的顶点D在直线MN上,三角板OCD保持不动,三角板OAB绕点O以每秒10°的速度顺时针旋转一周,设旋转时间为t s.
(1)如图2,当OB平分∠AOC时,求t的值;
(2)当∠AOC=∠BOD时,画出相应的图形,并求t的值;
(3)三角板OAB在旋转过程中,若OP平分∠AOC,OQ平分∠BOC,直接写出∠POQ的度数.
答案解析部分
1.A
解:A、﹣2与|﹣2|=2,互为相反数,故此选项符合题意;
B、﹣2与﹣|﹣2|=﹣2,两数相等,故此选项不符合题意;
C、﹣2与﹣ ,两数相加不为零,故此选项不符合题意;
D、2与|﹣2|=2,两数相等,故此选项不符合题意;
故答案为:A.
直接利用相反数的定义以及绝对值的性质化简进而得出答案.
2.C
3.C
解:41.5万.
故选:C.
本题主要考查科学记数法,根据科学记数法的表示方法求解即可.科学记数法的表示形式为的形式,其中a为整数,确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同,据此即可作答.
4.D
∵m和n在原点两侧,且到原点的距离相等,
∴m和n是互为相反数,即m=-n;
故答案为:D。
根据数轴上所表示的数的特点:原点右边表示正数,原点左边表示负数,右边的数总比左边的数大,互为相反数的两个数位于原点的两侧,到原点的距离相等,从而即可一一判断得出答案。
5.A
解:∵ M是AC 的中点,
∴AC=2MC=2AM,
∵N 是 BC 的中点,
∴BC=2CN=2BN.
∵MC-NC=4cm,
∴AC-BC=2MC-2CN=2(MC-NC)=8cm.
故答案为:A.
根据线段中点的定义可得AC=2MC=2AM,BC=2CN=2BN.最后代入AC-BC,即可得到答案.
6.B
7.D
解:连接CE,AP,如图,
点A,C关于BD对称,则AP+EP的最小值为EC,
设正方形的边长为2a,则DE=a,
∴ EC=,
∵ AB=2a,DE=a,BD=a,AF=a,
∴ AP+EP的最小值是AF的长.
故答案为:D.
根据正方形的性质和轴对称,可得AP+EP的最小值为EC,根据勾股定理可得EC和AF的长,即可求得.
8.C
9.4或
10.②③④
11.1
解:由题意可得:
=
∵不含xy项
∴2k-2=0
解得:k=1
故答案为:1
合并同类项,根据不含xy项,可得其系数为0,列出方程,解方程即可求出答案.
12.8
解:由题意得 ,
①+②得,m+3n=8.
13.3
解:由题意得:,
解得,
∴==3.
故答案为:3.
两个非负数之和等于0,则每个非负数等于0,依此列方程组求解,再代值计算即可.
14.
15.70°
解:∵∠B=60°,∠C=25°,
∴∠BAC=180°-∠B-∠C=95°.
∵DE是AC的垂直平分线,
∴AD=CD,
∴∠DAC=∠C=25°,
∴∠BAD=∠BAC-∠DAC=70°
故答案为:70°.
利用三角形内角和定理求得∠BAC,再利用线段垂直平分线的性质得DA=DC,继而可得∠DAC的度数,利用角的和差运算即可得到结论.
16.4
解: ,
,
又 表示不超过x的最大整数 ,
, ,,,等于0,或等于1,
,
, ,,,中应共有32个1,47个0,
= == =0, = ===1,
,,
解得:,
=4.
故答案为:4.
根据, 表示不超过x的最大整数 ,得到 , ,,,等于0,或等于1,再根据,可得到 , ,,,中应共有32个1,47个0,进而得到,,解得a的取值范围,即可求解.
17.(1)解:如图所示:
左视图 俯视图
(2)2
解:(1)如图所示:
(2)保持这个几何体的左视图和俯视图不变,那么最多可以添加2个,
故答案为:2.
(1)根据三视图的概念作图即可得出答案;
(2)保持这个几何体的左视图和俯视图不变,那么最多可以在后面一行第一列和第二列各添加一个小正方体即可。
18.解:
,
当,时,原式
先运用完全平方公式,平方差公式运算,并合并同类项,然后运用多项式除以单项式的法则解题,最后代入x,y即可解题.
19.(1)
(2)
(3)
(4)
20.(1)解:去括号得,2x-4-12x+3=5-5x,
移项得,2x-12x+5x=5+4-3,
合并同类项得,-5x=6,
系数化为1得,;
(2)解:去分母得,2(2x-1)-(x+5)=6(2x+1),
去括号得,4x-2-x-5=12x+6,
移项得,4x-x-12x=6+2+5,
合并同类项得,-9x=13,
系数化为1得,.
(1)先去括号,再移项,合并同类项,最后系数化为1,即可解方程;
(2)先去分母,再去括号,移项,最后合并同类项和系数化为1,即可解方程.
21.(1)解:如图,将△ABC的三个顶点分别向右平移3格,再向下平移2格,得到对应点的位置,顺次连接即可得到△DEF;
(2)解:如图,利用格点的特点,过C点作AB的垂线CN,交AB于点G,CG即为AB边上的高线;
(3)
(4)
解:(3)△ABC的面积为:,
故答案为:;
(4)由(3)得,
∴,
∵,
∴,
解得.
故答案为:.
(1)利用方格纸的特点,分别将点A、B、C向右平移3格,再向下平移2格可得点D、E、F的位置,然后顺次连接即可;
(2)过C点作AB的垂线CN,交AB于点G,CG即为AB边上的高线;
(3)利用方格纸的特点及割补法,用△ABC外接正方形的面积分别减去周围三个三角形的面积,即可求出△ABC的面积;
(4)直接根据三角形的面积公式结合(3)的结果可得CG的值.
22.(1)解:方程的正整数为:;
(2)解:方程组的解是互为相反数,
,
把代入得:
,
解得:,
,
,
括号处补的方程为:,
方程组为:,
①②得:,
把代入②得:,
方程组的解为:.
解:(1)∵2x+5y=24,
∴,
∵x、y都是正整数,
∴24-2x一定是5的倍数,
∴24-2x=20或24-2x=10,
∴x=2或x=7,
当x=2时,y=4;
当x=7时,y=2,
∴方程2x+5y=24的正整数解为;
(1)将2x+5y=24变形为用含x的式子表示y的形式,结合x、y都是正整数可得4-2x=20或24-2x=10,从而求解可求出x的值,进而代入即可求出y,即可得到方程的正整数解;
(2)根据方程组的解是互为相反数得到x=-y,将其代入2x+5y=24求出x,y的值,根据方程组解得定义即可得到括号处补的方程可为2x+3y=8;进而利用加减消元法解方程组,用①-②消去x求出y的值,再将y的值代入②可求出x的值,从而即可得到方程组的解.
23.解:(1)∵点B为的中点,,
又,
;
(2)设,则,
,
平分,
,
即,
,
.
(1)由点B为的中点,求得,结合和,即可求得的长,得到答案;
(2)设,得到,且,根据平分,得到,列出方程,求得方程的解,即可得到答案.
24.(1)解:射线AD是以点A为端点,延伸方向为AD方向,作射线如图所示
(2)解:直线BC向两方无限延伸,过点B,C作直线BC如图所示;
(3)两点之间,线段最短
(3)解:连接,交于点,这时最小,
理由:两点之间线段最短.
故答案为两点之间,线段最短.
(1)根据题意作射线AD即可;
(2)根据作直线的方法作图即可;
(3)根据两点之间线段最短求解即可。
25.(1)解:∵ ,
∴ , ,
∴ , ,
∴ , ,
∵将点A,B分别向下平移2个单位,再向左平移1个单位,分别得到点A,B的对应点C,D,
∴ , ,
∴ ;
(2)解:在y轴上存在一点M,使 ,设M坐标为 .
∵ ,
∴ ,
∴ ,
解得: 或 ,
∴ 或 ;
(3)解①当点P在线段 上移动时, ;
②当点P在 的延长线上时, ;
③当点P在 的延长线上时, .
解:当点P在线段BD上时,过点P作PE∥AB,
∵AB∥CD,
∴AB∥CD∥PE,
∴∠BAP=∠APE,∠EPO=∠DOP,
∴∠APO=∠APE+∠EPO=∠BAP+∠DOP;
当点P在BD的延长线上时,设CD与AP交于点E,
∵AB∥CD,
∴∠BAP=∠DEP,
∵∠DEP=∠DOP+∠APO,
∴∠BAP=∠DOP+∠APO;
当点P在DB的延长线上时,设AB与OP交于于点E,
∵AB∥CD,
∴∠PEB=∠DOP,
∵∠PEB=∠BAP+∠APO,
∴∠DOP=∠BAP+∠APO;
(1)利用几个非负数之和为0,则每一个数都为0,可得到关于a,b的方程组,即可得到a,b的值,可得到点A,B的坐标;利用点的坐标平移规律:上加下减(纵坐标),左减右加(横坐标),可得到点C,D的坐标;利用点的坐标,可求出四边形ACDB的面积.
(2)设点M的坐标为(0,m),利用已知条件可得到关于m的方程,解方程求出m的值,可得到点M的坐标.
(3)分情况讨论:当点P在线段BD上时,过点P作PE∥AB,利用平行线公理的推论可证得AB∥CD∥PE,利用平行线的性质可证得∠BAP=∠APE,∠EPO=∠DOP,根据∠APO=∠APE+∠EPO,可证得结论;当点P在BD的延长线上时,设CD与AP交于点E,利用平行线的性质可证得∠BAP=∠DEP,利用三角形的外角的性质可证得∠DEP=∠DOP+∠APO,据此可得到∠BAP、∠DOP、∠APO之间的数量关系;当点P在BD的延长线上时,设AB与OP交于于点E,利用平行线的性质可证得∠PEB=∠DOP,利用三角形的外角的性质可证得∠PEB=∠BAP+∠APO,据此可得到∠BAP、∠DOP、∠APO之间的数量关系.
26.(1)解:依题意,∠AOM=10t°,∠AOC=180°-∠AOM-∠COD=135°-10t°,
∵OB平分∠AOC,∴∠AOC=2∠AOB,即135°-10t°=2×60°,
解得t=1.5.
(2)解:①如图所示:
根据题意可得:∠AOM=10t°,
∴∠AOC=∠BOD=∠MON-∠AOM-∠COD=180°-10t°-45°=135°-10t°,
∵∠AOB=∠AOC+∠COD+∠BOD=60°,
∴45°+2(135°-10t°)=60°,
解得:t=12.75;
②如图所示:
根据题意可得:∠AOM=360°-10t°,
∴∠AOD=∠MON-∠AOM=180°-(360°-10t°)=10t°-180°,
∴∠AOC=∠BOD=∠AOD+∠COD=10t°-180°+45°=10t°-135°,
∴∠BOM=∠MON-∠BOD=180°-(10t°-135°)=315°-10t°,
∵∠AOB=∠BOM+∠AOM=60°,
∴315°-10t°+360°-10t°=60°,
解得:t=30.75;
综上,t的值为12.75或30.75;
故答案为:12.75或30.75;
(3)30°或150°
(3)①当OB的旋转角小于等于255°时,∠POQ=∠POC-∠QOC=∠AOC-∠BOC=30°;
②当OB的旋转角大于255°时,∠POQ=∠POC+∠QOC=∠AOC+∠BOC=150°;
综上,∠POQ的度数为30°或150°,
故答案为:30°或150°.
(1)先利用角的运算求出∠AOM=135°-10t°,再结合角平分线可得∠AOC=2∠AOB,即135°-10t°=2×60°,最后求出t的值即可;
(2)分类讨论,再分别画出图形并利用角的运算求解即可;
(3)分类讨论:①当OB的旋转角小于等于255°时,②当OB的旋转角大于255°时,再分别利用角的运算和等量代换求解即可.
同课章节目录
