2024-2025学年人教版八年级数学上册期末临考猜题卷 (含答案+解析)
文档属性
| 名称 | 2024-2025学年人教版八年级数学上册期末临考猜题卷 (含答案+解析) |  | |
| 格式 | docx | ||
| 文件大小 | 563.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-12 10:51:37 | ||
图片预览




文档简介
保密★启用前
2024-2025学年八年级上册期末临考猜题卷(人教版)
数学
考试范围:八上全册 考试时间:100分钟 分值:120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、单选题
1.如图,、为池塘岸边两点,小丽在池塘的一侧取一点,测得米,米,、间的距离不可能是( )
A.25米 B.27米 C.5米 D.4米
2.下列运算正确的是( )
A. B.
C. D.
3.下列运算正确的是( )
A.a3+ 2a3= 3a6 B.(a2)4=a6
C.a2·a3=a6 D.(a2b)2=a4b2
4.若将分式与分式通分后,分式的分母变为2(x﹣y)(x+y),则分式的分子应变为( )
A.6x2(x﹣y)2 B.2(x﹣y)
C.6x2 D.6x2(x+y)
5.将多项式加上一个整式,使它成为完全平方式,则下列不满足条件的整式是( )
A. B. C. D.
6.若点 和点 关于 轴对称,则点 在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.如图是用尺规作一个角等于已知角的示意图,根据,可得,则说明的依据是( )
A. B. C. D.
8.多边形的内角和为,那么从这个多边形的一个顶点引出的对角线的条数是( )
A.条 B.条 C.条 D.条
9.若,则下列分式化简中,正确的是( )
A. B. C. D.
10.如图 , 在等边三角形 的 边上各取一点 , 使 , 相交于点 . 若 , 则 点到 的距离等于( )
A.1 B.2 C. D.
二、填空题
11.分解因式:2a3b﹣8ab= .
12.已知,则代数式的值是 .
13.若代数式有意义,则x的满足的条件是 .
14.如图,将绕着点A顺时针旋转到的位置,使点E首次落在上.已知,,则 .
15.如图 , 这是某同学用纸板做成的一个底面直径为 、高为 的无底圆锥形玩具 (接缝忽略不计), 则做这个玩具所需纸板的面积是 (结果保留 ).
三、解答题
16.因式分解:
(1);
;
(3);
(4).
计算:
化简求值:.请你从中选择一个喜欢的数代入求值.
19.如图1,在等腰三角形ABC中,AB=AC,BD是边AC上的高线,CD=1,AD=4.点P是线段DA上的一点,作PE⊥BC于点E,连接DE.
(1)求AB= ,BC= .
(2)①当点P在线段AD上时,若△CDE是以CD为腰的等腰三角形,请求出所有符合条件的DP的长度.
②如图2,设PE交直线AB于点F,连接BP,若AF=3,求BP的长.
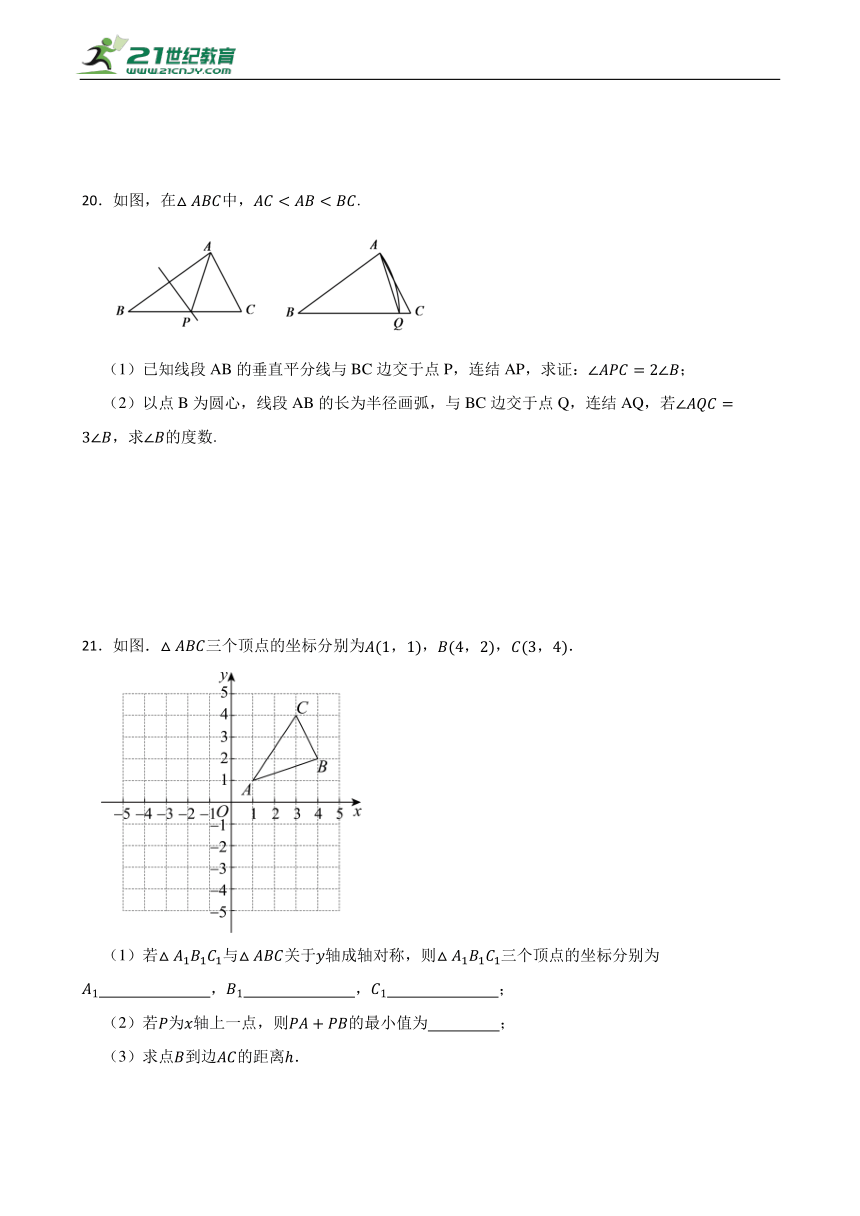
20.如图,在中,.
(1)已知线段AB的垂直平分线与BC边交于点P,连结AP,求证:;
(2)以点B为圆心,线段AB的长为半径画弧,与BC边交于点Q,连结AQ,若,求的度数.
21.如图.三个顶点的坐标分别为,,.
(1)若与关于轴成轴对称,则三个顶点的坐标分别为 , , ;
(2)若为轴上一点,则的最小值为 ;
(3)求点到边的距离.
22.如图1,边长为a的大正方形中有一个边长为b的小正方形,把图1中的阴影部分拼成如图2所示长方形.
(1)根据图1和图2的阴影部分的面积关系,可得等式________(用字母a,b表示)
(2)运用以上等式计算:
(3)如图3,100个圆由小到大套在一起,从外向里相间画阴影,最外面的圆的半径为100,向里依次为99,98,…,1,那么在这个图形中,所有阴影的面积和是多少?(结果保留)
答案解析部分
1.D
2.C
解:A、∵a3 a4=a7,∴A不符合题意;
B、∵(a3)2=a6,∴B不符合题意;
C、∵( 2a2)3= 8a6,∴C符合题意;
D、∵,∴D不符合题意.
故答案为:C.
利用同底数幂的乘法、幂的乘方、积的乘方和分式的约分的计算方法逐项分析判断即可.
3.D
解:∵①a3+2a3=3a3≠3a6,∴①错误;②(a2)4=a8≠a6,∴②错误;③a2.a3=a5≠a6,∴③错误;④(a2b)2=a4b2,∴④正确.
故正确答案选:D.
根据合并同类项法则,幂的乘方法则,同底数幂相乘的乘法法则和积的乘方的法则分别对各个选项判断即可得到正确的选项.
4.C
5.D
6.D
点A(a 2,3)和点B( 1,b+5)关于x轴对称,
得a 2=-1,b+5=-3.
解得a=1,b= 8.
则点C(a,b)在第四象限,
故答案为:D.
根据关于x轴对称的点的横坐标相等,纵坐标互为相反数,可得答案.
7.A
8.C
解:设此多边形的边数为x,
由题易得:(x-2)×180=1800,
解得x=12,
这个多边形的一个顶点出发所画的对角线条数为:12-3=9.
故答案为:C.
根据多边形内角和公式:n多边形内角和=(n-2)×180°,即可得到答案.
9.C
解:A、令x=2,y=3,则有,,等式不成立,不符合题意;
B、令x=2,y=3,则有,,等式不成立,不符合题意;
C、,正确,符合题意;
D、令x=2,y=3,则有,,等式不成立,不符合题意;
故答案为:C.
分式的基本性质:分式的分子和分母同时乘以或除以同一个不为0的整式,分式的值不变,据此解题即可.
10.C
解:如图,作,
是等边三角形,
,
,
,
,
,
,
,
,
,
.
故答案为:C.
由等边三角形的性质可得,再通过SAS判定,进而证得,然后利用三角形外角的性质求得 ,接着通过含角直角三角形的性质求得BD的长度,即 点到 的距离.
11.2ab(a+2)(a﹣2)
12.4
13.且
14.
15.
解:根据题意得:所需纸板的面积即圆锥的侧面积,
连接AB,过P作PO⊥AB于点O,如图:
∴AB=10cm,PO=12cm.
∵PA=PB,PO⊥AB,
∴AO=BO=5,
∴.
.
故答案为:.
连接AB,过P作PO⊥AB于点O,利用勾股定理求出PB长,根据侧面积=×弧长×半径=×底面周长×PB计算即可.
16.(1)
(2)
(3)
(4)
17.
18.解:原式=
=
=
当 时,原式 .
根据分式的四则混合运算,进行化简,再根据分母不为零,确定出x,代入求解即可.
19.(1)5;
(2)解:①分两种情况:
当DE =CD=1时, 则∠DEC =∠C,
∵PE⊥BC,
∴∠DEC+∠PED =∠PEC =90°,
∴∠C+∠CPE=90°,
∴∠CPE=∠PED,
∴PD=DE=1,
当CE=CD=1时,
在 和 中,
,
综上, 或
②分两种情况:
I.当P在线段AD上, 连接BP,
∵PE⊥BC,
∴∠EPC+∠C=90°, ∠BFE+∠FBE=90°,
∵AB=AC,
∴∠ABC=∠C,
∴∠EPC =∠BFE,
∵∠EPC=∠APF,
∴∠APF=∠AFP,
∴△APF是等腰三角形,
,
;
Ⅱ.当P在射线DA上, 连接BP,
同理可得.
,
综上,BP的长为 或
(1)∵AB=AC=AD+CD=1+4=5,
又∵BD⊥AC,
,
故答案为:5,;
(1)由勾股定理即可计算出BD的长,从而计算出BC的长;
(2)①分两种情况:当 时; 当时,分别进行求解即可;
②分两种情况:当P在线段AD上; 当P在射线DA上,进行计算即可求解.
20.(1)证明:∵点P在AB的垂直平分线上,所以PA=PB,
∴∠PAB=∠B,
∴∠APC=∠PAB+∠B=2∠B.
(2)解:根据题意,得BQ=BA,
∴∠BAQ=∠BQA,
设∠B=x,
∴∠AQC=∠B+∠BAQ=3x,
∴∠BAQ=∠BQA=2x,
在△ABQ中,x+2x+2x=180°,
解得x=36°,即∠B=36°.
(1)由线段垂直平分线的性质可得PA=PB,利用等边对等角可得∠PAB=∠B, 根据三角形外角的性质即可求解;
(2)由作图可知BQ=BA,利用等边对等角可得∠BAQ=∠BQA,则∠B=x,∠AQC=∠B+∠BAQ=3x, ∠BAQ=∠BQA=2x, 在△ABQ中,利用三角形内角和列出方程并解之即可.
21.(1);;
(2)
(3)解:∵的面积,
由勾股定理得,
∴,
∴ .
解:(1)依据题意画图如下:
, ,
故答案为: 、 、 。
(2)作出点的对称点,连接,则与轴的交点即是点的位置,如图所示:
则的最小值,
,
的最小值为;
(1)直接利用关于y轴对称点的性质得出对于点位置进而得出答案;
(2)如图所示作出点的对称点,连接,则与轴的交点即是点的位置,利用轴对称求最短路线的方法得出P点位置;
(3)利用割补法求的面积 ,由勾股定理得出AC的长,代入面积公式即可求出距离h.
22.(1)
(2)
(3)
2024-2025学年八年级上册期末临考猜题卷(人教版)
数学
考试范围:八上全册 考试时间:100分钟 分值:120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、单选题
1.如图,、为池塘岸边两点,小丽在池塘的一侧取一点,测得米,米,、间的距离不可能是( )
A.25米 B.27米 C.5米 D.4米
2.下列运算正确的是( )
A. B.
C. D.
3.下列运算正确的是( )
A.a3+ 2a3= 3a6 B.(a2)4=a6
C.a2·a3=a6 D.(a2b)2=a4b2
4.若将分式与分式通分后,分式的分母变为2(x﹣y)(x+y),则分式的分子应变为( )
A.6x2(x﹣y)2 B.2(x﹣y)
C.6x2 D.6x2(x+y)
5.将多项式加上一个整式,使它成为完全平方式,则下列不满足条件的整式是( )
A. B. C. D.
6.若点 和点 关于 轴对称,则点 在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.如图是用尺规作一个角等于已知角的示意图,根据,可得,则说明的依据是( )
A. B. C. D.
8.多边形的内角和为,那么从这个多边形的一个顶点引出的对角线的条数是( )
A.条 B.条 C.条 D.条
9.若,则下列分式化简中,正确的是( )
A. B. C. D.
10.如图 , 在等边三角形 的 边上各取一点 , 使 , 相交于点 . 若 , 则 点到 的距离等于( )
A.1 B.2 C. D.
二、填空题
11.分解因式:2a3b﹣8ab= .
12.已知,则代数式的值是 .
13.若代数式有意义,则x的满足的条件是 .
14.如图,将绕着点A顺时针旋转到的位置,使点E首次落在上.已知,,则 .
15.如图 , 这是某同学用纸板做成的一个底面直径为 、高为 的无底圆锥形玩具 (接缝忽略不计), 则做这个玩具所需纸板的面积是 (结果保留 ).
三、解答题
16.因式分解:
(1);
;
(3);
(4).
计算:
化简求值:.请你从中选择一个喜欢的数代入求值.
19.如图1,在等腰三角形ABC中,AB=AC,BD是边AC上的高线,CD=1,AD=4.点P是线段DA上的一点,作PE⊥BC于点E,连接DE.
(1)求AB= ,BC= .
(2)①当点P在线段AD上时,若△CDE是以CD为腰的等腰三角形,请求出所有符合条件的DP的长度.
②如图2,设PE交直线AB于点F,连接BP,若AF=3,求BP的长.
20.如图,在中,.
(1)已知线段AB的垂直平分线与BC边交于点P,连结AP,求证:;
(2)以点B为圆心,线段AB的长为半径画弧,与BC边交于点Q,连结AQ,若,求的度数.
21.如图.三个顶点的坐标分别为,,.
(1)若与关于轴成轴对称,则三个顶点的坐标分别为 , , ;
(2)若为轴上一点,则的最小值为 ;
(3)求点到边的距离.
22.如图1,边长为a的大正方形中有一个边长为b的小正方形,把图1中的阴影部分拼成如图2所示长方形.
(1)根据图1和图2的阴影部分的面积关系,可得等式________(用字母a,b表示)
(2)运用以上等式计算:
(3)如图3,100个圆由小到大套在一起,从外向里相间画阴影,最外面的圆的半径为100,向里依次为99,98,…,1,那么在这个图形中,所有阴影的面积和是多少?(结果保留)
答案解析部分
1.D
2.C
解:A、∵a3 a4=a7,∴A不符合题意;
B、∵(a3)2=a6,∴B不符合题意;
C、∵( 2a2)3= 8a6,∴C符合题意;
D、∵,∴D不符合题意.
故答案为:C.
利用同底数幂的乘法、幂的乘方、积的乘方和分式的约分的计算方法逐项分析判断即可.
3.D
解:∵①a3+2a3=3a3≠3a6,∴①错误;②(a2)4=a8≠a6,∴②错误;③a2.a3=a5≠a6,∴③错误;④(a2b)2=a4b2,∴④正确.
故正确答案选:D.
根据合并同类项法则,幂的乘方法则,同底数幂相乘的乘法法则和积的乘方的法则分别对各个选项判断即可得到正确的选项.
4.C
5.D
6.D
点A(a 2,3)和点B( 1,b+5)关于x轴对称,
得a 2=-1,b+5=-3.
解得a=1,b= 8.
则点C(a,b)在第四象限,
故答案为:D.
根据关于x轴对称的点的横坐标相等,纵坐标互为相反数,可得答案.
7.A
8.C
解:设此多边形的边数为x,
由题易得:(x-2)×180=1800,
解得x=12,
这个多边形的一个顶点出发所画的对角线条数为:12-3=9.
故答案为:C.
根据多边形内角和公式:n多边形内角和=(n-2)×180°,即可得到答案.
9.C
解:A、令x=2,y=3,则有,,等式不成立,不符合题意;
B、令x=2,y=3,则有,,等式不成立,不符合题意;
C、,正确,符合题意;
D、令x=2,y=3,则有,,等式不成立,不符合题意;
故答案为:C.
分式的基本性质:分式的分子和分母同时乘以或除以同一个不为0的整式,分式的值不变,据此解题即可.
10.C
解:如图,作,
是等边三角形,
,
,
,
,
,
,
,
,
,
.
故答案为:C.
由等边三角形的性质可得,再通过SAS判定,进而证得,然后利用三角形外角的性质求得 ,接着通过含角直角三角形的性质求得BD的长度,即 点到 的距离.
11.2ab(a+2)(a﹣2)
12.4
13.且
14.
15.
解:根据题意得:所需纸板的面积即圆锥的侧面积,
连接AB,过P作PO⊥AB于点O,如图:
∴AB=10cm,PO=12cm.
∵PA=PB,PO⊥AB,
∴AO=BO=5,
∴.
.
故答案为:.
连接AB,过P作PO⊥AB于点O,利用勾股定理求出PB长,根据侧面积=×弧长×半径=×底面周长×PB计算即可.
16.(1)
(2)
(3)
(4)
17.
18.解:原式=
=
=
当 时,原式 .
根据分式的四则混合运算,进行化简,再根据分母不为零,确定出x,代入求解即可.
19.(1)5;
(2)解:①分两种情况:
当DE =CD=1时, 则∠DEC =∠C,
∵PE⊥BC,
∴∠DEC+∠PED =∠PEC =90°,
∴∠C+∠CPE=90°,
∴∠CPE=∠PED,
∴PD=DE=1,
当CE=CD=1时,
在 和 中,
,
综上, 或
②分两种情况:
I.当P在线段AD上, 连接BP,
∵PE⊥BC,
∴∠EPC+∠C=90°, ∠BFE+∠FBE=90°,
∵AB=AC,
∴∠ABC=∠C,
∴∠EPC =∠BFE,
∵∠EPC=∠APF,
∴∠APF=∠AFP,
∴△APF是等腰三角形,
,
;
Ⅱ.当P在射线DA上, 连接BP,
同理可得.
,
综上,BP的长为 或
(1)∵AB=AC=AD+CD=1+4=5,
又∵BD⊥AC,
,
故答案为:5,;
(1)由勾股定理即可计算出BD的长,从而计算出BC的长;
(2)①分两种情况:当 时; 当时,分别进行求解即可;
②分两种情况:当P在线段AD上; 当P在射线DA上,进行计算即可求解.
20.(1)证明:∵点P在AB的垂直平分线上,所以PA=PB,
∴∠PAB=∠B,
∴∠APC=∠PAB+∠B=2∠B.
(2)解:根据题意,得BQ=BA,
∴∠BAQ=∠BQA,
设∠B=x,
∴∠AQC=∠B+∠BAQ=3x,
∴∠BAQ=∠BQA=2x,
在△ABQ中,x+2x+2x=180°,
解得x=36°,即∠B=36°.
(1)由线段垂直平分线的性质可得PA=PB,利用等边对等角可得∠PAB=∠B, 根据三角形外角的性质即可求解;
(2)由作图可知BQ=BA,利用等边对等角可得∠BAQ=∠BQA,则∠B=x,∠AQC=∠B+∠BAQ=3x, ∠BAQ=∠BQA=2x, 在△ABQ中,利用三角形内角和列出方程并解之即可.
21.(1);;
(2)
(3)解:∵的面积,
由勾股定理得,
∴,
∴ .
解:(1)依据题意画图如下:
, ,
故答案为: 、 、 。
(2)作出点的对称点,连接,则与轴的交点即是点的位置,如图所示:
则的最小值,
,
的最小值为;
(1)直接利用关于y轴对称点的性质得出对于点位置进而得出答案;
(2)如图所示作出点的对称点,连接,则与轴的交点即是点的位置,利用轴对称求最短路线的方法得出P点位置;
(3)利用割补法求的面积 ,由勾股定理得出AC的长,代入面积公式即可求出距离h.
22.(1)
(2)
(3)
同课章节目录
