湖北省黄石市阳新县2024-2025学年八年级上学期数学期末考试题 (含答案)
文档属性
| 名称 | 湖北省黄石市阳新县2024-2025学年八年级上学期数学期末考试题 (含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-13 00:00:00 | ||
图片预览



文档简介
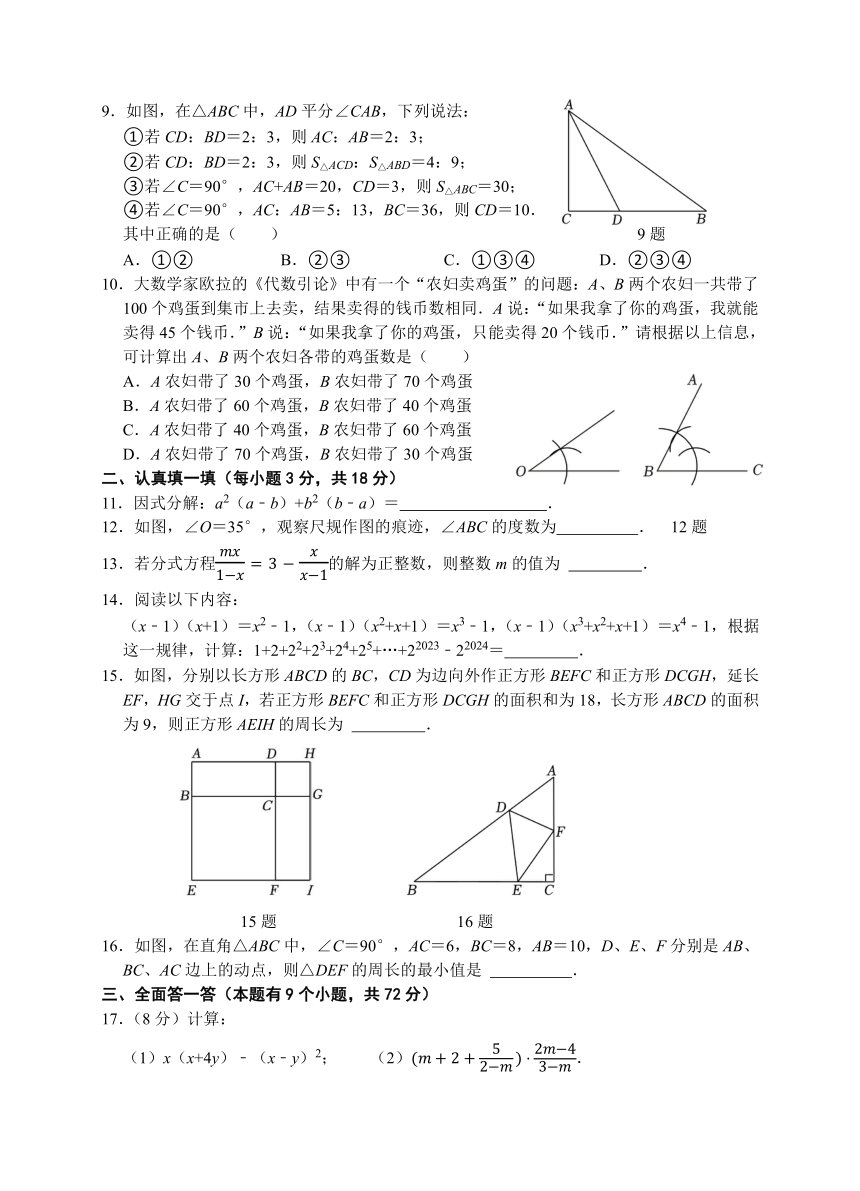
阳新县2024~2025学年度上学期期末质量检测
八年级数学试题卷
(考试时间:120分钟, 总分:120分)
注意事项:
1.答卷前,考生务必将自己的姓名、考试号填写在试题卷和答题卡上,并将考试号条形码粘贴在答题卡上的指定位置.
2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号,答在试题卷上无效.
3.非选择题(主观题)用0.5毫米的黑色签字笔直接答在答题卡上每题对应的答题区域内,答在试题卷上无效.作图一律用2B铅笔或0.5毫米黑色签字笔.
4.考生必须保持答题卡的整洁,考试结束后,请将答题卡上交.
一、仔细选一选(每小题3分,共30分)
1.下列图形中,对称轴最多的图形是( )
A.等腰三角形 B.等边三角形 C.正方形 D.正五边形
2.某校九年级学生计划前往湖北省博物馆开展一天的研学活动,出发前每班需要准备一个三角形形状的队旗,下列给出的三边长规格中,可以实现三角形队旗制作的是( )
A.6dm,6dm,12dm B. 6dm,8dm,7dm C.8dm,4dm,2dm D.6dm,3dm,10dm
3.下列计算正确的是( )
A.x3 x3=x9 B.a4÷2a3=2a C.2x2+3x3=5x5 D.(x5)2=x10
4.如图所示的网格是由9个相同的小正方形拼成的,图形的各个
顶点均为格点,则∠1﹣∠2﹣∠3的度数为( )
A.30° B.45° C.55° D.60°
5.若分式的值为0,则x的值为( )
A.3 B.3或﹣3 C.﹣3 D.0 4题
6.若a=20240,b=2025×2023﹣20242,,则下列a、b、c的大小关系正确的是( )
A.b<a<c B.a<b<c C.a<c<b D.c<b<a
7.如图,△ABC的面积为9cm2,BP平分∠ABC,AP⊥BP于P,
连接PC,则△PBC的面积为( )
A.3cm2 B.4cm2 C.4.5cm2 D.5cm2
8.若x2+2(m﹣3)x+1是完全平方式,x+n与x+2的乘积中 7题
不含x的一次项,则nm的值为( )
A.﹣4 B.16 C.﹣4或﹣16 D.4或16
9.如图,在△ABC中,AD平分∠CAB,下列说法:
①若CD:BD=2:3,则AC:AB=2:3;
②若CD:BD=2:3,则S△ACD:S△ABD=4:9;
③若∠C=90°,AC+AB=20,CD=3,则S△ABC=30;
④若∠C=90°,AC:AB=5:13,BC=36,则CD=10.
其中正确的是( ) 9题
A.①② B.②③ C.①③④ D.②③④
10.大数学家欧拉的《代数引论》中有一个“农妇卖鸡蛋”的问题:A、B两个农妇一共带了100个鸡蛋到集市上去卖,结果卖得的钱币数相同.A说:“如果我拿了你的鸡蛋,我就能卖得45个钱币.”B说:“如果我拿了你的鸡蛋,只能卖得20个钱币.”请根据以上信息,可计算出A、B两个农妇各带的鸡蛋数是( )
A.A农妇带了30个鸡蛋,B农妇带了70个鸡蛋
B.A农妇带了60个鸡蛋,B农妇带了40个鸡蛋
C.A农妇带了40个鸡蛋,B农妇带了60个鸡蛋
D.A农妇带了70个鸡蛋,B农妇带了30个鸡蛋
二、认真填一填(每小题3分,共18分)
11.因式分解:a2(a﹣b)+b2(b﹣a)= .
12.如图,∠O=35°,观察尺规作图的痕迹,∠ABC的度数为 . 12题
13.若分式方程的解为正整数,则整数m的值为 .
14.阅读以下内容:
(x﹣1)(x+1)=x2﹣1,(x﹣1)(x2+x+1)=x3﹣1,(x﹣1)(x3+x2+x+1)=x4﹣1,根据这一规律,计算:1+2+22+23+24+25+…+22023﹣22024= .
15.如图,分别以长方形ABCD的BC,CD为边向外作正方形BEFC和正方形DCGH,延长EF,HG交于点I,若正方形BEFC和正方形DCGH的面积和为18,长方形ABCD的面积为9,则正方形AEIH的周长为 .
15题 16题
16.如图,在直角△ABC中,∠C=90°,AC=6,BC=8,AB=10,D、E、F分别是AB、BC、AC边上的动点,则△DEF的周长的最小值是 .
三、全面答一答(本题有9个小题,共72分)
17.(8分)计算:
(1)x(x+4y)﹣(x﹣y)2; (2).
18.(7分)如图,点B,C分别在射线AM,AN上,点E,F都
在∠MAN内部的射线AD上,已知AB=AC,且∠BED=∠CFD=∠BAC.
(1)求证:△ABE≌△CAF;
(2)试判断EF,BE,CF之间的数量关系,并说明理由.
19.(7分)化简,再从﹣1,1,3中选择一个合适的数代入求值.
20.(7分)随着科技的发展,人工智能使生产生活更加便捷高效.某科技公司生产了一批新型搬运机器人,打出了如下的宣传:
根据该宣传,求新型机器人每天搬运的货物量.
21.(6分)如图,在8×8的正方形网格中,△ABC的三个顶点都在格点上,请按要求完成下列作图:①仅用无刻度直尺,且不能用直尺中的直角;②保留作图痕迹.
(1)在图甲中,画出△ABC的BC边上的中线AD.
(2)在图乙中,找一点P,连结线段BP,使得BP平分∠ABC.
22.(7分)对于多项式x3﹣5x2+x+10,我们把x=2代入此多项式,发现x=2能使多项式x3﹣5x2+x+10的值为0,由此可以断定多项式x3﹣5x2+x+10中有因式(x﹣2),(注:把x=a代入多项式,能使多项式的值为0,则多项式一定含有因式(x﹣a)),于是我们可以把多项式写成:x3﹣5x2+x+10=(x﹣2)(x2+mx+n),分别求出m、n后再代入x3﹣5x2+x+10=(x﹣2)(x2+mx+n),就可以把多项式x3﹣5x2+x+10因式分解.
(1)求式子中m、n的值;
(2)以上这种因式分解的方法叫“试根法”,用“试根法”分解多项式x3+5x2+8x+4.
23.(9分)大飞公司生产了一批A、B两种型号的产品,为了适应市场的不同消费需求,公司计划对两种产品进行精(包)装和简(包)装的方案:精装A型产品800台,精装B型产品的数量比精装A型产品的数量少,其余产品进行简装.
(1)求计划精装B型产品多少台?
(2)计划简装的产品数与这批产品总数之比为4:11,求这批产品共有多少台;
(3)(3)在(2)的条件下,经过市场调研发现精装的B型产品比精装的A型产品畅销,故公司决定调整包装方案,在保证精装产品总数量不变的情况下,减少A型产品精装的数量,增加B型产品精装的数量,结果是精装A型产品数量与简装A型产品数量的比为7:8,新增精装B型产品数量占总产品的,甲、乙两个包装工厂给出相同的价格,精装费用为10元/台,简装费用为8元/台,并推出如下优惠方案:
工厂 甲 乙
分类 精装 简装 A型 B型
优惠 10% 20% 10% 20%
那么公司选择哪一家包装工厂更划算?
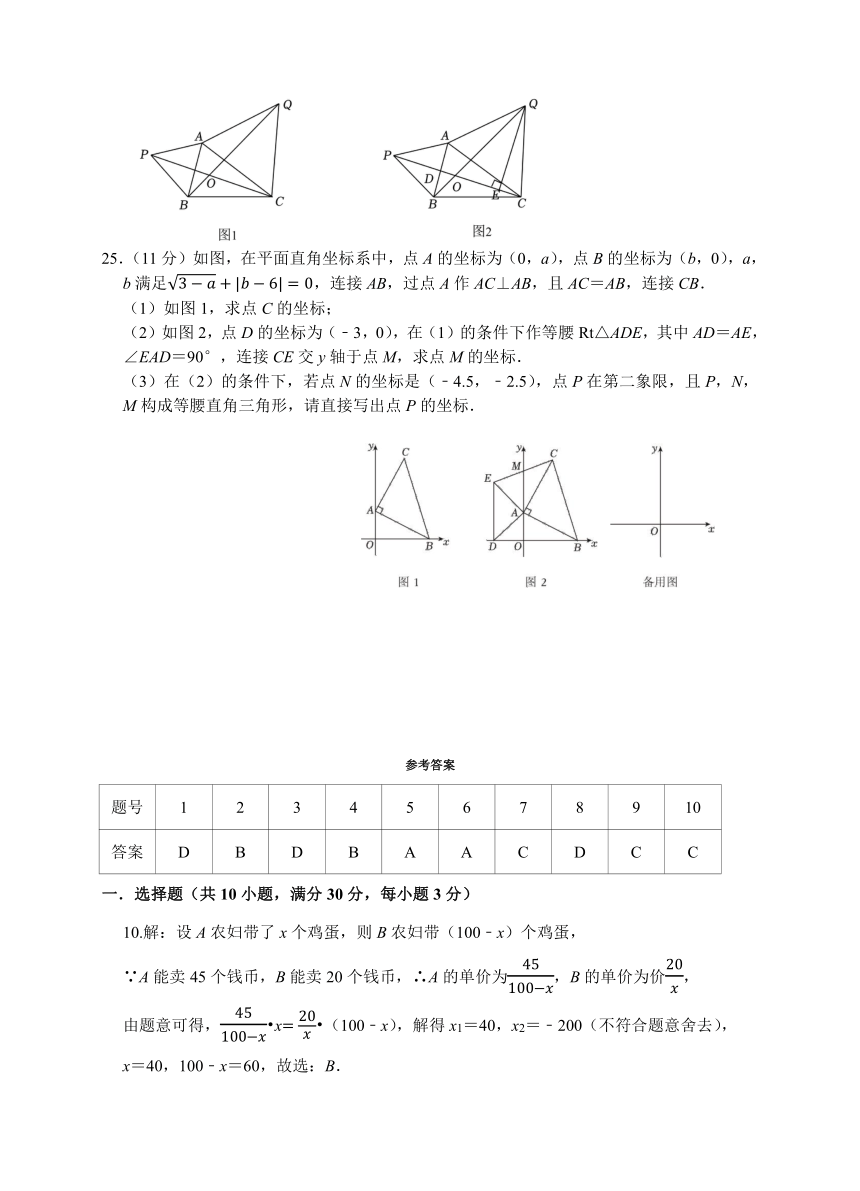
24.(10分)在锐角△ABC中,分别以AB,AC为边向外作等边△ABP和等边△ACQ,连接PC,BQ交于点O.
(1)如图1,易证△APC≌△ABQ,其依据是 ,从而得出结论:PC BQ与∠PBQ ∠PBA+∠APC(用“=”、“>”或“<”填空);
(2)如图2,若AC=BC,请探究线段PC与BQ的数量关系及直线PB与BQ的位置关系,并给出证明;
(3)在(2)的条件下,若PC交于AB于点D,QE⊥PC于点E(如图2),试探究DE,PD,CE之间存在的等量关系,并给予证明.
25.(11分)如图,在平面直角坐标系中,点A的坐标为(0,a),点B的坐标为(b,0),a,b满足,连接AB,过点A作AC⊥AB,且AC=AB,连接CB.
(1)如图1,求点C的坐标;
(2)如图2,点D的坐标为(﹣3,0),在(1)的条件下作等腰Rt△ADE,其中AD=AE,∠EAD=90°,连接CE交y轴于点M,求点M的坐标.
(3)在(2)的条件下,若点N的坐标是(﹣4.5,﹣2.5),点P在第二象限,且P,N,M构成等腰直角三角形,请直接写出点P的坐标.
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D B D B A A C D C C
一.选择题(共10小题,满分30分,每小题3分)
10.解:设A农妇带了x个鸡蛋,则B农妇带(100﹣x)个鸡蛋,
∵A能卖45个钱币,B能卖20个钱币,∴A的单价为,B的单价为价,
由题意可得, x (100﹣x),解得x1=40,x2=﹣200(不符合题意舍去),
x=40,100﹣x=60,故选:B.
二.填空题(共6小题,满分18分,每小题3分)
11. (a﹣b)2(a+b) . 12. 70° . 13. ﹣1 .
14. ﹣1 。 15. 24 . 16. 9.6 .
三.解答题(共9小题,满分72分,每小题8分)
17.(8分)计算:
解:(1)原式=x2+4xy﹣(x2﹣2xy+y2)……(2分)
=x2+4xy﹣x2+2xy﹣y2……(3分)
=6xy﹣y2;……(3分)
(2)原式 ……(2分)
……(3分)
=﹣2(m+3)……(3.5分)
=﹣2m﹣6.……(4分)
18.(7分)、
(1)证明:∵∠BED=∠BAE+∠ABE,∠BAC=∠BAE+∠CAF,……(1分)
∴∠ABE=∠CAF,同理:∠BAE=∠ACF,……(3分)
在△ABE和△CAF中,,∴△ABE≌△CAF(ASA);……(4分)
(2)EF+CF=BE,理由如下:……(5分)
∵△ABE≌△CAF,∴AE=CF,BE=AF,……(6分)
∵AE+EF=AF,∴CF+EF=BE.……(7分)
19.(7分)解:
……(2分)
……(3分)
……(4分)
,……(5分)
要使分式有意义,x+1≠0且x﹣3≠0,所以x不能为﹣1和3,取x=1,……(6分)
所以原式2.……(7分)
20.(7分)解:设每台新型机器人每天搬运的货物量为x吨,则每台旧型机器人每天搬运的货物量为(x﹣20)吨,……(1分)
由题意得:,解得:x=80,……(5分)
经检验,x=80是原方程的解,且符合题意,……(6分)
答:新型机器人每天搬运的货物量为80吨.……(7分)
21.(7分)解:(1)如图甲,取BC的中点D,连接AD,则AD即为所求.……(3分)
(2)由勾股定理得,AB5.
如图乙,在BC上取点D,使BD=AB=5,连接AD,取线段AD的中点P,连接BP,
则线段BP即为所求.……(6分)
22.(7分)解:(1)在等式x3﹣5x2+x+10=(x﹣2)(x2+mx+n),中,
分别令x=0,x=1,即可求出:m=﹣3,n=﹣5……(3分)
(2)把x=﹣1代入x3+5x2+8x+4,得其值为0,……(4分)
则多项式可分解为(x+1)(x2+ax+b)的形式,……(5分)
用上述方法可求得:a=4,b=4,……(6分)
所以x3+5x2+8x+4=(x+1)(x2+4x+4),
=(x+1)(x+2)2.……(7分)
解法二:把x=﹣2代入x3+5x2+8x+4,得其值为0,(本解法参照解法一评分)
则多项式可分解为(x+2)(x2+ax+b)的形式,
用上述方法可求得:a=3,b=2,
所以x3+5x2+8x+4=(x+2)(x2+3x+2),
=(x+1)(x+2)2.
23.(9分)解:(1)计划精装B型产品:(台);(2分)
(2)这批产品共有:(台);……(4分)
(3)计划精装B型产品:(台),……(5分)
精装A型产品数量:(台),
简装A型:(台),……(6分)
简装B型:2200﹣840﹣560﹣640=160(台),……(6.5分)
甲工厂:(840+560)×10×90%+(640+160)×8×80%=17720(元),……(7分)
乙工厂:(560×10+640×8)×90%+(840×10+160×8)×80%=17392(元),
因为17720>17392,所以选择乙工厂更划算.……(8.5分)
答:公司选择乙更划算.……(9分)
24.(10分)解:(1)∵△ABP和△ACQ是等边三角形,
∴AB=AP,AQ=AC,∠PAB=∠QAC=60°,
∴∠PAB+∠BAC=∠QAC+∠BAC,即∠PAC=∠BAQ,
在△PAC和△BAQ中,,∴△APC≌△ABQ(SAS),
∴PC=BQ,∠APC=∠ABQ,
∵∠PBQ=∠PBA+∠ABQ,∴∠PBQ=∠PBA+∠APC,
故答案为:SAS,=,=;……(3分)
(2)PC=BQ,PB⊥BQ,证明如下:……(3.5分)
同(1)得:△APC≌△ABQ(SAS),
∴PC=BQ,∠APC=∠ABQ,
∵△ABP是等边三角形,∴∠APB=∠ABP=60°,PA=PB,……(4分)
在△APC和△BPC中,,∴△APC≌△BPC(SSS),
∴∠APC=∠BPC∠APB=30°,……(5分)
∴∠ABQ=30°,∴∠PBQ=∠ABP+∠ABQ=60°+30°=90°,∴PB⊥BQ;……(6分)
(3)DE=PD+CE,证明如下:……(6.5分)
由(2)可知,PC=BQ,∠PBQ=90°,∠ABQ=30°,PC⊥AB,
∴∠BDO=90°,∴ODOB,∵QE⊥PC,∴∠QEO=90°,……(7分)
∵∠QOE=∠POB,∴∠OQE=∠BPC=30°,∴OEOQ,……(8分)
∴OD+OEOBOQ(OB+OQ)BQPC,即DEPC,……(9分)
∴PD+CEPC,∴DE=PD+CE.……(10分)
25.(11分)解:(1)∵,∴a=3,b=6,……(0.5分)
∴A点的坐标为(0,3),B点的坐标为(6,0),∴OA=3,OB=6,……(1分)
如图1,过点C作CH⊥y轴于H,
∵∠CAH+∠ACH=90°,∠CAH+∠OAB=90°,∴∠ACH=∠OAB,
在△ACH和△BAO中,,∴△ACH≌△BAO,……(2分)
∴AH=OB=6,HC=OA=3,∴OH=6,∴点C(3,9);……(3分)
(2)如图2,过点E作EG⊥y轴于点G,
同(1)理可证:△EGA≌△AOD,……(4分)
∴EG=AO=3,GA=OD=3,
∴EG=CH=3,GH=OH﹣OA﹣AG=3,
在△EGM和△CHM中,
,∴△EGM≌△CHM(AAS),∴GM=HM,……(5分)
∴,∴OM=OG+GM=6+=7.5,∴M(0,7.5);……(6分)
(3)点P坐标为(﹣14.5,2)或(﹣10,12)或(﹣7.25,4.75)
如图3,当PN=MN,∠PNM=90°时,过点N作NQ⊥y轴于Q,过点P作PF⊥NQ于F,
同理可证△PFN≌△NQM,
∴PF=NQ=4.5,FN=QM=2.5+7.5=10,
∴FQ=FN+NQ=10+4.5=14.5,
∴点P到y轴的距离为14.5,到x轴的距离为4.5﹣2.5=2,
∴点P(﹣14.5,2);……(7分)
如图4,当PM=MN,∠PMN=90°时,过点P作PR⊥y轴于R,过点N作NL⊥y轴于L,
同理可证△PMR≌△MNL,
∴NL=RM=4.5,RP=ML=10,
∴OR=RM+OM=4.5+7.5=12,∴点P(﹣10,12);……(9分)
如图5,当PM=PN,∠MPN=90°时,过点P作PT⊥x轴于T,过点M作MS⊥PT于S,过点N作NW⊥PT于W,
同理可证△PMS≌△PNW,∴PS=WN,SM=PW,
∵SM﹣WN=4.5,PS+PW=10,∴SM=PW=7.25,SP=WN=2.75,
∴PT=7.25﹣2.5=4.75,∴点P(﹣7.25,4.75),……(10分)
综上所述:点P坐标为P(﹣14.5,2)或(﹣10,12)或(﹣7.25,4.75).……(11分)
八年级数学试题卷
(考试时间:120分钟, 总分:120分)
注意事项:
1.答卷前,考生务必将自己的姓名、考试号填写在试题卷和答题卡上,并将考试号条形码粘贴在答题卡上的指定位置.
2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号,答在试题卷上无效.
3.非选择题(主观题)用0.5毫米的黑色签字笔直接答在答题卡上每题对应的答题区域内,答在试题卷上无效.作图一律用2B铅笔或0.5毫米黑色签字笔.
4.考生必须保持答题卡的整洁,考试结束后,请将答题卡上交.
一、仔细选一选(每小题3分,共30分)
1.下列图形中,对称轴最多的图形是( )
A.等腰三角形 B.等边三角形 C.正方形 D.正五边形
2.某校九年级学生计划前往湖北省博物馆开展一天的研学活动,出发前每班需要准备一个三角形形状的队旗,下列给出的三边长规格中,可以实现三角形队旗制作的是( )
A.6dm,6dm,12dm B. 6dm,8dm,7dm C.8dm,4dm,2dm D.6dm,3dm,10dm
3.下列计算正确的是( )
A.x3 x3=x9 B.a4÷2a3=2a C.2x2+3x3=5x5 D.(x5)2=x10
4.如图所示的网格是由9个相同的小正方形拼成的,图形的各个
顶点均为格点,则∠1﹣∠2﹣∠3的度数为( )
A.30° B.45° C.55° D.60°
5.若分式的值为0,则x的值为( )
A.3 B.3或﹣3 C.﹣3 D.0 4题
6.若a=20240,b=2025×2023﹣20242,,则下列a、b、c的大小关系正确的是( )
A.b<a<c B.a<b<c C.a<c<b D.c<b<a
7.如图,△ABC的面积为9cm2,BP平分∠ABC,AP⊥BP于P,
连接PC,则△PBC的面积为( )
A.3cm2 B.4cm2 C.4.5cm2 D.5cm2
8.若x2+2(m﹣3)x+1是完全平方式,x+n与x+2的乘积中 7题
不含x的一次项,则nm的值为( )
A.﹣4 B.16 C.﹣4或﹣16 D.4或16
9.如图,在△ABC中,AD平分∠CAB,下列说法:
①若CD:BD=2:3,则AC:AB=2:3;
②若CD:BD=2:3,则S△ACD:S△ABD=4:9;
③若∠C=90°,AC+AB=20,CD=3,则S△ABC=30;
④若∠C=90°,AC:AB=5:13,BC=36,则CD=10.
其中正确的是( ) 9题
A.①② B.②③ C.①③④ D.②③④
10.大数学家欧拉的《代数引论》中有一个“农妇卖鸡蛋”的问题:A、B两个农妇一共带了100个鸡蛋到集市上去卖,结果卖得的钱币数相同.A说:“如果我拿了你的鸡蛋,我就能卖得45个钱币.”B说:“如果我拿了你的鸡蛋,只能卖得20个钱币.”请根据以上信息,可计算出A、B两个农妇各带的鸡蛋数是( )
A.A农妇带了30个鸡蛋,B农妇带了70个鸡蛋
B.A农妇带了60个鸡蛋,B农妇带了40个鸡蛋
C.A农妇带了40个鸡蛋,B农妇带了60个鸡蛋
D.A农妇带了70个鸡蛋,B农妇带了30个鸡蛋
二、认真填一填(每小题3分,共18分)
11.因式分解:a2(a﹣b)+b2(b﹣a)= .
12.如图,∠O=35°,观察尺规作图的痕迹,∠ABC的度数为 . 12题
13.若分式方程的解为正整数,则整数m的值为 .
14.阅读以下内容:
(x﹣1)(x+1)=x2﹣1,(x﹣1)(x2+x+1)=x3﹣1,(x﹣1)(x3+x2+x+1)=x4﹣1,根据这一规律,计算:1+2+22+23+24+25+…+22023﹣22024= .
15.如图,分别以长方形ABCD的BC,CD为边向外作正方形BEFC和正方形DCGH,延长EF,HG交于点I,若正方形BEFC和正方形DCGH的面积和为18,长方形ABCD的面积为9,则正方形AEIH的周长为 .
15题 16题
16.如图,在直角△ABC中,∠C=90°,AC=6,BC=8,AB=10,D、E、F分别是AB、BC、AC边上的动点,则△DEF的周长的最小值是 .
三、全面答一答(本题有9个小题,共72分)
17.(8分)计算:
(1)x(x+4y)﹣(x﹣y)2; (2).
18.(7分)如图,点B,C分别在射线AM,AN上,点E,F都
在∠MAN内部的射线AD上,已知AB=AC,且∠BED=∠CFD=∠BAC.
(1)求证:△ABE≌△CAF;
(2)试判断EF,BE,CF之间的数量关系,并说明理由.
19.(7分)化简,再从﹣1,1,3中选择一个合适的数代入求值.
20.(7分)随着科技的发展,人工智能使生产生活更加便捷高效.某科技公司生产了一批新型搬运机器人,打出了如下的宣传:
根据该宣传,求新型机器人每天搬运的货物量.
21.(6分)如图,在8×8的正方形网格中,△ABC的三个顶点都在格点上,请按要求完成下列作图:①仅用无刻度直尺,且不能用直尺中的直角;②保留作图痕迹.
(1)在图甲中,画出△ABC的BC边上的中线AD.
(2)在图乙中,找一点P,连结线段BP,使得BP平分∠ABC.
22.(7分)对于多项式x3﹣5x2+x+10,我们把x=2代入此多项式,发现x=2能使多项式x3﹣5x2+x+10的值为0,由此可以断定多项式x3﹣5x2+x+10中有因式(x﹣2),(注:把x=a代入多项式,能使多项式的值为0,则多项式一定含有因式(x﹣a)),于是我们可以把多项式写成:x3﹣5x2+x+10=(x﹣2)(x2+mx+n),分别求出m、n后再代入x3﹣5x2+x+10=(x﹣2)(x2+mx+n),就可以把多项式x3﹣5x2+x+10因式分解.
(1)求式子中m、n的值;
(2)以上这种因式分解的方法叫“试根法”,用“试根法”分解多项式x3+5x2+8x+4.
23.(9分)大飞公司生产了一批A、B两种型号的产品,为了适应市场的不同消费需求,公司计划对两种产品进行精(包)装和简(包)装的方案:精装A型产品800台,精装B型产品的数量比精装A型产品的数量少,其余产品进行简装.
(1)求计划精装B型产品多少台?
(2)计划简装的产品数与这批产品总数之比为4:11,求这批产品共有多少台;
(3)(3)在(2)的条件下,经过市场调研发现精装的B型产品比精装的A型产品畅销,故公司决定调整包装方案,在保证精装产品总数量不变的情况下,减少A型产品精装的数量,增加B型产品精装的数量,结果是精装A型产品数量与简装A型产品数量的比为7:8,新增精装B型产品数量占总产品的,甲、乙两个包装工厂给出相同的价格,精装费用为10元/台,简装费用为8元/台,并推出如下优惠方案:
工厂 甲 乙
分类 精装 简装 A型 B型
优惠 10% 20% 10% 20%
那么公司选择哪一家包装工厂更划算?
24.(10分)在锐角△ABC中,分别以AB,AC为边向外作等边△ABP和等边△ACQ,连接PC,BQ交于点O.
(1)如图1,易证△APC≌△ABQ,其依据是 ,从而得出结论:PC BQ与∠PBQ ∠PBA+∠APC(用“=”、“>”或“<”填空);
(2)如图2,若AC=BC,请探究线段PC与BQ的数量关系及直线PB与BQ的位置关系,并给出证明;
(3)在(2)的条件下,若PC交于AB于点D,QE⊥PC于点E(如图2),试探究DE,PD,CE之间存在的等量关系,并给予证明.
25.(11分)如图,在平面直角坐标系中,点A的坐标为(0,a),点B的坐标为(b,0),a,b满足,连接AB,过点A作AC⊥AB,且AC=AB,连接CB.
(1)如图1,求点C的坐标;
(2)如图2,点D的坐标为(﹣3,0),在(1)的条件下作等腰Rt△ADE,其中AD=AE,∠EAD=90°,连接CE交y轴于点M,求点M的坐标.
(3)在(2)的条件下,若点N的坐标是(﹣4.5,﹣2.5),点P在第二象限,且P,N,M构成等腰直角三角形,请直接写出点P的坐标.
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D B D B A A C D C C
一.选择题(共10小题,满分30分,每小题3分)
10.解:设A农妇带了x个鸡蛋,则B农妇带(100﹣x)个鸡蛋,
∵A能卖45个钱币,B能卖20个钱币,∴A的单价为,B的单价为价,
由题意可得, x (100﹣x),解得x1=40,x2=﹣200(不符合题意舍去),
x=40,100﹣x=60,故选:B.
二.填空题(共6小题,满分18分,每小题3分)
11. (a﹣b)2(a+b) . 12. 70° . 13. ﹣1 .
14. ﹣1 。 15. 24 . 16. 9.6 .
三.解答题(共9小题,满分72分,每小题8分)
17.(8分)计算:
解:(1)原式=x2+4xy﹣(x2﹣2xy+y2)……(2分)
=x2+4xy﹣x2+2xy﹣y2……(3分)
=6xy﹣y2;……(3分)
(2)原式 ……(2分)
……(3分)
=﹣2(m+3)……(3.5分)
=﹣2m﹣6.……(4分)
18.(7分)、
(1)证明:∵∠BED=∠BAE+∠ABE,∠BAC=∠BAE+∠CAF,……(1分)
∴∠ABE=∠CAF,同理:∠BAE=∠ACF,……(3分)
在△ABE和△CAF中,,∴△ABE≌△CAF(ASA);……(4分)
(2)EF+CF=BE,理由如下:……(5分)
∵△ABE≌△CAF,∴AE=CF,BE=AF,……(6分)
∵AE+EF=AF,∴CF+EF=BE.……(7分)
19.(7分)解:
……(2分)
……(3分)
……(4分)
,……(5分)
要使分式有意义,x+1≠0且x﹣3≠0,所以x不能为﹣1和3,取x=1,……(6分)
所以原式2.……(7分)
20.(7分)解:设每台新型机器人每天搬运的货物量为x吨,则每台旧型机器人每天搬运的货物量为(x﹣20)吨,……(1分)
由题意得:,解得:x=80,……(5分)
经检验,x=80是原方程的解,且符合题意,……(6分)
答:新型机器人每天搬运的货物量为80吨.……(7分)
21.(7分)解:(1)如图甲,取BC的中点D,连接AD,则AD即为所求.……(3分)
(2)由勾股定理得,AB5.
如图乙,在BC上取点D,使BD=AB=5,连接AD,取线段AD的中点P,连接BP,
则线段BP即为所求.……(6分)
22.(7分)解:(1)在等式x3﹣5x2+x+10=(x﹣2)(x2+mx+n),中,
分别令x=0,x=1,即可求出:m=﹣3,n=﹣5……(3分)
(2)把x=﹣1代入x3+5x2+8x+4,得其值为0,……(4分)
则多项式可分解为(x+1)(x2+ax+b)的形式,……(5分)
用上述方法可求得:a=4,b=4,……(6分)
所以x3+5x2+8x+4=(x+1)(x2+4x+4),
=(x+1)(x+2)2.……(7分)
解法二:把x=﹣2代入x3+5x2+8x+4,得其值为0,(本解法参照解法一评分)
则多项式可分解为(x+2)(x2+ax+b)的形式,
用上述方法可求得:a=3,b=2,
所以x3+5x2+8x+4=(x+2)(x2+3x+2),
=(x+1)(x+2)2.
23.(9分)解:(1)计划精装B型产品:(台);(2分)
(2)这批产品共有:(台);……(4分)
(3)计划精装B型产品:(台),……(5分)
精装A型产品数量:(台),
简装A型:(台),……(6分)
简装B型:2200﹣840﹣560﹣640=160(台),……(6.5分)
甲工厂:(840+560)×10×90%+(640+160)×8×80%=17720(元),……(7分)
乙工厂:(560×10+640×8)×90%+(840×10+160×8)×80%=17392(元),
因为17720>17392,所以选择乙工厂更划算.……(8.5分)
答:公司选择乙更划算.……(9分)
24.(10分)解:(1)∵△ABP和△ACQ是等边三角形,
∴AB=AP,AQ=AC,∠PAB=∠QAC=60°,
∴∠PAB+∠BAC=∠QAC+∠BAC,即∠PAC=∠BAQ,
在△PAC和△BAQ中,,∴△APC≌△ABQ(SAS),
∴PC=BQ,∠APC=∠ABQ,
∵∠PBQ=∠PBA+∠ABQ,∴∠PBQ=∠PBA+∠APC,
故答案为:SAS,=,=;……(3分)
(2)PC=BQ,PB⊥BQ,证明如下:……(3.5分)
同(1)得:△APC≌△ABQ(SAS),
∴PC=BQ,∠APC=∠ABQ,
∵△ABP是等边三角形,∴∠APB=∠ABP=60°,PA=PB,……(4分)
在△APC和△BPC中,,∴△APC≌△BPC(SSS),
∴∠APC=∠BPC∠APB=30°,……(5分)
∴∠ABQ=30°,∴∠PBQ=∠ABP+∠ABQ=60°+30°=90°,∴PB⊥BQ;……(6分)
(3)DE=PD+CE,证明如下:……(6.5分)
由(2)可知,PC=BQ,∠PBQ=90°,∠ABQ=30°,PC⊥AB,
∴∠BDO=90°,∴ODOB,∵QE⊥PC,∴∠QEO=90°,……(7分)
∵∠QOE=∠POB,∴∠OQE=∠BPC=30°,∴OEOQ,……(8分)
∴OD+OEOBOQ(OB+OQ)BQPC,即DEPC,……(9分)
∴PD+CEPC,∴DE=PD+CE.……(10分)
25.(11分)解:(1)∵,∴a=3,b=6,……(0.5分)
∴A点的坐标为(0,3),B点的坐标为(6,0),∴OA=3,OB=6,……(1分)
如图1,过点C作CH⊥y轴于H,
∵∠CAH+∠ACH=90°,∠CAH+∠OAB=90°,∴∠ACH=∠OAB,
在△ACH和△BAO中,,∴△ACH≌△BAO,……(2分)
∴AH=OB=6,HC=OA=3,∴OH=6,∴点C(3,9);……(3分)
(2)如图2,过点E作EG⊥y轴于点G,
同(1)理可证:△EGA≌△AOD,……(4分)
∴EG=AO=3,GA=OD=3,
∴EG=CH=3,GH=OH﹣OA﹣AG=3,
在△EGM和△CHM中,
,∴△EGM≌△CHM(AAS),∴GM=HM,……(5分)
∴,∴OM=OG+GM=6+=7.5,∴M(0,7.5);……(6分)
(3)点P坐标为(﹣14.5,2)或(﹣10,12)或(﹣7.25,4.75)
如图3,当PN=MN,∠PNM=90°时,过点N作NQ⊥y轴于Q,过点P作PF⊥NQ于F,
同理可证△PFN≌△NQM,
∴PF=NQ=4.5,FN=QM=2.5+7.5=10,
∴FQ=FN+NQ=10+4.5=14.5,
∴点P到y轴的距离为14.5,到x轴的距离为4.5﹣2.5=2,
∴点P(﹣14.5,2);……(7分)
如图4,当PM=MN,∠PMN=90°时,过点P作PR⊥y轴于R,过点N作NL⊥y轴于L,
同理可证△PMR≌△MNL,
∴NL=RM=4.5,RP=ML=10,
∴OR=RM+OM=4.5+7.5=12,∴点P(﹣10,12);……(9分)
如图5,当PM=PN,∠MPN=90°时,过点P作PT⊥x轴于T,过点M作MS⊥PT于S,过点N作NW⊥PT于W,
同理可证△PMS≌△PNW,∴PS=WN,SM=PW,
∵SM﹣WN=4.5,PS+PW=10,∴SM=PW=7.25,SP=WN=2.75,
∴PT=7.25﹣2.5=4.75,∴点P(﹣7.25,4.75),……(10分)
综上所述:点P坐标为P(﹣14.5,2)或(﹣10,12)或(﹣7.25,4.75).……(11分)
同课章节目录
