1.2整式的乘法 第1课时 单项式乘单项式 课件(共19张PPT)
文档属性
| 名称 | 1.2整式的乘法 第1课时 单项式乘单项式 课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-12 18:50:34 | ||
图片预览





文档简介
(共19张PPT)
1.2 整式的乘法
第1课时 单项式乘单项式
1. 掌握单项式与单项式相乘的运算法则;(重点)
2. 能够灵活地进行单项式与单项式相乘的运算.(难点)
D
C
B
A
a
3b
2b
3a
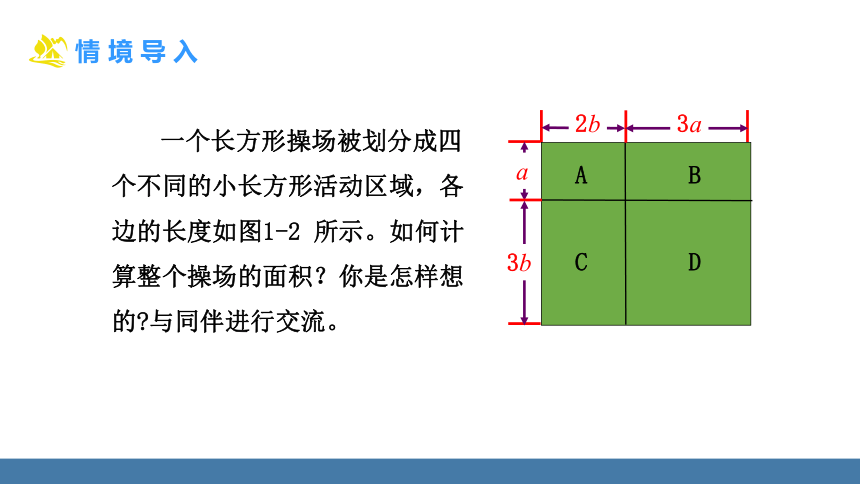
一个长方形操场被划分成四个不同的小长方形活动区域,各边的长度如图1-2 所示。如何计算整个操场的面积?你是怎样想的 与同伴进行交流。
D
C
B
A
a
3b
2b
3a
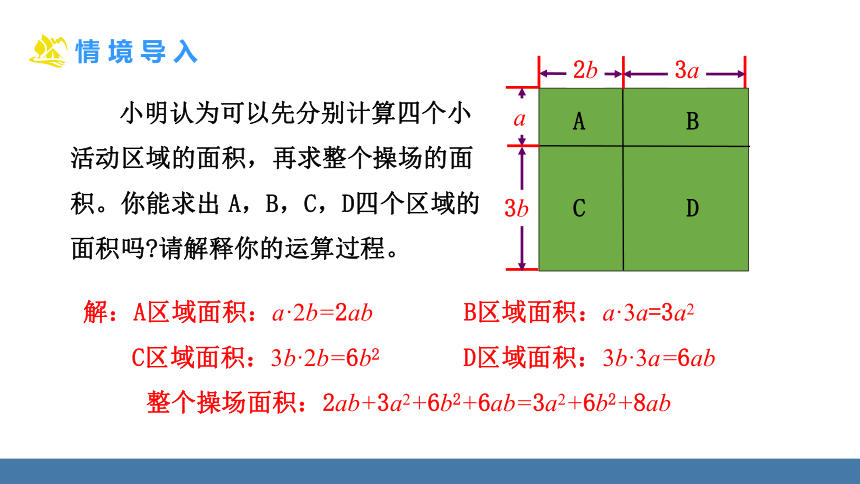
小明认为可以先分别计算四个小活动区域的面积,再求整个操场的面积。你能求出 A,B,C,D四个区域的面积吗 请解释你的运算过程。
解:A区域面积:a·2b=2ab B区域面积:a·3a=3a2
C区域面积:3b·2b=6b2 D区域面积:3b·3a=6ab
整个操场面积:2ab+3a2+6b2+6ab=3a2+6b2+8ab
(1)你能计算abc·b2c,3x2y·2xy3,5a2b2·(-2ab)吗?
在你探索单项式乘法运算法则的过程中,运用了哪些运算律和运算法则?
abc·b2c
=a·(b·b2)·(c·c)
=ab3c2.
3x2y·2xy3
=(3·2)·(x2·x)(y·y3)
=6x3y4.
运用了乘法交换律和结合律.
5a2b2·(-2ab)
=[5·(-2)]·(a2·a)·(b2·b)
=-10a3b3
如何进行单项式乘单项式的运算?
单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,其余字母连同它的指数不变,作为积的因式.
注意:(1)系数相乘;
(2)相同字母的幂相乘;
(3)其余字母连同它的指数不变,作为积的因式.
单项式与单项式的乘法法则
(2)原式=[(-2)×(-3)] (a2a) b3 =6a3b3;
(3)原式=7xy2z 4x2y2z2
=(7×4) (xx2) (y2y2) (zz2)
=28x3y4z3;
(4)原式=[(-3)××(-2)] (aa2a) (bb) (cc3)
=2a4b2c4
多个单项式相乘方法同样适用且结果仍为单项式
例1 计算:
(1)2xy2 xy; (2)-2a2b3 (-3a);
(3)7xy2z (2xyz)2; (4)(-3ab) a2c (-2abc3)
解:(1)原式=(2×) (x x) (y2 y)=;
单项式乘单项式的几点注意:
(1)在计算时,应先进行符号运算,积的系数等于各因式系数的积.
(2)注意按运算顺序计算,若有乘方,先算乘方.
(3)只在一个单项式里含有的字母,最后不要漏乘.
(4)单项式的法则适用于三个及以上的单项式相乘.
1.计算:
(1) 5x2 ·2x2y ; (2)4y ·(–2xy2);
(3) -3ab ·(-4b2) ; (4)(-ab3)(2abc2)(a2c)3.
解:(1)原式=(5×2)(x2·x2)y=10x4y;
(2)原式=[4×(–2)](y·y2) ·x= –8xy3;
(3)原式=[(-3)×(-4)](b·b2)a=12ab3;
(4)原式= –ab3·2abc2·a6c3
=[(–1)×2×1](a·a·a6)(b3·b)(c2·c3)= –2a8b4c5
a
a
a
a
如图,一幅边长为 a m 的正方形风景画,上下各留有 a m 的空白区域作装饰,中间画面的面积是多少平方米?
解:a a-2 a a=a2-a2=a2(平方米)
所以,中间画面的面积是a2平方米.
例2 已知一个长方体包装箱,长为3a m,宽为2b m,高为ab m.
(1)求这个包装箱的体积;
(2)如果给这个包装箱的外表面都喷上油漆,那么共需喷多少平方米的油漆
解:因为3a·2b·ab=6a2b2(m3),
所以这个包装箱的体积为6a2b2 m3.
解:包装箱的表面积为2(3a·2b+3a·ab+2b·ab)=(12ab+6a2b+4ab2)m2,
所以共需喷(12ab+6a2b+4ab2)m2的油漆.
例3 已知-2x3m+1y2n与7xy2的积与x5y8是同类项,求m2+n的值.
所以m2+n=12+3=1+3=4.
解:因为-2x3m+1y2n与7xy2的积与x5y8是同类项,
解:长方形的面积是xym2,
则绿化的面积是 x×y=xy(m2),
所以剩下的面积是xy-xy=xy(m2).
2.有一块长为xm,宽为ym的长方形空地,现在要在这块地中规划一块长xm,宽ym的长方形空地用于绿化,求绿化的面积和剩下的面积.
2.计算3a·(-2a)2的结果为 ( )
A.-12a3 B.-6a2 C.12a3 D.6a2
1.计算2a·ab的结果是 ( )
A.2ab B.2a2b C.3ab D.3a2b
B
C
B
3.小刘做了四道题目:①3x3y·2xyz2=5x4y2z2;②2a2·(-3a)3=-54a6;
③(-m2n)2·(-8mn2)=-2m5n4;④-3a3b·(-3ab)=9a4b2.他做对的题目是
( )
A.①② B.③④
C.①②③ D.②③④
5.若(-5am+1b2n-1)·2ab3=-10a4b4,则m-n的值为 ( )
A.-3 B.-1
C.1 D.3
4.一块长方形草坪的长是3xa+1 m,宽是2xb-1 m(a,b均为大于1的正整数),则长方形草坪的面积是 ( )
A.6xa-b m2 B.6xa+b m2
C.6xa+b-1 m2 D.6xa+b-2 m2
B
C
5.计算:
(1)4xy2z·(-0.5x2y)3; (2)3a2·(-ab)·(-2a2b)3;
(3)(-a4b)3·a-(2a4b)2·(-a5b).
解:(1)原式=4xy2z·(-x6y3)
=-x7y5z.
(2)原式=3a2·(-ab)·(-8a6b3)
=3a9b4.
(3)原式=(-a12b3)·a-4a8b2·(-a5b)
=-a13b3+3a13b3
=2a13b3.
解:5a·(2a+a)-2a(5a-3a)
=5a·3a-2a·2a
=15a2-4a2
=11a2.
故阴影部分的面积为11a2.
6.求图中阴影部分的面积.(列式写过程)
7.已知9an-6b-2-n与-2a3m+1b2n的积与5a4b是同类项,求(m-n)2024的值.
解:因为9an-6b-2-n与-2a3m+1b2n的积与5a4b是同类项,
所以-2-n+2n=1,n-6+3m+1=4,
解得n=3,m=2,
所以(m-n)2024=(2-3)2024=1.
单项式乘单项式法则
整式的
乘法
单项式与单项式相乘,把它们的系数、同底数幂分别相乘,其余字母连同它的指数不变,作为积的因式.
一系数相乘;
二相同字母的幂相乘;
三其余字母连同它的指数不变,作为积的因式.
步骤
1.2 整式的乘法
第1课时 单项式乘单项式
1. 掌握单项式与单项式相乘的运算法则;(重点)
2. 能够灵活地进行单项式与单项式相乘的运算.(难点)
D
C
B
A
a
3b
2b
3a
一个长方形操场被划分成四个不同的小长方形活动区域,各边的长度如图1-2 所示。如何计算整个操场的面积?你是怎样想的 与同伴进行交流。
D
C
B
A
a
3b
2b
3a
小明认为可以先分别计算四个小活动区域的面积,再求整个操场的面积。你能求出 A,B,C,D四个区域的面积吗 请解释你的运算过程。
解:A区域面积:a·2b=2ab B区域面积:a·3a=3a2
C区域面积:3b·2b=6b2 D区域面积:3b·3a=6ab
整个操场面积:2ab+3a2+6b2+6ab=3a2+6b2+8ab
(1)你能计算abc·b2c,3x2y·2xy3,5a2b2·(-2ab)吗?
在你探索单项式乘法运算法则的过程中,运用了哪些运算律和运算法则?
abc·b2c
=a·(b·b2)·(c·c)
=ab3c2.
3x2y·2xy3
=(3·2)·(x2·x)(y·y3)
=6x3y4.
运用了乘法交换律和结合律.
5a2b2·(-2ab)
=[5·(-2)]·(a2·a)·(b2·b)
=-10a3b3
如何进行单项式乘单项式的运算?
单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,其余字母连同它的指数不变,作为积的因式.
注意:(1)系数相乘;
(2)相同字母的幂相乘;
(3)其余字母连同它的指数不变,作为积的因式.
单项式与单项式的乘法法则
(2)原式=[(-2)×(-3)] (a2a) b3 =6a3b3;
(3)原式=7xy2z 4x2y2z2
=(7×4) (xx2) (y2y2) (zz2)
=28x3y4z3;
(4)原式=[(-3)××(-2)] (aa2a) (bb) (cc3)
=2a4b2c4
多个单项式相乘方法同样适用且结果仍为单项式
例1 计算:
(1)2xy2 xy; (2)-2a2b3 (-3a);
(3)7xy2z (2xyz)2; (4)(-3ab) a2c (-2abc3)
解:(1)原式=(2×) (x x) (y2 y)=;
单项式乘单项式的几点注意:
(1)在计算时,应先进行符号运算,积的系数等于各因式系数的积.
(2)注意按运算顺序计算,若有乘方,先算乘方.
(3)只在一个单项式里含有的字母,最后不要漏乘.
(4)单项式的法则适用于三个及以上的单项式相乘.
1.计算:
(1) 5x2 ·2x2y ; (2)4y ·(–2xy2);
(3) -3ab ·(-4b2) ; (4)(-ab3)(2abc2)(a2c)3.
解:(1)原式=(5×2)(x2·x2)y=10x4y;
(2)原式=[4×(–2)](y·y2) ·x= –8xy3;
(3)原式=[(-3)×(-4)](b·b2)a=12ab3;
(4)原式= –ab3·2abc2·a6c3
=[(–1)×2×1](a·a·a6)(b3·b)(c2·c3)= –2a8b4c5
a
a
a
a
如图,一幅边长为 a m 的正方形风景画,上下各留有 a m 的空白区域作装饰,中间画面的面积是多少平方米?
解:a a-2 a a=a2-a2=a2(平方米)
所以,中间画面的面积是a2平方米.
例2 已知一个长方体包装箱,长为3a m,宽为2b m,高为ab m.
(1)求这个包装箱的体积;
(2)如果给这个包装箱的外表面都喷上油漆,那么共需喷多少平方米的油漆
解:因为3a·2b·ab=6a2b2(m3),
所以这个包装箱的体积为6a2b2 m3.
解:包装箱的表面积为2(3a·2b+3a·ab+2b·ab)=(12ab+6a2b+4ab2)m2,
所以共需喷(12ab+6a2b+4ab2)m2的油漆.
例3 已知-2x3m+1y2n与7xy2的积与x5y8是同类项,求m2+n的值.
所以m2+n=12+3=1+3=4.
解:因为-2x3m+1y2n与7xy2的积与x5y8是同类项,
解:长方形的面积是xym2,
则绿化的面积是 x×y=xy(m2),
所以剩下的面积是xy-xy=xy(m2).
2.有一块长为xm,宽为ym的长方形空地,现在要在这块地中规划一块长xm,宽ym的长方形空地用于绿化,求绿化的面积和剩下的面积.
2.计算3a·(-2a)2的结果为 ( )
A.-12a3 B.-6a2 C.12a3 D.6a2
1.计算2a·ab的结果是 ( )
A.2ab B.2a2b C.3ab D.3a2b
B
C
B
3.小刘做了四道题目:①3x3y·2xyz2=5x4y2z2;②2a2·(-3a)3=-54a6;
③(-m2n)2·(-8mn2)=-2m5n4;④-3a3b·(-3ab)=9a4b2.他做对的题目是
( )
A.①② B.③④
C.①②③ D.②③④
5.若(-5am+1b2n-1)·2ab3=-10a4b4,则m-n的值为 ( )
A.-3 B.-1
C.1 D.3
4.一块长方形草坪的长是3xa+1 m,宽是2xb-1 m(a,b均为大于1的正整数),则长方形草坪的面积是 ( )
A.6xa-b m2 B.6xa+b m2
C.6xa+b-1 m2 D.6xa+b-2 m2
B
C
5.计算:
(1)4xy2z·(-0.5x2y)3; (2)3a2·(-ab)·(-2a2b)3;
(3)(-a4b)3·a-(2a4b)2·(-a5b).
解:(1)原式=4xy2z·(-x6y3)
=-x7y5z.
(2)原式=3a2·(-ab)·(-8a6b3)
=3a9b4.
(3)原式=(-a12b3)·a-4a8b2·(-a5b)
=-a13b3+3a13b3
=2a13b3.
解:5a·(2a+a)-2a(5a-3a)
=5a·3a-2a·2a
=15a2-4a2
=11a2.
故阴影部分的面积为11a2.
6.求图中阴影部分的面积.(列式写过程)
7.已知9an-6b-2-n与-2a3m+1b2n的积与5a4b是同类项,求(m-n)2024的值.
解:因为9an-6b-2-n与-2a3m+1b2n的积与5a4b是同类项,
所以-2-n+2n=1,n-6+3m+1=4,
解得n=3,m=2,
所以(m-n)2024=(2-3)2024=1.
单项式乘单项式法则
整式的
乘法
单项式与单项式相乘,把它们的系数、同底数幂分别相乘,其余字母连同它的指数不变,作为积的因式.
一系数相乘;
二相同字母的幂相乘;
三其余字母连同它的指数不变,作为积的因式.
步骤
同课章节目录
