2.2探索直线平行的条件 第1课时 利用同位角判定两直线平行 课件(共25张PPT)
文档属性
| 名称 | 2.2探索直线平行的条件 第1课时 利用同位角判定两直线平行 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-12 19:10:01 | ||
图片预览








文档简介
(共25张PPT)
2.2 探索直线平行的条件
第1课时 利用同位角判定两直线平行
1. 理解并掌握同位角的概念,能够运用同位角相等判定两直线平行;(重点)
2. 理解并掌握平行线基本事实,能够运用其解决实际问题.(难点)
简称“三线八角”.
两条直线相交,可以构成四个角,若在图中再添加一条直线,即直线EF被第三条直线CD所截,构成了几个角?
6
7
5
8
B
A
F
E
C
D
4
3
1
2
在日常生活中,人们经常用到平行线.如图,装修工人正在向墙上钉木条.如果木条b与墙壁边缘垂直, 那么木条a 与墙壁边缘所成的角为多少度时,才能使木条a与木条b平行?
你知道其中的理由吗?
如果木条b不与墙壁边缘垂直呢?
(1)如图,三根木条相交成∠1, ∠2,固定木条b,c,转动木条a.
如图,在木条a的转动过程中,观察∠2的变化以及它与∠1的大小关系,你发现木条a与木条b的位置关系发生了什么变化?木条a何时与木条b平行?
探究一:同位角的概念
当∠1>∠2时
当∠1=∠2时
当∠1<∠2时
①直线a和b不平行
②直线a和b平行
③直线a和b不平行
A
C
B
D
l
1
3
7
5
2
4
8
6
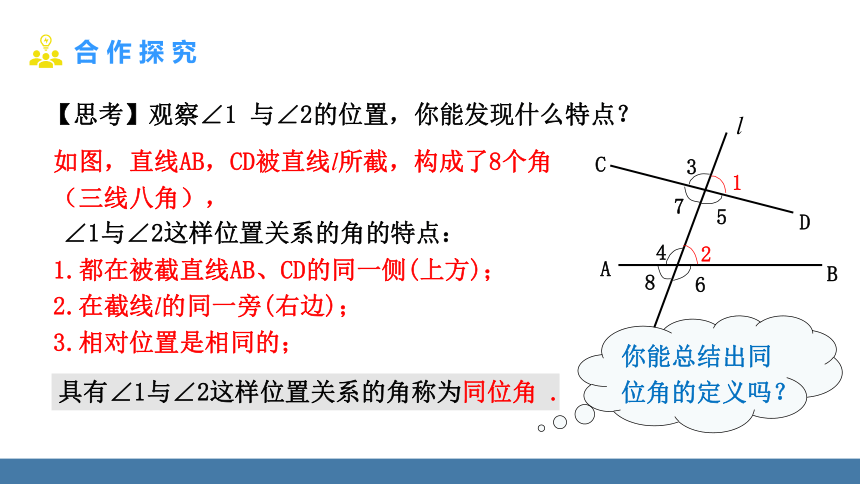
如图,直线AB,CD被直线l所截,构成了8个角(三线八角),
1.都在被截直线AB、CD的同一侧(上方);
2.在截线l的同一旁(右边);
3.相对位置是相同的;
具有∠1与∠2这样位置关系的角称为同位角 .
你能总结出同位角的定义吗?
【思考】观察∠1 与∠2的位置,你能发现什么特点?
∠1与∠2这样位置关系的角的特点:
两直线被第三条直线所截,位于两条直线(被截线)同一方、且在第三条直线(截线)同一侧的两个角,(位置相同的一对角)叫做同位角.
图中还有类似于∠1与∠2的同位角吗?
∠3与∠4;
∠5与∠6;
∠7与∠8.
A
C
B
D
l
1
3
7
5
2
4
8
6
同位角
图形特征:在形如字母“F”的图形中有同位角.
变式图形:图中的∠1与∠2都是同位角.
C
解析:选项A,B,D中,∠1与∠2在截线的同旁,并且在被截线的同侧,是同位角,即在图中可找到形如“F”的模型;选项C中,∠1与∠2没有公共边,不是同位角.故选C.
例1 下列图形中,∠1和∠2不是同位角的是 ( )
探究二:利用同位角判定两条直线平行
由上面的操作过程,你能发现判定两直线平行的方法吗?
1
2
l2
l1
A
B
∠1与∠2的大小满足什么关系时,木条a与木条b平行?
当∠1=∠2时,
直线a和b平行;
2
1
l2
l1
B
A
判定方法1:两条直线被第三条直线所截 ,如果同位角相等,
那么这两条直线平行.
简称为:同位角相等,两直线平行.
两直线平行,用符号“∥”表示.
例如,直线a与直线b平行,记作a∥b.
应用格式:
∵∠1=∠2(已知)
∴l1∥l2(同位角相等,两直线平行)
对顶角相等
∠3
等量代换
同位角相等,两直线平行
例2 如图所示,已知∠1=∠2,试说明AB与CD的位置关系.
解:AB∥CD.
理由:∵∠1=∠2(已知),
∠2=∠3( ),
∴∠1= ( ),
∴AB∥CD( ).
3
解:AB∥CD.
理由如下:
∵∠1+∠2=180°(已知),
∠2+∠3=180°(平角的定义),
∴∠1=∠3(同角的补角相等).
∴AB∥CD(同位角相等,两直线平行).
1.如图所示,已知直线AB,CD被直线EF所截,∠1+∠2=180°,AB与CD平行吗 请说明理由.
(1)你能借助三角尺画平行线吗?小明按如下方法画出了两条已知直线的平行线,请说明其中的道理.
探究三:平行线的画法及性质
一放
二靠
三推
四画
依据是: .
同位角相等,两直线平行
想一想:怎样用三角尺和直尺画平行线?
C
·
A
B
结论:过直线外一点有且只有一条直线与这条直线平行.
只能画一条
你能得到什么结论?
(唯一性)
(2)你能过直线AB外一点C画直线AB的平行线吗?能画出几条?
A
B
C
·
·
D
E
F
G
H
结论:平行于同一条直线的两条直线平行.
b
a
c
你能得到什么结论?
(传递性)
在图中,分别过点C和D画直线AB的平行线EF和GH,那么EF与GH有怎样的位置关系?
几何语言:∵b∥a,c∥a,
∴b∥c.
解析:根据平行线性质的推论得出答案即可.
解:由题意,得CD∥EF,EF∥AB,
所以CD∥AB.
例3 如图所示,将一张长方形的硬纸片ABCD对折后打开,折痕为EF.把长方形ABEF平摊在桌面上,另一面CDFE无论怎样改变位置,总有CD∥AB存在,为什么
解:(1)如图.
(2)AB∥CD.
理由:
∵AB∥EF,CD∥EF,
∴AB∥CD.
A B
C D
2.如图所示,P,Q是直线EF外两点.
(1)过点P画直线AB∥EF,过点Q画直线CD∥EF;
(2)AB与CD有怎样的位置关系 为什么
1.下列结论错误的是( )
A.同位角相等,两直线平行
B.过一点有且只有一条直线与已知直线平行
C.同一平面内,不相交的两条直线叫做平行线
D.如果两条直线都与第三条直线平行,那么这两条直线也平行
B
D
2.图中∠1与∠2是同位角的有 ( )
A.1个 B.2个 C.3个 D.4个
∠B=∠ECD
b∥c
12
3.如图所示,根据“同位角相等,两直线平行”,可判定AB∥CE的条件是 .
4.如图所示,直线a∥c,∠1=∠2,那么直线b,c的位置关系是 .
5.如图所示,∠A=70°,O是射线AB上一点,直线OD与AB所夹角∠BOD=82°,要使OD∥AC,则直线OD应绕点O按逆时针方向至少旋转 °.
解:EB∥FD.
理由:∵AB⊥MN,CD⊥MN(已知),
∴∠ABM=∠CDM=90°(垂直的定义).
∵∠1=∠2(已知),
∴∠ABM-∠1=∠CDM-∠2(等式的性质),即∠EBM=∠FDM.
∴EB∥FD(同位角相等,两直线平行).
6.如图所示,已知AB⊥MN,垂足为B,CD⊥MN,垂足为D, ∠1=∠2,那么EB与FD平行吗 请说明理由.
解:AB∥CD∥EF.理由如下:如图,
∵∠1=∠3,
∴AB∥EF(同位角相等,两直线平行).
又∵∠1+∠2=180°(已知),∠1+∠4=180°(平角的定义),
∴∠2=∠4(同角的补角相等).
∴AB∥CD(同位角相等,两直线平行),∴AB∥CD∥EF.
4
7.如图所示,∠1=∠3,∠1+∠2=180°,则AB,CD,EF的位置关系如何 请说明理由.
探索直线平行的条件
两直线平行判定方法1
同位角
平行线的性质
两直线被第三条直线所截,位于两条直线(被截线)同一方、且在第三直线(截线)同一侧的两个角,(位置相同的一对角)叫做同位角.
两条直线被第三条直线所截 ,如果同位角相等,那么这两条直线平行.
1.经过直线外一点,有且只有一条直线与这条直线平行.
2.平行于同一条直线的两条直线平行.
2.2 探索直线平行的条件
第1课时 利用同位角判定两直线平行
1. 理解并掌握同位角的概念,能够运用同位角相等判定两直线平行;(重点)
2. 理解并掌握平行线基本事实,能够运用其解决实际问题.(难点)
简称“三线八角”.
两条直线相交,可以构成四个角,若在图中再添加一条直线,即直线EF被第三条直线CD所截,构成了几个角?
6
7
5
8
B
A
F
E
C
D
4
3
1
2
在日常生活中,人们经常用到平行线.如图,装修工人正在向墙上钉木条.如果木条b与墙壁边缘垂直, 那么木条a 与墙壁边缘所成的角为多少度时,才能使木条a与木条b平行?
你知道其中的理由吗?
如果木条b不与墙壁边缘垂直呢?
(1)如图,三根木条相交成∠1, ∠2,固定木条b,c,转动木条a.
如图,在木条a的转动过程中,观察∠2的变化以及它与∠1的大小关系,你发现木条a与木条b的位置关系发生了什么变化?木条a何时与木条b平行?
探究一:同位角的概念
当∠1>∠2时
当∠1=∠2时
当∠1<∠2时
①直线a和b不平行
②直线a和b平行
③直线a和b不平行
A
C
B
D
l
1
3
7
5
2
4
8
6
如图,直线AB,CD被直线l所截,构成了8个角(三线八角),
1.都在被截直线AB、CD的同一侧(上方);
2.在截线l的同一旁(右边);
3.相对位置是相同的;
具有∠1与∠2这样位置关系的角称为同位角 .
你能总结出同位角的定义吗?
【思考】观察∠1 与∠2的位置,你能发现什么特点?
∠1与∠2这样位置关系的角的特点:
两直线被第三条直线所截,位于两条直线(被截线)同一方、且在第三条直线(截线)同一侧的两个角,(位置相同的一对角)叫做同位角.
图中还有类似于∠1与∠2的同位角吗?
∠3与∠4;
∠5与∠6;
∠7与∠8.
A
C
B
D
l
1
3
7
5
2
4
8
6
同位角
图形特征:在形如字母“F”的图形中有同位角.
变式图形:图中的∠1与∠2都是同位角.
C
解析:选项A,B,D中,∠1与∠2在截线的同旁,并且在被截线的同侧,是同位角,即在图中可找到形如“F”的模型;选项C中,∠1与∠2没有公共边,不是同位角.故选C.
例1 下列图形中,∠1和∠2不是同位角的是 ( )
探究二:利用同位角判定两条直线平行
由上面的操作过程,你能发现判定两直线平行的方法吗?
1
2
l2
l1
A
B
∠1与∠2的大小满足什么关系时,木条a与木条b平行?
当∠1=∠2时,
直线a和b平行;
2
1
l2
l1
B
A
判定方法1:两条直线被第三条直线所截 ,如果同位角相等,
那么这两条直线平行.
简称为:同位角相等,两直线平行.
两直线平行,用符号“∥”表示.
例如,直线a与直线b平行,记作a∥b.
应用格式:
∵∠1=∠2(已知)
∴l1∥l2(同位角相等,两直线平行)
对顶角相等
∠3
等量代换
同位角相等,两直线平行
例2 如图所示,已知∠1=∠2,试说明AB与CD的位置关系.
解:AB∥CD.
理由:∵∠1=∠2(已知),
∠2=∠3( ),
∴∠1= ( ),
∴AB∥CD( ).
3
解:AB∥CD.
理由如下:
∵∠1+∠2=180°(已知),
∠2+∠3=180°(平角的定义),
∴∠1=∠3(同角的补角相等).
∴AB∥CD(同位角相等,两直线平行).
1.如图所示,已知直线AB,CD被直线EF所截,∠1+∠2=180°,AB与CD平行吗 请说明理由.
(1)你能借助三角尺画平行线吗?小明按如下方法画出了两条已知直线的平行线,请说明其中的道理.
探究三:平行线的画法及性质
一放
二靠
三推
四画
依据是: .
同位角相等,两直线平行
想一想:怎样用三角尺和直尺画平行线?
C
·
A
B
结论:过直线外一点有且只有一条直线与这条直线平行.
只能画一条
你能得到什么结论?
(唯一性)
(2)你能过直线AB外一点C画直线AB的平行线吗?能画出几条?
A
B
C
·
·
D
E
F
G
H
结论:平行于同一条直线的两条直线平行.
b
a
c
你能得到什么结论?
(传递性)
在图中,分别过点C和D画直线AB的平行线EF和GH,那么EF与GH有怎样的位置关系?
几何语言:∵b∥a,c∥a,
∴b∥c.
解析:根据平行线性质的推论得出答案即可.
解:由题意,得CD∥EF,EF∥AB,
所以CD∥AB.
例3 如图所示,将一张长方形的硬纸片ABCD对折后打开,折痕为EF.把长方形ABEF平摊在桌面上,另一面CDFE无论怎样改变位置,总有CD∥AB存在,为什么
解:(1)如图.
(2)AB∥CD.
理由:
∵AB∥EF,CD∥EF,
∴AB∥CD.
A B
C D
2.如图所示,P,Q是直线EF外两点.
(1)过点P画直线AB∥EF,过点Q画直线CD∥EF;
(2)AB与CD有怎样的位置关系 为什么
1.下列结论错误的是( )
A.同位角相等,两直线平行
B.过一点有且只有一条直线与已知直线平行
C.同一平面内,不相交的两条直线叫做平行线
D.如果两条直线都与第三条直线平行,那么这两条直线也平行
B
D
2.图中∠1与∠2是同位角的有 ( )
A.1个 B.2个 C.3个 D.4个
∠B=∠ECD
b∥c
12
3.如图所示,根据“同位角相等,两直线平行”,可判定AB∥CE的条件是 .
4.如图所示,直线a∥c,∠1=∠2,那么直线b,c的位置关系是 .
5.如图所示,∠A=70°,O是射线AB上一点,直线OD与AB所夹角∠BOD=82°,要使OD∥AC,则直线OD应绕点O按逆时针方向至少旋转 °.
解:EB∥FD.
理由:∵AB⊥MN,CD⊥MN(已知),
∴∠ABM=∠CDM=90°(垂直的定义).
∵∠1=∠2(已知),
∴∠ABM-∠1=∠CDM-∠2(等式的性质),即∠EBM=∠FDM.
∴EB∥FD(同位角相等,两直线平行).
6.如图所示,已知AB⊥MN,垂足为B,CD⊥MN,垂足为D, ∠1=∠2,那么EB与FD平行吗 请说明理由.
解:AB∥CD∥EF.理由如下:如图,
∵∠1=∠3,
∴AB∥EF(同位角相等,两直线平行).
又∵∠1+∠2=180°(已知),∠1+∠4=180°(平角的定义),
∴∠2=∠4(同角的补角相等).
∴AB∥CD(同位角相等,两直线平行),∴AB∥CD∥EF.
4
7.如图所示,∠1=∠3,∠1+∠2=180°,则AB,CD,EF的位置关系如何 请说明理由.
探索直线平行的条件
两直线平行判定方法1
同位角
平行线的性质
两直线被第三条直线所截,位于两条直线(被截线)同一方、且在第三直线(截线)同一侧的两个角,(位置相同的一对角)叫做同位角.
两条直线被第三条直线所截 ,如果同位角相等,那么这两条直线平行.
1.经过直线外一点,有且只有一条直线与这条直线平行.
2.平行于同一条直线的两条直线平行.
同课章节目录
