3.2频率的稳定性 第2课时 用频率估计概率 课件(共20张PPT)
文档属性
| 名称 | 3.2频率的稳定性 第2课时 用频率估计概率 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-12 19:15:02 | ||
图片预览







文档简介
(共20张PPT)
3.2 频率的稳定性
第2课时 用频率估计概率
1.学会根据问题的特点,用统计来估计事件发生的概率,培养分析问题,解决问题的能力;(重点)
2.通过对问题的分析,理解并掌握用频率来估计概率的方法,渗透转化和估算的思想方法.(难点)
抛掷一枚均匀的硬币,硬币落下后,会出现两种情况:
正面朝上
正面朝下
你认为正面朝上和正面朝下的可能性相同吗
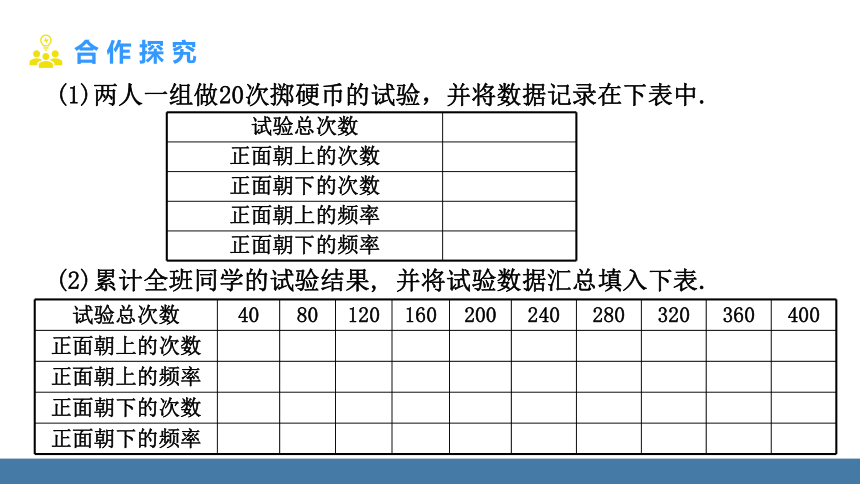
(1)两人一组做20次掷硬币的试验,并将数据记录在下表中.
试验总次数
正面朝上的次数
正面朝下的次数
正面朝上的频率
正面朝下的频率
(2)累计全班同学的试验结果, 并将试验数据汇总填入下表.
试验总次数 40 80 120 160 200 240 280 320 360 400
正面朝上的次数
正面朝上的频率
正面朝下的次数
正面朝下的频率
(3)根据表格,完成下面的折线统计图.
40
80
120
160
200
240
280
320
360
400
0.2
0.4
0.6
0.8
1.0
频率
试验总次数
0.5
0
当试验次数很多时, 正面朝上的频率折线差不多稳定在“ 0.5 水平直线”上.
(4)观察上面的折线统计图,你发现了什么规律?
当实验的次数较少时,折线在“0.5水平直线”的上下摆动的幅度较大,随着实验的次数的增加,折线在“0.5水平直线”的上下摆动的幅度会逐渐变小.
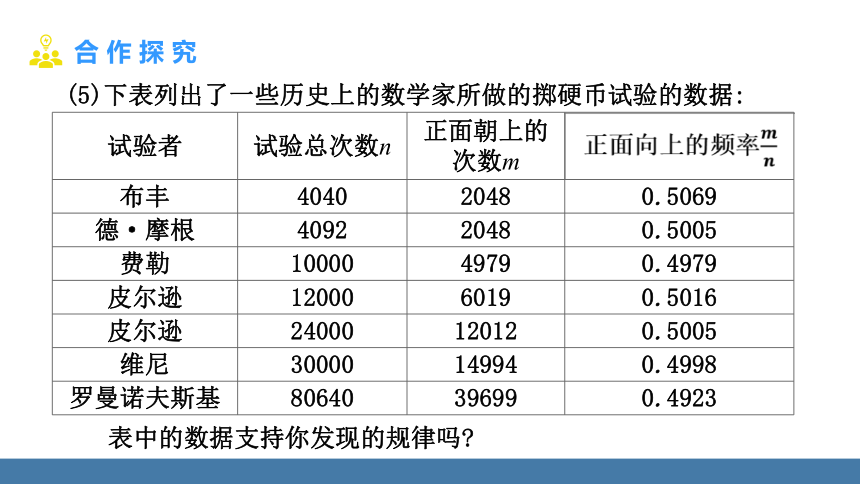
(5)下表列出了一些历史上的数学家所做的掷硬币试验的数据:
试验者 试验总次数n 正面朝上的 次数m 正面向上的频率
布丰 4040 2048 0.5069
德·摩根 4092 2048 0.5005
费勒 10000 4979 0.4979
皮尔逊 12000 6019 0.5016
皮尔逊 24000 12012 0.5005
维尼 30000 14994 0.4998
罗曼诺夫斯基 80640 39699 0.4923
表中的数据支持你发现的规律吗
无论是掷质地均匀的硬币还是抛瓶盖,在试验次数很大时,正面朝上(盖口向上)的频率都会在一个常数附近摆动,这就是频率的稳定性.
我们把刻画事件A发生的可能性大小的数值,称为事件A发生的概率,记为P(A).
一般的,大量重复的试验中,我们常用随机事件A发生的频率来估计事件A发生的概率.
例1 一枚木质中国象棋子“兵”,它的正面雕刻一个“兵”字,它的反面是平滑的,将它从一定高度下掷,落地反弹后可能是“兵”字面朝上,也可能是“兵”字面朝下.由于棋子的两面不均匀,为了估计“兵”字面朝上的概率,某试验小组做了棋子下掷的试验,试验数据如下表:
试验次数 20 40 60 80 100 120 140 160
“兵”字面 朝上的次数 14 38 47 52 66 78 88
“兵”字面 朝上的频率 0.70 0.45 0.63 0.59 0.55 0.56
(1)请将上表补充完整;
18
0.52
0.55
(2)如图所示.
(3)估计下掷棋子一次,“兵”字面朝上的概率是多少.(结果保留小数点后两位)
(3)随着试验次数的增加,“兵”字面朝上的频率稳定在0.55附近,所以估计“兵”字面朝上的概率是0.55.
(2)在下图中画出“兵”字面朝上频率的折线统计图.
1.口袋中有9个球,其中有4个红球球,3个蓝球,2个白球,在下列事件中,发生的可能性为1的是( )
A.从口袋中拿一个球恰为红球
B.从口袋中拿出2个球都是白球
C.拿出6个球中至少有一个球是红球
D.从口袋中拿出的球恰为3红2白
C
随机事件A 发生的概率P(A)的取值范围是什么?必然事件发生的概率是多少?不可能事件发生的概率又是多少
必然事件发生的概率为1,不可能事件发生的概率为0,随机事件A发生的概率P(A)是0与1之间的一个常数.
(1)小明做了4次抛瓶盖的试验,其中有3次盖口向上,由此,他估计盖口向上的概率为 ,你同意他的想法吗 与同伴进行交流.
解:不同意.
一般地,在大量重复的试验中,一个随机事件发生的频率会在某一个常数附近摆动,我们才能称之为该事件发生的概率.小明只做了4次试验,试验的次数太少,只有当试验次数足够大时,才能用频率估计概率.
(2)掷一枚质地均匀的硬币,正面朝上的概率为 ,那么,掷 10 次硬币一定会有5次正面朝上吗 如何理解正面朝上的概率为 与同伴进行交流.
解:掷10次硬币不一定会有5次正面朝上.
概率值只是反映了事件发生的机会的大小,不是一定会发生.所以抛一枚质地均匀的硬币,正面朝上的概率为 但是,抛10次硬币,必有5次正面朝上是可能事件,不一定会发生.
频率
事件发生的频繁程度
在实际问题中,若事件的概率未知,常用频率作为它的估计值.
频率是试验时的统计值,是变化的,概率是理论值,是不变的,频率是概率的一个近似值.
稳定性
大量重复试验
回顾你做过的抛瓶盖和掷硬币试验,你对事件发生的频率和概率的关系有怎样的理解?
联系:
区别:
事件发生的
可能性大小
概率
1.下列说法中错误的是 ( )
A.必然事件发生的概率为1
B.不可能事件发生的概率为0
C.概率很小的事件不可能发生
D.随机事件发生的概率大于0且小于1
C
C
2.若从一个袋子里摸到红球的概率为1%,则下列说法中正确的是( )
A.摸1次一定不会摸到红球
B.摸100次一定能摸到红球
C.摸1次有可能摸到红球
D.摸100次一定能摸到1次红球
D
3.在利用正六面体骰子进行频率估计概率的试验中,小闽同学统计了某一结果朝上的频率,绘出的统计图如图所示,则符合这一结果的试验可能是( )
A.朝上的点数是6的概率
B.朝上的点数是偶数的概率
C.朝上的点数小于4的概率
D.朝上的点数是3的整数倍的概率
4.某射击运动员在同一条件下的射击成绩记录如下:根据频率的稳定性,估计这名运动员射击一次时“射中9环以上”的概率是 (结果保留小数点后一位).
射击次数 20 40 100 200 400 1000
“射中9环以上”的次数 15 33 78 158 321 801
“射中9环以上”的频率(结果保留小数点后两位) 0.75 0.83 0.78 0.79 0.80 0.80
0.8
0.9
5400
5.某市林业局要移植一种树苗,对附近地区去年这种树苗移植成活的情况进行调查统计,并绘制了折线统计图(如图所示).
(1)这种树苗成活概率的估计值为 ;
(2)若移植这种树苗6000棵,估计可以成活 棵;
(3)若计划成活9000棵这种树苗,则需移植这种树苗大约多少棵
解:(3)9000÷0.9=10000(棵).
故需移植这种树苗大约10000棵.
频率估计概率
我们把刻画事件A发生的可能性大小的数值,称为事件A发生的概率,记为P(A).
一般的,大量重复的试验中,我们常用随机事件A发生的频率来估计事件A发生的概率.
必然事件发生的概率为1;不可能事件发生的概率为0;随机事件A发生的概率P(A)是0与1之间的一个常数.
3.2 频率的稳定性
第2课时 用频率估计概率
1.学会根据问题的特点,用统计来估计事件发生的概率,培养分析问题,解决问题的能力;(重点)
2.通过对问题的分析,理解并掌握用频率来估计概率的方法,渗透转化和估算的思想方法.(难点)
抛掷一枚均匀的硬币,硬币落下后,会出现两种情况:
正面朝上
正面朝下
你认为正面朝上和正面朝下的可能性相同吗
(1)两人一组做20次掷硬币的试验,并将数据记录在下表中.
试验总次数
正面朝上的次数
正面朝下的次数
正面朝上的频率
正面朝下的频率
(2)累计全班同学的试验结果, 并将试验数据汇总填入下表.
试验总次数 40 80 120 160 200 240 280 320 360 400
正面朝上的次数
正面朝上的频率
正面朝下的次数
正面朝下的频率
(3)根据表格,完成下面的折线统计图.
40
80
120
160
200
240
280
320
360
400
0.2
0.4
0.6
0.8
1.0
频率
试验总次数
0.5
0
当试验次数很多时, 正面朝上的频率折线差不多稳定在“ 0.5 水平直线”上.
(4)观察上面的折线统计图,你发现了什么规律?
当实验的次数较少时,折线在“0.5水平直线”的上下摆动的幅度较大,随着实验的次数的增加,折线在“0.5水平直线”的上下摆动的幅度会逐渐变小.
(5)下表列出了一些历史上的数学家所做的掷硬币试验的数据:
试验者 试验总次数n 正面朝上的 次数m 正面向上的频率
布丰 4040 2048 0.5069
德·摩根 4092 2048 0.5005
费勒 10000 4979 0.4979
皮尔逊 12000 6019 0.5016
皮尔逊 24000 12012 0.5005
维尼 30000 14994 0.4998
罗曼诺夫斯基 80640 39699 0.4923
表中的数据支持你发现的规律吗
无论是掷质地均匀的硬币还是抛瓶盖,在试验次数很大时,正面朝上(盖口向上)的频率都会在一个常数附近摆动,这就是频率的稳定性.
我们把刻画事件A发生的可能性大小的数值,称为事件A发生的概率,记为P(A).
一般的,大量重复的试验中,我们常用随机事件A发生的频率来估计事件A发生的概率.
例1 一枚木质中国象棋子“兵”,它的正面雕刻一个“兵”字,它的反面是平滑的,将它从一定高度下掷,落地反弹后可能是“兵”字面朝上,也可能是“兵”字面朝下.由于棋子的两面不均匀,为了估计“兵”字面朝上的概率,某试验小组做了棋子下掷的试验,试验数据如下表:
试验次数 20 40 60 80 100 120 140 160
“兵”字面 朝上的次数 14 38 47 52 66 78 88
“兵”字面 朝上的频率 0.70 0.45 0.63 0.59 0.55 0.56
(1)请将上表补充完整;
18
0.52
0.55
(2)如图所示.
(3)估计下掷棋子一次,“兵”字面朝上的概率是多少.(结果保留小数点后两位)
(3)随着试验次数的增加,“兵”字面朝上的频率稳定在0.55附近,所以估计“兵”字面朝上的概率是0.55.
(2)在下图中画出“兵”字面朝上频率的折线统计图.
1.口袋中有9个球,其中有4个红球球,3个蓝球,2个白球,在下列事件中,发生的可能性为1的是( )
A.从口袋中拿一个球恰为红球
B.从口袋中拿出2个球都是白球
C.拿出6个球中至少有一个球是红球
D.从口袋中拿出的球恰为3红2白
C
随机事件A 发生的概率P(A)的取值范围是什么?必然事件发生的概率是多少?不可能事件发生的概率又是多少
必然事件发生的概率为1,不可能事件发生的概率为0,随机事件A发生的概率P(A)是0与1之间的一个常数.
(1)小明做了4次抛瓶盖的试验,其中有3次盖口向上,由此,他估计盖口向上的概率为 ,你同意他的想法吗 与同伴进行交流.
解:不同意.
一般地,在大量重复的试验中,一个随机事件发生的频率会在某一个常数附近摆动,我们才能称之为该事件发生的概率.小明只做了4次试验,试验的次数太少,只有当试验次数足够大时,才能用频率估计概率.
(2)掷一枚质地均匀的硬币,正面朝上的概率为 ,那么,掷 10 次硬币一定会有5次正面朝上吗 如何理解正面朝上的概率为 与同伴进行交流.
解:掷10次硬币不一定会有5次正面朝上.
概率值只是反映了事件发生的机会的大小,不是一定会发生.所以抛一枚质地均匀的硬币,正面朝上的概率为 但是,抛10次硬币,必有5次正面朝上是可能事件,不一定会发生.
频率
事件发生的频繁程度
在实际问题中,若事件的概率未知,常用频率作为它的估计值.
频率是试验时的统计值,是变化的,概率是理论值,是不变的,频率是概率的一个近似值.
稳定性
大量重复试验
回顾你做过的抛瓶盖和掷硬币试验,你对事件发生的频率和概率的关系有怎样的理解?
联系:
区别:
事件发生的
可能性大小
概率
1.下列说法中错误的是 ( )
A.必然事件发生的概率为1
B.不可能事件发生的概率为0
C.概率很小的事件不可能发生
D.随机事件发生的概率大于0且小于1
C
C
2.若从一个袋子里摸到红球的概率为1%,则下列说法中正确的是( )
A.摸1次一定不会摸到红球
B.摸100次一定能摸到红球
C.摸1次有可能摸到红球
D.摸100次一定能摸到1次红球
D
3.在利用正六面体骰子进行频率估计概率的试验中,小闽同学统计了某一结果朝上的频率,绘出的统计图如图所示,则符合这一结果的试验可能是( )
A.朝上的点数是6的概率
B.朝上的点数是偶数的概率
C.朝上的点数小于4的概率
D.朝上的点数是3的整数倍的概率
4.某射击运动员在同一条件下的射击成绩记录如下:根据频率的稳定性,估计这名运动员射击一次时“射中9环以上”的概率是 (结果保留小数点后一位).
射击次数 20 40 100 200 400 1000
“射中9环以上”的次数 15 33 78 158 321 801
“射中9环以上”的频率(结果保留小数点后两位) 0.75 0.83 0.78 0.79 0.80 0.80
0.8
0.9
5400
5.某市林业局要移植一种树苗,对附近地区去年这种树苗移植成活的情况进行调查统计,并绘制了折线统计图(如图所示).
(1)这种树苗成活概率的估计值为 ;
(2)若移植这种树苗6000棵,估计可以成活 棵;
(3)若计划成活9000棵这种树苗,则需移植这种树苗大约多少棵
解:(3)9000÷0.9=10000(棵).
故需移植这种树苗大约10000棵.
频率估计概率
我们把刻画事件A发生的可能性大小的数值,称为事件A发生的概率,记为P(A).
一般的,大量重复的试验中,我们常用随机事件A发生的频率来估计事件A发生的概率.
必然事件发生的概率为1;不可能事件发生的概率为0;随机事件A发生的概率P(A)是0与1之间的一个常数.
同课章节目录
