4.1认识三角形 第2课时 三角形的三边关系 课件(共18张PPT)
文档属性
| 名称 | 4.1认识三角形 第2课时 三角形的三边关系 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-13 06:57:18 | ||
图片预览





文档简介
(共18张PPT)
4.1 认识三角形
第2课时 三角形的三边关系
1. 掌握三角形按边分类的方法,能够判定三角形是否为特殊三角形;(重点)
2. 探索并掌握三角形三边之间的关系,运用三角形三边关系解决有关问题.(难点)
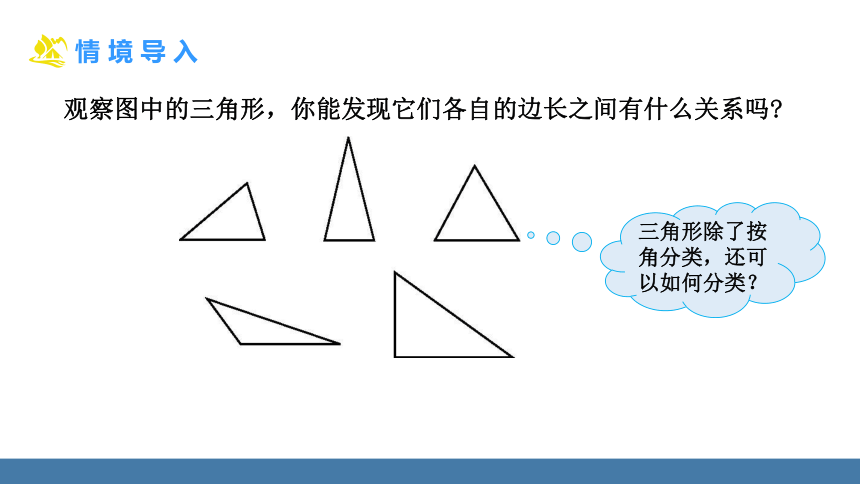
三角形除了按角分类,还可以如何分类?
观察图中的三角形,你能发现它们各自的边长之间有什么关系吗
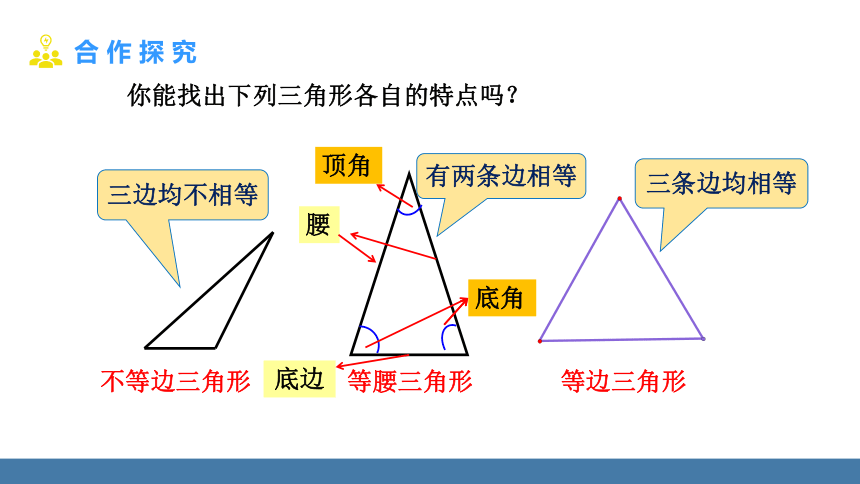
不等边三角形
等腰三角形
等边三角形
三边均不相等
有两条边相等
三条边均相等
腰
底边
顶角
底角
你能找出下列三角形各自的特点吗?
有两条边相等的三角形叫作等腰三角形;
三条边都相等的三角形叫作等边三角形.
按边分类
等腰三角形
三边都不相等的三角形
有两条边相等的三角形(其中三边都相等的叫等边三角形)
例1 用一根长为18厘米的细铁丝围成一个等腰三角形.如果腰长是底边长的2倍,那么三边的长分别是多少
解:设底边长为 x 厘米,则腰长为 2x 厘米.
由题意,得 x+2x+2x=18,
解得 x=3.6.
所以三边的长分别为3.6厘米,7.2厘米,7.2厘米.
1.如果等腰三角形的底边长是5cm,腰长是8cm,则这个等腰三角形的周长为______________.
21cm
解:装有黄色彩灯的电线长.
可以得出:
(1)节日的晚上,房间内亮起了彩灯.如图,装有黄色彩灯的电线与装有红色彩灯的电线哪根长呢?说明你的理由.
方法一:测量
方法二:根据“两点之间的所有连线中,线段最短”的结论,
也可以得出: .
B C
A
a
b
c
B
A
C
如图,根据“两点之间线段最短”,
可得a+b>c.
同理b+c>a,a+c>b.
你能得出什么样的结论?
(2)在一个三角形中,任意两边之和与第三边的长度有怎样的关系 为什么
三角形的任意两边之和大于第三边.
计算每个三角形的任意两边之差,并与第三边比较,你能得到什么结论 再画一些三角形试一试.
1.分别量出图中三个三角形的三边长度,并填入空格内.
(1)a= ,b= ,c= ;
(2)a= ,b= ,c= ;
(3)a= ,b= ,c= .
2.如图 ,在△ABC中,以点B为圆心,以BA的长为半径作弧,与边 BC交于点D,图中是否有线段长度等于BC-AB呢 能用圆规直观说明 BC-AB与AC之间的大小关系吗 改变三角形的形状再试试看,你能得到什么结论
解:①图中线段CD等于BC-AB.
②由于BC-AB=CD,且线段CD与线段AC相交于点C,所以可以用圆规以点C为圆心画弧且交于线段AC于一点,那么BC-AB的长度小于线段AC的长度.
③无论三角形是什么形状,三角形的两边之差始终小于第三边.
因此,我们可以得出三角形的三边关系为:
三角形任意两边之和 .
三角形任意两边之差 .
大于第三边
小于第三边
a
b
c
B
A
C
三条线段能够组成三角形的条件.
两边之差<第三边<两边之和
AB-AC< BC <AB+AC
例2 有两根长度分别为5cm和8cm的木棒,用长度为2cm的木棒与它们能摆成三角形吗?为什么?长度为13cm的木棒呢?
解:取长度为2cm的木棒时,由于2+5=7<8,出现了两边之和小于第三边的情况,所以它们不能摆成三角形.
用长度为13cm的木棒时,由于5+8=13,出现了两边之和等于第三边的情况,所以它们也不能摆成三角形.
如果一根木棒能与原来的两根木棒摆成三角形,那么它的长度取值范围是什么?
归纳 判断三角形边的取值范围要同时运用两边之和大于第三边,两边之差小于第三边.
2.判断下列长度的三条线段能否拼成三角形?为什么?
(1)3cm,8cm,4cm;
(2)5cm,6cm,11cm;
(3)5cm,6cm,10cm.
解:(1)不能,因为3cm+4cm<8cm;
(2)不能,因为5cm+6cm=11cm;
(3)能,因为5cm+6cm>10cm.
1.下列长度的三条线段,能组成三角形的是( )
A.3,4,8 B.5,6,10 C.5,5,11 D.5,6,11
B
D
3.已知AB=3,BC=1,则AC的长度的取值范围是( )
A.2≤AC≤4 B.2C.1≤AC≤3 D.1B
2.如图所示,为估计池塘岸边A,B间的距离,小方在池塘的一侧选取一点O,测得OA=15米,OB=10米,则A,B间的距离不可能是 ( )
A.20米 B.15米 C.10米 D.5米
4. 一个三角形的两边长分别是2和6,第三边长为偶数,则第三边长为 .
6
5.已知等腰三角形的一边长等于7,另一边长等于8,则它的周长为 .
6.a,b,c分别为△ABC的三边长,化简|a+b+c|-|c-a-b|的结果
为 .
22或23
2c
7.小颖要制作一个三角形木架,现有两根长度为8cm和5cm的木棒,如果要求第三根木棒的长度是偶数,小颖有几种选法?第三根的长度可以是多少?
∵x为偶数,
∴小颖有5种选法.
第三根木棒的长度可以是4cm,6cm,8cm,10cm,12cm.
解:设第三根木棒长为xcm,有8-5<x<8+5,
即3<x<13.
内容
三角形任意两边之和大于第三边.
三角形任意两边之差小于第三边.
三角形的
三边关系
三边关系
三角形按边分类
不等边三角形
等腰三角形(包括等边三角形)
依据
两点之间线段最短.
应用
判断三条线段能否构成三角形.
4.1 认识三角形
第2课时 三角形的三边关系
1. 掌握三角形按边分类的方法,能够判定三角形是否为特殊三角形;(重点)
2. 探索并掌握三角形三边之间的关系,运用三角形三边关系解决有关问题.(难点)
三角形除了按角分类,还可以如何分类?
观察图中的三角形,你能发现它们各自的边长之间有什么关系吗
不等边三角形
等腰三角形
等边三角形
三边均不相等
有两条边相等
三条边均相等
腰
底边
顶角
底角
你能找出下列三角形各自的特点吗?
有两条边相等的三角形叫作等腰三角形;
三条边都相等的三角形叫作等边三角形.
按边分类
等腰三角形
三边都不相等的三角形
有两条边相等的三角形(其中三边都相等的叫等边三角形)
例1 用一根长为18厘米的细铁丝围成一个等腰三角形.如果腰长是底边长的2倍,那么三边的长分别是多少
解:设底边长为 x 厘米,则腰长为 2x 厘米.
由题意,得 x+2x+2x=18,
解得 x=3.6.
所以三边的长分别为3.6厘米,7.2厘米,7.2厘米.
1.如果等腰三角形的底边长是5cm,腰长是8cm,则这个等腰三角形的周长为______________.
21cm
解:装有黄色彩灯的电线长.
可以得出:
(1)节日的晚上,房间内亮起了彩灯.如图,装有黄色彩灯的电线与装有红色彩灯的电线哪根长呢?说明你的理由.
方法一:测量
方法二:根据“两点之间的所有连线中,线段最短”的结论,
也可以得出: .
B C
A
a
b
c
B
A
C
如图,根据“两点之间线段最短”,
可得a+b>c.
同理b+c>a,a+c>b.
你能得出什么样的结论?
(2)在一个三角形中,任意两边之和与第三边的长度有怎样的关系 为什么
三角形的任意两边之和大于第三边.
计算每个三角形的任意两边之差,并与第三边比较,你能得到什么结论 再画一些三角形试一试.
1.分别量出图中三个三角形的三边长度,并填入空格内.
(1)a= ,b= ,c= ;
(2)a= ,b= ,c= ;
(3)a= ,b= ,c= .
2.如图 ,在△ABC中,以点B为圆心,以BA的长为半径作弧,与边 BC交于点D,图中是否有线段长度等于BC-AB呢 能用圆规直观说明 BC-AB与AC之间的大小关系吗 改变三角形的形状再试试看,你能得到什么结论
解:①图中线段CD等于BC-AB.
②由于BC-AB=CD,且线段CD与线段AC相交于点C,所以可以用圆规以点C为圆心画弧且交于线段AC于一点,那么BC-AB的长度小于线段AC的长度.
③无论三角形是什么形状,三角形的两边之差始终小于第三边.
因此,我们可以得出三角形的三边关系为:
三角形任意两边之和 .
三角形任意两边之差 .
大于第三边
小于第三边
a
b
c
B
A
C
三条线段能够组成三角形的条件.
两边之差<第三边<两边之和
AB-AC< BC <AB+AC
例2 有两根长度分别为5cm和8cm的木棒,用长度为2cm的木棒与它们能摆成三角形吗?为什么?长度为13cm的木棒呢?
解:取长度为2cm的木棒时,由于2+5=7<8,出现了两边之和小于第三边的情况,所以它们不能摆成三角形.
用长度为13cm的木棒时,由于5+8=13,出现了两边之和等于第三边的情况,所以它们也不能摆成三角形.
如果一根木棒能与原来的两根木棒摆成三角形,那么它的长度取值范围是什么?
归纳 判断三角形边的取值范围要同时运用两边之和大于第三边,两边之差小于第三边.
2.判断下列长度的三条线段能否拼成三角形?为什么?
(1)3cm,8cm,4cm;
(2)5cm,6cm,11cm;
(3)5cm,6cm,10cm.
解:(1)不能,因为3cm+4cm<8cm;
(2)不能,因为5cm+6cm=11cm;
(3)能,因为5cm+6cm>10cm.
1.下列长度的三条线段,能组成三角形的是( )
A.3,4,8 B.5,6,10 C.5,5,11 D.5,6,11
B
D
3.已知AB=3,BC=1,则AC的长度的取值范围是( )
A.2≤AC≤4 B.2
2.如图所示,为估计池塘岸边A,B间的距离,小方在池塘的一侧选取一点O,测得OA=15米,OB=10米,则A,B间的距离不可能是 ( )
A.20米 B.15米 C.10米 D.5米
4. 一个三角形的两边长分别是2和6,第三边长为偶数,则第三边长为 .
6
5.已知等腰三角形的一边长等于7,另一边长等于8,则它的周长为 .
6.a,b,c分别为△ABC的三边长,化简|a+b+c|-|c-a-b|的结果
为 .
22或23
2c
7.小颖要制作一个三角形木架,现有两根长度为8cm和5cm的木棒,如果要求第三根木棒的长度是偶数,小颖有几种选法?第三根的长度可以是多少?
∵x为偶数,
∴小颖有5种选法.
第三根木棒的长度可以是4cm,6cm,8cm,10cm,12cm.
解:设第三根木棒长为xcm,有8-5<x<8+5,
即3<x<13.
内容
三角形任意两边之和大于第三边.
三角形任意两边之差小于第三边.
三角形的
三边关系
三边关系
三角形按边分类
不等边三角形
等腰三角形(包括等边三角形)
依据
两点之间线段最短.
应用
判断三条线段能否构成三角形.
同课章节目录
