4.2全等三角形 课件(共18张PPT)
文档属性
| 名称 | 4.2全等三角形 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-13 06:55:23 | ||
图片预览




文档简介
(共18张PPT)
4.2 全等三角形
1. 理解全等三角形的概念,能识别全等三角形中的对应边、对应角;(重点)
2.掌握全等三角形的性质,能利用全等三角形的性质解决相关问题.(难点)
(1)
(2)
(3)
(4)
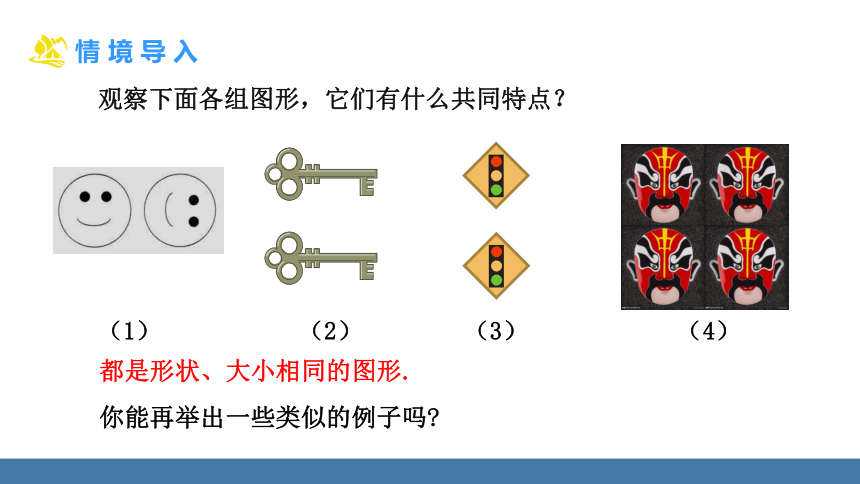
都是形状、大小相同的图形.
你能再举出一些类似的例子吗
观察下面各组图形,它们有什么共同特点?
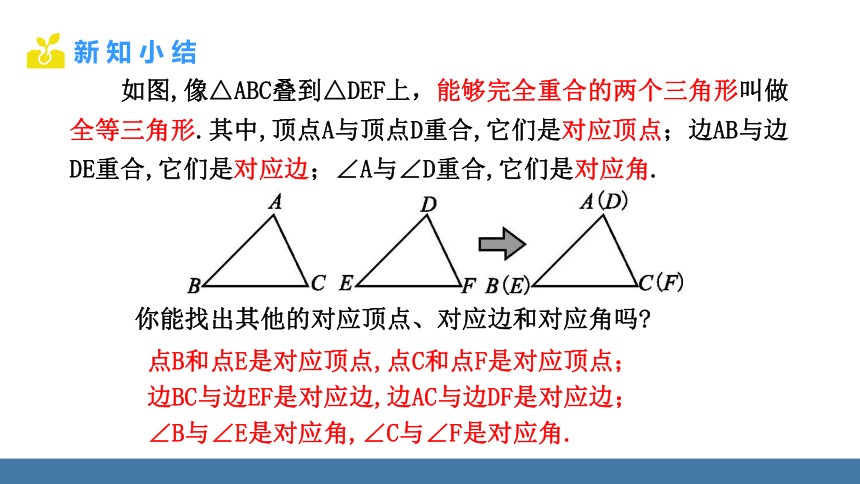
你能找出其他的对应顶点、对应边和对应角吗
点B和点E是对应顶点,点C和点F是对应顶点;
边BC与边EF是对应边,边AC与边DF是对应边;
∠B与∠E是对应角,∠C与∠F是对应角.
如图,像△ABC叠到△DEF上,能够完全重合的两个三角形叫做全等三角形.其中,顶点A与顶点D重合,它们是对应顶点;边AB与边DE重合,它们是对应边;∠A与∠D重合,它们是对应角.
A
B
C
F
E
D
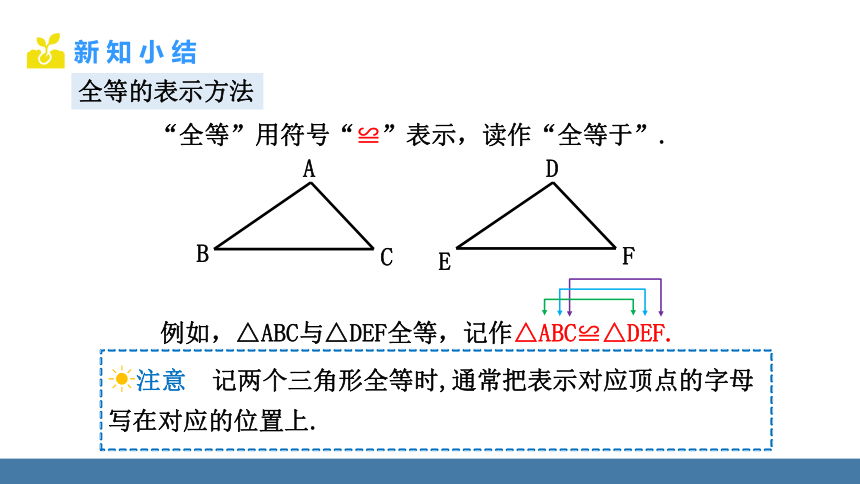
全等的表示方法
“全等”用符号“≌”表示,读作“全等于”.
注意 记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
例如,△ABC与△DEF全等,记作△ABC≌△DEF.
解:对应边:AB和AC,AD和AE,BD和CE;
对应角:∠A和∠A,∠B和∠C,∠ADB和∠AEC.
例1 如图所示,△ABD≌△ACE,AB=AC,写出它们的对应边和对应角.
解:△BOD与△COE的对应边为:BO与CO,OD与OE,BD与CE;
△ADO与△AEO的对应角为:∠DAO与∠EAO,∠ADO与∠AEO,
∠AOD与∠AOE.
1.如图,若△BOD≌△COE,∠B=∠C,指出这两个全等三角形的对应边;若△ADO≌△AEO,指出这两个三角形的对应角.
(1)每人准备两个全等三角形纸片,并画出两个三角形纸片对应边的高.全等三角形对应边的高相等吗 对应边的中线呢 对应的角平分线呢
(1)全等三角形对应边的高、中线以及对应的角平分线都相等.因此,全等三角形的对应线段都相等.
(2)如图,已知△ABC≌△A′B′C′,点D,E分别在BC边、AB边上请在△A′B′C′中画出与线段DE相对应的线段.图中有哪些相等的线段、相等的角?与同伴进行交流.
(2)在边B′C′上作线段B′D′=BD,在边B′A′上作线段B′E′=BE,连接E′D′.
E′
D′
(1)全等三角形的对应边 ,对应角 .
(2)全等三角形的对应线段(对应边的高,对应边的中线,对应角的平分线)都 .
相等
相等
相等
全等三角形的性质:
解:∵△ABC≌△DEF,∠A=32°,∠B=48°.
∴∠D=∠A=32°,∠E=∠B=48°.
在△DEF中,∠D+∠E+∠DFE=180°,
∴∠DFE=100°.
∵△ABC≌△DEF,
∴BC=EF,即BF+FC=EC+FC,
∴BF=EC.
∵BF=3,
∴EC=3.
例2 如图所示,已知△ABC≌△DEF,点E,C,F,B在同一直线上,∠A=32°,∠B=48°,BF=3,求∠DFE的度数和EC的长.
C
2.如图,△ABC≌△CDA,并且BC=DA,那么下列结论错误的是( )
A.∠1=∠2
B.∠ACB=∠DAC
C.AB=AD
D.∠B=∠D
如图所示.
准备一张等边三角形纸片,你能用折纸的办法把它分成两个全等三角形吗 能把它分成三个全等三角形吗 能把它分成四个全等三角形吗 与同伴进行交流。
D
B
D
4
1.如图所示,已知两个三角形全等,则 ∠α的度数是( )
A.72° B.60° C.58 D.50°
2.如图所示,△ABC≌△BAD,则A和 ,
C和 是对应顶点,若AB=8 cm,BD=7 cm,AD=4 cm,则BC= cm.
3.如图所示,四边形ABCD与四边形A′B′C′D′全等,则∠A′= °,
∠A= °,B′C′= ,AD= .
140
70
12
9
解:∵△ABC≌△DEF,
∴EF=BC,
∠F=∠ACB=180°-∠A-∠B=180°-75°-60°=45°.
∴EF-EC=BC-EC,
即CF=BE=5.
4.如图所示,点B,E,C,F在同一条直线上,△ABC≌△DEF, ∠A=75°,∠B=60°,BE=5.求∠F的度数与CF的长.
5.如图,Rt△ABC≌Rt△CDE,∠B=∠D=90°,且B,C,D三点在一条直线上,求∠ACE的度数.
解:∵Rt△ABC≌Rt△CDE,
∴∠BAC=∠DCE.
在Rt△ABC中,∠B=90°,
∴∠ACB+∠BAC=90°.
∴∠ACB+∠ECD=90°.
∴∠ACE=180°-(∠ACB+∠ECD)=180°-90°=90°.
定义:能够完全重合的两个三角形叫作全等三角形.
性质:全等三角形的对应边相等,对应角相等.
定义:能够完全重合的两个图形叫作全图等形.
性质:全等图形的形状和大小都相等.
图形的全等
全等图形
全等三角形
4.2 全等三角形
1. 理解全等三角形的概念,能识别全等三角形中的对应边、对应角;(重点)
2.掌握全等三角形的性质,能利用全等三角形的性质解决相关问题.(难点)
(1)
(2)
(3)
(4)
都是形状、大小相同的图形.
你能再举出一些类似的例子吗
观察下面各组图形,它们有什么共同特点?
你能找出其他的对应顶点、对应边和对应角吗
点B和点E是对应顶点,点C和点F是对应顶点;
边BC与边EF是对应边,边AC与边DF是对应边;
∠B与∠E是对应角,∠C与∠F是对应角.
如图,像△ABC叠到△DEF上,能够完全重合的两个三角形叫做全等三角形.其中,顶点A与顶点D重合,它们是对应顶点;边AB与边DE重合,它们是对应边;∠A与∠D重合,它们是对应角.
A
B
C
F
E
D
全等的表示方法
“全等”用符号“≌”表示,读作“全等于”.
注意 记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
例如,△ABC与△DEF全等,记作△ABC≌△DEF.
解:对应边:AB和AC,AD和AE,BD和CE;
对应角:∠A和∠A,∠B和∠C,∠ADB和∠AEC.
例1 如图所示,△ABD≌△ACE,AB=AC,写出它们的对应边和对应角.
解:△BOD与△COE的对应边为:BO与CO,OD与OE,BD与CE;
△ADO与△AEO的对应角为:∠DAO与∠EAO,∠ADO与∠AEO,
∠AOD与∠AOE.
1.如图,若△BOD≌△COE,∠B=∠C,指出这两个全等三角形的对应边;若△ADO≌△AEO,指出这两个三角形的对应角.
(1)每人准备两个全等三角形纸片,并画出两个三角形纸片对应边的高.全等三角形对应边的高相等吗 对应边的中线呢 对应的角平分线呢
(1)全等三角形对应边的高、中线以及对应的角平分线都相等.因此,全等三角形的对应线段都相等.
(2)如图,已知△ABC≌△A′B′C′,点D,E分别在BC边、AB边上请在△A′B′C′中画出与线段DE相对应的线段.图中有哪些相等的线段、相等的角?与同伴进行交流.
(2)在边B′C′上作线段B′D′=BD,在边B′A′上作线段B′E′=BE,连接E′D′.
E′
D′
(1)全等三角形的对应边 ,对应角 .
(2)全等三角形的对应线段(对应边的高,对应边的中线,对应角的平分线)都 .
相等
相等
相等
全等三角形的性质:
解:∵△ABC≌△DEF,∠A=32°,∠B=48°.
∴∠D=∠A=32°,∠E=∠B=48°.
在△DEF中,∠D+∠E+∠DFE=180°,
∴∠DFE=100°.
∵△ABC≌△DEF,
∴BC=EF,即BF+FC=EC+FC,
∴BF=EC.
∵BF=3,
∴EC=3.
例2 如图所示,已知△ABC≌△DEF,点E,C,F,B在同一直线上,∠A=32°,∠B=48°,BF=3,求∠DFE的度数和EC的长.
C
2.如图,△ABC≌△CDA,并且BC=DA,那么下列结论错误的是( )
A.∠1=∠2
B.∠ACB=∠DAC
C.AB=AD
D.∠B=∠D
如图所示.
准备一张等边三角形纸片,你能用折纸的办法把它分成两个全等三角形吗 能把它分成三个全等三角形吗 能把它分成四个全等三角形吗 与同伴进行交流。
D
B
D
4
1.如图所示,已知两个三角形全等,则 ∠α的度数是( )
A.72° B.60° C.58 D.50°
2.如图所示,△ABC≌△BAD,则A和 ,
C和 是对应顶点,若AB=8 cm,BD=7 cm,AD=4 cm,则BC= cm.
3.如图所示,四边形ABCD与四边形A′B′C′D′全等,则∠A′= °,
∠A= °,B′C′= ,AD= .
140
70
12
9
解:∵△ABC≌△DEF,
∴EF=BC,
∠F=∠ACB=180°-∠A-∠B=180°-75°-60°=45°.
∴EF-EC=BC-EC,
即CF=BE=5.
4.如图所示,点B,E,C,F在同一条直线上,△ABC≌△DEF, ∠A=75°,∠B=60°,BE=5.求∠F的度数与CF的长.
5.如图,Rt△ABC≌Rt△CDE,∠B=∠D=90°,且B,C,D三点在一条直线上,求∠ACE的度数.
解:∵Rt△ABC≌Rt△CDE,
∴∠BAC=∠DCE.
在Rt△ABC中,∠B=90°,
∴∠ACB+∠BAC=90°.
∴∠ACB+∠ECD=90°.
∴∠ACE=180°-(∠ACB+∠ECD)=180°-90°=90°.
定义:能够完全重合的两个三角形叫作全等三角形.
性质:全等三角形的对应边相等,对应角相等.
定义:能够完全重合的两个图形叫作全图等形.
性质:全等图形的形状和大小都相等.
图形的全等
全等图形
全等三角形
同课章节目录
