4.3探索三角形全等的条件 第1课时 利用“SSS”判定两个三角形全等 课件(共23张PPT)
文档属性
| 名称 | 4.3探索三角形全等的条件 第1课时 利用“SSS”判定两个三角形全等 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-13 06:54:11 | ||
图片预览





文档简介
(共23张PPT)
4.3 探索三角形全等的条件
第1课时 利用“SSS”判定两个三角形全等
1. 了解三角形的稳定性,掌握三角形全等的“SSS”判定,并能应用它判定两个三角形是否全等;(重点)
2.由探索三角形全等条件的过程,体会由操作、归纳获得数学结论的过程.(难点)
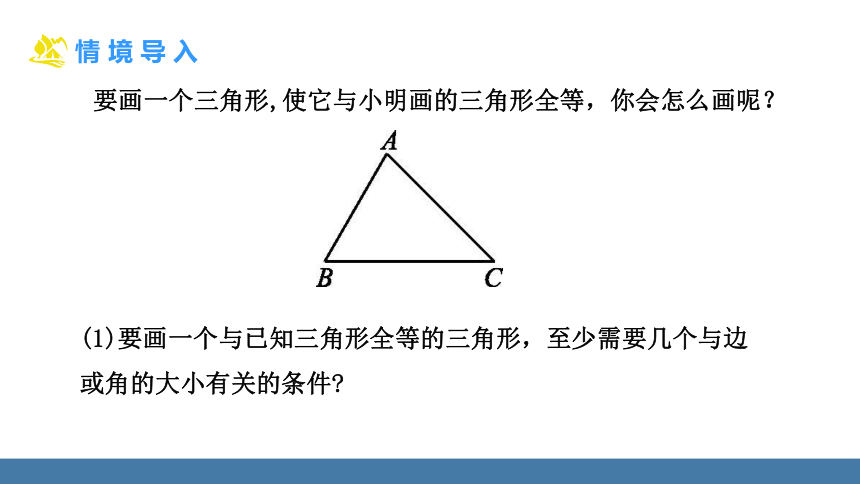
要画一个三角形,使它与小明画的三角形全等,你会怎么画呢?
(1)要画一个与已知三角形全等的三角形,至少需要几个与边或角的大小有关的条件
①只有一条边相等,画出的的三角形不一定全等(如图1).
②只有一个角相等,画出的三角形不一定全等(如图2).
图 1
图 2
(2)只给一个条件(一条边或一个角)可以吗?
结论:有一个条件相等不能保证所画出的三角形一定全等.
30o
3cm
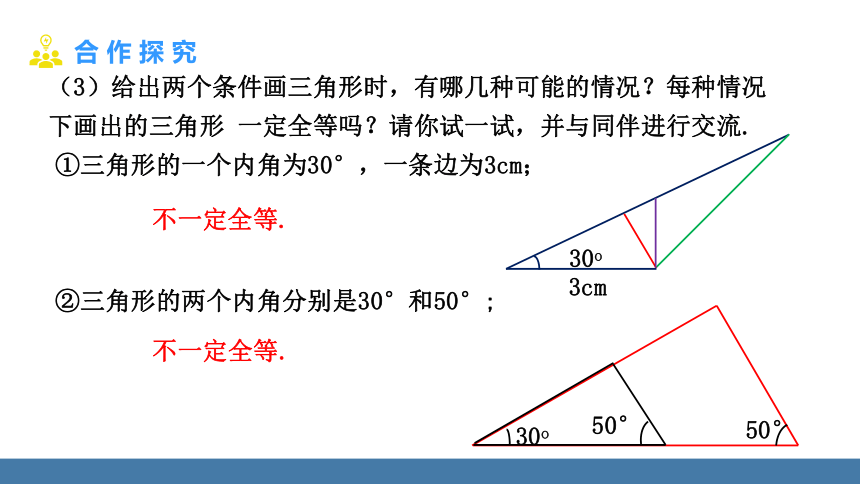
(3)给出两个条件画三角形时,有哪几种可能的情况?每种情况下画出的三角形 一定全等吗?请你试一试,并与同伴进行交流.
①三角形的一个内角为30°,一条边为3cm;
不一定全等.
②三角形的两个内角分别是30°和50°;
50°
50°
30o
不一定全等.
6cm
4cm
结论:有两个条件对应相等不能保证所画出的三角形一定全等.
③三角形的两条边分别为4cm,6cm.
4cm
4cm
不一定全等.
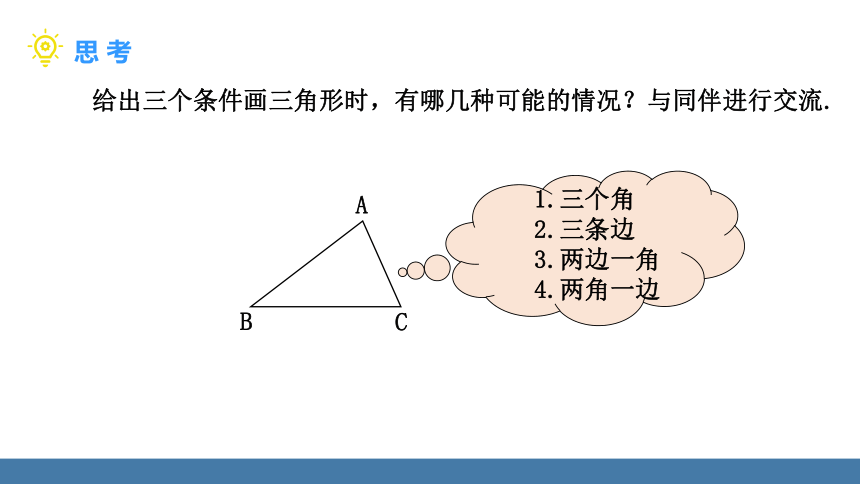
给出三个条件画三角形时,有哪几种可能的情况?与同伴进行交流.
A
B
C
1.三个角
2.三条边
3.两边一角
4.两角一边
(1) 已知一个三角形的三个内角分别为40°,60°和80°,你能画出这个三角形吗?把你画的三角形与同伴画出的进行比较,它们一定全等吗?
40°
60°
80°
40°
60°
80°
三个内角对应相等的两个三角形不一定全等
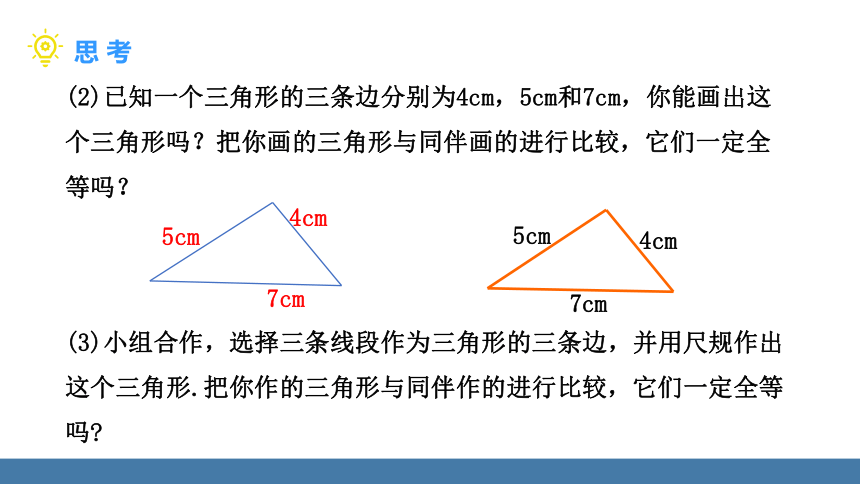
(2)已知一个三角形的三条边分别为4cm,5cm和7cm,你能画出这个三角形吗?把你画的三角形与同伴画的进行比较,它们一定全等吗?
5cm
7cm
4cm
5cm
7cm
4cm
(3)小组合作,选择三条线段作为三角形的三条边,并用尺规作出这个三角形.把你作的三角形与同伴作的进行比较,它们一定全等吗
(SSS)
几何语言:
在△ABC和△A′B′C′中,
△ABC≌△A′B′C′
∴
A'
B'
C'
A
B
C
三边对应相等的两个三角形全等,简写为“边边边”或“SSS”.
AB=A′B′,
BC=B′C′,
AC=A′C′.
“边边边”判定方法
注意:在书写两个三角形全等时对应顶点要写在对应的位置上.
A
C
B
D
解:∵D是BC的中点,
∴BD=CD.
在△ABD与△ACD中,
AB=AC(已知),
BD=CD(已证),
AD=AD(公共边),
∴△ABD≌△ACD(SSS).
例1 如图, △ABC是一个钢架,AB=AC,AD是连接A与BC中点D的支架,试说明:∠B=∠C.
∴∠B=∠C.
1.已知AC=AD,BC=BD,试说明:AB是∠DAC的平分线.
AC=AD( ),
BC=BD( ),
AB=AB( ),
∴△ABC≌△ABD(SSS).
∴∠1=∠2(全等三角形的对应角相等).
∴AB是∠DAC的平分线(角平分线定义).
A
B
C
D
1
2
已知
已知
公共边
解:在△ABC和△ABD中,
通过刚才的探究过程,我们可以总结出“已知三角形的三边,用尺规作这个三角形”的方法和步骤.
如图,已知线a,b,c,用尺规作△ABC,使AB=c,AC=b,BC=a.
a
b
c
作法与示范:
作法 示范
(1)作一条线段BC=a;
(3)连接AB,AC.
△ABC就是所要作的三角形.
B
C
B
C
A
B
C
A
(2)分别以点B,C为圆心,以c,b的长为半径作弧,两弧交于点A.
图1
图2
(3)上面的现象说明了什么?
三角形具有稳定性;四边形没有稳定性.
准备几根硬纸条.
(1)取出三根硬纸条钉成一个三角形(如图1),你能拉动其中两边,使这个三角形的形状发生变化吗?
(2)取出四根硬纸条钉成一个四边形(如图2),拉动其中两边,这个四边形的形状改变了吗?
三角形的稳定性
只要三角形三边的长度确定了,这个三角形的形状和大小就完全确定了.图1是用三根木条钉成的一个三角形框架,它的大小和形状是固定不变的,三角形的这个性质叫作三角形的稳定性.
图2是用四根木条钉成的一个框架,它的形状是可以改变的,因此,四边形具有不稳定性.
你能举几个应用三角形稳定性的例子吗?
C
2.如图所示,人字梯中间一般会设计一个“拉杆”,这样做的道理是( )
A.两点之间,线段最短
B.垂线段最短
C.三角形具有稳定性
D.两直线平行,内错角相等
A
A
2.如图所示,点B,F,C,D在同一直线上,AB=EF,AC=ED,BF=CD,∠A=95°,∠B=25°,则∠D的度数为( )
A.60° B.25°
C.70° D.95°
1.如图所示, 已知在△ABC中,AB=AC,D为BC上一点,BD= CD,则下列结论错误的是( )
A.∠BAC=∠B B.∠BAD=∠CAD
C.AD⊥BC D.∠B=∠C
三角形具有稳定性
(答案不唯一)
AE=AD
3.如图所示,一扇窗户打开后,用窗钩AB可以将其固定,这里所运用的几何原理是 .
4.如图所示,点D,E分别在AB,AC上,AB=AC,BE=CD,要依据“SSS”判定△ABE≌△ACD,还需补充的条件是___ .(填一个即可)
解:(1)∵AD=CF,
∴AD+DC=CF+DC,即AC=DF.
在△ABC和△DEF中,
∵AB=DE,BC=EF,AC=DF,
∴△ABC≌△DEF(SSS).
(2)∵△ABC≌△DEF,
∴∠F=∠ACB.
∵∠A=55°,∠B=88°,
∴∠ACB=180°-(∠A+∠B)
=180°-(55°+88°)=37°.
∴∠F=∠ACB=37°.
5.如图所示,点A,D,C,F在同一条直线上,AD=CF,AB=DE, BC=EF.
(1)试说明:△ABC≌△DEF;
(2)若∠A=55°,∠B=88°,求∠F的度数.
解:如图,连接CD.
在△ACD和△BDC中,
∵AD=BC,AC=BD,CD=DC,
∴△ACD≌△BDC(SSS),
∴∠DAO=∠CBO.
6.如图所示,AD=BC,AC=BD,AC与BD交于点O.
试说明: ∠DAO=∠CBO.
利用SSS判定两个三角形全等
三角形全等的判定方法一
三角形的稳定性
三边分别相等的两个三角形全等(简称“边边边”或“SSS”).
三角形三边长度确定了,这个三角形的形状和大小就完全确定了.
4.3 探索三角形全等的条件
第1课时 利用“SSS”判定两个三角形全等
1. 了解三角形的稳定性,掌握三角形全等的“SSS”判定,并能应用它判定两个三角形是否全等;(重点)
2.由探索三角形全等条件的过程,体会由操作、归纳获得数学结论的过程.(难点)
要画一个三角形,使它与小明画的三角形全等,你会怎么画呢?
(1)要画一个与已知三角形全等的三角形,至少需要几个与边或角的大小有关的条件
①只有一条边相等,画出的的三角形不一定全等(如图1).
②只有一个角相等,画出的三角形不一定全等(如图2).
图 1
图 2
(2)只给一个条件(一条边或一个角)可以吗?
结论:有一个条件相等不能保证所画出的三角形一定全等.
30o
3cm
(3)给出两个条件画三角形时,有哪几种可能的情况?每种情况下画出的三角形 一定全等吗?请你试一试,并与同伴进行交流.
①三角形的一个内角为30°,一条边为3cm;
不一定全等.
②三角形的两个内角分别是30°和50°;
50°
50°
30o
不一定全等.
6cm
4cm
结论:有两个条件对应相等不能保证所画出的三角形一定全等.
③三角形的两条边分别为4cm,6cm.
4cm
4cm
不一定全等.
给出三个条件画三角形时,有哪几种可能的情况?与同伴进行交流.
A
B
C
1.三个角
2.三条边
3.两边一角
4.两角一边
(1) 已知一个三角形的三个内角分别为40°,60°和80°,你能画出这个三角形吗?把你画的三角形与同伴画出的进行比较,它们一定全等吗?
40°
60°
80°
40°
60°
80°
三个内角对应相等的两个三角形不一定全等
(2)已知一个三角形的三条边分别为4cm,5cm和7cm,你能画出这个三角形吗?把你画的三角形与同伴画的进行比较,它们一定全等吗?
5cm
7cm
4cm
5cm
7cm
4cm
(3)小组合作,选择三条线段作为三角形的三条边,并用尺规作出这个三角形.把你作的三角形与同伴作的进行比较,它们一定全等吗
(SSS)
几何语言:
在△ABC和△A′B′C′中,
△ABC≌△A′B′C′
∴
A'
B'
C'
A
B
C
三边对应相等的两个三角形全等,简写为“边边边”或“SSS”.
AB=A′B′,
BC=B′C′,
AC=A′C′.
“边边边”判定方法
注意:在书写两个三角形全等时对应顶点要写在对应的位置上.
A
C
B
D
解:∵D是BC的中点,
∴BD=CD.
在△ABD与△ACD中,
AB=AC(已知),
BD=CD(已证),
AD=AD(公共边),
∴△ABD≌△ACD(SSS).
例1 如图, △ABC是一个钢架,AB=AC,AD是连接A与BC中点D的支架,试说明:∠B=∠C.
∴∠B=∠C.
1.已知AC=AD,BC=BD,试说明:AB是∠DAC的平分线.
AC=AD( ),
BC=BD( ),
AB=AB( ),
∴△ABC≌△ABD(SSS).
∴∠1=∠2(全等三角形的对应角相等).
∴AB是∠DAC的平分线(角平分线定义).
A
B
C
D
1
2
已知
已知
公共边
解:在△ABC和△ABD中,
通过刚才的探究过程,我们可以总结出“已知三角形的三边,用尺规作这个三角形”的方法和步骤.
如图,已知线a,b,c,用尺规作△ABC,使AB=c,AC=b,BC=a.
a
b
c
作法与示范:
作法 示范
(1)作一条线段BC=a;
(3)连接AB,AC.
△ABC就是所要作的三角形.
B
C
B
C
A
B
C
A
(2)分别以点B,C为圆心,以c,b的长为半径作弧,两弧交于点A.
图1
图2
(3)上面的现象说明了什么?
三角形具有稳定性;四边形没有稳定性.
准备几根硬纸条.
(1)取出三根硬纸条钉成一个三角形(如图1),你能拉动其中两边,使这个三角形的形状发生变化吗?
(2)取出四根硬纸条钉成一个四边形(如图2),拉动其中两边,这个四边形的形状改变了吗?
三角形的稳定性
只要三角形三边的长度确定了,这个三角形的形状和大小就完全确定了.图1是用三根木条钉成的一个三角形框架,它的大小和形状是固定不变的,三角形的这个性质叫作三角形的稳定性.
图2是用四根木条钉成的一个框架,它的形状是可以改变的,因此,四边形具有不稳定性.
你能举几个应用三角形稳定性的例子吗?
C
2.如图所示,人字梯中间一般会设计一个“拉杆”,这样做的道理是( )
A.两点之间,线段最短
B.垂线段最短
C.三角形具有稳定性
D.两直线平行,内错角相等
A
A
2.如图所示,点B,F,C,D在同一直线上,AB=EF,AC=ED,BF=CD,∠A=95°,∠B=25°,则∠D的度数为( )
A.60° B.25°
C.70° D.95°
1.如图所示, 已知在△ABC中,AB=AC,D为BC上一点,BD= CD,则下列结论错误的是( )
A.∠BAC=∠B B.∠BAD=∠CAD
C.AD⊥BC D.∠B=∠C
三角形具有稳定性
(答案不唯一)
AE=AD
3.如图所示,一扇窗户打开后,用窗钩AB可以将其固定,这里所运用的几何原理是 .
4.如图所示,点D,E分别在AB,AC上,AB=AC,BE=CD,要依据“SSS”判定△ABE≌△ACD,还需补充的条件是___ .(填一个即可)
解:(1)∵AD=CF,
∴AD+DC=CF+DC,即AC=DF.
在△ABC和△DEF中,
∵AB=DE,BC=EF,AC=DF,
∴△ABC≌△DEF(SSS).
(2)∵△ABC≌△DEF,
∴∠F=∠ACB.
∵∠A=55°,∠B=88°,
∴∠ACB=180°-(∠A+∠B)
=180°-(55°+88°)=37°.
∴∠F=∠ACB=37°.
5.如图所示,点A,D,C,F在同一条直线上,AD=CF,AB=DE, BC=EF.
(1)试说明:△ABC≌△DEF;
(2)若∠A=55°,∠B=88°,求∠F的度数.
解:如图,连接CD.
在△ACD和△BDC中,
∵AD=BC,AC=BD,CD=DC,
∴△ACD≌△BDC(SSS),
∴∠DAO=∠CBO.
6.如图所示,AD=BC,AC=BD,AC与BD交于点O.
试说明: ∠DAO=∠CBO.
利用SSS判定两个三角形全等
三角形全等的判定方法一
三角形的稳定性
三边分别相等的两个三角形全等(简称“边边边”或“SSS”).
三角形三边长度确定了,这个三角形的形状和大小就完全确定了.
同课章节目录
