4.3探索三角形全等的条件 第2课时 利用“ASA”“AAS”判定两个三角形全等 课件(共22张PPT)
文档属性
| 名称 | 4.3探索三角形全等的条件 第2课时 利用“ASA”“AAS”判定两个三角形全等 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-13 06:53:50 | ||
图片预览






文档简介
(共22张PPT)
4.3 探索三角形全等的条件
第2课时 利用“ASA”“AAS”判定两个三角形全等
1.探索并正确理解三角形全等的判定方法“ASA”和“AAS”.(重点)
2.会用三角形全等的判定方法“ASA”和“AAS”证明两个三角形全等.(难点)
如图,小明不慎将一块三角形玻璃打碎为三块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具吗 如果可以,带哪块去合适 你能说明其中理由吗
3
2
1
由前面的讨论我们知道,如果给出一个三角形三条边的长度,那么由此得到的三角形都是全等的.如果已知一个三角形的两角及一边,那么有几种可能的情况呢
有两种情况:一种是两角及其夹边,另一种是两角及其中一角的对边.
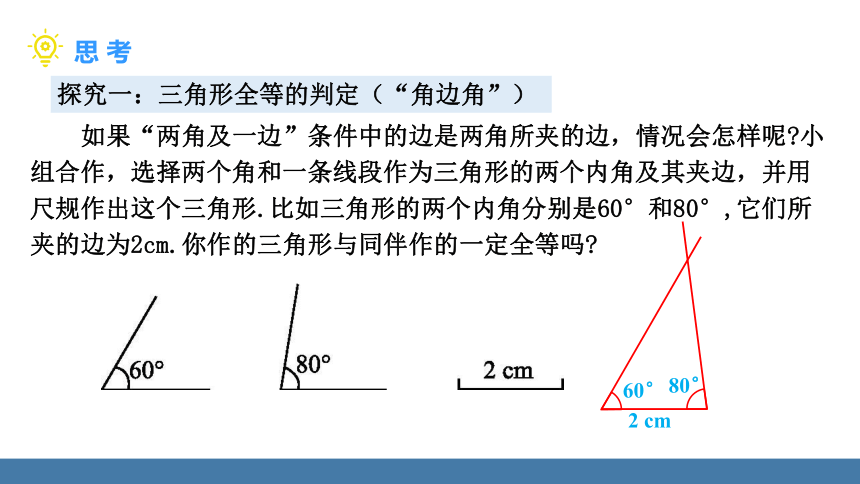
探究一:三角形全等的判定(“角边角”)
如果“两角及一边”条件中的边是两角所夹的边,情况会怎样呢 小组合作,选择两个角和一条线段作为三角形的两个内角及其夹边,并用尺规作出这个三角形.比如三角形的两个内角分别是60°和80°,它们所夹的边为2cm.你作的三角形与同伴作的一定全等吗
2 cm
60°
80°
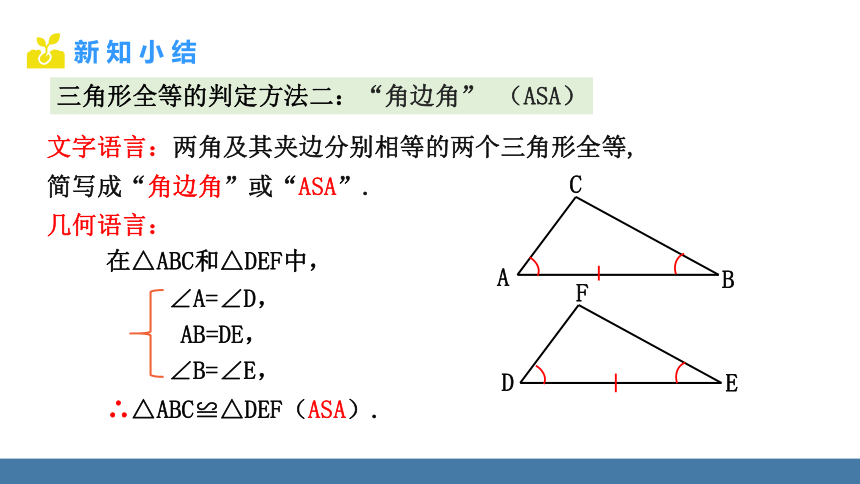
文字语言:两角及其夹边分别相等的两个三角形全等,
简写成“角边角”或“ASA”.
几何语言:
三角形全等的判定方法二:“角边角” (ASA)
A
B
C
D
E
F
在△ABC和△DEF中,
∠A=∠D,
AB=DE,
∠B=∠E,
∴△ABC≌△DEF(ASA).
解:△AEC≌△AED.
理由:∵AB平分∠CAD,
∴∠CAE=∠DAE.
∵∠1=∠2,∠AEC=180°-∠1,∠AED=180°-∠2,
∴∠AEC=∠AED.
例1 如图所示,AB平分∠CAD,点E在AB上,∠1=∠2,△AEC和△AED全等吗 试说明理由.
在△AEC≌△AED中,
∠CAE=∠DAE,
AE=AE,
∠AEC=∠AED
∴△AEC≌△AED(ASA).
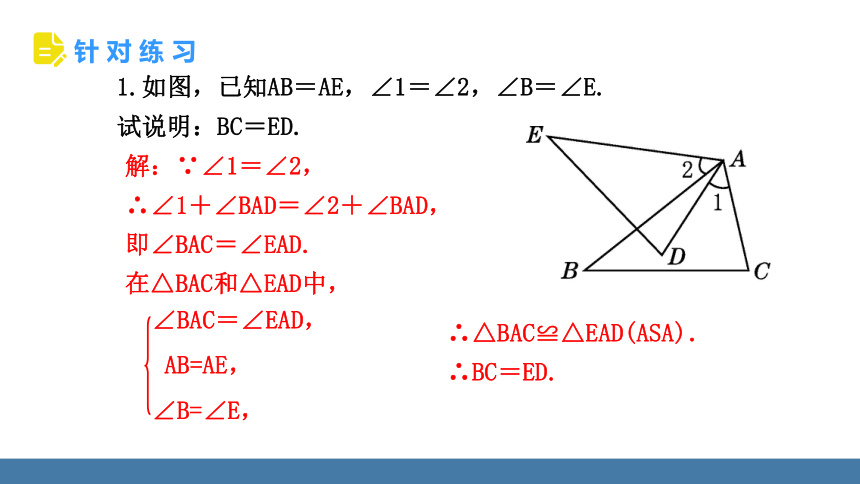
1.如图,已知AB=AE,∠1=∠2,∠B=∠E.
试说明:BC=ED.
解:∵∠1=∠2,
∴∠1+∠BAD=∠2+∠BAD,
即∠BAC=∠EAD.
在△BAC和△EAD中,
∴△BAC≌△EAD(ASA).
∴BC=ED.
∠BAC=∠EAD,
AB=AE,
∠B=∠E,
如图,已知∠α,∠β,线段c,用尺规作△ABC,使∠A =∠α,
∠B =∠β,AB = c.
β
c
α
回顾上述作图过程,请你总结“已知三角形的两角及其夹边,用尺规作这个三角形”的方法和步骤.
作法:
(1)作∠DAF =∠α.
(2)在射线AF上截取线段AB=c;
(3)以B为顶点,以BA为一边,作∠ABE=∠β,BE交AD于点C.△ABC就是所要作的三角形.
A
F
D
B
A
D
F
C
A
B
D
F
E
议一议:(1)如果“两角及一边”条件中的边是其中一角的对边,情况会怎样呢 你能将它转化为探究一中的条件吗
探究二:三角形全等的判定(“角角边”)
解:(1)如果两个角都确定了,那么第三个内角一定是确定的,如此一来,可将“两角及其中一角的对边”转化为“两角及其夹边”.
你能证明你的结论吗?
∴△ABC≌△DEF(ASA).
∴∠C=180°-∠A-∠B.
同理 ∠F=180°-∠D-∠E.
在△ABC和△DEF中,
(2)在△ABC和△DEF中, ∠A=∠D, ∠B=∠E ,BC=EF,△ABC与△DEF全等吗?能利用角边角条件证明你的结论吗?
解:
在△ABC中,∠A+∠B+∠C=180°.
又∠A=∠D,∠B=∠E,
∴∠C=∠F.
∠B=∠E,
BC=EF,
∠C=∠F.
A
B
C
D
E
F
文字语言:两角分别相等且其中一组等角的对边相等的两个三角形全等. (简写成“角角边”或“AAS”)
几何语言:
A
B
C
D
E
F
三角形全等的判定方法三:“角角边” (AAS)
在△ABC和△DEF中,
∠A=∠D,
∠B=∠E.
BC=EF,
∴△ABC≌△DEF(AAS).
证明:∵AC是∠BAE的平分线,
∴∠BAC=∠DAE.
∴△BAC≌△DAE(AAS).
在△BAC和△DAE中,
例2 如图所示,AC是∠BAE的平分线,D是线段AC上的一点,∠C=∠E,AB=AD.试说明:△BAC≌△DAE.
∠BAC=∠DAE,
∠C=∠E,
AB=AD,
说明三角形全等时寻找等角的方法:
(1)公共角相等、对顶角相等、直角相等;
(2)等角加(减)等角,其和(差)相等;
(3)同角(或等角)的余角(或补角)相等;
(4)根据角平分线、平行线得角相等.
知识归纳
解:△ABC≌△ADE.
理由:∵∠1=∠2,
∴∠1+∠DAC=∠2+∠DAC,
即∠BAC=∠DAE.
2.如图所示,已知∠C=∠E,∠1=∠2,AB=AD,△ABC和△ADE全等吗 试说明理由.
在△ABC和△ADE中,
∠BAC=∠DAE,
∠C=∠E,
AB=AD,
∴△ABC≌△ADE(AAS).
B
D
2.如图所示,D是AB延长线上一点,DF交AC于点E,AE=CE, FC∥AB,若AB=3,CF=5,则BD的长是( )
A.0.5 B.1
C.1.5 D.2
1.如图所示,∠ADB=∠CDB,∠ABD=∠CBD,则直接判定△ABD≌△CBD的依据是 ( )
A.SSS B.ASA
C.AAS D.以上均不正确
3.如图所示,AE=AD,∠B=∠C,则△ABD≌ ,理由是 .
△ACE
AAS
4.如图所示,∠1=∠2,BC=EC,请补充一个条件: ,能直接根据“AAS”判定△ABC≌△DEC.
∠A=∠D
5.如图所示,AC⊥BC于点C,DE⊥AC于点E,AD⊥AB于点A.若BC=AE,AD=5,则AB= .
5
第5题
第6题
第7题
解:∵AB⊥AC,AD⊥AE,
∴∠BAE+∠CAE=90°,∠BAE+∠BAD=90°.
∴∠CAE=∠BAD.
在△ABD和△ACE中,
∵∠BAD=∠CAE,AB=AC,∠ABD=∠ACE,
∴△ABD≌△ACE(ASA).
∴BD=CE.
6.如图所示,AB=AC,AB⊥AC,AD⊥AE,且∠ABD=∠ACE.
试说明:BD=CE.
解:(1)∵AB⊥BC,∴∠ABC=90°.
又∵AD∥BC,∴∠BAD=90°,
即∠BAF+∠DAE=90°.
∵DE⊥AC,∴∠DEA=90°,
∴∠DAE+∠ADE=90°.∴∠ADE=∠BAF.
∵BF⊥AC,∠ABF=63°,
∴∠ADE=∠BAF=90°- 63°=27°.
7.如图所示,AD∥BC,AB⊥BC,AB=AD,连接AC,过点D作DE⊥AC于点E,过点B作BF⊥AC于点F.
(1)若∠ABF=63°,求∠ADE的度数;
(2)DE=BF+EF.
理由:∵DE⊥AC,BF⊥AC,
∴∠BFA=∠AED=90°.
在△ABF和△DAE中,
∵∠BFA=∠AED,∠BAF=∠ADE,AB=DA,
∴△ABF≌△DAE(AAS),
∴BF=AE,AF=DE.
∵AF=AE+EF,
∴DE=BF+EF.
(2)请写出线段BF,EF,DE三者之间的数量关系,并说明理由.
利用“ASA”“AAS”判定两个三角形全等
三角形全等的判定方法二
说明三角形全等时寻找等角的方法
两角及其夹边分别相等的两个三角形全等,简写成“角边角”或“ASA”.
(1)公共角相等、对顶角相等、直角相等;
(2)等角加(减)等角,其和(差)相等;
(3)同角(或等角)的余角(或补角)相等;
(4)根据角平分线、平行线得角相等.
三角形全等的判定方法三
两角分别相等且其中一组等角的对边相等的两个三角形全等,简写成“角角边”或“AAS”.
4.3 探索三角形全等的条件
第2课时 利用“ASA”“AAS”判定两个三角形全等
1.探索并正确理解三角形全等的判定方法“ASA”和“AAS”.(重点)
2.会用三角形全等的判定方法“ASA”和“AAS”证明两个三角形全等.(难点)
如图,小明不慎将一块三角形玻璃打碎为三块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具吗 如果可以,带哪块去合适 你能说明其中理由吗
3
2
1
由前面的讨论我们知道,如果给出一个三角形三条边的长度,那么由此得到的三角形都是全等的.如果已知一个三角形的两角及一边,那么有几种可能的情况呢
有两种情况:一种是两角及其夹边,另一种是两角及其中一角的对边.
探究一:三角形全等的判定(“角边角”)
如果“两角及一边”条件中的边是两角所夹的边,情况会怎样呢 小组合作,选择两个角和一条线段作为三角形的两个内角及其夹边,并用尺规作出这个三角形.比如三角形的两个内角分别是60°和80°,它们所夹的边为2cm.你作的三角形与同伴作的一定全等吗
2 cm
60°
80°
文字语言:两角及其夹边分别相等的两个三角形全等,
简写成“角边角”或“ASA”.
几何语言:
三角形全等的判定方法二:“角边角” (ASA)
A
B
C
D
E
F
在△ABC和△DEF中,
∠A=∠D,
AB=DE,
∠B=∠E,
∴△ABC≌△DEF(ASA).
解:△AEC≌△AED.
理由:∵AB平分∠CAD,
∴∠CAE=∠DAE.
∵∠1=∠2,∠AEC=180°-∠1,∠AED=180°-∠2,
∴∠AEC=∠AED.
例1 如图所示,AB平分∠CAD,点E在AB上,∠1=∠2,△AEC和△AED全等吗 试说明理由.
在△AEC≌△AED中,
∠CAE=∠DAE,
AE=AE,
∠AEC=∠AED
∴△AEC≌△AED(ASA).
1.如图,已知AB=AE,∠1=∠2,∠B=∠E.
试说明:BC=ED.
解:∵∠1=∠2,
∴∠1+∠BAD=∠2+∠BAD,
即∠BAC=∠EAD.
在△BAC和△EAD中,
∴△BAC≌△EAD(ASA).
∴BC=ED.
∠BAC=∠EAD,
AB=AE,
∠B=∠E,
如图,已知∠α,∠β,线段c,用尺规作△ABC,使∠A =∠α,
∠B =∠β,AB = c.
β
c
α
回顾上述作图过程,请你总结“已知三角形的两角及其夹边,用尺规作这个三角形”的方法和步骤.
作法:
(1)作∠DAF =∠α.
(2)在射线AF上截取线段AB=c;
(3)以B为顶点,以BA为一边,作∠ABE=∠β,BE交AD于点C.△ABC就是所要作的三角形.
A
F
D
B
A
D
F
C
A
B
D
F
E
议一议:(1)如果“两角及一边”条件中的边是其中一角的对边,情况会怎样呢 你能将它转化为探究一中的条件吗
探究二:三角形全等的判定(“角角边”)
解:(1)如果两个角都确定了,那么第三个内角一定是确定的,如此一来,可将“两角及其中一角的对边”转化为“两角及其夹边”.
你能证明你的结论吗?
∴△ABC≌△DEF(ASA).
∴∠C=180°-∠A-∠B.
同理 ∠F=180°-∠D-∠E.
在△ABC和△DEF中,
(2)在△ABC和△DEF中, ∠A=∠D, ∠B=∠E ,BC=EF,△ABC与△DEF全等吗?能利用角边角条件证明你的结论吗?
解:
在△ABC中,∠A+∠B+∠C=180°.
又∠A=∠D,∠B=∠E,
∴∠C=∠F.
∠B=∠E,
BC=EF,
∠C=∠F.
A
B
C
D
E
F
文字语言:两角分别相等且其中一组等角的对边相等的两个三角形全等. (简写成“角角边”或“AAS”)
几何语言:
A
B
C
D
E
F
三角形全等的判定方法三:“角角边” (AAS)
在△ABC和△DEF中,
∠A=∠D,
∠B=∠E.
BC=EF,
∴△ABC≌△DEF(AAS).
证明:∵AC是∠BAE的平分线,
∴∠BAC=∠DAE.
∴△BAC≌△DAE(AAS).
在△BAC和△DAE中,
例2 如图所示,AC是∠BAE的平分线,D是线段AC上的一点,∠C=∠E,AB=AD.试说明:△BAC≌△DAE.
∠BAC=∠DAE,
∠C=∠E,
AB=AD,
说明三角形全等时寻找等角的方法:
(1)公共角相等、对顶角相等、直角相等;
(2)等角加(减)等角,其和(差)相等;
(3)同角(或等角)的余角(或补角)相等;
(4)根据角平分线、平行线得角相等.
知识归纳
解:△ABC≌△ADE.
理由:∵∠1=∠2,
∴∠1+∠DAC=∠2+∠DAC,
即∠BAC=∠DAE.
2.如图所示,已知∠C=∠E,∠1=∠2,AB=AD,△ABC和△ADE全等吗 试说明理由.
在△ABC和△ADE中,
∠BAC=∠DAE,
∠C=∠E,
AB=AD,
∴△ABC≌△ADE(AAS).
B
D
2.如图所示,D是AB延长线上一点,DF交AC于点E,AE=CE, FC∥AB,若AB=3,CF=5,则BD的长是( )
A.0.5 B.1
C.1.5 D.2
1.如图所示,∠ADB=∠CDB,∠ABD=∠CBD,则直接判定△ABD≌△CBD的依据是 ( )
A.SSS B.ASA
C.AAS D.以上均不正确
3.如图所示,AE=AD,∠B=∠C,则△ABD≌ ,理由是 .
△ACE
AAS
4.如图所示,∠1=∠2,BC=EC,请补充一个条件: ,能直接根据“AAS”判定△ABC≌△DEC.
∠A=∠D
5.如图所示,AC⊥BC于点C,DE⊥AC于点E,AD⊥AB于点A.若BC=AE,AD=5,则AB= .
5
第5题
第6题
第7题
解:∵AB⊥AC,AD⊥AE,
∴∠BAE+∠CAE=90°,∠BAE+∠BAD=90°.
∴∠CAE=∠BAD.
在△ABD和△ACE中,
∵∠BAD=∠CAE,AB=AC,∠ABD=∠ACE,
∴△ABD≌△ACE(ASA).
∴BD=CE.
6.如图所示,AB=AC,AB⊥AC,AD⊥AE,且∠ABD=∠ACE.
试说明:BD=CE.
解:(1)∵AB⊥BC,∴∠ABC=90°.
又∵AD∥BC,∴∠BAD=90°,
即∠BAF+∠DAE=90°.
∵DE⊥AC,∴∠DEA=90°,
∴∠DAE+∠ADE=90°.∴∠ADE=∠BAF.
∵BF⊥AC,∠ABF=63°,
∴∠ADE=∠BAF=90°- 63°=27°.
7.如图所示,AD∥BC,AB⊥BC,AB=AD,连接AC,过点D作DE⊥AC于点E,过点B作BF⊥AC于点F.
(1)若∠ABF=63°,求∠ADE的度数;
(2)DE=BF+EF.
理由:∵DE⊥AC,BF⊥AC,
∴∠BFA=∠AED=90°.
在△ABF和△DAE中,
∵∠BFA=∠AED,∠BAF=∠ADE,AB=DA,
∴△ABF≌△DAE(AAS),
∴BF=AE,AF=DE.
∵AF=AE+EF,
∴DE=BF+EF.
(2)请写出线段BF,EF,DE三者之间的数量关系,并说明理由.
利用“ASA”“AAS”判定两个三角形全等
三角形全等的判定方法二
说明三角形全等时寻找等角的方法
两角及其夹边分别相等的两个三角形全等,简写成“角边角”或“ASA”.
(1)公共角相等、对顶角相等、直角相等;
(2)等角加(减)等角,其和(差)相等;
(3)同角(或等角)的余角(或补角)相等;
(4)根据角平分线、平行线得角相等.
三角形全等的判定方法三
两角分别相等且其中一组等角的对边相等的两个三角形全等,简写成“角角边”或“AAS”.
同课章节目录
