4.3探索三角形全等的条件 第4课时 判定三角形全等的综合选择 课件(共17张PPT)
文档属性
| 名称 | 4.3探索三角形全等的条件 第4课时 判定三角形全等的综合选择 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-13 07:09:06 | ||
图片预览



文档简介
(共17张PPT)
4.3 探索三角形全等的条件
第4课时 判定三角形全等的综合选择
1.通过讨论区分开全等三角形的四种判定方法.(重点)
2.能灵活地运用这四种方法来判定两个三角形全等.(难点)
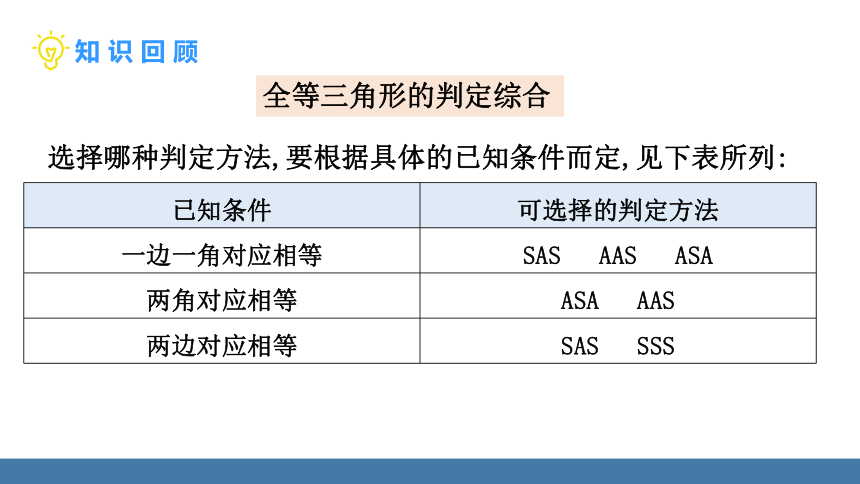
选择哪种判定方法,要根据具体的已知条件而定,见下表所列:
已知条件 可选择的判定方法
一边一角对应相等 SAS AAS ASA
两角对应相等 ASA AAS
两边对应相等 SAS SSS
全等三角形的判定综合
例1 如图,AB∥CD.并且AB=CD,那么△ABD与△CDB全等吗?请说明理由.
解:∵ AB∥CD,
根据“两直线平行,内错角相等”,
∴∠1=∠2.
在△ABD与△CDB中,
∵AB=CD,∠1=∠2,BD=DB,
根据三角形全等的判定条件“SAS”,∴△ABD≌△CDB.
A
D
B
C
2
1
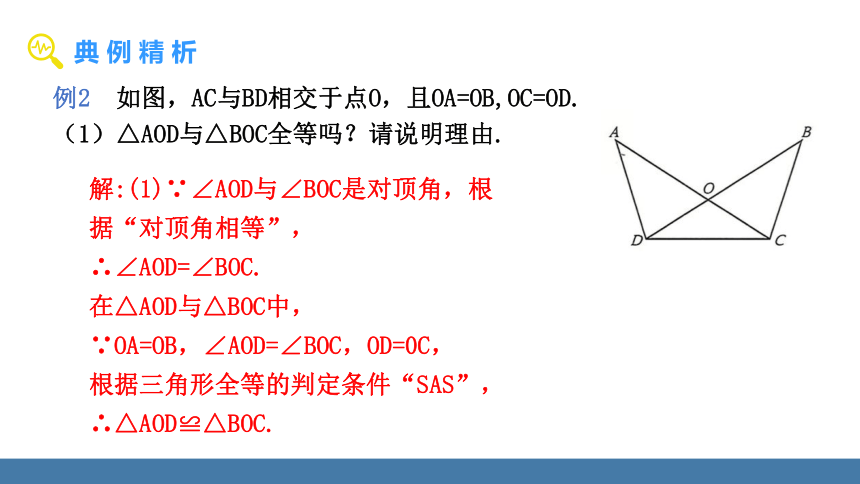
例2 如图,AC与BD相交于点O,且OA=OB,OC=OD.
(1)△AOD与△BOC全等吗?请说明理由.
解:(1)∵∠AOD与∠BOC是对顶角,根据“对顶角相等”,
∴∠AOD=∠BOC.
在△AOD与△BOC中,
∵OA=OB,∠AOD=∠BOC,OD=0C,
根据三角形全等的判定条件“SAS”,
∴△AOD≌△BOC.
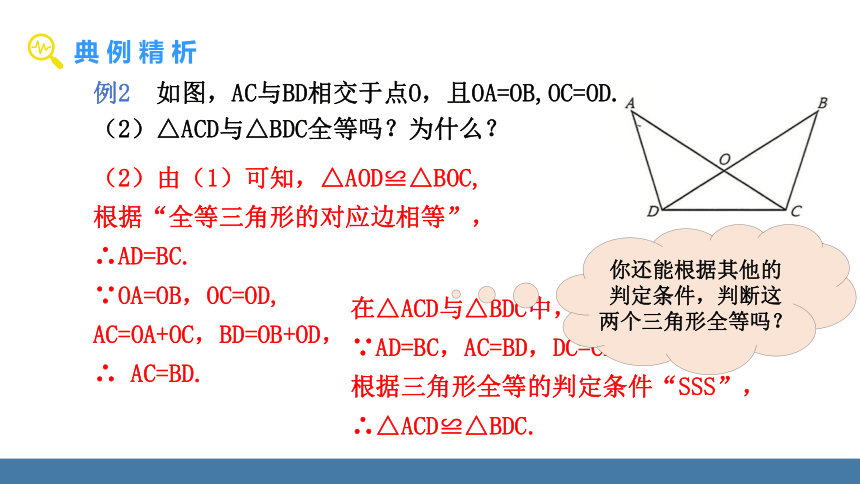
例2 如图,AC与BD相交于点O,且OA=OB,OC=OD.
(2)△ACD与△BDC全等吗?为什么?
(2)由(1)可知,△AOD≌△BOC,
根据“全等三角形的对应边相等”,
∴AD=BC.
∵OA=OB,OC=OD,
AC=OA+OC,BD=OB+OD,
∴ AC=BD.
在△ACD与△BDC中,
∵AD=BC,AC=BD,DC=CD,
根据三角形全等的判定条件“SSS”,
∴△ACD≌△BDC.
你还能根据其他的判定条件,判断这两个三角形全等吗?
D
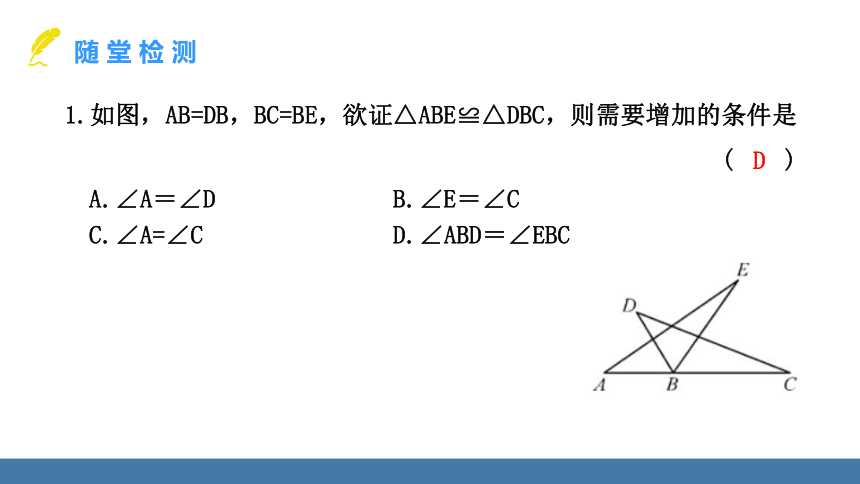
1.如图,AB=DB,BC=BE,欲证△ABE≌△DBC,则需要增加的条件是 ( )
A.∠A=∠D B.∠E=∠C
C.∠A=∠C D.∠ABD=∠EBC
2.如图,在△ABC和△DEF中,点B, F, C, D在同一条直线上,已知∠A=∠D,AB=DE,添加以下条件,不能判定△ABC≌△DEF的是( )
A.∠B=∠E
B.AC=DF
C.∠ACD=∠BFE
D.BC=EF
D
3.如图,在△ABC中,∠ACB=90°,点D为AC边上一点,ED⊥AC,CE⊥AB,AB=CE.若BC=2,DE=5,则线段AD的长为_______.
3
4.如图,已知点A,C在线段BD两侧,AB=AD,CB=CD,线段AC, BD相交于点O.下列结论:①∠ABC=∠ADC;②AC⊥BD;③AC平分∠BAD;④OB=OD.其中正确的是____________.(填序号)
①②③④
5.如图,有一张三角形纸片ABC,∠B=∠C=x°,按下列方案用剪刀沿着箭头方向剪开,可能得不到全等三角形纸片的是( )
C
6.如图,已知点B,F,C,E在直线 l 上,点A,D在 l 异侧,且AC∥DF,AC=DF.
(1)请你添加一个适当的条件:__________,使得△ABC≌△DEF.
∠A=∠D
(2)若BE=20,BF=6,求FC的长度.
解:∵△ABC≌△DEF,
∴BC=EF.
∴BC-CF=EF-CF.∴BF=CE.
∵BE=20,BF=6,∴CE=BF=6.
∴FC=BE-BF-CE=20-6-6=8.
7.如图,点 A,B,C,D 在同一条直线上,BE//DF,∠A=∠F,AB=FD. 试说明:AE=FC.
解:∵BE//DF,
∴∠ABE =∠D,
在△ABE 和△FDC 中,
∠ABE = ∠D,
AB = FD,
∠A = ∠F,
∴△ABE≌△FDC(ASA)
∴AE = FC .
F
A
C
B
D
E
8.如图,在四边形ABCD中,AB∥CD,在BD上取两点E,F,使BF=DE,连接AE,CF.
(1)若AE∥CF,试说明△ABE≌△CDF;
解:∵AB∥CD,
∴∠ABE=∠CDF.
∵AE∥CF,
∴∠AEB=∠CFD.
∵BF=DE,
∴BF+EF=DE+EF,
即BE=DF.
在△ABE和△CDF中,
∠ABE=∠CDF,
BE=DF,
∠AEB=∠CFD,
∴△ABE≌△CDF(ASA).
(2)在(1)的条件下,连接AF,CE,试判断AF与CE有怎样的数量关系,并说明理由.
解:AF=CE.理由如下:
∵△ABE≌△CDF,
∴AB=CD.
在△ABF和△CDE中,
AB=CD,
∠ABD=∠CDB,
BF=DE,
∴△ABF≌△CDE(SAS).
∴AF=CE.
SSS
判定三角形全等的方法
三边对应相等
ASA
AAS
两角和其中一角的对边对应相等
两角和它们的夹边对应相等
SAS
两边和它们的夹角对应相等
4.3 探索三角形全等的条件
第4课时 判定三角形全等的综合选择
1.通过讨论区分开全等三角形的四种判定方法.(重点)
2.能灵活地运用这四种方法来判定两个三角形全等.(难点)
选择哪种判定方法,要根据具体的已知条件而定,见下表所列:
已知条件 可选择的判定方法
一边一角对应相等 SAS AAS ASA
两角对应相等 ASA AAS
两边对应相等 SAS SSS
全等三角形的判定综合
例1 如图,AB∥CD.并且AB=CD,那么△ABD与△CDB全等吗?请说明理由.
解:∵ AB∥CD,
根据“两直线平行,内错角相等”,
∴∠1=∠2.
在△ABD与△CDB中,
∵AB=CD,∠1=∠2,BD=DB,
根据三角形全等的判定条件“SAS”,∴△ABD≌△CDB.
A
D
B
C
2
1
例2 如图,AC与BD相交于点O,且OA=OB,OC=OD.
(1)△AOD与△BOC全等吗?请说明理由.
解:(1)∵∠AOD与∠BOC是对顶角,根据“对顶角相等”,
∴∠AOD=∠BOC.
在△AOD与△BOC中,
∵OA=OB,∠AOD=∠BOC,OD=0C,
根据三角形全等的判定条件“SAS”,
∴△AOD≌△BOC.
例2 如图,AC与BD相交于点O,且OA=OB,OC=OD.
(2)△ACD与△BDC全等吗?为什么?
(2)由(1)可知,△AOD≌△BOC,
根据“全等三角形的对应边相等”,
∴AD=BC.
∵OA=OB,OC=OD,
AC=OA+OC,BD=OB+OD,
∴ AC=BD.
在△ACD与△BDC中,
∵AD=BC,AC=BD,DC=CD,
根据三角形全等的判定条件“SSS”,
∴△ACD≌△BDC.
你还能根据其他的判定条件,判断这两个三角形全等吗?
D
1.如图,AB=DB,BC=BE,欲证△ABE≌△DBC,则需要增加的条件是 ( )
A.∠A=∠D B.∠E=∠C
C.∠A=∠C D.∠ABD=∠EBC
2.如图,在△ABC和△DEF中,点B, F, C, D在同一条直线上,已知∠A=∠D,AB=DE,添加以下条件,不能判定△ABC≌△DEF的是( )
A.∠B=∠E
B.AC=DF
C.∠ACD=∠BFE
D.BC=EF
D
3.如图,在△ABC中,∠ACB=90°,点D为AC边上一点,ED⊥AC,CE⊥AB,AB=CE.若BC=2,DE=5,则线段AD的长为_______.
3
4.如图,已知点A,C在线段BD两侧,AB=AD,CB=CD,线段AC, BD相交于点O.下列结论:①∠ABC=∠ADC;②AC⊥BD;③AC平分∠BAD;④OB=OD.其中正确的是____________.(填序号)
①②③④
5.如图,有一张三角形纸片ABC,∠B=∠C=x°,按下列方案用剪刀沿着箭头方向剪开,可能得不到全等三角形纸片的是( )
C
6.如图,已知点B,F,C,E在直线 l 上,点A,D在 l 异侧,且AC∥DF,AC=DF.
(1)请你添加一个适当的条件:__________,使得△ABC≌△DEF.
∠A=∠D
(2)若BE=20,BF=6,求FC的长度.
解:∵△ABC≌△DEF,
∴BC=EF.
∴BC-CF=EF-CF.∴BF=CE.
∵BE=20,BF=6,∴CE=BF=6.
∴FC=BE-BF-CE=20-6-6=8.
7.如图,点 A,B,C,D 在同一条直线上,BE//DF,∠A=∠F,AB=FD. 试说明:AE=FC.
解:∵BE//DF,
∴∠ABE =∠D,
在△ABE 和△FDC 中,
∠ABE = ∠D,
AB = FD,
∠A = ∠F,
∴△ABE≌△FDC(ASA)
∴AE = FC .
F
A
C
B
D
E
8.如图,在四边形ABCD中,AB∥CD,在BD上取两点E,F,使BF=DE,连接AE,CF.
(1)若AE∥CF,试说明△ABE≌△CDF;
解:∵AB∥CD,
∴∠ABE=∠CDF.
∵AE∥CF,
∴∠AEB=∠CFD.
∵BF=DE,
∴BF+EF=DE+EF,
即BE=DF.
在△ABE和△CDF中,
∠ABE=∠CDF,
BE=DF,
∠AEB=∠CFD,
∴△ABE≌△CDF(ASA).
(2)在(1)的条件下,连接AF,CE,试判断AF与CE有怎样的数量关系,并说明理由.
解:AF=CE.理由如下:
∵△ABE≌△CDF,
∴AB=CD.
在△ABF和△CDE中,
AB=CD,
∠ABD=∠CDB,
BF=DE,
∴△ABF≌△CDE(SAS).
∴AF=CE.
SSS
判定三角形全等的方法
三边对应相等
ASA
AAS
两角和其中一角的对边对应相等
两角和它们的夹边对应相等
SAS
两边和它们的夹角对应相等
同课章节目录
