5.1轴对称及其性质 课件(共31张PPT)
文档属性
| 名称 | 5.1轴对称及其性质 课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-13 00:00:00 | ||
图片预览











文档简介
(共31张PPT)
第五章 图形的轴对称
轴对称现象在生活中广泛存在:无论是气势恢宏的大型建筑还是生活中随处可见的各种标志,无论是传统的民间艺术还是现代的工业设计,都不乏轴对称的身影。你能发现生活中的轴对称图形吗 对于轴对称,你有怎样的认识
本章将在小学学习的基础上,进一步研究轴对称的性质,从轴对称的视角探索等腰三角形、线段和角的一些性质,开展搜集、欣赏、设计轴对称图案的活动。在这一过程中,你将感知并描述平面图形轴对称的规律,积累研究平面图形性质的经验,初步形成合乎逻辑地思考、表达与交流的习惯,发展空间观念、几何直观和推理能力等。
5.1 轴对称及其性质
1.在生活实例中认识轴对称图形及两个图形轴对称,探索并掌握轴对称的性质;(重点)
2.会利用轴对称的性质作对称点、对称图形、对称轴等,体验数学与生活的联系、提高审美观.(难点)
观察图中的图片和图形,它们有什么共同特点?
你还能举出一些类似的例子吗?与同伴进行交流.
如果一个平面图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫作轴对称图形,这条直线叫作对称轴.
轴对称图形
对称轴
a
m
解:除了第4个图都是轴对称图形.第1个、第3个图有一条对称轴,第2个图有两条对称轴,第6个图有四条对称轴,第5个图有六条对称轴.
观察图中的图形,哪些图形是轴对称图形 如果是轴对称图形,请找出它的对称轴.
方法归纳
判断一个图形是不是轴对称图形的关键是看能否找到一条直线,将图形沿着这条直线折叠后,直线两旁的部分能够互相重合,若能找到,则该图形就是轴对称图形,否则就不是轴对称图形.
圆的对称轴最多,有无数条.
1.找出下列各图形中的对称轴,并说明哪一个图形的对称轴最多.
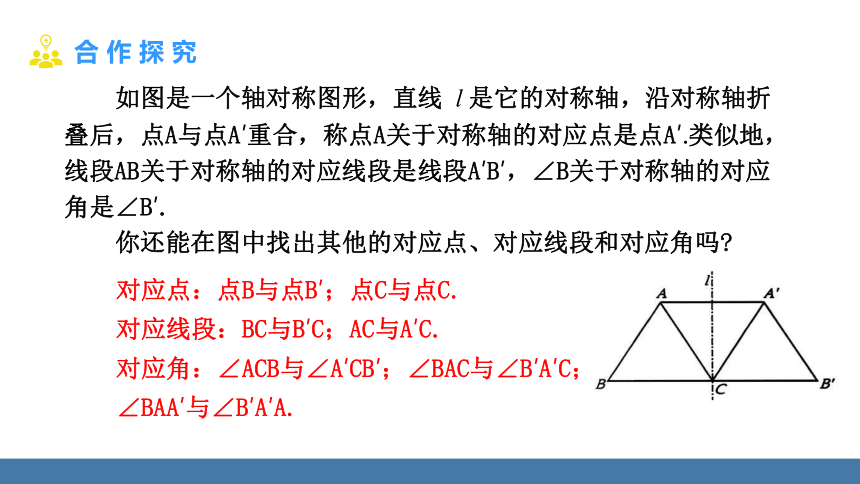
如图是一个轴对称图形,直线 l 是它的对称轴,沿对称轴折叠后,点A与点A′重合,称点A关于对称轴的对应点是点A′.类似地,线段AB关于对称轴的对应线段是线段A′B′,∠B关于对称轴的对应角是∠B′.
你还能在图中找出其他的对应点、对应线段和对应角吗
对应点:点B与点B′;点C与点C.
对应线段:BC与B′C;AC与A′C.
对应角:∠ACB与∠A′CB′;∠BAC与∠B′A′C;
∠BAA′与∠B′A′A.
如图是一个轴对称图形,直线 l 是它的对称轴.观察这个图形,回答下列问题:
(1)在图中任意选一组对应线段,这两条线段之间有什么关系 为什么
解:(1)BC与B′C′为对应线段;BC=B′C′
理由:因为该图为轴对称图形,对称轴两旁的部分为全等图形,对应线段相等.
如图是一个轴对称图形,直线 l 是它的对称轴.观察这个图形,回答下列问题:
(2)在图中任意选一组对应角,这两个角之间有什么关系 说说你的理由.
(2)∠1与∠2为对应角;∠1=∠2
理由:因为该图为轴对称图形,对称轴两旁的部分为全等图形,对应角相等.
如图是一个轴对称图形,直线 l 是它的对称轴.观察这个图形,回答下列问题:
(3)连接对应点A与A′,线段 AA′与对称轴之间有什么关系 连接其他任意一组对应点再试一试.
(3)线段 AA′与对称轴直线 l 垂直,并且直线 l 平分线段 AA′ .
如果两个平面图形沿一条直线折叠后能够完全重合,那么称这两个图形成轴对称,这条直线叫作这两个图形的对称轴.
观察下图中的每组图案,你发现了什么?
B
D
C
A
2.下列四组图片中有哪几组图形成轴对称?
轴对称图形和两个图形成轴对称的区别与联系:
轴对称图形 两个图形成轴对称
图形
区别
联系
一个图形具有的特殊形状
两个全等图形的特殊的位置关系
1.都是沿着某条直线折叠后能重合.
2.可以互相转化.
(1)两个“14”有什么关系?
关于直线 l 成轴对称.
如图,将一张长方形形的纸对折,然后用笔尖扎出“14”这个数字,再将纸打开后铺平.
(2)对应线段之间有什么关系 对应角之间有什么关系 连接对应点的线段与对称轴 l 之间有什么关系 请举例说明,并与同伴进行交流.
在轴对称图形或两个成轴对称的图形中,对应点所连的线段被对称轴垂直平分,对应线段相等,对应角相等.
轴对称的性质
解析:根据正方形的轴对称性可得,阴影部分的面积等于正方形ABCD面积的一半.
∵正方形ABCD的边长为4cm,
∴S阴影=42÷2=8(cm2).故选B.
B
例1 如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为( )
A.4cm2 B.8cm2 C.12cm2 D.16cm2
解析:∵这种滑翔伞的形状是左右成轴对称的四边形ABCD,其中∠BAD=150°,∠B=40°,
∴∠D=40°.
∴∠BCD=360°-150°-40°-40°=130°.
A
3.如图,一种滑翔伞的形状是左右成轴对称的四边形ABCD,其中∠BAD=150°,∠B=40°,则∠BCD的度数是( )
A.130°
B.150°
C.40°
D.65°
例2 下图是一个图案的一半,其中的虚线是这个图案的对称轴,画出这个图案的另一半.
A
B
M
N
O
P
解:如图,延长 AO至 A′,使 OA′=0A;延长 BN至 B′,使 NB′=NB;
A′
B′
依次连接 MA′,MB′,A′B′,A′P,B′P.这样画出的图形就是这个图形的另一半.
画轴对称图形的步骤
(1)找:找出已知图形的关键点;
(2)作:过关键点作对称轴的垂线段并延长,使延长线的长度等于垂线段的长度,即可确定关键点的对应点;
(3)连:按已知图形的方式连接各关键点的对应点,即可得到与已知图形关于对称轴对称的图形.
解:如图所示,△A′B′C′即为所求.
4.如图所示,画出与△ABC关于直线 l 成轴对称的三角形.
A
1.下列几组图案中成轴对称的有( )
A.3组 B.2组 C.1组 D.0组
①③
2.如图所示的四个汽车标志图案中是轴对称图形的有 (填序号).
7cm
60
56cm2
80°
3
3.如图所示,△ABC与△DEF关于直线MN对称.
(1)若AB=7 cm,则DE= ;
(2)若∠A=70°,∠B=50°,则∠F= °;
(3)若S△DEF=56 cm2,则S△ABC= .
4.右图中的两个四边形关于某直线对称,根据图形提供的条件,可得x= ,y= .
5.如图,在方格纸中画了一棵树的一半,请你以树干为对称轴画出树的另一半.
解:(1)∵△ABC与△DEF关于直线MN对称,
∴直线MN垂直平分线段AD.
(2)∵△ABC与△DEF关于直线MN对称,
∴△ABC≌△DEF,∴∠F=∠C=90°.
6.如图所示,△ABC与△DEF关于直线MN对称,其中∠C=90°, AC=8 cm,DE=10 cm,BC=6 cm.
(1)连接AD,线段AD与直线MN的关系是什么
(2)求∠F的度数;
(3)求△ABC的周长和△DEF的面积.
(3)由题意得AB=DE=10 cm,
∴C△ABC=6+8+10=24(cm);S△DEF=S△ABC=×6×8=24(cm2).
解:∵点P关于OM的对称点是G,点P关于ON的对称点是H,
∴PA=GA,PB=HB,
∴PA+AB+PB=GA+AB+HB=GH=10cm,
即△PAB的周长为10cm.
7.如图所示,∠MON内有一点P,点P关于OM的对称点是G,点P关于ON的对称点是H,连接GH分别交OM, ON于A,B两点.若GH的长为10 cm,求△PAB的周长.
如果一个平面图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫作轴对称图形,这条直线叫作对称轴.
如果两个平面图形沿一条直线对折后能够完全重合,那么称这两个图形成轴对称.
轴对称及其性质
定义
性质
在轴对称图形或两个成轴对称的图形中,对应点所连的线段被对称轴垂直平分,对应线段相等,对应角相等.
画轴对称图形的步骤:(1)找;(2)作;(3)连.
第五章 图形的轴对称
轴对称现象在生活中广泛存在:无论是气势恢宏的大型建筑还是生活中随处可见的各种标志,无论是传统的民间艺术还是现代的工业设计,都不乏轴对称的身影。你能发现生活中的轴对称图形吗 对于轴对称,你有怎样的认识
本章将在小学学习的基础上,进一步研究轴对称的性质,从轴对称的视角探索等腰三角形、线段和角的一些性质,开展搜集、欣赏、设计轴对称图案的活动。在这一过程中,你将感知并描述平面图形轴对称的规律,积累研究平面图形性质的经验,初步形成合乎逻辑地思考、表达与交流的习惯,发展空间观念、几何直观和推理能力等。
5.1 轴对称及其性质
1.在生活实例中认识轴对称图形及两个图形轴对称,探索并掌握轴对称的性质;(重点)
2.会利用轴对称的性质作对称点、对称图形、对称轴等,体验数学与生活的联系、提高审美观.(难点)
观察图中的图片和图形,它们有什么共同特点?
你还能举出一些类似的例子吗?与同伴进行交流.
如果一个平面图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫作轴对称图形,这条直线叫作对称轴.
轴对称图形
对称轴
a
m
解:除了第4个图都是轴对称图形.第1个、第3个图有一条对称轴,第2个图有两条对称轴,第6个图有四条对称轴,第5个图有六条对称轴.
观察图中的图形,哪些图形是轴对称图形 如果是轴对称图形,请找出它的对称轴.
方法归纳
判断一个图形是不是轴对称图形的关键是看能否找到一条直线,将图形沿着这条直线折叠后,直线两旁的部分能够互相重合,若能找到,则该图形就是轴对称图形,否则就不是轴对称图形.
圆的对称轴最多,有无数条.
1.找出下列各图形中的对称轴,并说明哪一个图形的对称轴最多.
如图是一个轴对称图形,直线 l 是它的对称轴,沿对称轴折叠后,点A与点A′重合,称点A关于对称轴的对应点是点A′.类似地,线段AB关于对称轴的对应线段是线段A′B′,∠B关于对称轴的对应角是∠B′.
你还能在图中找出其他的对应点、对应线段和对应角吗
对应点:点B与点B′;点C与点C.
对应线段:BC与B′C;AC与A′C.
对应角:∠ACB与∠A′CB′;∠BAC与∠B′A′C;
∠BAA′与∠B′A′A.
如图是一个轴对称图形,直线 l 是它的对称轴.观察这个图形,回答下列问题:
(1)在图中任意选一组对应线段,这两条线段之间有什么关系 为什么
解:(1)BC与B′C′为对应线段;BC=B′C′
理由:因为该图为轴对称图形,对称轴两旁的部分为全等图形,对应线段相等.
如图是一个轴对称图形,直线 l 是它的对称轴.观察这个图形,回答下列问题:
(2)在图中任意选一组对应角,这两个角之间有什么关系 说说你的理由.
(2)∠1与∠2为对应角;∠1=∠2
理由:因为该图为轴对称图形,对称轴两旁的部分为全等图形,对应角相等.
如图是一个轴对称图形,直线 l 是它的对称轴.观察这个图形,回答下列问题:
(3)连接对应点A与A′,线段 AA′与对称轴之间有什么关系 连接其他任意一组对应点再试一试.
(3)线段 AA′与对称轴直线 l 垂直,并且直线 l 平分线段 AA′ .
如果两个平面图形沿一条直线折叠后能够完全重合,那么称这两个图形成轴对称,这条直线叫作这两个图形的对称轴.
观察下图中的每组图案,你发现了什么?
B
D
C
A
2.下列四组图片中有哪几组图形成轴对称?
轴对称图形和两个图形成轴对称的区别与联系:
轴对称图形 两个图形成轴对称
图形
区别
联系
一个图形具有的特殊形状
两个全等图形的特殊的位置关系
1.都是沿着某条直线折叠后能重合.
2.可以互相转化.
(1)两个“14”有什么关系?
关于直线 l 成轴对称.
如图,将一张长方形形的纸对折,然后用笔尖扎出“14”这个数字,再将纸打开后铺平.
(2)对应线段之间有什么关系 对应角之间有什么关系 连接对应点的线段与对称轴 l 之间有什么关系 请举例说明,并与同伴进行交流.
在轴对称图形或两个成轴对称的图形中,对应点所连的线段被对称轴垂直平分,对应线段相等,对应角相等.
轴对称的性质
解析:根据正方形的轴对称性可得,阴影部分的面积等于正方形ABCD面积的一半.
∵正方形ABCD的边长为4cm,
∴S阴影=42÷2=8(cm2).故选B.
B
例1 如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为( )
A.4cm2 B.8cm2 C.12cm2 D.16cm2
解析:∵这种滑翔伞的形状是左右成轴对称的四边形ABCD,其中∠BAD=150°,∠B=40°,
∴∠D=40°.
∴∠BCD=360°-150°-40°-40°=130°.
A
3.如图,一种滑翔伞的形状是左右成轴对称的四边形ABCD,其中∠BAD=150°,∠B=40°,则∠BCD的度数是( )
A.130°
B.150°
C.40°
D.65°
例2 下图是一个图案的一半,其中的虚线是这个图案的对称轴,画出这个图案的另一半.
A
B
M
N
O
P
解:如图,延长 AO至 A′,使 OA′=0A;延长 BN至 B′,使 NB′=NB;
A′
B′
依次连接 MA′,MB′,A′B′,A′P,B′P.这样画出的图形就是这个图形的另一半.
画轴对称图形的步骤
(1)找:找出已知图形的关键点;
(2)作:过关键点作对称轴的垂线段并延长,使延长线的长度等于垂线段的长度,即可确定关键点的对应点;
(3)连:按已知图形的方式连接各关键点的对应点,即可得到与已知图形关于对称轴对称的图形.
解:如图所示,△A′B′C′即为所求.
4.如图所示,画出与△ABC关于直线 l 成轴对称的三角形.
A
1.下列几组图案中成轴对称的有( )
A.3组 B.2组 C.1组 D.0组
①③
2.如图所示的四个汽车标志图案中是轴对称图形的有 (填序号).
7cm
60
56cm2
80°
3
3.如图所示,△ABC与△DEF关于直线MN对称.
(1)若AB=7 cm,则DE= ;
(2)若∠A=70°,∠B=50°,则∠F= °;
(3)若S△DEF=56 cm2,则S△ABC= .
4.右图中的两个四边形关于某直线对称,根据图形提供的条件,可得x= ,y= .
5.如图,在方格纸中画了一棵树的一半,请你以树干为对称轴画出树的另一半.
解:(1)∵△ABC与△DEF关于直线MN对称,
∴直线MN垂直平分线段AD.
(2)∵△ABC与△DEF关于直线MN对称,
∴△ABC≌△DEF,∴∠F=∠C=90°.
6.如图所示,△ABC与△DEF关于直线MN对称,其中∠C=90°, AC=8 cm,DE=10 cm,BC=6 cm.
(1)连接AD,线段AD与直线MN的关系是什么
(2)求∠F的度数;
(3)求△ABC的周长和△DEF的面积.
(3)由题意得AB=DE=10 cm,
∴C△ABC=6+8+10=24(cm);S△DEF=S△ABC=×6×8=24(cm2).
解:∵点P关于OM的对称点是G,点P关于ON的对称点是H,
∴PA=GA,PB=HB,
∴PA+AB+PB=GA+AB+HB=GH=10cm,
即△PAB的周长为10cm.
7.如图所示,∠MON内有一点P,点P关于OM的对称点是G,点P关于ON的对称点是H,连接GH分别交OM, ON于A,B两点.若GH的长为10 cm,求△PAB的周长.
如果一个平面图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫作轴对称图形,这条直线叫作对称轴.
如果两个平面图形沿一条直线对折后能够完全重合,那么称这两个图形成轴对称.
轴对称及其性质
定义
性质
在轴对称图形或两个成轴对称的图形中,对应点所连的线段被对称轴垂直平分,对应线段相等,对应角相等.
画轴对称图形的步骤:(1)找;(2)作;(3)连.
同课章节目录
