5.2简单的轴对称图形 第1课时 等腰三角形的性质 课件(共21张PPT)
文档属性
| 名称 | 5.2简单的轴对称图形 第1课时 等腰三角形的性质 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-13 07:05:49 | ||
图片预览








文档简介
(共21张PPT)
5.2 简单的轴对称图形
第1课时 等腰三角形的性质
1. 理解并掌握等腰三角形的性质;(重点)
2. 探索并掌握等腰三角形的轴对称性及其相关性质,能初步运用其解决有关问题.(难点)
等腰三角形是生活中常见的图形,它有什么特征 下面我们一起来探究!
观察下列图片,它们有什么共同的特征?
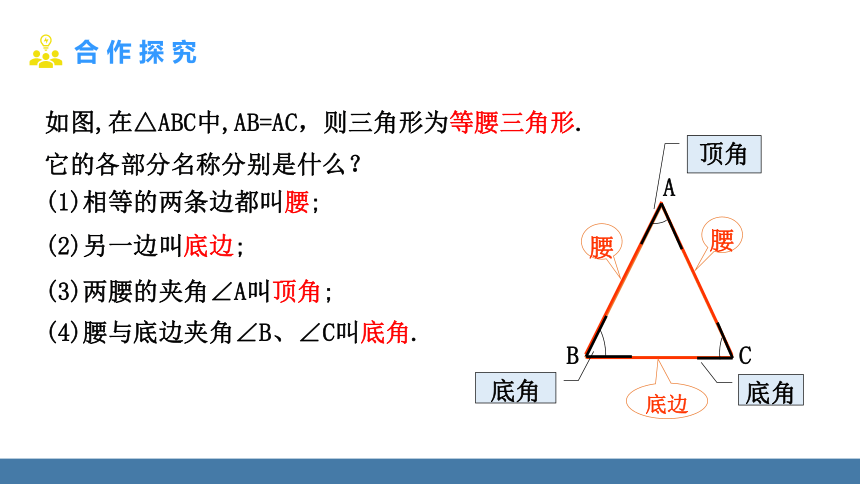
如图,在△ABC中,AB=AC,则三角形为等腰三角形.
它的各部分名称分别是什么?
A
B
C
(1)相等的两条边都叫腰;
腰
腰
底边
(2)另一边叫底边;
顶角
底角
底角
(3)两腰的夹角∠A叫顶角;
(4)腰与底边夹角∠B、∠C叫底角.
解:(1)等腰三角形是轴对称图形.
如图,将等腰三角形沿过顶点的直线折叠,使得两底角重合,折痕所在的直线即为等腰三角形的对称轴.
两腰、两底角等都相等.
(1)等腰三角形是轴对称图形吗 如果是,沿它的对称轴折叠,你能发现哪些相等的线段和相等的角?
(3)你认为等腰三角形有哪些特征 与同伴进行交流
(3)等腰三角形底边上的中线和底边上的高所在的直线是它的对称轴.
(2)等腰三角形的对称轴是一条怎样的直线 你是如何描述的?
(2)等腰三角形顶角平分线所在的直线是它的对称轴.
(1)等腰三角形是 图形.
(2)等腰三角形顶角的 、底边上的 、底边上的 重合(也称“三线合一”),它们所在的直线都是等腰三角形的 .
(3)等腰三角形的两个底角 .
轴对称
平分线
中线
高
对称轴
相等
等腰三角形的性质
解:设这个等腰三角形顶角的度数为 x°,则底角的度数为 2x°.根据“三角形三个内角的和等于 180°”,得
x+2x+2x=180.
解得 x=36.
2×36=72.
所以,这个三角形的三个内角分别是 36°,72°,72°.
例1 已知一个等腰三角形的底角是顶角的2倍,求它的各个内角的度数.
1.等腰三角形的一个内角是50°,则这个三角形的底角的大小是( )
A.65°或50° B.80°或40°
C.65°或80° D.50°或80°
解析:当50°的角是底角时,三角形的底角就是50°;当50°的角是顶角时,两底角相等,根据三角形的内角和定理易得底角是65°.
A
分类讨论思想.
解:∵AB=AC,AD是BC边上的中线,
∴∠BAD=∠CAD,AD⊥BC.
又∵BE⊥AC,
∴∠CBE+∠C=∠CAD+∠C=90°.
∴∠CBE=∠CAD.
∴∠CBE=∠BAD.
2.如图所示,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E.试说明:∠CBE=∠BAD.
(1)等腰三角形“三线合一”的性质是说明角相等、线段相等和垂直关系的既重要又简便的方法;
(2)在等腰三角形中,作“三线”中的“一线”,利用“三线合一”的性质是解决有关等腰三角形问题的常见方法.
方法归纳
C
B
A
如图 ,△ABC是一个等腰三角形,直线l 是它的对称轴.请在△ABC中画出以直线 l 为对称轴的一组对应点、一组对应线段、一组对应角,你能发现哪些相等的线段、相等的角,以及形状、大小完全相同的图形
解:(1)等边三角形有3条对称轴.
(1)等边三角形有几条对称轴
(2)你能发现它的哪些特征
(2)等边三角形是轴对称图形,三个内角都为60°,三条边都相等.
等边三角形是特殊的等腰三角形,具有等腰三角形的所有的性质.
l
(1)等边三角形是轴对称图形,有 条对称轴.
(2)等边三角形每条边都 ,每个角都 ,都等于 .
(3)等边三角形每条边上的中线、高、该边所对角的平分线重合
(“三线合一”).
三
相等
相等
60°
等边三角形的性质
解:∵△ABC是等边三角形,
∴ ∠ABC=∠ACB=60°,AB=BC.
∴∠ACE=120°.
∵D为AC的中点,AB=BC,
∵CE=CD,
∴∠DBC=∠E.
例2 如图所示,在等边三角形ABC的AC边上取中点D,BC的延长线上取一点E,使CE=CD.试说明:∠DBC=∠E.
解: ∵△ABC是等边三角形,D是BC的中点,
∴AD⊥BC,∠DAC=30°.
∴∠ADC=90°.
∵AE=AD,
∴∠ADE=(180°-∠DAC)=75°.
∴∠EDC=∠ADC-∠ADE=90°-75°=15°.
3.如图所示,△ABC是等边三角形,D是BC的中点,点E在AC上,且AE=AD,求∠EDC的度数.
2.等腰三角形的一个角是50°,则它一腰上的高与底边的夹角是( )
A.25° B.40°
C.25°或40° D.不能确定
C
D
1.如图所示,在△ABC中,AB=AC,D是BC的中点,下列结论中不正确的是( )
A.∠B=∠C B.AD⊥BC
C.AD平分∠BAC D.AB=2BD
50°
7
5.若等腰三角形一腰上的高与另一腰的夹角的度数为20°,则该等腰三角形顶角的度数为 .
110°或70°
3.如图所示,小艾同学坐在秋千上,秋千旋转了80°,小艾同学的位置也从A点运动到了A′点,则∠OAA′的度数为 .
4.如图所示,在△ABC中,AB=AC,点D,E都在边BC上,∠BAD= ∠CAE,若BD=7,则CE的长为 .
6.如图所示,在△ABC中,AB=AC,∠A=40°,BD平分∠ABC,求∠BDC的度数.
解:∵AB=AC,∠A=40°,
∴∠ABC=∠C=(180°-∠A)=70°.
∵BD平分∠ABC,
∴∠DBC=∠ABC=35°.
∴∠BDC=180°-∠DBC-∠C=75°.
解:(1)∵AB=AC,
∴∠C=∠ABC.
∵∠C=36°,
∴∠ABC=36°.
∵BD=CD,AB=AC,
∴AD⊥BC.
∴∠ADB=90°.
∴∠BAD=90°-36°=54°.
7.如图所示,在△ABC中,AB=AC,D是BC边的中点,连接AD, BE平分∠ABC交AC于点E,过点E作EF∥BC交AB于点F.
(1)若∠C=36°,求∠BAD的度数;
7.如图所示,在△ABC中,AB=AC,D是BC边的中点,连接AD, BE平分∠ABC交AC于点E,过点E作EF∥BC交AB于点F.
(2)试说明:∠FBE=∠FEB.
(2)∵BE平分∠ABC,
∴∠ABE=∠CBE.
∵EF∥BC,
∴∠FEB=∠CBE.
∴∠FBE=∠FEB.
简单的轴对称图形-等腰三角形
等腰三角形的两个底角相等.
等腰三角形的顶角的平分线、底边上的中线、底边上的高重合(也称“三线合一”),它们所在的直线都是等腰三角形的对称轴.
等腰三角形是轴对称图形.
等腰三角形的性质
等边三角形的性质
(1)等边三角形是轴对称图形,有3条对称轴.
(2)等边三角形每条边都相等,每个角都相等,都等于60°.
(3)等边三角形每条边上的中线、高、该边所对角的平分线重合(“三线合一”).
5.2 简单的轴对称图形
第1课时 等腰三角形的性质
1. 理解并掌握等腰三角形的性质;(重点)
2. 探索并掌握等腰三角形的轴对称性及其相关性质,能初步运用其解决有关问题.(难点)
等腰三角形是生活中常见的图形,它有什么特征 下面我们一起来探究!
观察下列图片,它们有什么共同的特征?
如图,在△ABC中,AB=AC,则三角形为等腰三角形.
它的各部分名称分别是什么?
A
B
C
(1)相等的两条边都叫腰;
腰
腰
底边
(2)另一边叫底边;
顶角
底角
底角
(3)两腰的夹角∠A叫顶角;
(4)腰与底边夹角∠B、∠C叫底角.
解:(1)等腰三角形是轴对称图形.
如图,将等腰三角形沿过顶点的直线折叠,使得两底角重合,折痕所在的直线即为等腰三角形的对称轴.
两腰、两底角等都相等.
(1)等腰三角形是轴对称图形吗 如果是,沿它的对称轴折叠,你能发现哪些相等的线段和相等的角?
(3)你认为等腰三角形有哪些特征 与同伴进行交流
(3)等腰三角形底边上的中线和底边上的高所在的直线是它的对称轴.
(2)等腰三角形的对称轴是一条怎样的直线 你是如何描述的?
(2)等腰三角形顶角平分线所在的直线是它的对称轴.
(1)等腰三角形是 图形.
(2)等腰三角形顶角的 、底边上的 、底边上的 重合(也称“三线合一”),它们所在的直线都是等腰三角形的 .
(3)等腰三角形的两个底角 .
轴对称
平分线
中线
高
对称轴
相等
等腰三角形的性质
解:设这个等腰三角形顶角的度数为 x°,则底角的度数为 2x°.根据“三角形三个内角的和等于 180°”,得
x+2x+2x=180.
解得 x=36.
2×36=72.
所以,这个三角形的三个内角分别是 36°,72°,72°.
例1 已知一个等腰三角形的底角是顶角的2倍,求它的各个内角的度数.
1.等腰三角形的一个内角是50°,则这个三角形的底角的大小是( )
A.65°或50° B.80°或40°
C.65°或80° D.50°或80°
解析:当50°的角是底角时,三角形的底角就是50°;当50°的角是顶角时,两底角相等,根据三角形的内角和定理易得底角是65°.
A
分类讨论思想.
解:∵AB=AC,AD是BC边上的中线,
∴∠BAD=∠CAD,AD⊥BC.
又∵BE⊥AC,
∴∠CBE+∠C=∠CAD+∠C=90°.
∴∠CBE=∠CAD.
∴∠CBE=∠BAD.
2.如图所示,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E.试说明:∠CBE=∠BAD.
(1)等腰三角形“三线合一”的性质是说明角相等、线段相等和垂直关系的既重要又简便的方法;
(2)在等腰三角形中,作“三线”中的“一线”,利用“三线合一”的性质是解决有关等腰三角形问题的常见方法.
方法归纳
C
B
A
如图 ,△ABC是一个等腰三角形,直线l 是它的对称轴.请在△ABC中画出以直线 l 为对称轴的一组对应点、一组对应线段、一组对应角,你能发现哪些相等的线段、相等的角,以及形状、大小完全相同的图形
解:(1)等边三角形有3条对称轴.
(1)等边三角形有几条对称轴
(2)你能发现它的哪些特征
(2)等边三角形是轴对称图形,三个内角都为60°,三条边都相等.
等边三角形是特殊的等腰三角形,具有等腰三角形的所有的性质.
l
(1)等边三角形是轴对称图形,有 条对称轴.
(2)等边三角形每条边都 ,每个角都 ,都等于 .
(3)等边三角形每条边上的中线、高、该边所对角的平分线重合
(“三线合一”).
三
相等
相等
60°
等边三角形的性质
解:∵△ABC是等边三角形,
∴ ∠ABC=∠ACB=60°,AB=BC.
∴∠ACE=120°.
∵D为AC的中点,AB=BC,
∵CE=CD,
∴∠DBC=∠E.
例2 如图所示,在等边三角形ABC的AC边上取中点D,BC的延长线上取一点E,使CE=CD.试说明:∠DBC=∠E.
解: ∵△ABC是等边三角形,D是BC的中点,
∴AD⊥BC,∠DAC=30°.
∴∠ADC=90°.
∵AE=AD,
∴∠ADE=(180°-∠DAC)=75°.
∴∠EDC=∠ADC-∠ADE=90°-75°=15°.
3.如图所示,△ABC是等边三角形,D是BC的中点,点E在AC上,且AE=AD,求∠EDC的度数.
2.等腰三角形的一个角是50°,则它一腰上的高与底边的夹角是( )
A.25° B.40°
C.25°或40° D.不能确定
C
D
1.如图所示,在△ABC中,AB=AC,D是BC的中点,下列结论中不正确的是( )
A.∠B=∠C B.AD⊥BC
C.AD平分∠BAC D.AB=2BD
50°
7
5.若等腰三角形一腰上的高与另一腰的夹角的度数为20°,则该等腰三角形顶角的度数为 .
110°或70°
3.如图所示,小艾同学坐在秋千上,秋千旋转了80°,小艾同学的位置也从A点运动到了A′点,则∠OAA′的度数为 .
4.如图所示,在△ABC中,AB=AC,点D,E都在边BC上,∠BAD= ∠CAE,若BD=7,则CE的长为 .
6.如图所示,在△ABC中,AB=AC,∠A=40°,BD平分∠ABC,求∠BDC的度数.
解:∵AB=AC,∠A=40°,
∴∠ABC=∠C=(180°-∠A)=70°.
∵BD平分∠ABC,
∴∠DBC=∠ABC=35°.
∴∠BDC=180°-∠DBC-∠C=75°.
解:(1)∵AB=AC,
∴∠C=∠ABC.
∵∠C=36°,
∴∠ABC=36°.
∵BD=CD,AB=AC,
∴AD⊥BC.
∴∠ADB=90°.
∴∠BAD=90°-36°=54°.
7.如图所示,在△ABC中,AB=AC,D是BC边的中点,连接AD, BE平分∠ABC交AC于点E,过点E作EF∥BC交AB于点F.
(1)若∠C=36°,求∠BAD的度数;
7.如图所示,在△ABC中,AB=AC,D是BC边的中点,连接AD, BE平分∠ABC交AC于点E,过点E作EF∥BC交AB于点F.
(2)试说明:∠FBE=∠FEB.
(2)∵BE平分∠ABC,
∴∠ABE=∠CBE.
∵EF∥BC,
∴∠FEB=∠CBE.
∴∠FBE=∠FEB.
简单的轴对称图形-等腰三角形
等腰三角形的两个底角相等.
等腰三角形的顶角的平分线、底边上的中线、底边上的高重合(也称“三线合一”),它们所在的直线都是等腰三角形的对称轴.
等腰三角形是轴对称图形.
等腰三角形的性质
等边三角形的性质
(1)等边三角形是轴对称图形,有3条对称轴.
(2)等边三角形每条边都相等,每个角都相等,都等于60°.
(3)等边三角形每条边上的中线、高、该边所对角的平分线重合(“三线合一”).
同课章节目录
