5.2简单的轴对称图形 第3课时 角平分线的性质 课件(共18张PPT)
文档属性
| 名称 | 5.2简单的轴对称图形 第3课时 角平分线的性质 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-13 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
5.2 简单的轴对称图形
第3课时 角平分线的性质
1. 通过操作、验证等方式,探究并掌握角平分线的性质定理;(重点)
2. 会用尺规作角平分线,能运用角的平分线性质解决简单的几何问题.(难点)
角是生活中常见的图形.角是轴对称图形吗
如果是,你能找出它的对称轴吗?
A
O
B
如图所示,将∠AOB对折,你发现了什么
角是 图形, 是它的对称轴.
轴对称
角平分线所在的直线
角的对称性
如图 5-19,OP是∠AOB的平分线,点C是OP上的任意一点.在∠AOB中画出以OP所在直线为对称轴的一组对应点D和D′连接CD和CD′.
(1)你认为线段CD和CD′之间有什么关系 说说你的理由.
解:(1)CD=CD′
理由:∵OP是∠AOB的平分线,
∴∠AOP=∠BOP.
∵点D和D′关于OP所在直线对称,
∴OD=OD′.
∵OC=OC,
∴△CDO≌△CD′O(SAS).
∴CD=CD′.
(2)特别地,当CD⊥OA时(如图5-20),CD′与OB有怎样的位置关系 为什么 此时,线段CD和CD′之间还有(1)中的关系吗
(2)CD′⊥OB.因为点D和点D′关于OP所在直线对称.
线段CD和CD′依旧相等.
由此你能得到什么结论
角平分线上的点到这个角的两边的距离相等.
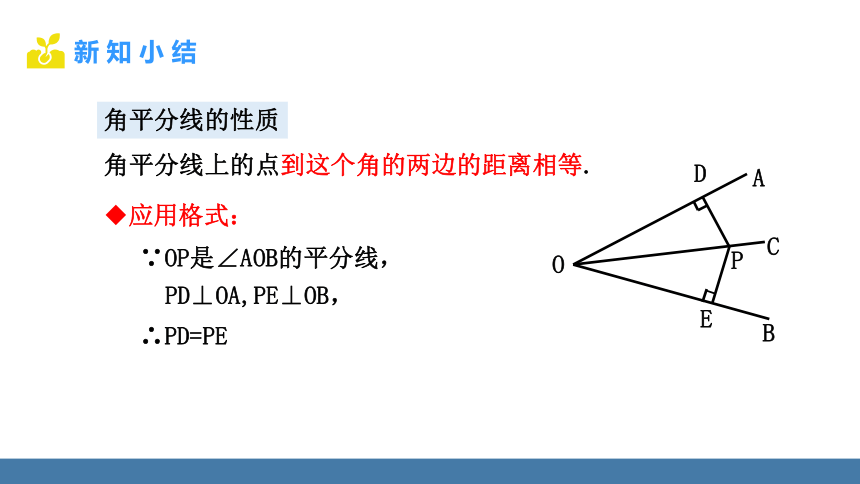
角平分线的性质
应用格式:
∵OP是∠AOB的平分线,
∴PD=PE
PD⊥OA,PE⊥OB,
B
A
D
O
P
E
C
解:OB=OC.
理由如下:
∵点O在∠BAC的平分线上,OD⊥AC,OE⊥AB,
∴OE=OD,∠BEO=∠CDO=90°.
在△BEO和△CDO中,
∵∠BEO=∠CDO,OE=OD,∠EOB=∠DOC,
∴△BEO≌△CDO(ASA).
∴OB=OC.
例1 如图所示,点O在∠BAC的平分线上,OD⊥AC,OE⊥AB,垂足分别为D,E,DO,EO的延长线分别交AE,AD的延长线于点B,C,OB与OC相等吗?为什么?
解:过点E作EF⊥AB于点F.
∵∠C=∠D=90°,
∵AE,BE分别平分∠DAB,∠ABC,
∴CE=EF,DE=EF,
∴CE=DE,
∴E是CD的中点.
1.如图所示,已知∠C=∠D=90°,E是CD上的一点,AE,BE分别平分∠DAB,∠ABC.试说明:E是CD的中点.
F
(1)应用角平分线的性质时,“点在角平分线上”“点到角两边的距离”两个条件缺一不可,不能错用为角的平分线上的点到角两边上任意点的距离相等.
(2)由角平分线的性质不用说明三角形全等便可以直接得到线段相等,这是说明线段相等的一个简便方法.
应用角平分线的性质的两点注意
如图,已知∠AOB,如何作出它的平分线?
A
O
B
假设∠AOB 的平分线已作出,那么
(1)这条射线有什么特征
(2)如何确定这条射线上除端点之外的一个点 用三角尺、量角器、圆规等工具试一试.如果只用尺规呢 与同伴进行交流.
需要确定的点是角的对称轴上的点,因此应当从角两边进行“对称”的操作.
解:(1)这条射线到角两边的距离相等.
作法:
1.在OA和OB上分别截取OD,OE,使OD=OE.
D
E
C
例2 如图,已知∠AOB,请用尺规作∠AOB的平分线.
你能说明这样作的道理吗?
2.分别以点D和点E为圆心,以大于DE的长为半径作弧,两弧在∠AOB内相交于点C.
3.作射线OC.
射线OC就是∠AOB的平分线.
2.如图是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
A.△ABC的三条中线的交点
B.△ABC三边的中垂线的交点
C.△ABC三条高所在直线的交点
D.△ABC三条角平分线的交点
D
D
A
1.如图所示,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于点E,DB=5,BC=8,则DE的长为( )
A.3 B.4 C.5 D.6
2.如图所示,AB∥CD,O为∠BAC,∠ACD的平分线的交点, OE⊥AC于点E,且OE=3,则AB与CD之间的距离为( )
A.3 B.3.5 C.4 D.6
2
12
3.如图所示,在△ABC中,AD为∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F,△ABC的面积是14cm2,AB=9cm,AC=5cm,则DE的长是 cm.
4.如图所示,在△ABC中,∠C=90°,AD平分∠BAC,过点D作DE⊥AB于点E.若BC=9,BE=3,则△BDE的周长是 .
解:∵∠ACB=90°,
∴AC⊥BC.
又∵DE⊥AB,BE平分∠ABC,
∴CE=DE.
∵DE垂直平分AB,
∴AE=BE.
∵AE+CE=AC,
∴BE+DE=AC.
5.如图所示,在△ABC中,∠ACB=90°,BE平分∠ABC,交AC于点E,DE垂直平分AB,垂足为D.试说明:BE+DE=AC.
解:如图,点M即为所求.
6.如图所示,在△ABC中,P是AC上的一点,连接BP,求作一点M,使得点M到AB和AC两边的距离相等,并且到点B和点P的距离相等.(不写作法,保留作图痕迹)
角平分线上的点到这个角的两边的距离相等
角的对称性
角平分线的性质
应用注意:
一个点:角平分线上的点;
二距离:点到角两边的距离;
两相等:两条垂线段相等.
角平分线的性质
属于基本作图,必须熟练掌握
尺规作角平分线
角是轴对称图形,角平分线所在的直线是它的对称轴
5.2 简单的轴对称图形
第3课时 角平分线的性质
1. 通过操作、验证等方式,探究并掌握角平分线的性质定理;(重点)
2. 会用尺规作角平分线,能运用角的平分线性质解决简单的几何问题.(难点)
角是生活中常见的图形.角是轴对称图形吗
如果是,你能找出它的对称轴吗?
A
O
B
如图所示,将∠AOB对折,你发现了什么
角是 图形, 是它的对称轴.
轴对称
角平分线所在的直线
角的对称性
如图 5-19,OP是∠AOB的平分线,点C是OP上的任意一点.在∠AOB中画出以OP所在直线为对称轴的一组对应点D和D′连接CD和CD′.
(1)你认为线段CD和CD′之间有什么关系 说说你的理由.
解:(1)CD=CD′
理由:∵OP是∠AOB的平分线,
∴∠AOP=∠BOP.
∵点D和D′关于OP所在直线对称,
∴OD=OD′.
∵OC=OC,
∴△CDO≌△CD′O(SAS).
∴CD=CD′.
(2)特别地,当CD⊥OA时(如图5-20),CD′与OB有怎样的位置关系 为什么 此时,线段CD和CD′之间还有(1)中的关系吗
(2)CD′⊥OB.因为点D和点D′关于OP所在直线对称.
线段CD和CD′依旧相等.
由此你能得到什么结论
角平分线上的点到这个角的两边的距离相等.
角平分线的性质
应用格式:
∵OP是∠AOB的平分线,
∴PD=PE
PD⊥OA,PE⊥OB,
B
A
D
O
P
E
C
解:OB=OC.
理由如下:
∵点O在∠BAC的平分线上,OD⊥AC,OE⊥AB,
∴OE=OD,∠BEO=∠CDO=90°.
在△BEO和△CDO中,
∵∠BEO=∠CDO,OE=OD,∠EOB=∠DOC,
∴△BEO≌△CDO(ASA).
∴OB=OC.
例1 如图所示,点O在∠BAC的平分线上,OD⊥AC,OE⊥AB,垂足分别为D,E,DO,EO的延长线分别交AE,AD的延长线于点B,C,OB与OC相等吗?为什么?
解:过点E作EF⊥AB于点F.
∵∠C=∠D=90°,
∵AE,BE分别平分∠DAB,∠ABC,
∴CE=EF,DE=EF,
∴CE=DE,
∴E是CD的中点.
1.如图所示,已知∠C=∠D=90°,E是CD上的一点,AE,BE分别平分∠DAB,∠ABC.试说明:E是CD的中点.
F
(1)应用角平分线的性质时,“点在角平分线上”“点到角两边的距离”两个条件缺一不可,不能错用为角的平分线上的点到角两边上任意点的距离相等.
(2)由角平分线的性质不用说明三角形全等便可以直接得到线段相等,这是说明线段相等的一个简便方法.
应用角平分线的性质的两点注意
如图,已知∠AOB,如何作出它的平分线?
A
O
B
假设∠AOB 的平分线已作出,那么
(1)这条射线有什么特征
(2)如何确定这条射线上除端点之外的一个点 用三角尺、量角器、圆规等工具试一试.如果只用尺规呢 与同伴进行交流.
需要确定的点是角的对称轴上的点,因此应当从角两边进行“对称”的操作.
解:(1)这条射线到角两边的距离相等.
作法:
1.在OA和OB上分别截取OD,OE,使OD=OE.
D
E
C
例2 如图,已知∠AOB,请用尺规作∠AOB的平分线.
你能说明这样作的道理吗?
2.分别以点D和点E为圆心,以大于DE的长为半径作弧,两弧在∠AOB内相交于点C.
3.作射线OC.
射线OC就是∠AOB的平分线.
2.如图是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
A.△ABC的三条中线的交点
B.△ABC三边的中垂线的交点
C.△ABC三条高所在直线的交点
D.△ABC三条角平分线的交点
D
D
A
1.如图所示,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于点E,DB=5,BC=8,则DE的长为( )
A.3 B.4 C.5 D.6
2.如图所示,AB∥CD,O为∠BAC,∠ACD的平分线的交点, OE⊥AC于点E,且OE=3,则AB与CD之间的距离为( )
A.3 B.3.5 C.4 D.6
2
12
3.如图所示,在△ABC中,AD为∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F,△ABC的面积是14cm2,AB=9cm,AC=5cm,则DE的长是 cm.
4.如图所示,在△ABC中,∠C=90°,AD平分∠BAC,过点D作DE⊥AB于点E.若BC=9,BE=3,则△BDE的周长是 .
解:∵∠ACB=90°,
∴AC⊥BC.
又∵DE⊥AB,BE平分∠ABC,
∴CE=DE.
∵DE垂直平分AB,
∴AE=BE.
∵AE+CE=AC,
∴BE+DE=AC.
5.如图所示,在△ABC中,∠ACB=90°,BE平分∠ABC,交AC于点E,DE垂直平分AB,垂足为D.试说明:BE+DE=AC.
解:如图,点M即为所求.
6.如图所示,在△ABC中,P是AC上的一点,连接BP,求作一点M,使得点M到AB和AC两边的距离相等,并且到点B和点P的距离相等.(不写作法,保留作图痕迹)
角平分线上的点到这个角的两边的距离相等
角的对称性
角平分线的性质
应用注意:
一个点:角平分线上的点;
二距离:点到角两边的距离;
两相等:两条垂线段相等.
角平分线的性质
属于基本作图,必须熟练掌握
尺规作角平分线
角是轴对称图形,角平分线所在的直线是它的对称轴
同课章节目录
