6.3 用关系式表示变量之间的关系 课件(共26张PPT)
文档属性
| 名称 | 6.3 用关系式表示变量之间的关系 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-13 07:28:45 | ||
图片预览








文档简介
(共26张PPT)
6.3 用关系式表示变量之间的关系
1.根据具体情境,会用关系式表示某些变量之间的关系.(重点)
2.能根据关系式和自变量的值,求出对应的因变量的值.(难点)
游戏:数青蛙
一只青蛙一张嘴,两只眼睛四条腿;
两只青蛙两张嘴,四只眼睛八条腿;
三只青蛙三张嘴,六只眼睛十二条腿;
……
1.青蛙的眼睛数和只数有关系吗 能用数学式表达吗
2.青蛙的腿数和只数有关系吗 能用数学式表达吗
这个游戏你能继续玩下去吗
如图,△ABC底边BC上的高是6cm.
当三角形的顶点C沿底边所在直线向点
B运动时,三角形的面积发生了变化.
(1)在这个变化过程中,自变量、因变
量各是什么 当底边长减小时,三角形
的面积是如何变化的
自变量:三角形的底边长; 因变量:三角形的面积.
当底边长减小时,三角形的面积也减小.
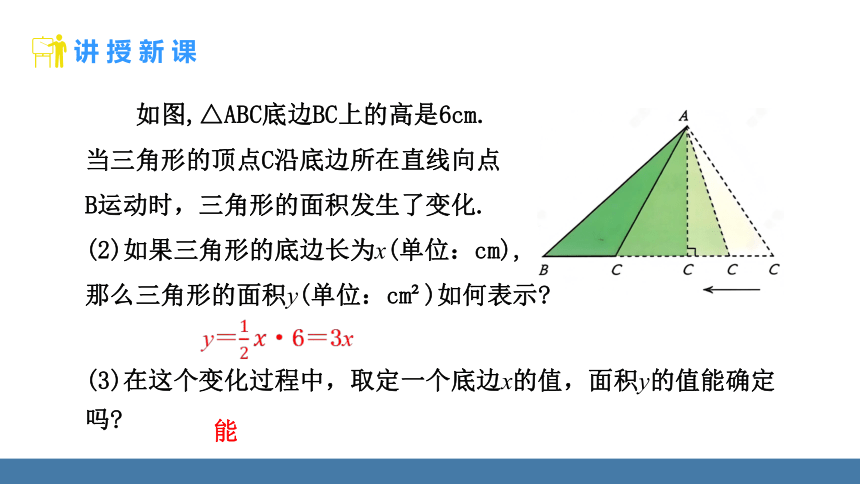
如图,△ABC底边BC上的高是6cm.
当三角形的顶点C沿底边所在直线向点
B运动时,三角形的面积发生了变化.
(2)如果三角形的底边长为x(单位:cm),
那么三角形的面积y(单位:cm )如何表示
(3)在这个变化过程中,取定一个底边x的值,面积y的值能确定吗
y=·6=3x
能
y=3x表示了上图中△ABC底边长x和面积y之间的关系,它是变量随x变化的关系式.
关系式是我们表示变量之间关系的另一种方法,利用关系式(如y=3x),我们可以根据任何一个自变量值求出相应的因变量的值.
如图,圆锥的高是 4 cm,当圆锥的底面半径由小到大变化时,圆锥的体积也随之发生了变化.
(1)在这个变化过程中,自变量、因变量各是什么 底面半径增大时,圆锥的体积是如何变化的
圆锥的底面半径的长度是自变量,圆锥的体积是因变量.
底面半径增大时,圆锥的体积也随之增大.
如图,圆锥的高是4 cm,当圆锥的底面
半径由小到大变化时,圆锥的体积也随之
发生了变化.
(2)如果圆锥的底面半径为r(单位:cm),那
么圆锥的体积V(单位:cm )如何表示
(3)在这个变化过程中,取定一个底面半径r的值,体积V的值能确定吗
V=πr2
能
例1 如图,在一块矩形钢板上,截下两个完全相同的半圆,设阴影部分的面积为 S(cm2),半圆的直径为 a cm.
(1)指出其中的常量与变量;
(2)求S与a的关系式,并求a=10 cm时阴影部分的面积(结果保留π).
解:(1)∵a的值能发生变化,S的值随之发生变化,所以π是常量,S,a是变量.
解:(2)S=长方形的面积-2个半圆的面积
=60×20-2×π·()
=1200-
∴S与a的关系式为S=1200-
当a=10 cm时,
S=1200-
=(1200-25π)cm .
例1 (2)求S与a的关系式,并求a=10cm时阴影部分的面积(结果保留π).
你知道什么是“低碳生活”吗 “低碳生活”是指人们尽量减少所耗能量,从而降低碳(特别是二氧化碳)的排放量的一种生活方式.
一些常见的二氧化碳排放量计算公式如下表所示:
二氧化碳排放量/kg 计算公式
家居用电 用电量(单位:kW ·h)×0.785
开私家车(燃油车) 耗油量(单位:L)×2.7
家用天然气 用气量(单位:m )×0.19
家用自来水 用水量(单位:m )×0.91
(1)你能用字母表示家居用电的二氧化碳排放量的公式吗 其中的字母表示什么
二氧化碳排放量/kg 计算公式
家居用电 用电量(单位:kW ·h)×0.785
开私家车(燃油车) 耗油量(单位:L)×2.7
家用天然气 用气量(单位:m )×0.19
家用自来水 用水量(单位:m )×0.91
家居用电的二氧化碳排放量可以用关系式表示为y=0.785x,
其中字母表示二氧化碳排放量和用电量.
(2)随着耗电量的增加,二氧化碳排放量是如何变化的
二氧化碳排放量/kg 计算公式
家居用电 用电量(单位:kW ·h)×0.785
开私家车(燃油车) 耗油量(单位:L)×2.7
家用天然气 用气量(单位:m )×0.19
家用自来水 用水量(单位:m )×0.91
在上述关系式中,耗电量每增加1kW·h,二氧化碳排放量增加0.785kg.
(3)当耗电量为100 kW·h时,二氧化碳排放量是多少
二氧化碳排放量/kg 计算公式
家居用电 用电量(单位:kW ·h)×0.785
开私家车(燃油车) 耗油量(单位:L)×2.7
家用天然气 用气量(单位:m )×0.19
家用自来水 用水量(单位:m )×0.91
当耗电量从1kW·h增加到100kW·h时,二氧化碳排放量从0.785kg增加到78.5kg.
(4)小明家本月大约用电110kW·h、耗油75L、用天然气20 m 、用自来水5m ,请你计算小明家这几项的二氧化碳排放量总和.
二氧化碳排放量/kg 计算公式
家居用电 用电量(单位:kW ·h)×0.785
开私家车(燃油车) 耗油量(单位:L)×2.7
家用天然气 用气量(单位:m )×0.19
家用自来水 用水量(单位:m )×0.91
y=110×0.785+20×0.19+5×0.91+75×2.7
=297.2kg
例2 变量x与y之间的关系式是y=x -3,当自变量x=2时,因变量y的值是( )
A.-2 B.-1 C.1 D.2
【解析】将x=2代入y=x -3,得y=22-3=1.
C
变量的求值方法:
(1)已知自变量,利用关系式求因变量的值,实际上就是求代数式的值;
(2)利用关系式求自变量的值,实际上就是求方程的解.
注意:在一些实际问题中,自变量只能取某个范围内的值.
议一议:列表格与列关系式表示变量之间的关系各有什么特点
通过列表格,可以较直观地表示因变量随自变量变化而变化的情况.
通过关系式,可以根据一个自变量的值求出相应的因变量的值.
1.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂重物的质量x(kg)有下表所示的关系,那么在弹性限度内,弹簧总长y(cm)与所挂重物的质量x(kg)之间的关系式为( )
A.y=x+12 B.y=0.5x+12
C.y=0.5x+10 D.y=x+10.5
B
x(kg) 0 1 2 3 4 5 6 …
y(cm) 12 12.5 13 13.5 14 14.5 15 …
2.出生1~6个月的婴儿生长发育得非常快,他们的体重y(g)与月龄x(月)间的关系可以用y=a+700x来表示,其中a是婴儿出生时的体重.若一个婴儿出生时的体重是3000 g,则这个婴儿第4个月的体重为( )
A.6 000g B.5 800g
C.5 000g D.5 100g
B
3.如图所示,梯形的上底长是5 cm,下底长是13 cm.当梯形的高由大变小时,梯形的面积也随之发生变化梯形的高梯形的面积:
(1)在这个变化过程中,自变量是 __,因变量是 _.
(2)梯形的面积y(cm )与高x(cm)之间的关系式 ;
(3)当梯形的高由10 cm变化到
1 cm时,梯形的面积由 cm
变化到_ _cm .
5
13
x
梯形的高
梯形的面积
y=9x(x>0)
90
9
4.如图,用一段长为60 m的篱笆围成一个一边靠墙(墙的长度不限)的长方形菜园ABCD,设与墙平行的篱笆AB的长为 x m,菜园的面积为 y m .
(1)试写出y与x之间的关系式(不必写出x的取值范围);
(2)当AB的长为10 m,20 m时,菜园的面积各是多少
解:(1)根据题意,得AD的长为(30-0.5x)m,
则y=x(30-0.5x),
即y=-0.5x +30x
(2)当x=10时,y=250;
当x=20时,y=400.
故当AB的长为10 m,20 m时,
菜园的面积分别是250 m2,400 m2.
5.某剧院的观众席的座位按扇形排列,已知座位数与排数之间的关系如下表:
排数(x) 1 2 3 4 …
座位数(y) 50 53 56 59 …
(1)此剧院第三排有多少座位
(2)按照上表所示的规律,当排数x每增加1时,座位数y如何变化
(3)写出座位数y与排数x之间的关系式;
(4)按照上表所示的规律,某一排可能有90个座位吗 说说你的理由.
解:(1)此剧院第三排有56个座位.
(2)当排数x每增加1时,座位数y增加3.
(3)由题意可得y=50+3(x-1)=3x+47,
即座位数y与排数x之间的关系式是y=3x+47.
(4)不可能.
理由:当y=90时,90=3x+47,解得x=,
此方程无整数解,故某一排不可能有90个座位.
关系式法
用关系式表示的变量间关系
关系式是用含自变量的代数式表示因变量的等式.
注意:关系式是一个等式,通常把因变量写在等号的左边,含有自变量的代数式写在等号的右边.
根据关系式
求变量的值
(1)已知自变量,利用关系式求因变量的值,实际上就是求代数式的值;
(2)利用关系式求自变量的值,实际上就是求方程的解.
6.3 用关系式表示变量之间的关系
1.根据具体情境,会用关系式表示某些变量之间的关系.(重点)
2.能根据关系式和自变量的值,求出对应的因变量的值.(难点)
游戏:数青蛙
一只青蛙一张嘴,两只眼睛四条腿;
两只青蛙两张嘴,四只眼睛八条腿;
三只青蛙三张嘴,六只眼睛十二条腿;
……
1.青蛙的眼睛数和只数有关系吗 能用数学式表达吗
2.青蛙的腿数和只数有关系吗 能用数学式表达吗
这个游戏你能继续玩下去吗
如图,△ABC底边BC上的高是6cm.
当三角形的顶点C沿底边所在直线向点
B运动时,三角形的面积发生了变化.
(1)在这个变化过程中,自变量、因变
量各是什么 当底边长减小时,三角形
的面积是如何变化的
自变量:三角形的底边长; 因变量:三角形的面积.
当底边长减小时,三角形的面积也减小.
如图,△ABC底边BC上的高是6cm.
当三角形的顶点C沿底边所在直线向点
B运动时,三角形的面积发生了变化.
(2)如果三角形的底边长为x(单位:cm),
那么三角形的面积y(单位:cm )如何表示
(3)在这个变化过程中,取定一个底边x的值,面积y的值能确定吗
y=·6=3x
能
y=3x表示了上图中△ABC底边长x和面积y之间的关系,它是变量随x变化的关系式.
关系式是我们表示变量之间关系的另一种方法,利用关系式(如y=3x),我们可以根据任何一个自变量值求出相应的因变量的值.
如图,圆锥的高是 4 cm,当圆锥的底面半径由小到大变化时,圆锥的体积也随之发生了变化.
(1)在这个变化过程中,自变量、因变量各是什么 底面半径增大时,圆锥的体积是如何变化的
圆锥的底面半径的长度是自变量,圆锥的体积是因变量.
底面半径增大时,圆锥的体积也随之增大.
如图,圆锥的高是4 cm,当圆锥的底面
半径由小到大变化时,圆锥的体积也随之
发生了变化.
(2)如果圆锥的底面半径为r(单位:cm),那
么圆锥的体积V(单位:cm )如何表示
(3)在这个变化过程中,取定一个底面半径r的值,体积V的值能确定吗
V=πr2
能
例1 如图,在一块矩形钢板上,截下两个完全相同的半圆,设阴影部分的面积为 S(cm2),半圆的直径为 a cm.
(1)指出其中的常量与变量;
(2)求S与a的关系式,并求a=10 cm时阴影部分的面积(结果保留π).
解:(1)∵a的值能发生变化,S的值随之发生变化,所以π是常量,S,a是变量.
解:(2)S=长方形的面积-2个半圆的面积
=60×20-2×π·()
=1200-
∴S与a的关系式为S=1200-
当a=10 cm时,
S=1200-
=(1200-25π)cm .
例1 (2)求S与a的关系式,并求a=10cm时阴影部分的面积(结果保留π).
你知道什么是“低碳生活”吗 “低碳生活”是指人们尽量减少所耗能量,从而降低碳(特别是二氧化碳)的排放量的一种生活方式.
一些常见的二氧化碳排放量计算公式如下表所示:
二氧化碳排放量/kg 计算公式
家居用电 用电量(单位:kW ·h)×0.785
开私家车(燃油车) 耗油量(单位:L)×2.7
家用天然气 用气量(单位:m )×0.19
家用自来水 用水量(单位:m )×0.91
(1)你能用字母表示家居用电的二氧化碳排放量的公式吗 其中的字母表示什么
二氧化碳排放量/kg 计算公式
家居用电 用电量(单位:kW ·h)×0.785
开私家车(燃油车) 耗油量(单位:L)×2.7
家用天然气 用气量(单位:m )×0.19
家用自来水 用水量(单位:m )×0.91
家居用电的二氧化碳排放量可以用关系式表示为y=0.785x,
其中字母表示二氧化碳排放量和用电量.
(2)随着耗电量的增加,二氧化碳排放量是如何变化的
二氧化碳排放量/kg 计算公式
家居用电 用电量(单位:kW ·h)×0.785
开私家车(燃油车) 耗油量(单位:L)×2.7
家用天然气 用气量(单位:m )×0.19
家用自来水 用水量(单位:m )×0.91
在上述关系式中,耗电量每增加1kW·h,二氧化碳排放量增加0.785kg.
(3)当耗电量为100 kW·h时,二氧化碳排放量是多少
二氧化碳排放量/kg 计算公式
家居用电 用电量(单位:kW ·h)×0.785
开私家车(燃油车) 耗油量(单位:L)×2.7
家用天然气 用气量(单位:m )×0.19
家用自来水 用水量(单位:m )×0.91
当耗电量从1kW·h增加到100kW·h时,二氧化碳排放量从0.785kg增加到78.5kg.
(4)小明家本月大约用电110kW·h、耗油75L、用天然气20 m 、用自来水5m ,请你计算小明家这几项的二氧化碳排放量总和.
二氧化碳排放量/kg 计算公式
家居用电 用电量(单位:kW ·h)×0.785
开私家车(燃油车) 耗油量(单位:L)×2.7
家用天然气 用气量(单位:m )×0.19
家用自来水 用水量(单位:m )×0.91
y=110×0.785+20×0.19+5×0.91+75×2.7
=297.2kg
例2 变量x与y之间的关系式是y=x -3,当自变量x=2时,因变量y的值是( )
A.-2 B.-1 C.1 D.2
【解析】将x=2代入y=x -3,得y=22-3=1.
C
变量的求值方法:
(1)已知自变量,利用关系式求因变量的值,实际上就是求代数式的值;
(2)利用关系式求自变量的值,实际上就是求方程的解.
注意:在一些实际问题中,自变量只能取某个范围内的值.
议一议:列表格与列关系式表示变量之间的关系各有什么特点
通过列表格,可以较直观地表示因变量随自变量变化而变化的情况.
通过关系式,可以根据一个自变量的值求出相应的因变量的值.
1.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂重物的质量x(kg)有下表所示的关系,那么在弹性限度内,弹簧总长y(cm)与所挂重物的质量x(kg)之间的关系式为( )
A.y=x+12 B.y=0.5x+12
C.y=0.5x+10 D.y=x+10.5
B
x(kg) 0 1 2 3 4 5 6 …
y(cm) 12 12.5 13 13.5 14 14.5 15 …
2.出生1~6个月的婴儿生长发育得非常快,他们的体重y(g)与月龄x(月)间的关系可以用y=a+700x来表示,其中a是婴儿出生时的体重.若一个婴儿出生时的体重是3000 g,则这个婴儿第4个月的体重为( )
A.6 000g B.5 800g
C.5 000g D.5 100g
B
3.如图所示,梯形的上底长是5 cm,下底长是13 cm.当梯形的高由大变小时,梯形的面积也随之发生变化梯形的高梯形的面积:
(1)在这个变化过程中,自变量是 __,因变量是 _.
(2)梯形的面积y(cm )与高x(cm)之间的关系式 ;
(3)当梯形的高由10 cm变化到
1 cm时,梯形的面积由 cm
变化到_ _cm .
5
13
x
梯形的高
梯形的面积
y=9x(x>0)
90
9
4.如图,用一段长为60 m的篱笆围成一个一边靠墙(墙的长度不限)的长方形菜园ABCD,设与墙平行的篱笆AB的长为 x m,菜园的面积为 y m .
(1)试写出y与x之间的关系式(不必写出x的取值范围);
(2)当AB的长为10 m,20 m时,菜园的面积各是多少
解:(1)根据题意,得AD的长为(30-0.5x)m,
则y=x(30-0.5x),
即y=-0.5x +30x
(2)当x=10时,y=250;
当x=20时,y=400.
故当AB的长为10 m,20 m时,
菜园的面积分别是250 m2,400 m2.
5.某剧院的观众席的座位按扇形排列,已知座位数与排数之间的关系如下表:
排数(x) 1 2 3 4 …
座位数(y) 50 53 56 59 …
(1)此剧院第三排有多少座位
(2)按照上表所示的规律,当排数x每增加1时,座位数y如何变化
(3)写出座位数y与排数x之间的关系式;
(4)按照上表所示的规律,某一排可能有90个座位吗 说说你的理由.
解:(1)此剧院第三排有56个座位.
(2)当排数x每增加1时,座位数y增加3.
(3)由题意可得y=50+3(x-1)=3x+47,
即座位数y与排数x之间的关系式是y=3x+47.
(4)不可能.
理由:当y=90时,90=3x+47,解得x=,
此方程无整数解,故某一排不可能有90个座位.
关系式法
用关系式表示的变量间关系
关系式是用含自变量的代数式表示因变量的等式.
注意:关系式是一个等式,通常把因变量写在等号的左边,含有自变量的代数式写在等号的右边.
根据关系式
求变量的值
(1)已知自变量,利用关系式求因变量的值,实际上就是求代数式的值;
(2)利用关系式求自变量的值,实际上就是求方程的解.
同课章节目录
