6.4 用图象表示变量之间的关系 第2课时 课件(共18张PPT)
文档属性
| 名称 | 6.4 用图象表示变量之间的关系 第2课时 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-13 07:28:18 | ||
图片预览



文档简介
(共18张PPT)
6.4 用图象表示变量之间的关系
第2课时 折线型图象
1.能从图象分析变量之间的关系,加深对图象表示的理解;
2.能对实际情境中所蕴涵的变量之间的关系借助图象表示;
3.进一步体会数学与现实生活的密切联系,并在学习新知识的过程中培养学生团结协作的精神.
1.表示变量之间的关系有几种方法
2.他们的优点是什么
列表法:数值清晰,一目了然.
关系式法:显示推理,便于计算.
图象法:形象直观,探索趋势.
列表法、关系式法、图象法
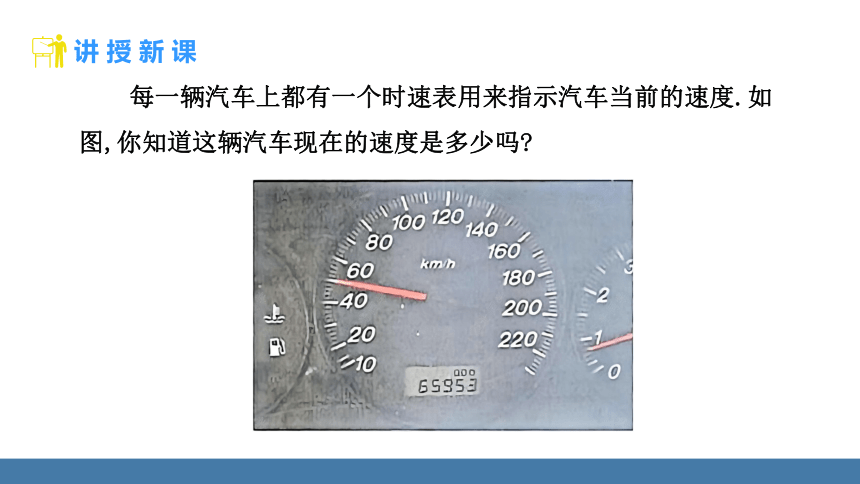
每一辆汽车上都有一个时速表用来指示汽车当前的速度.如图,你知道这辆汽车现在的速度是多少吗
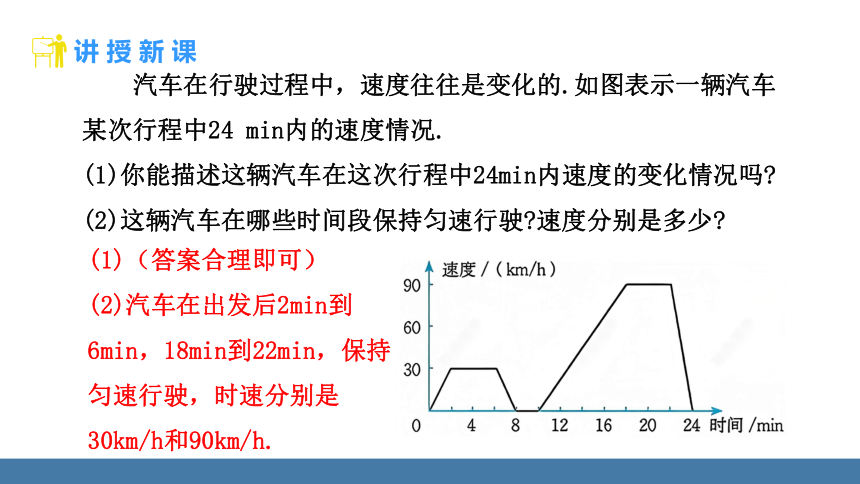
汽车在行驶过程中,速度往往是变化的.如图表示一辆汽车某次行程中24 min内的速度情况.
(1)你能描述这辆汽车在这次行程中24min内速度的变化情况吗
(2)这辆汽车在哪些时间段保持匀速行驶 速度分别是多少
(1)(答案合理即可)
(2)汽车在出发后2min到6min,18min到22min,保持匀速行驶,时速分别是30km/h和90km/h.
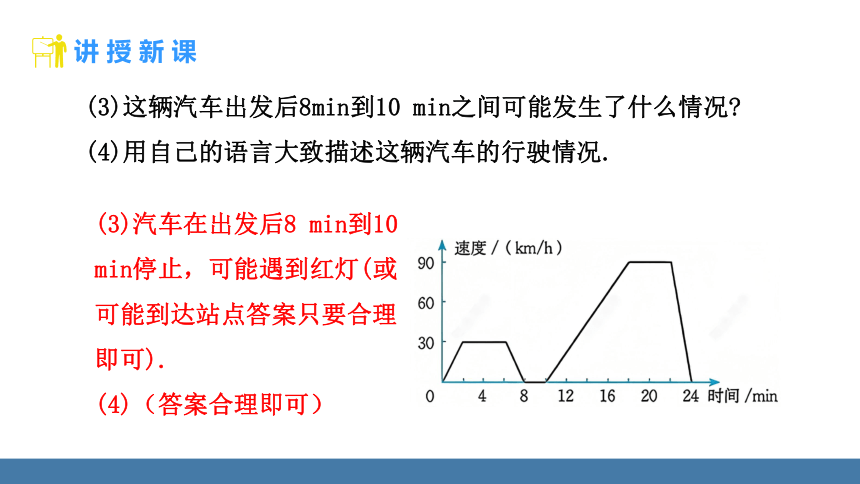
(3)这辆汽车出发后8min到10 min之间可能发生了什么情况
(4)用自己的语言大致描述这辆汽车的行驶情况.
(3)汽车在出发后8 min到10 min停止,可能遇到红灯(或可能到达站点答案只要合理即可).
(4)(答案合理即可)
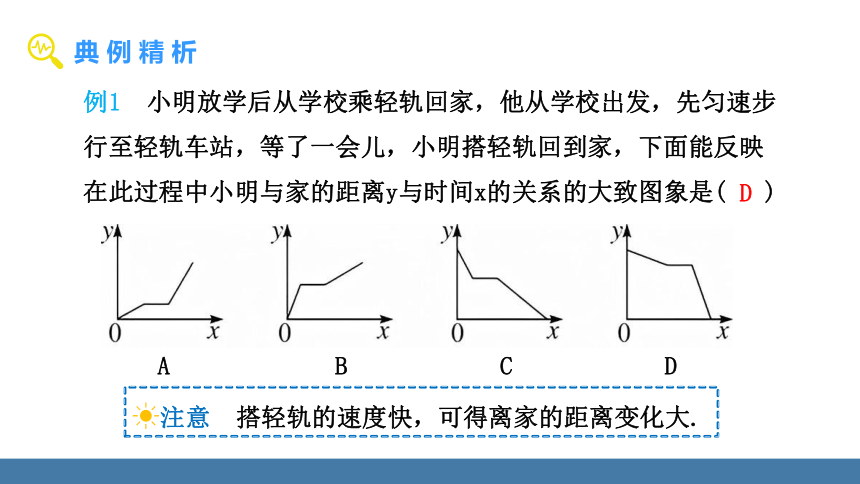
例1 小明放学后从学校乘轻轨回家,他从学校出发,先匀速步行至轻轨车站,等了一会儿,小明搭轻轨回到家,下面能反映在此过程中小明与家的距离y与时间x的关系的大致图象是( )
D
A B C D
注意 搭轻轨的速度快,可得离家的距离变化大.
在前面的情境中,假设这辆汽车出发后8 min到12 min静止不动,然后用6 min加速到90 km/h,再用6min减速到静止.你能在下图中画图大致反映这辆汽车的速度随着时间的变化而变化的情况吗
三种方法表示变量间的关系,各自有什么优缺点呢
优点 缺 点
表格法 直观反映两个变量部分数值的对应关系及变化趋势 变量的取值个数有限,
估计时比较粗略
关系式 准确反映两个变量间的数量关系;已知一个变量的值,可以求出另一个变量的值 变量间的对应关系不太直观
图象法 能够直观地看出因变量随自变量变
化的情况 变量间的对应关系不
准确
例2 某年初,我国西南部分省市遭遇了严重干旱.某水库的蓄水量随着时间的增加而减小,干旱持续时间t(天)与蓄水量V(万立方米)的变化情况如图,根据图象回答问题:
(1)这个图象反映了哪两个变量之间的关系
图象反映了干旱持续时间与水库蓄水量之间的关系.
(2)根据图象填表:
干旱持续时间t/天 0 10 20 30 40 50 60
蓄水量V/万立方米
(3)当t 取0至60天之间的任一值时,对应几个V值
1200
1000
800
600
400
200
0
(3)当t 取0至60天之间的任一值时,对应着一个V值.
(4)写出V和t之间的关系式
(4)根据图象可知,该水库初始蓄水量为1200万立方米,干旱每持续10天,蓄水量相应减少200万立方米,所以V和t之间
200的关系式为
V=1200-t=-20t+1200(0≤t≤60).
1.李明骑车上学,一开始以某一速度行进,途中车子发生故障,只好停下来修车,车修好后,因怕耽误上学时间,于是加快马加鞭车速,在下图中给出的示意图中(s为距离,t为时间)符合以上情况的是( )
D
2.用均匀的速度向一个容器注水,最后把容器注满,在注水过程中,水面高度随时间t的变化规律如图所示(图中OAB为折线),这个容器的形状是图中( )
C
3.下列各情境分别可以用哪幅图来近似地刻画
(1)一杯越来越凉的水(水温与时间的关系);
(2)一面冉冉上升的旗子(高度与时间的关系);
(3)足球守门员大脚开出去的球(高度与时间的关系);
(4)匀速行驶的汽车(速度与时间的关系).
C
D
A
B
4.甲骑自行车、乙骑摩托车沿相同路线由A地到B地,行驶过程中路程与时间关系的图象如图所示,根据图象解答下列问题:
(1)谁先出发 先出发多少时间 谁先到达终点 先到多少时间
解:由图象可知:
(1)甲先出发;先出发10分钟;
乙先到达终点;先到5分钟;
(2)分别求出甲、乙两人的行驶速度;
(3)在什么时间段内,两人均行驶在途
中 (不包括起点和终点)
在甲出发后10分钟到25分钟这段时间内,两人都行驶在途中.
甲的速度为6÷30=0.2(公里/分钟),
乙的速度为6÷15=0.4(公里/分钟);
表示方法
两个变量之间关系
表格法、关系式、图象法
图象法的优越性
图象法能直观反映变量间的整体变化情况及变化规律
6.4 用图象表示变量之间的关系
第2课时 折线型图象
1.能从图象分析变量之间的关系,加深对图象表示的理解;
2.能对实际情境中所蕴涵的变量之间的关系借助图象表示;
3.进一步体会数学与现实生活的密切联系,并在学习新知识的过程中培养学生团结协作的精神.
1.表示变量之间的关系有几种方法
2.他们的优点是什么
列表法:数值清晰,一目了然.
关系式法:显示推理,便于计算.
图象法:形象直观,探索趋势.
列表法、关系式法、图象法
每一辆汽车上都有一个时速表用来指示汽车当前的速度.如图,你知道这辆汽车现在的速度是多少吗
汽车在行驶过程中,速度往往是变化的.如图表示一辆汽车某次行程中24 min内的速度情况.
(1)你能描述这辆汽车在这次行程中24min内速度的变化情况吗
(2)这辆汽车在哪些时间段保持匀速行驶 速度分别是多少
(1)(答案合理即可)
(2)汽车在出发后2min到6min,18min到22min,保持匀速行驶,时速分别是30km/h和90km/h.
(3)这辆汽车出发后8min到10 min之间可能发生了什么情况
(4)用自己的语言大致描述这辆汽车的行驶情况.
(3)汽车在出发后8 min到10 min停止,可能遇到红灯(或可能到达站点答案只要合理即可).
(4)(答案合理即可)
例1 小明放学后从学校乘轻轨回家,他从学校出发,先匀速步行至轻轨车站,等了一会儿,小明搭轻轨回到家,下面能反映在此过程中小明与家的距离y与时间x的关系的大致图象是( )
D
A B C D
注意 搭轻轨的速度快,可得离家的距离变化大.
在前面的情境中,假设这辆汽车出发后8 min到12 min静止不动,然后用6 min加速到90 km/h,再用6min减速到静止.你能在下图中画图大致反映这辆汽车的速度随着时间的变化而变化的情况吗
三种方法表示变量间的关系,各自有什么优缺点呢
优点 缺 点
表格法 直观反映两个变量部分数值的对应关系及变化趋势 变量的取值个数有限,
估计时比较粗略
关系式 准确反映两个变量间的数量关系;已知一个变量的值,可以求出另一个变量的值 变量间的对应关系不太直观
图象法 能够直观地看出因变量随自变量变
化的情况 变量间的对应关系不
准确
例2 某年初,我国西南部分省市遭遇了严重干旱.某水库的蓄水量随着时间的增加而减小,干旱持续时间t(天)与蓄水量V(万立方米)的变化情况如图,根据图象回答问题:
(1)这个图象反映了哪两个变量之间的关系
图象反映了干旱持续时间与水库蓄水量之间的关系.
(2)根据图象填表:
干旱持续时间t/天 0 10 20 30 40 50 60
蓄水量V/万立方米
(3)当t 取0至60天之间的任一值时,对应几个V值
1200
1000
800
600
400
200
0
(3)当t 取0至60天之间的任一值时,对应着一个V值.
(4)写出V和t之间的关系式
(4)根据图象可知,该水库初始蓄水量为1200万立方米,干旱每持续10天,蓄水量相应减少200万立方米,所以V和t之间
200的关系式为
V=1200-t=-20t+1200(0≤t≤60).
1.李明骑车上学,一开始以某一速度行进,途中车子发生故障,只好停下来修车,车修好后,因怕耽误上学时间,于是加快马加鞭车速,在下图中给出的示意图中(s为距离,t为时间)符合以上情况的是( )
D
2.用均匀的速度向一个容器注水,最后把容器注满,在注水过程中,水面高度随时间t的变化规律如图所示(图中OAB为折线),这个容器的形状是图中( )
C
3.下列各情境分别可以用哪幅图来近似地刻画
(1)一杯越来越凉的水(水温与时间的关系);
(2)一面冉冉上升的旗子(高度与时间的关系);
(3)足球守门员大脚开出去的球(高度与时间的关系);
(4)匀速行驶的汽车(速度与时间的关系).
C
D
A
B
4.甲骑自行车、乙骑摩托车沿相同路线由A地到B地,行驶过程中路程与时间关系的图象如图所示,根据图象解答下列问题:
(1)谁先出发 先出发多少时间 谁先到达终点 先到多少时间
解:由图象可知:
(1)甲先出发;先出发10分钟;
乙先到达终点;先到5分钟;
(2)分别求出甲、乙两人的行驶速度;
(3)在什么时间段内,两人均行驶在途
中 (不包括起点和终点)
在甲出发后10分钟到25分钟这段时间内,两人都行驶在途中.
甲的速度为6÷30=0.2(公里/分钟),
乙的速度为6÷15=0.4(公里/分钟);
表示方法
两个变量之间关系
表格法、关系式、图象法
图象法的优越性
图象法能直观反映变量间的整体变化情况及变化规律
同课章节目录
