8.1与三角形有关的边和角(含答案)
文档属性
| 名称 | 8.1与三角形有关的边和角(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 366.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-12 17:27:01 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
8.1与三角形有关的边和角(培优)
一、单选题
1.以下列各组线段为边,能组成三角形的是( )
A.3cm,3cm,6cm B.12cm,4cm,7cm
C.5cm,6cm,2cm D.2cm,7cm,4cm
2.下列语句正确的是( )
A.三角形的三条高都在三角形内部
B.三角形不一定具有稳定性
C.三角形的三条中线交于一点
D.三角形的角平分线可能在三角形的内部或外部
3.一个三角形的两边长分别为,,则这个三角形的第三条边的长可能是( )
A. B. C. D.
4.如图图形中,作的边上的高,正确的是( )
A. B.
C. D.
5.把一根长12厘米的铁丝按下面所标长度剪开,剪成的三段首尾顺次相接可以围成三角形的是( )
A. B.
C. D.
6.如图,在△ABC中,D,E分别为BC,AD的中点,且S△ABC=4,则S阴影为( )
A.2 B.1 C. D.
7.如图,已知直线,,,则等于( )
A. B. C. D.
8.如图,AD是△ABC的角平分线,点O在AD上,且OE⊥BC于点E,∠BAC=60°,∠C=80°,则∠EOD的度数为( )
A.20° B.30° C.10° D.15°
9.下列说法正确的是( )
A.一个钝角三角形一定不是等腰三角形,也不是等边三角形
B.一个等腰三角形一定是锐角三角形,或直角三角形
C.一个直角三角形一定不是等腰三角形,也不是等边三角形
D.一个等边三角形一定不是钝角三角形,也不是直角三角形
10.小明把一副直角三角尺按如图所示的方式摆放在一起,则等于( )
A. B. C. D.
二、填空题
11.如下图,的面积为1,分别倍长(延长一倍),,得到,再分别倍长,,得到.…按此规律,倍长2020次后得到的的面积为 .
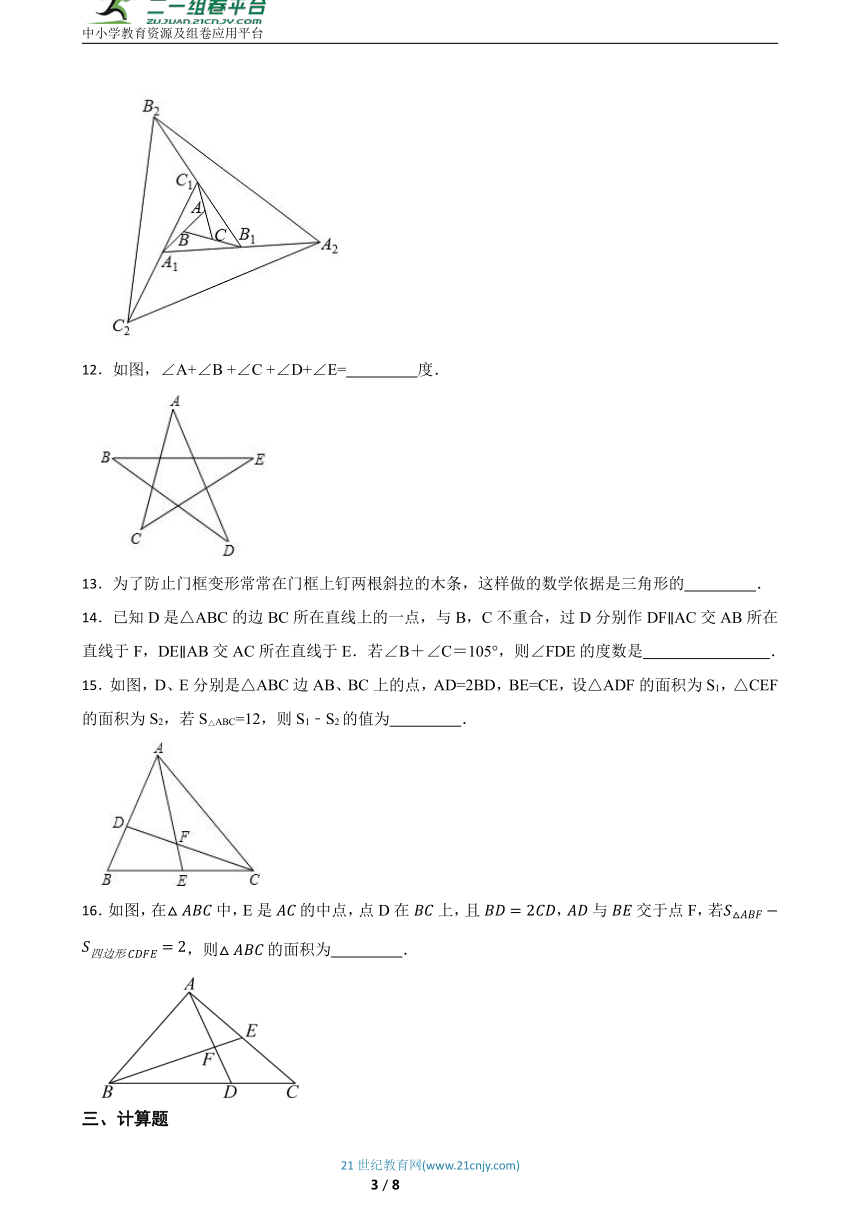
12.如图,∠A+∠B +∠C +∠D+∠E= 度.
13.为了防止门框变形常常在门框上钉两根斜拉的木条,这样做的数学依据是三角形的 .
14.已知D是△ABC的边BC所在直线上的一点,与B,C不重合,过D分别作DFAC交AB所在直线于F,DEAB交AC所在直线于E.若∠B+∠C=105°,则∠FDE的度数是 .
15.如图,D、E分别是△ABC边AB、BC上的点,AD=2BD,BE=CE,设△ADF的面积为S1,△CEF的面积为S2,若S△ABC=12,则S1﹣S2的值为 .
16.如图,在中,E是的中点,点D在上,且,与交于点F,若,则的面积为 .
三、计算题
17.已知a,b,c是三角形的三边长,化简:.
18.如图,在△ABC中,∠BAC=50°,∠B=60°,AE⊥BC于点E,CD平分∠ACB且分别与AB、AE交于点D、F,求∠AFC的度数.
19.计算题.
(1)已知一个多边形的内角和是1260°,求这个多边形的边数.
(2)用一条长为18cm的细绳围成一个等腰三角形,若有一边长等于4cm,求另外两边长.
四、解答题
20.在中,,,,求的度数.
21.在中,,,求的度数.
22.新定义:在中,若存在最大内角是最小内角度数的n倍(n为大于1的正整数),则称为“n倍角三角形”. 例如,在中,若∠,则,因为最大,最小,且,所以为“3倍角三角形”.
(1)在中,若,则△DEF为“_______倍角三角形”.
(2)如图,在中,的角平分线相交于点D,若为“3倍角三角形”,请求出的度数.
23. 如图,在中.
(1)的角平分线相交于点,求的度数;
(2)的三等分线分别相交于点,求的度数;
(3)的等分线分别相交于点,则 (结果用含的式子表示), (,为整数,结果用含和的式子表示)
答案解析部分
1.【答案】C
【知识点】三角形三边关系
2.【答案】C
【知识点】三角形的角平分线、中线和高;三角形的稳定性
3.【答案】B
【知识点】三角形三边关系
4.【答案】A
【知识点】三角形的角平分线、中线和高
5.【答案】D
【知识点】三角形三边关系
6.【答案】B
【知识点】三角形的角平分线、中线和高
7.【答案】B
【知识点】平行线的性质;三角形的外角性质
8.【答案】A
【知识点】三角形内角和定理;三角形的外角性质
9.【答案】D
【知识点】三角形三边关系
10.【答案】C
【知识点】三角形内角和定理;三角形的外角性质
11.【答案】
【知识点】三角形的角平分线、中线和高
12.【答案】180
【知识点】三角形内角和定理;三角形的外角性质
13.【答案】稳定性
【知识点】三角形的稳定性
14.【答案】75°或105°
【知识点】平行线的性质;三角形内角和定理
15.【答案】2
【知识点】三角形的面积
16.【答案】12
【知识点】三角形的角平分线、中线和高;三角形的面积
17.【答案】
【知识点】整式的加减运算;三角形三边关系;化简含绝对值有理数
18.【答案】解:∵AE⊥BC,∴∠AEB=90°.
∵∠B=60°,
∴∠BAE=90°﹣60°=30°.
∴∠CAE=50°﹣30°=20°
∵∠BAC+∠B+∠ACB=180°,
∴∠ACB=180°﹣∠BAC﹣∠B=70°.
又∵CD平分∠ACB,
∴∠ACD= ∠ACB=35°.
∴∠AFC=180°﹣35°﹣20°=125°.
【知识点】三角形内角和定理;三角形的外角性质;角平分线的概念
19.【答案】(1)9;(2)7 cm ,7 cm.
【知识点】三角形三边关系
20.【答案】
【知识点】三角形的外角性质
21.【答案】
【知识点】三角形内角和定理
22.【答案】(1)2
(2)
【知识点】三角形内角和定理
23.【答案】(1)解:∵ ∠ABC,∠ACB的角平分线相交于点P,
∴ ∠PBC=∠ABC,∠PCB=∠ACB,
∵ ∠A=60°,
∴ ∠BPC=180°-(∠PBC+∠PCB)=180°-(∠ABC+∠ACB)=180°-(180°-∠A)=90°+∠A=120°.
(2)解:∵ ∠ABC,∠ACB的三等分线分别相交于点P1,P2,
∴ ∠P1BC=∠ABC,∠P1CB=∠ACB,
∵ ∠A=60°,
∴ ∠BP1C=180°-(∠P1BC+∠P1CB)=180°-(∠ABC+∠ACB)=180°-(180°-∠A)=120°+∠A=140°,
∵ ∠ABC,∠ACB的三等分线分别相交于点P1,P2,
∴ ∠P2BC=∠ABC,∠P2CB=∠ACB,
∵ ∠A=60°,
∴ ∠BP2C=180°-(∠P2BC+∠P2CB)=180°-(∠ABC+∠ACB)=180°-(180°-∠A)=60°+∠A=100°.
(3);
【知识点】三角形内角和定理;角平分线的概念
21世纪教育网(www.21cnjy.com)
8 / 8
8.1与三角形有关的边和角(培优)
一、单选题
1.以下列各组线段为边,能组成三角形的是( )
A.3cm,3cm,6cm B.12cm,4cm,7cm
C.5cm,6cm,2cm D.2cm,7cm,4cm
2.下列语句正确的是( )
A.三角形的三条高都在三角形内部
B.三角形不一定具有稳定性
C.三角形的三条中线交于一点
D.三角形的角平分线可能在三角形的内部或外部
3.一个三角形的两边长分别为,,则这个三角形的第三条边的长可能是( )
A. B. C. D.
4.如图图形中,作的边上的高,正确的是( )
A. B.
C. D.
5.把一根长12厘米的铁丝按下面所标长度剪开,剪成的三段首尾顺次相接可以围成三角形的是( )
A. B.
C. D.
6.如图,在△ABC中,D,E分别为BC,AD的中点,且S△ABC=4,则S阴影为( )
A.2 B.1 C. D.
7.如图,已知直线,,,则等于( )
A. B. C. D.
8.如图,AD是△ABC的角平分线,点O在AD上,且OE⊥BC于点E,∠BAC=60°,∠C=80°,则∠EOD的度数为( )
A.20° B.30° C.10° D.15°
9.下列说法正确的是( )
A.一个钝角三角形一定不是等腰三角形,也不是等边三角形
B.一个等腰三角形一定是锐角三角形,或直角三角形
C.一个直角三角形一定不是等腰三角形,也不是等边三角形
D.一个等边三角形一定不是钝角三角形,也不是直角三角形
10.小明把一副直角三角尺按如图所示的方式摆放在一起,则等于( )
A. B. C. D.
二、填空题
11.如下图,的面积为1,分别倍长(延长一倍),,得到,再分别倍长,,得到.…按此规律,倍长2020次后得到的的面积为 .
12.如图,∠A+∠B +∠C +∠D+∠E= 度.
13.为了防止门框变形常常在门框上钉两根斜拉的木条,这样做的数学依据是三角形的 .
14.已知D是△ABC的边BC所在直线上的一点,与B,C不重合,过D分别作DFAC交AB所在直线于F,DEAB交AC所在直线于E.若∠B+∠C=105°,则∠FDE的度数是 .
15.如图,D、E分别是△ABC边AB、BC上的点,AD=2BD,BE=CE,设△ADF的面积为S1,△CEF的面积为S2,若S△ABC=12,则S1﹣S2的值为 .
16.如图,在中,E是的中点,点D在上,且,与交于点F,若,则的面积为 .
三、计算题
17.已知a,b,c是三角形的三边长,化简:.
18.如图,在△ABC中,∠BAC=50°,∠B=60°,AE⊥BC于点E,CD平分∠ACB且分别与AB、AE交于点D、F,求∠AFC的度数.
19.计算题.
(1)已知一个多边形的内角和是1260°,求这个多边形的边数.
(2)用一条长为18cm的细绳围成一个等腰三角形,若有一边长等于4cm,求另外两边长.
四、解答题
20.在中,,,,求的度数.
21.在中,,,求的度数.
22.新定义:在中,若存在最大内角是最小内角度数的n倍(n为大于1的正整数),则称为“n倍角三角形”. 例如,在中,若∠,则,因为最大,最小,且,所以为“3倍角三角形”.
(1)在中,若,则△DEF为“_______倍角三角形”.
(2)如图,在中,的角平分线相交于点D,若为“3倍角三角形”,请求出的度数.
23. 如图,在中.
(1)的角平分线相交于点,求的度数;
(2)的三等分线分别相交于点,求的度数;
(3)的等分线分别相交于点,则 (结果用含的式子表示), (,为整数,结果用含和的式子表示)
答案解析部分
1.【答案】C
【知识点】三角形三边关系
2.【答案】C
【知识点】三角形的角平分线、中线和高;三角形的稳定性
3.【答案】B
【知识点】三角形三边关系
4.【答案】A
【知识点】三角形的角平分线、中线和高
5.【答案】D
【知识点】三角形三边关系
6.【答案】B
【知识点】三角形的角平分线、中线和高
7.【答案】B
【知识点】平行线的性质;三角形的外角性质
8.【答案】A
【知识点】三角形内角和定理;三角形的外角性质
9.【答案】D
【知识点】三角形三边关系
10.【答案】C
【知识点】三角形内角和定理;三角形的外角性质
11.【答案】
【知识点】三角形的角平分线、中线和高
12.【答案】180
【知识点】三角形内角和定理;三角形的外角性质
13.【答案】稳定性
【知识点】三角形的稳定性
14.【答案】75°或105°
【知识点】平行线的性质;三角形内角和定理
15.【答案】2
【知识点】三角形的面积
16.【答案】12
【知识点】三角形的角平分线、中线和高;三角形的面积
17.【答案】
【知识点】整式的加减运算;三角形三边关系;化简含绝对值有理数
18.【答案】解:∵AE⊥BC,∴∠AEB=90°.
∵∠B=60°,
∴∠BAE=90°﹣60°=30°.
∴∠CAE=50°﹣30°=20°
∵∠BAC+∠B+∠ACB=180°,
∴∠ACB=180°﹣∠BAC﹣∠B=70°.
又∵CD平分∠ACB,
∴∠ACD= ∠ACB=35°.
∴∠AFC=180°﹣35°﹣20°=125°.
【知识点】三角形内角和定理;三角形的外角性质;角平分线的概念
19.【答案】(1)9;(2)7 cm ,7 cm.
【知识点】三角形三边关系
20.【答案】
【知识点】三角形的外角性质
21.【答案】
【知识点】三角形内角和定理
22.【答案】(1)2
(2)
【知识点】三角形内角和定理
23.【答案】(1)解:∵ ∠ABC,∠ACB的角平分线相交于点P,
∴ ∠PBC=∠ABC,∠PCB=∠ACB,
∵ ∠A=60°,
∴ ∠BPC=180°-(∠PBC+∠PCB)=180°-(∠ABC+∠ACB)=180°-(180°-∠A)=90°+∠A=120°.
(2)解:∵ ∠ABC,∠ACB的三等分线分别相交于点P1,P2,
∴ ∠P1BC=∠ABC,∠P1CB=∠ACB,
∵ ∠A=60°,
∴ ∠BP1C=180°-(∠P1BC+∠P1CB)=180°-(∠ABC+∠ACB)=180°-(180°-∠A)=120°+∠A=140°,
∵ ∠ABC,∠ACB的三等分线分别相交于点P1,P2,
∴ ∠P2BC=∠ABC,∠P2CB=∠ACB,
∵ ∠A=60°,
∴ ∠BP2C=180°-(∠P2BC+∠P2CB)=180°-(∠ABC+∠ACB)=180°-(180°-∠A)=60°+∠A=100°.
(3);
【知识点】三角形内角和定理;角平分线的概念
21世纪教育网(www.21cnjy.com)
8 / 8
