9.1.4设计轴对称图案(含答案)
文档属性
| 名称 | 9.1.4设计轴对称图案(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 430.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-12 17:32:22 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
9.1.4设计轴对称图案
一、单选题
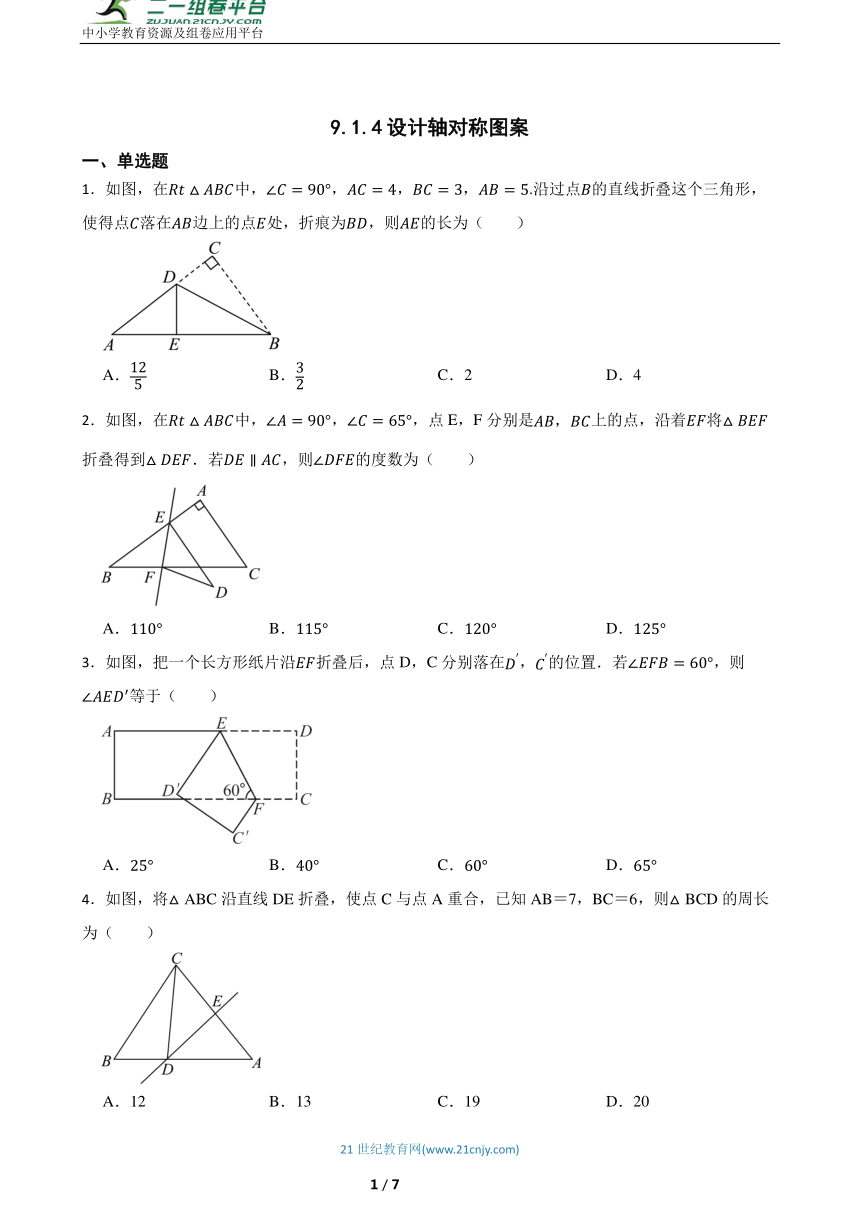
1.如图,在中,,,,.沿过点的直线折叠这个三角形,使得点落在边上的点处,折痕为,则的长为( )
A. B. C.2 D.4
2.如图,在中,,,点E,F分别是上的点,沿着将折叠得到.若,则的度数为( )
A. B. C. D.
3.如图,把一个长方形纸片沿折叠后,点D,C分别落在,的位置.若,则等于( )
A. B. C. D.
4.如图,将△ABC沿直线DE折叠,使点C与点A重合,已知AB=7,BC=6,则△BCD的周长为( )
A.12 B.13 C.19 D.20
5.如图所示,如果将矩形纸沿虚线①对折后,沿虚线②剪开,剪出一个直角三角形,展开后得到一个等腰三角形.则展开后三角形的周长是( )
A.2+ B.2+2 C.12 D.18
二、填空题
6.将一个长方形纸带按如图所示的方式折叠,若,则 .
7.如图,将沿翻折,顶点均落在点处,且与重合于线段,若,则的度数为 .
8.将一条两边互相平行的纸带按如图折叠,设,则 度.
9.将一条两边沿互相平行的纸带按如图折叠,若,则 .
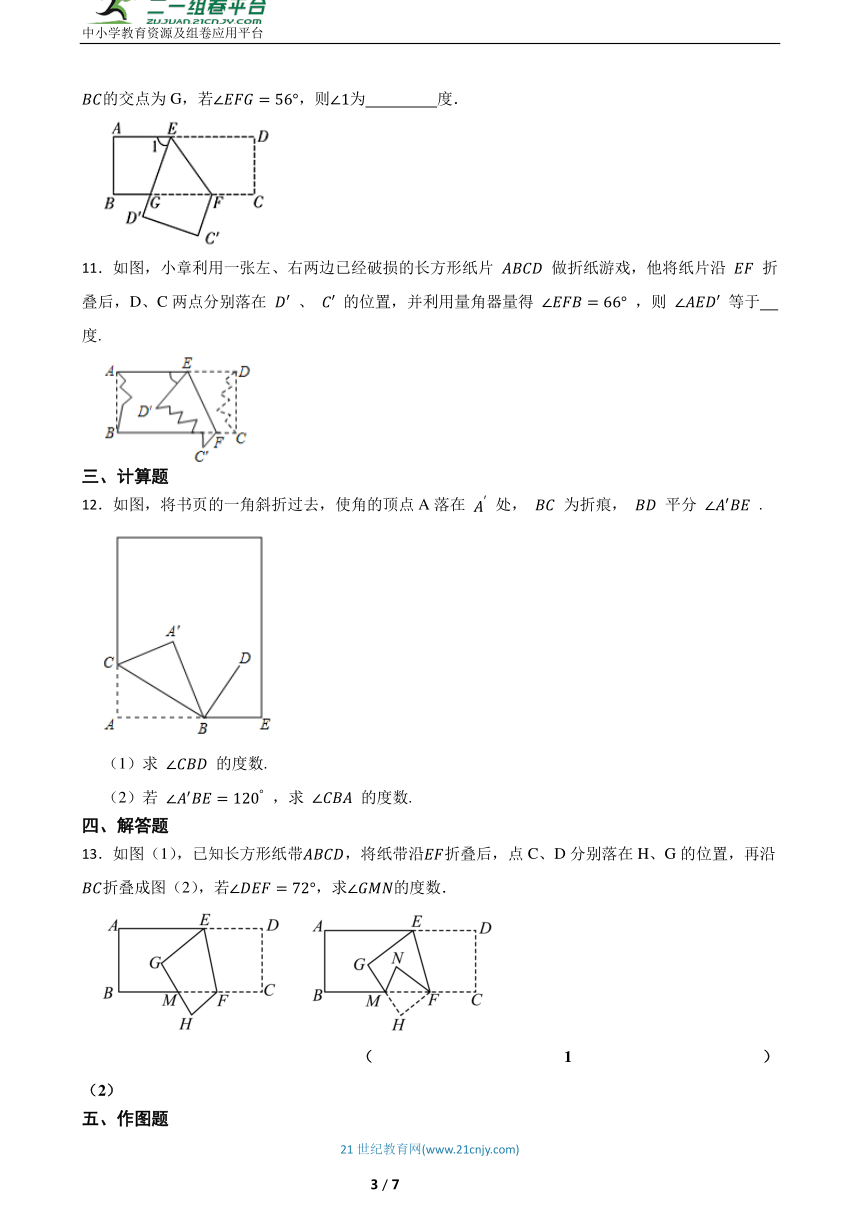
10.如图,把一张长方形纸片沿折叠,点D与点C分别落在点和点的位置上,与的交点为G,若,则为 度.
11.如图,小章利用一张左、右两边已经破损的长方形纸片 做折纸游戏,他将纸片沿 折叠后,D、C两点分别落在 、 的位置,并利用量角器量得 ,则 等于 度.
三、计算题
12.如图,将书页的一角斜折过去,使角的顶点A落在 处, 为折痕, 平分 .
(1)求 的度数.
(2)若 ,求 的度数.
四、解答题
13.如图(1),已知长方形纸带,将纸带沿折叠后,点C、D分别落在H、G的位置,再沿折叠成图(2),若,求的度数.
(1) (2)
五、作图题
14.如图是由5个同样的小正方形所组成的,请再补上一个同样的小正方形,使6个小正方形组成的图形成为一个轴对称图形,请至少画出三种方法.
六、综合题
15.如图,四边形ABCD中,∠BAD=106°,∠BCD=64°,点M,N分别在AB,BC上,得 FMN,若MF∥AD,FN∥DC.
求:
(1)∠F的度数;
(2)∠D的度数.
七、实践探究题
16.综合与实践
折纸是一门古老而有趣的艺术,小明在课余时间进行了关于折纸中角的问题的探索.
初步探索
(1)如图1,四边形纸片中,,点E是线段上一点,将纸片沿折叠,点C的对应点为点,测得,求和的度数;
深入探究
(2)如图2,小明将纸片换成一张长方形纸片(),点E,F分别是线段,上的一点,他先将纸片沿折叠,点A,B的对应点分别为点,与线段交于点G,点H是线段上一点,再将纸片沿折叠,点D的对应点为点,使得点恰好在上,测得,则______
答案解析部分
1.【答案】C
【知识点】翻折变换(折叠问题)
2.【答案】A
【知识点】平行线的性质;三角形内角和定理;翻折变换(折叠问题)
3.【答案】C
【知识点】平行线的性质;翻折变换(折叠问题)
4.【答案】B
【知识点】翻折变换(折叠问题)
5.【答案】B
【知识点】剪纸问题
6.【答案】
【知识点】平行线的性质;翻折变换(折叠问题)
7.【答案】
【知识点】角的运算;三角形内角和定理;翻折变换(折叠问题)
8.【答案】50
【知识点】平行线的性质;翻折变换(折叠问题)
9.【答案】65°
【知识点】翻折变换(折叠问题);内错角的概念;同旁内角的概念
10.【答案】
【知识点】平行线的性质;翻折变换(折叠问题)
11.【答案】48
【知识点】平行线的性质;翻折变换(折叠问题)
12.【答案】(1)解:由折叠的性质可知∠ABC=
∴
又∵BD平分
∴
∵
∴ =
(2)解:∵
∵∠ABC=
∴
【知识点】角的运算;翻折变换(折叠问题);角平分线的概念
13.【答案】
【知识点】平行线的性质;翻折变换(折叠问题)
14.【答案】解:如图所示:
【知识点】利用轴对称设计图案
15.【答案】(1)解:∵MF∥AD,FN∥DC,∠BAD=106°,∠BCD=64°,
∴∠BMF=106°,∠FNB=64°,
∵将△BMN沿MN翻折,得△FMN,
∴∠FMN=∠BMN=53°,∠FNM=∠MNB=32°,
∴∠F=∠B=180°﹣53°﹣32°=95°;
(2)解:∠F=∠B=95°,
∠D=360°﹣106°﹣64°﹣95°=95°.
【知识点】平行线的性质;多边形内角与外角;翻折变换(折叠问题)
16.【答案】(1),;(2)
【知识点】平行线的性质;三角形内角和定理;翻折变换(折叠问题);对顶角及其性质
21世纪教育网(www.21cnjy.com)
2 / 7
9.1.4设计轴对称图案
一、单选题
1.如图,在中,,,,.沿过点的直线折叠这个三角形,使得点落在边上的点处,折痕为,则的长为( )
A. B. C.2 D.4
2.如图,在中,,,点E,F分别是上的点,沿着将折叠得到.若,则的度数为( )
A. B. C. D.
3.如图,把一个长方形纸片沿折叠后,点D,C分别落在,的位置.若,则等于( )
A. B. C. D.
4.如图,将△ABC沿直线DE折叠,使点C与点A重合,已知AB=7,BC=6,则△BCD的周长为( )
A.12 B.13 C.19 D.20
5.如图所示,如果将矩形纸沿虚线①对折后,沿虚线②剪开,剪出一个直角三角形,展开后得到一个等腰三角形.则展开后三角形的周长是( )
A.2+ B.2+2 C.12 D.18
二、填空题
6.将一个长方形纸带按如图所示的方式折叠,若,则 .
7.如图,将沿翻折,顶点均落在点处,且与重合于线段,若,则的度数为 .
8.将一条两边互相平行的纸带按如图折叠,设,则 度.
9.将一条两边沿互相平行的纸带按如图折叠,若,则 .
10.如图,把一张长方形纸片沿折叠,点D与点C分别落在点和点的位置上,与的交点为G,若,则为 度.
11.如图,小章利用一张左、右两边已经破损的长方形纸片 做折纸游戏,他将纸片沿 折叠后,D、C两点分别落在 、 的位置,并利用量角器量得 ,则 等于 度.
三、计算题
12.如图,将书页的一角斜折过去,使角的顶点A落在 处, 为折痕, 平分 .
(1)求 的度数.
(2)若 ,求 的度数.
四、解答题
13.如图(1),已知长方形纸带,将纸带沿折叠后,点C、D分别落在H、G的位置,再沿折叠成图(2),若,求的度数.
(1) (2)
五、作图题
14.如图是由5个同样的小正方形所组成的,请再补上一个同样的小正方形,使6个小正方形组成的图形成为一个轴对称图形,请至少画出三种方法.
六、综合题
15.如图,四边形ABCD中,∠BAD=106°,∠BCD=64°,点M,N分别在AB,BC上,得 FMN,若MF∥AD,FN∥DC.
求:
(1)∠F的度数;
(2)∠D的度数.
七、实践探究题
16.综合与实践
折纸是一门古老而有趣的艺术,小明在课余时间进行了关于折纸中角的问题的探索.
初步探索
(1)如图1,四边形纸片中,,点E是线段上一点,将纸片沿折叠,点C的对应点为点,测得,求和的度数;
深入探究
(2)如图2,小明将纸片换成一张长方形纸片(),点E,F分别是线段,上的一点,他先将纸片沿折叠,点A,B的对应点分别为点,与线段交于点G,点H是线段上一点,再将纸片沿折叠,点D的对应点为点,使得点恰好在上,测得,则______
答案解析部分
1.【答案】C
【知识点】翻折变换(折叠问题)
2.【答案】A
【知识点】平行线的性质;三角形内角和定理;翻折变换(折叠问题)
3.【答案】C
【知识点】平行线的性质;翻折变换(折叠问题)
4.【答案】B
【知识点】翻折变换(折叠问题)
5.【答案】B
【知识点】剪纸问题
6.【答案】
【知识点】平行线的性质;翻折变换(折叠问题)
7.【答案】
【知识点】角的运算;三角形内角和定理;翻折变换(折叠问题)
8.【答案】50
【知识点】平行线的性质;翻折变换(折叠问题)
9.【答案】65°
【知识点】翻折变换(折叠问题);内错角的概念;同旁内角的概念
10.【答案】
【知识点】平行线的性质;翻折变换(折叠问题)
11.【答案】48
【知识点】平行线的性质;翻折变换(折叠问题)
12.【答案】(1)解:由折叠的性质可知∠ABC=
∴
又∵BD平分
∴
∵
∴ =
(2)解:∵
∵∠ABC=
∴
【知识点】角的运算;翻折变换(折叠问题);角平分线的概念
13.【答案】
【知识点】平行线的性质;翻折变换(折叠问题)
14.【答案】解:如图所示:
【知识点】利用轴对称设计图案
15.【答案】(1)解:∵MF∥AD,FN∥DC,∠BAD=106°,∠BCD=64°,
∴∠BMF=106°,∠FNB=64°,
∵将△BMN沿MN翻折,得△FMN,
∴∠FMN=∠BMN=53°,∠FNM=∠MNB=32°,
∴∠F=∠B=180°﹣53°﹣32°=95°;
(2)解:∠F=∠B=95°,
∠D=360°﹣106°﹣64°﹣95°=95°.
【知识点】平行线的性质;多边形内角与外角;翻折变换(折叠问题)
16.【答案】(1),;(2)
【知识点】平行线的性质;三角形内角和定理;翻折变换(折叠问题);对顶角及其性质
21世纪教育网(www.21cnjy.com)
2 / 7
