9.1轴对称综合题(含答案)
图片预览



文档简介
中小学教育资源及组卷应用平台
9.1轴对称综合题
一、单选题
1.剪纸是中国古老的汉族传统民间艺术之一.下面
是制作剪纸的简单流程,展开后的剪纸图案从对称性来判断( )
A.是轴对称图形但不是中心对称图形
B.是中心对称图形但不是轴对称图形
C.既是轴对称图形也是中心对称图形
D.既不是轴对称图形也不是中心对称图形
2.在一些美术字中,有的汉字是轴对称图形.下面几个汉字中,可看作是轴对称图形的是( )
A.中 B.考 C.加 D.油
3.在平面直角坐标系中,△OAB各顶点的坐标分别为:O(0,0),A(1,2),B(0,3),以O为位似中心,△OA′B′与△OAB位似,若B点的对应点B′的坐标为(0,-6),则A点的对应点A′坐标为( )
A.(-2,-4) B.(-4,-2)
C.(-1,-4) D.(1,-4)
4.下列美术字中可以看作是轴对称图形的是( )
A. B.
C. D.
5.下列防控“新冠肺炎”的图片中,是轴对称图形的是( )
A. B. C. D.
6.在平面直角坐标系中,点A(2,3)与点B关于x轴对称,则点B的坐标为( )
A.(3,2) B.(-2,-3) C.(-2,3) D.(2,-3)
7.下列图形中,是轴对称图形的是( )
A. B. C. D.
8.2016年是中国农历丙申猴年,下列四个猴子头像中,是轴对称图形的是( )
A. B. C. D.
9.如图,在下列四个图形中,是轴对称图形的是( )
A. B.
C. D.
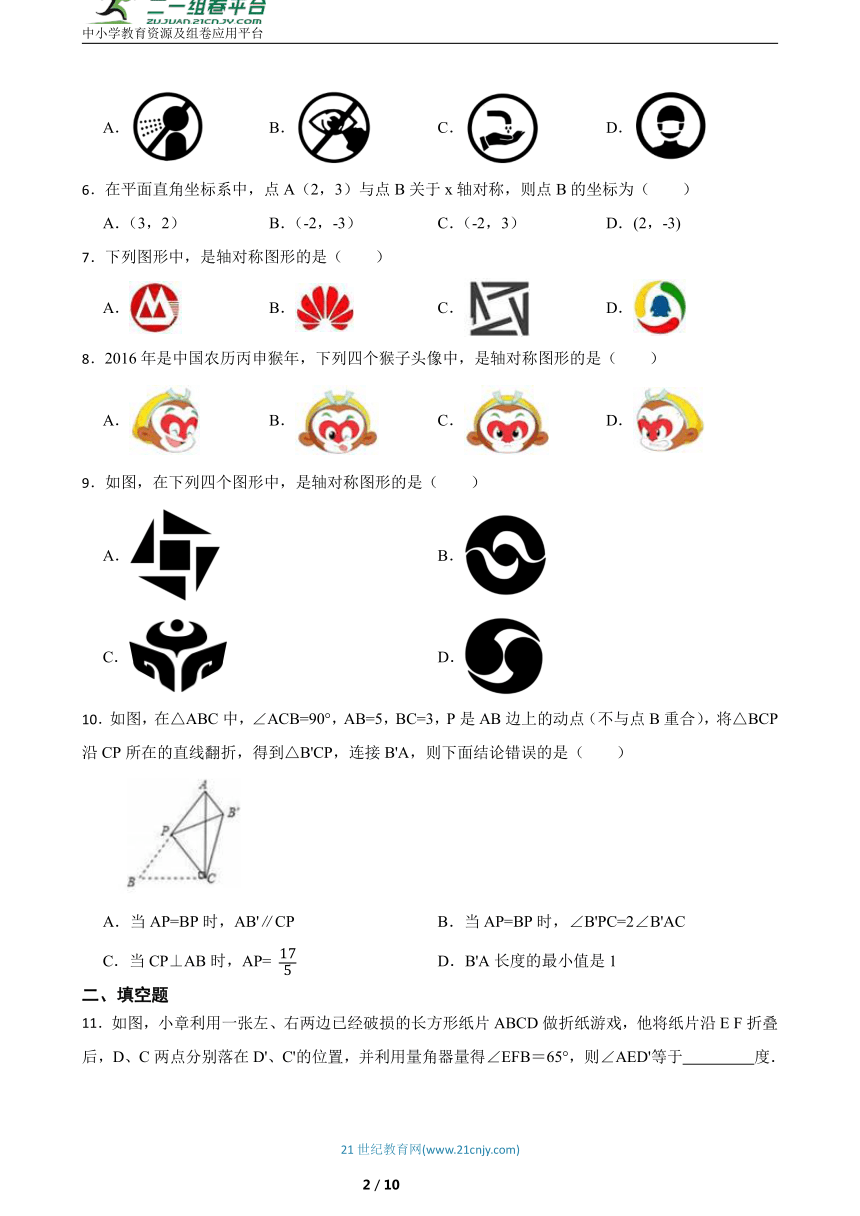
10.如图,在△ABC中,∠ACB=90°,AB=5,BC=3,P是AB边上的动点(不与点B重合),将△BCP沿CP所在的直线翻折,得到△B'CP,连接B'A,则下面结论错误的是( )
A.当AP=BP时,AB'∥CP B.当AP=BP时,∠B'PC=2∠B'AC
C.当CP⊥AB时,AP= D.B'A长度的最小值是1
二、填空题
11.如图,小章利用一张左、右两边已经破损的长方形纸片ABCD做折纸游戏,他将纸片沿E F折叠后,D、C两点分别落在D'、C'的位置,并利用量角器量得∠EFB=65°,则∠AED'等于 度.
12.如图,已知,为内任一点,且,请在图中分别画出点关于,的对称点,,连,,,则的面积为 .
13.任何一条线段都是轴对称图形.
14. 如图,把一张长方形纸片沿折叠后,分别落在的位置上,与交于点,若,则 .
15.如图,在中,,将其折叠,使点A落在边BC上的点E处,CA与CE重合,折痕为CD,则的度数是 .
16.如图,在中,平分交于点,点,分别是线段、上一动点,且,,则的最小值为 .
三、计算题
17.如图,△ABC三个顶点的坐标分别为、、.
(1)若与△ABC关于y轴成轴对称,则三个顶点坐标分别为: , ;
(2)若P为y轴上一点,则的最小值为 ;
(3)计算的面积.
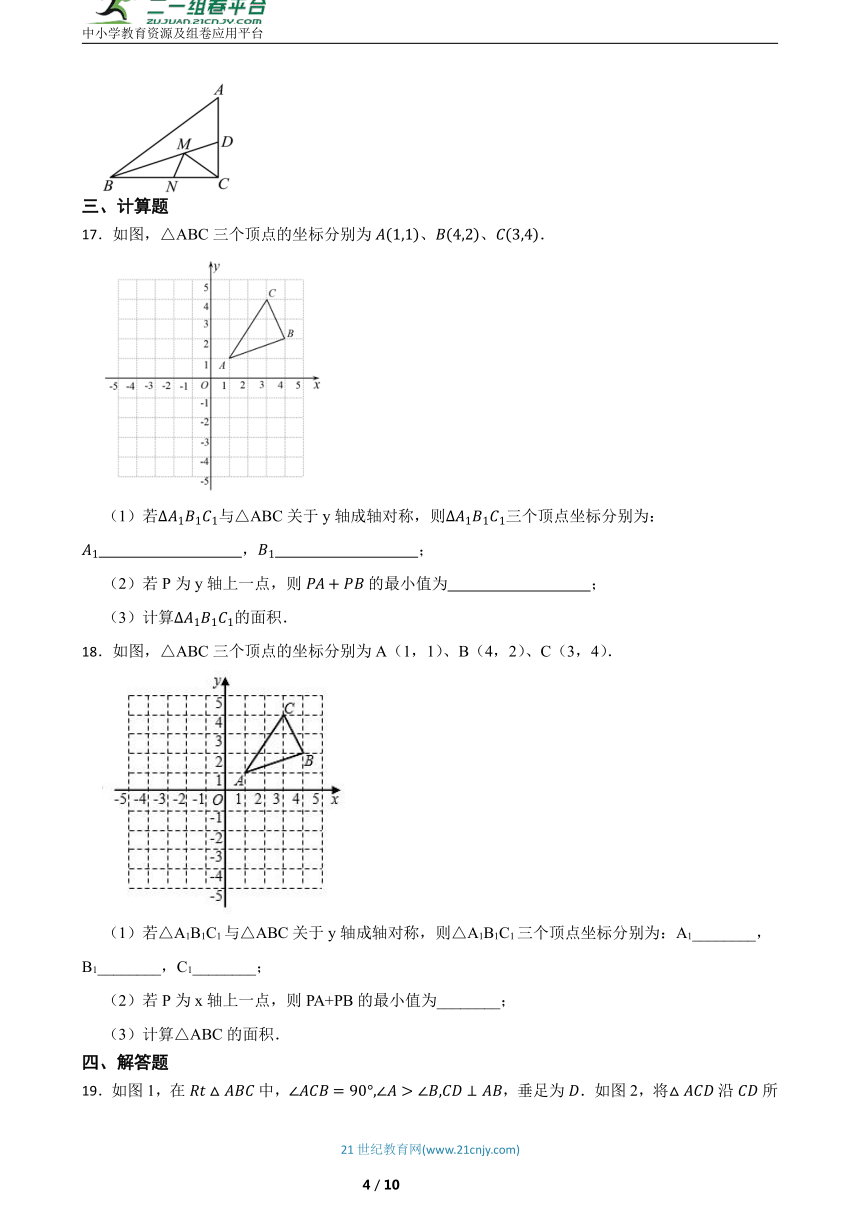
18.如图,△ABC三个顶点的坐标分别为A(1,1)、B(4,2)、C(3,4).
(1)若△A1B1C1与△ABC关于y轴成轴对称,则△A1B1C1三个顶点坐标分别为:A1________,B1________,C1________;
(2)若P为x轴上一点,则PA+PB的最小值为________;
(3)计算△ABC的面积.
四、解答题
19.如图1,在中,,垂足为.如图2,将沿所在直线翻折,使点落在边上,记为.
(1)若,求的度数.
(2)若,则的度数为______(用含的代数式表示).
20.如图,长方形纸片,点分别在边上,连接,将对折,点落在直线上的点处,得到折痕;将对折,点落在直线的处,得到折痕.
(1)若 ,的余角有 ;
(2)若 ,说明理由.
21.如图,在数轴上点A表示数a,点B表示数b,点C表示数c,点A到点B的距离记为,我们规定:的大小可以用位于右边的点表示的数减去左边的点表示的数表示,即.其中b是最大的负整数,a,c满足与互为相反数.
(1) , , ;
(2)以某点D为折点,将此数轴向右对折,若点A在点C的右边,且,则D表示的数是 ;
(3)若点A以每秒2个单位长度的速度向右运动t秒时,.求出t的值.
22.长方形纸片OABC中,AB=10cm,BC=6cm,把这张长方形纸片OABC如图放置在平面直角坐标系中,在边OA上取一点E,将△ABE沿BE折叠,使点A恰好落在OC边上的点F处.
(1)求点E、F的坐标;
(2)在AB上找一点P,使PE+PF最小,求点P坐标;
(3)在(2)的条件下,点Q(x,y)是直线PF上一个动点,设△OCQ的面积为S,求S与x的函数关系式.
答案解析部分
1.【答案】C
【知识点】轴对称图形
2.【答案】A
【知识点】轴对称图形
3.【答案】A
【知识点】坐标与图形变化﹣对称
4.【答案】A
【知识点】轴对称图形
5.【答案】D
【知识点】轴对称图形
6.【答案】D
【知识点】坐标与图形变化﹣对称
7.【答案】B
【知识点】轴对称的性质;轴对称图形
8.【答案】C
【知识点】轴对称图形
9.【答案】C
【知识点】轴对称图形
10.【答案】C
【知识点】翻折变换(折叠问题)
11.【答案】50
【知识点】翻折变换(折叠问题)
12.【答案】
【知识点】轴对称的性质
13.【答案】正确
【知识点】直线、射线、线段;轴对称图形
14.【答案】68°
【知识点】平行线的性质;翻折变换(折叠问题)
15.【答案】14°
【知识点】三角形内角和定理;三角形的外角性质;翻折变换(折叠问题)
16.【答案】4
【知识点】垂线段最短及其应用;轴对称的性质
17.【答案】(1),
(2)
(3)
【知识点】两点之间线段最短;坐标与图形变化﹣对称;作图﹣轴对称
18.【答案】(1)(-1,1),(-4,2),(-3,4);(2);(3).
【知识点】两点之间线段最短;坐标与图形变化﹣对称
19.【答案】(1)
(2)
【知识点】三角形内角和定理;三角形的外角性质;翻折变换(折叠问题)
20.【答案】(1);和;
(2)
【知识点】角的运算;翻折变换(折叠问题)
21.【答案】(1),,
(2)2
(3)秒或秒
【知识点】一元一次方程的其他应用;翻折变换(折叠问题);绝对值的非负性
22.【答案】(1)解:设OE=x,则AE=6-x,
由折叠知BA=BF=10,EF=AE=6-x,
∵四边形OABC是长方形,
∴∠BCO=90°,
∴CF= =8,
∴OF=OC-CF=10-8=2,
∴点F的坐标为(-2,0),
在Rt△EOF中,EF2=OF2+OE2,即(6-x)2=22+x2,
解得,x= ,
∴点E的坐标为(0, ),
∴点E的坐标为(0, ),点F的坐标为(-2,0)
(2)解:作E关于AB的对称点E′,连结FE′,交AB于P,
则PE+PF最小最小,
∵点E的坐标为(0, ),
∴AE=6- = ,
∵点E与点E′关于AB对称,
∴AE′=AE= ,
∴OE′= +6= ,
∴点E′的坐标为(0, ),
设直线FE′的解析式为y=kx+b,
则 ,
解得,k= ,b= ,
则直线FE′的解析式为y= x+ ,
当y=6时, x+ =6,
解得,x=- ,
∴点P的坐标为(- ,6)
(3)解:设点Q的坐标为(x, x+ ),
当Q在x轴上方时,即x>-2时,S= ×10×( x+ )= x+ ,
当Q在x轴下方时,即x<-2时,S= ×10×(- x- )=- x- ,
综上所述,S= .
【知识点】翻折变换(折叠问题)
21世纪教育网(www.21cnjy.com)
1 / 10
9.1轴对称综合题
一、单选题
1.剪纸是中国古老的汉族传统民间艺术之一.下面
是制作剪纸的简单流程,展开后的剪纸图案从对称性来判断( )
A.是轴对称图形但不是中心对称图形
B.是中心对称图形但不是轴对称图形
C.既是轴对称图形也是中心对称图形
D.既不是轴对称图形也不是中心对称图形
2.在一些美术字中,有的汉字是轴对称图形.下面几个汉字中,可看作是轴对称图形的是( )
A.中 B.考 C.加 D.油
3.在平面直角坐标系中,△OAB各顶点的坐标分别为:O(0,0),A(1,2),B(0,3),以O为位似中心,△OA′B′与△OAB位似,若B点的对应点B′的坐标为(0,-6),则A点的对应点A′坐标为( )
A.(-2,-4) B.(-4,-2)
C.(-1,-4) D.(1,-4)
4.下列美术字中可以看作是轴对称图形的是( )
A. B.
C. D.
5.下列防控“新冠肺炎”的图片中,是轴对称图形的是( )
A. B. C. D.
6.在平面直角坐标系中,点A(2,3)与点B关于x轴对称,则点B的坐标为( )
A.(3,2) B.(-2,-3) C.(-2,3) D.(2,-3)
7.下列图形中,是轴对称图形的是( )
A. B. C. D.
8.2016年是中国农历丙申猴年,下列四个猴子头像中,是轴对称图形的是( )
A. B. C. D.
9.如图,在下列四个图形中,是轴对称图形的是( )
A. B.
C. D.
10.如图,在△ABC中,∠ACB=90°,AB=5,BC=3,P是AB边上的动点(不与点B重合),将△BCP沿CP所在的直线翻折,得到△B'CP,连接B'A,则下面结论错误的是( )
A.当AP=BP时,AB'∥CP B.当AP=BP时,∠B'PC=2∠B'AC
C.当CP⊥AB时,AP= D.B'A长度的最小值是1
二、填空题
11.如图,小章利用一张左、右两边已经破损的长方形纸片ABCD做折纸游戏,他将纸片沿E F折叠后,D、C两点分别落在D'、C'的位置,并利用量角器量得∠EFB=65°,则∠AED'等于 度.
12.如图,已知,为内任一点,且,请在图中分别画出点关于,的对称点,,连,,,则的面积为 .
13.任何一条线段都是轴对称图形.
14. 如图,把一张长方形纸片沿折叠后,分别落在的位置上,与交于点,若,则 .
15.如图,在中,,将其折叠,使点A落在边BC上的点E处,CA与CE重合,折痕为CD,则的度数是 .
16.如图,在中,平分交于点,点,分别是线段、上一动点,且,,则的最小值为 .
三、计算题
17.如图,△ABC三个顶点的坐标分别为、、.
(1)若与△ABC关于y轴成轴对称,则三个顶点坐标分别为: , ;
(2)若P为y轴上一点,则的最小值为 ;
(3)计算的面积.
18.如图,△ABC三个顶点的坐标分别为A(1,1)、B(4,2)、C(3,4).
(1)若△A1B1C1与△ABC关于y轴成轴对称,则△A1B1C1三个顶点坐标分别为:A1________,B1________,C1________;
(2)若P为x轴上一点,则PA+PB的最小值为________;
(3)计算△ABC的面积.
四、解答题
19.如图1,在中,,垂足为.如图2,将沿所在直线翻折,使点落在边上,记为.
(1)若,求的度数.
(2)若,则的度数为______(用含的代数式表示).
20.如图,长方形纸片,点分别在边上,连接,将对折,点落在直线上的点处,得到折痕;将对折,点落在直线的处,得到折痕.
(1)若 ,的余角有 ;
(2)若 ,说明理由.
21.如图,在数轴上点A表示数a,点B表示数b,点C表示数c,点A到点B的距离记为,我们规定:的大小可以用位于右边的点表示的数减去左边的点表示的数表示,即.其中b是最大的负整数,a,c满足与互为相反数.
(1) , , ;
(2)以某点D为折点,将此数轴向右对折,若点A在点C的右边,且,则D表示的数是 ;
(3)若点A以每秒2个单位长度的速度向右运动t秒时,.求出t的值.
22.长方形纸片OABC中,AB=10cm,BC=6cm,把这张长方形纸片OABC如图放置在平面直角坐标系中,在边OA上取一点E,将△ABE沿BE折叠,使点A恰好落在OC边上的点F处.
(1)求点E、F的坐标;
(2)在AB上找一点P,使PE+PF最小,求点P坐标;
(3)在(2)的条件下,点Q(x,y)是直线PF上一个动点,设△OCQ的面积为S,求S与x的函数关系式.
答案解析部分
1.【答案】C
【知识点】轴对称图形
2.【答案】A
【知识点】轴对称图形
3.【答案】A
【知识点】坐标与图形变化﹣对称
4.【答案】A
【知识点】轴对称图形
5.【答案】D
【知识点】轴对称图形
6.【答案】D
【知识点】坐标与图形变化﹣对称
7.【答案】B
【知识点】轴对称的性质;轴对称图形
8.【答案】C
【知识点】轴对称图形
9.【答案】C
【知识点】轴对称图形
10.【答案】C
【知识点】翻折变换(折叠问题)
11.【答案】50
【知识点】翻折变换(折叠问题)
12.【答案】
【知识点】轴对称的性质
13.【答案】正确
【知识点】直线、射线、线段;轴对称图形
14.【答案】68°
【知识点】平行线的性质;翻折变换(折叠问题)
15.【答案】14°
【知识点】三角形内角和定理;三角形的外角性质;翻折变换(折叠问题)
16.【答案】4
【知识点】垂线段最短及其应用;轴对称的性质
17.【答案】(1),
(2)
(3)
【知识点】两点之间线段最短;坐标与图形变化﹣对称;作图﹣轴对称
18.【答案】(1)(-1,1),(-4,2),(-3,4);(2);(3).
【知识点】两点之间线段最短;坐标与图形变化﹣对称
19.【答案】(1)
(2)
【知识点】三角形内角和定理;三角形的外角性质;翻折变换(折叠问题)
20.【答案】(1);和;
(2)
【知识点】角的运算;翻折变换(折叠问题)
21.【答案】(1),,
(2)2
(3)秒或秒
【知识点】一元一次方程的其他应用;翻折变换(折叠问题);绝对值的非负性
22.【答案】(1)解:设OE=x,则AE=6-x,
由折叠知BA=BF=10,EF=AE=6-x,
∵四边形OABC是长方形,
∴∠BCO=90°,
∴CF= =8,
∴OF=OC-CF=10-8=2,
∴点F的坐标为(-2,0),
在Rt△EOF中,EF2=OF2+OE2,即(6-x)2=22+x2,
解得,x= ,
∴点E的坐标为(0, ),
∴点E的坐标为(0, ),点F的坐标为(-2,0)
(2)解:作E关于AB的对称点E′,连结FE′,交AB于P,
则PE+PF最小最小,
∵点E的坐标为(0, ),
∴AE=6- = ,
∵点E与点E′关于AB对称,
∴AE′=AE= ,
∴OE′= +6= ,
∴点E′的坐标为(0, ),
设直线FE′的解析式为y=kx+b,
则 ,
解得,k= ,b= ,
则直线FE′的解析式为y= x+ ,
当y=6时, x+ =6,
解得,x=- ,
∴点P的坐标为(- ,6)
(3)解:设点Q的坐标为(x, x+ ),
当Q在x轴上方时,即x>-2时,S= ×10×( x+ )= x+ ,
当Q在x轴下方时,即x<-2时,S= ×10×(- x- )=- x- ,
综上所述,S= .
【知识点】翻折变换(折叠问题)
21世纪教育网(www.21cnjy.com)
1 / 10
