9.3.2旋转的特征(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
9.3.2旋转的特征
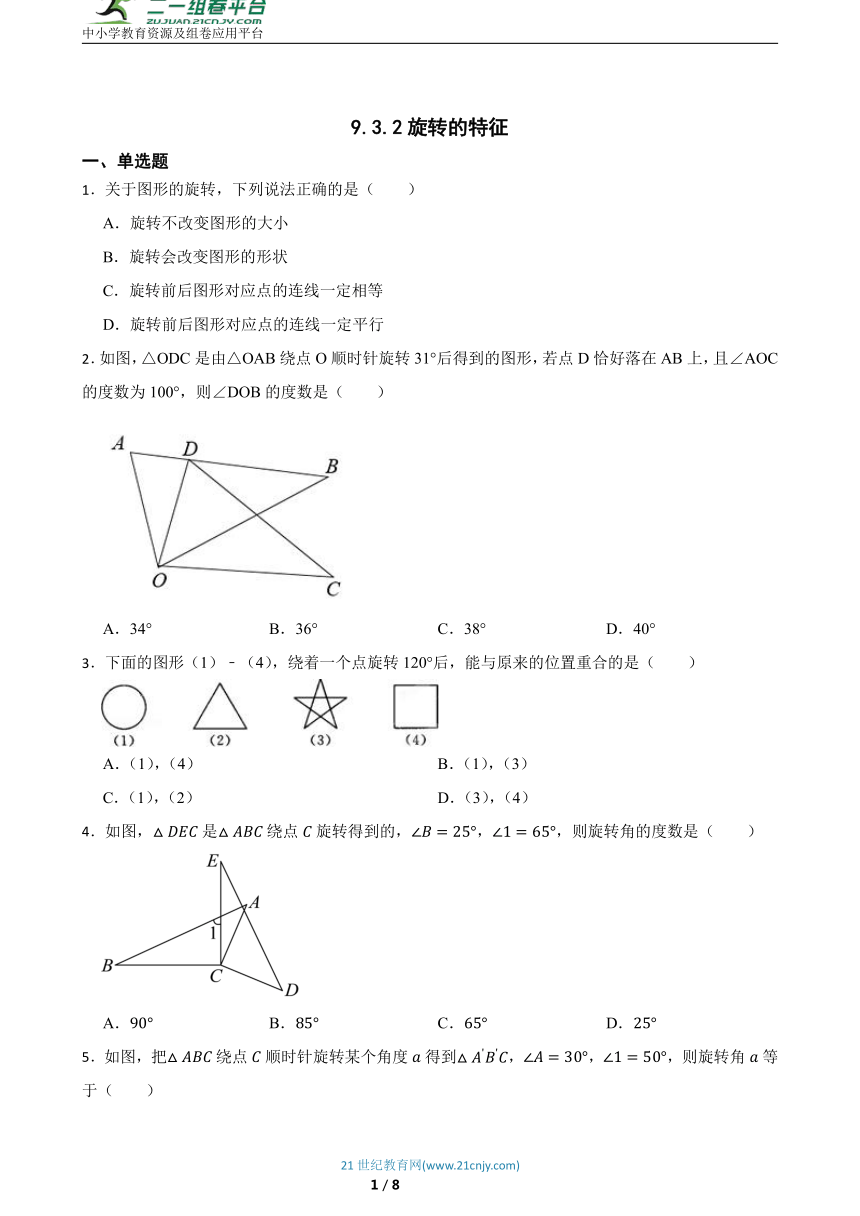
一、单选题
1.关于图形的旋转,下列说法正确的是( )
A.旋转不改变图形的大小
B.旋转会改变图形的形状
C.旋转前后图形对应点的连线一定相等
D.旋转前后图形对应点的连线一定平行
2.如图,△ODC是由△OAB绕点O顺时针旋转31°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为100°,则∠DOB的度数是( )
A.34° B.36° C.38° D.40°
3.下面的图形(1)﹣(4),绕着一个点旋转120°后,能与原来的位置重合的是( )
A.(1),(4) B.(1),(3)
C.(1),(2) D.(3),(4)
4.如图,是绕点旋转得到的,,,则旋转角的度数是( )
A. B. C. D.
5.如图,把绕点顺时针旋转某个角度得到,,,则旋转角等于( )
A. B. C. D.
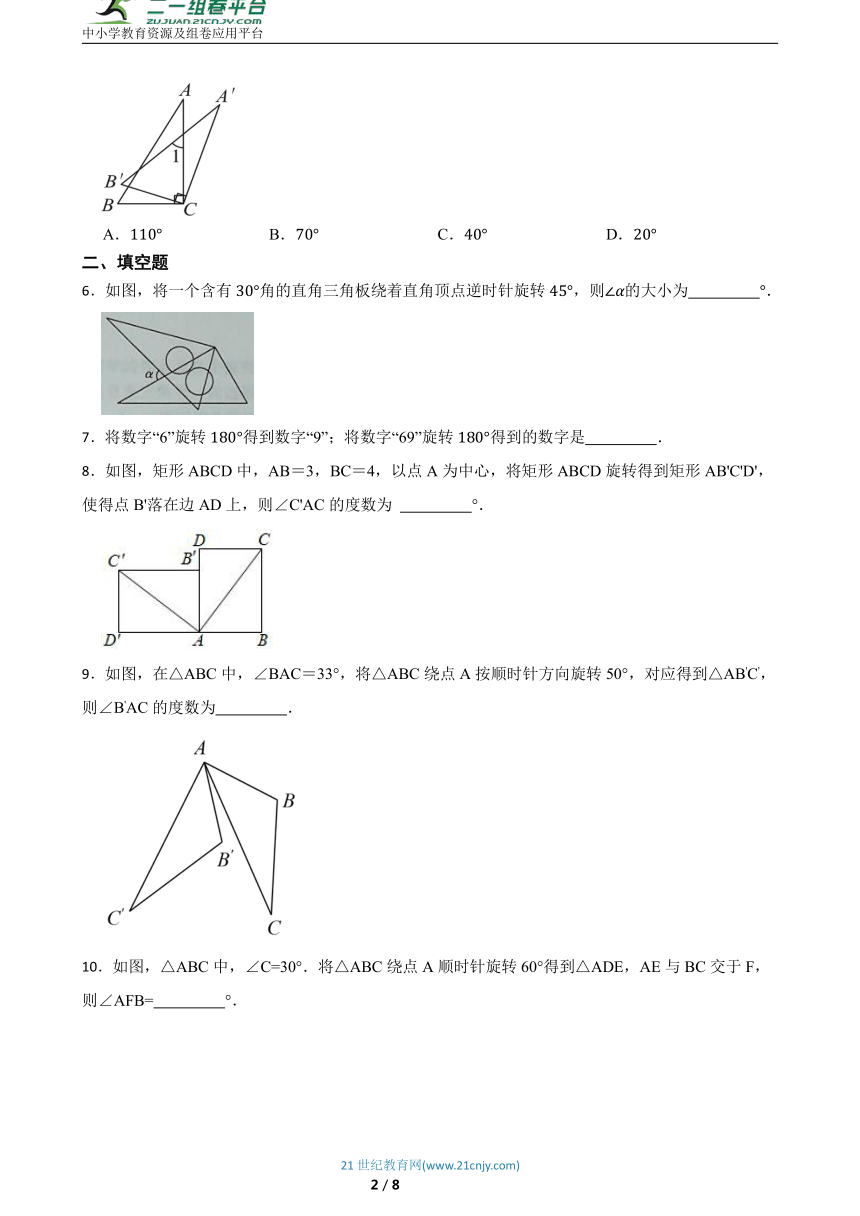
二、填空题
6.如图,将一个含有角的直角三角板绕着直角顶点逆时针旋转,则的大小为 .
7.将数字“6”旋转得到数字“9”;将数字“69”旋转得到的数字是 .
8.如图,矩形ABCD中,AB=3,BC=4,以点A为中心,将矩形ABCD旋转得到矩形AB'C'D',使得点B'落在边AD上,则∠C'AC的度数为 °.
9.如图,在△ABC中,∠BAC=33°,将△ABC绕点A按顺时针方向旋转50°,对应得到△AB'C',则∠B'AC的度数为 .
10.如图,△ABC中,∠C=30°.将△ABC绕点A顺时针旋转60°得到△ADE,AE与BC交于F,则∠AFB= °.
11.如图,以点O为旋转中心,将按顺时针方向旋转得到,若,则 度.
三、计算题
12.如图,将△ABC绕点C顺时针旋转90°后得△DEC,若BC∥DE,求∠B的度数.
四、解答题
13.如图,△ABC的顶点坐标分别为A(4,6)、B(5,2)、C(2,1),如果将△ABC绕点C按逆时针方向旋转90゜,得到△A′B′C′,画图,并写出点A的对应点A′的坐标及B点的对应点B′的坐标.
五、作图题
14.如图,在以边长为1的小正方形组成的网格中,的三个顶点均在格点上.以点A为旋转中心,将按顺时针方向旋转,画出旋转后的,点B,C的对应点分别为,.
六、综合题
15.在边长为1的正方形网格中,△AOB的位置如图所示.
(1)将△OAB绕着点O逆时针旋转90°,画出旋转后得到的△OCD;
(2)直接写出旋转过程中,点A所经过路径的长为 .
16.如图,△ABC中,∠B=10°,∠ACB=20°,AB=4cm,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD的中点.
(1)指出旋转中心,并求出旋转的度数;
(2)求出∠BAE的度数和AE的长.
17.已知:方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).
(1)请以原点O为对称点,画出与△ABC对称的△A1B1C1,并直接写出点A1、B1、C1的坐标;
(2)△ABC的面积是 .
七、实践探究题
18.数学综合实践课上,小明用一块直角三角板进行探究:将三角板的直角顶点O放在直线上,将边落在射线上,边位于直线上方,三角板 绕点O顺时针旋转,旋转角为a,作直线平分交所在直线于点E.
(1)提出问题:如图1,若旋转角,求的度数;
(2)探索发现:如图2,若旋转角时,求的值;
(3)拓展探究:继续旋转三角板,若旋转角时,此时与还存在(2)中的结论吗?若存在,说明理由;如不存在,直接写出与之间的关系.
答案解析部分
1.【答案】A
【知识点】旋转的性质
2.【答案】C
【知识点】旋转的性质
3.【答案】C
【知识点】旋转的性质
4.【答案】A
【知识点】三角形内角和定理;旋转的性质
5.【答案】D
【知识点】三角形的外角性质;旋转的性质
6.【答案】75
【知识点】三角形的外角性质;旋转的性质
7.【答案】69
【知识点】旋转的性质
8.【答案】90
【知识点】角的运算;旋转的性质
9.【答案】17°
【知识点】旋转的性质
10.【答案】90
【知识点】三角形的外角性质;旋转的性质
11.【答案】
【知识点】旋转的性质
12.【答案】解:∵将△ABC绕点C顺时针旋转90°后得△DEC,
∴∠BCE=90°,∠E=∠B,
∵BC∥DE,
∴∠E=180°﹣∠BCE=90°,
∴∠B=90°.
【知识点】平行线的性质;旋转的性质
13.【答案】解:如图所示:△A′B′C′即为所求,A′的坐标为:(﹣3,3),B′的坐标为:(1,4).
【知识点】作图﹣旋转
14.【答案】解:如图,即为所求.
【知识点】作图﹣旋转
15.【答案】(1)解:如图
(2)
【知识点】作图﹣旋转
16.【答案】(1)解:∵△ABC逆时针旋转一定角度后与△ADE重合,A为顶点, ∴旋转中心是点A; 根据旋转的性质可知:∠CAE=∠BAD=180°-∠B-∠ACB=150°, ∴旋转角度是150°
(2)解:由(1)可知:∠BAE=360°-150°×2=60°, 由旋转可知:△ABC≌△ADE, ∴AB=AD,AC=AE,又C为AD中点, ∴AC=AE= AB= ×4=2cm.
【知识点】旋转的性质
17.【答案】(1)解:如图所示,点A1(﹣1,4)点B1(﹣5,4),点C1(﹣4,1).
(2)6
【知识点】旋转的性质;作图﹣旋转
18.【答案】(1)
(2)
(3)不存在,
【知识点】角的运算;余角、补角及其性质;旋转的性质
21世纪教育网(www.21cnjy.com)
8 / 8
9.3.2旋转的特征
一、单选题
1.关于图形的旋转,下列说法正确的是( )
A.旋转不改变图形的大小
B.旋转会改变图形的形状
C.旋转前后图形对应点的连线一定相等
D.旋转前后图形对应点的连线一定平行
2.如图,△ODC是由△OAB绕点O顺时针旋转31°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为100°,则∠DOB的度数是( )
A.34° B.36° C.38° D.40°
3.下面的图形(1)﹣(4),绕着一个点旋转120°后,能与原来的位置重合的是( )
A.(1),(4) B.(1),(3)
C.(1),(2) D.(3),(4)
4.如图,是绕点旋转得到的,,,则旋转角的度数是( )
A. B. C. D.
5.如图,把绕点顺时针旋转某个角度得到,,,则旋转角等于( )
A. B. C. D.
二、填空题
6.如图,将一个含有角的直角三角板绕着直角顶点逆时针旋转,则的大小为 .
7.将数字“6”旋转得到数字“9”;将数字“69”旋转得到的数字是 .
8.如图,矩形ABCD中,AB=3,BC=4,以点A为中心,将矩形ABCD旋转得到矩形AB'C'D',使得点B'落在边AD上,则∠C'AC的度数为 °.
9.如图,在△ABC中,∠BAC=33°,将△ABC绕点A按顺时针方向旋转50°,对应得到△AB'C',则∠B'AC的度数为 .
10.如图,△ABC中,∠C=30°.将△ABC绕点A顺时针旋转60°得到△ADE,AE与BC交于F,则∠AFB= °.
11.如图,以点O为旋转中心,将按顺时针方向旋转得到,若,则 度.
三、计算题
12.如图,将△ABC绕点C顺时针旋转90°后得△DEC,若BC∥DE,求∠B的度数.
四、解答题
13.如图,△ABC的顶点坐标分别为A(4,6)、B(5,2)、C(2,1),如果将△ABC绕点C按逆时针方向旋转90゜,得到△A′B′C′,画图,并写出点A的对应点A′的坐标及B点的对应点B′的坐标.
五、作图题
14.如图,在以边长为1的小正方形组成的网格中,的三个顶点均在格点上.以点A为旋转中心,将按顺时针方向旋转,画出旋转后的,点B,C的对应点分别为,.
六、综合题
15.在边长为1的正方形网格中,△AOB的位置如图所示.
(1)将△OAB绕着点O逆时针旋转90°,画出旋转后得到的△OCD;
(2)直接写出旋转过程中,点A所经过路径的长为 .
16.如图,△ABC中,∠B=10°,∠ACB=20°,AB=4cm,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD的中点.
(1)指出旋转中心,并求出旋转的度数;
(2)求出∠BAE的度数和AE的长.
17.已知:方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).
(1)请以原点O为对称点,画出与△ABC对称的△A1B1C1,并直接写出点A1、B1、C1的坐标;
(2)△ABC的面积是 .
七、实践探究题
18.数学综合实践课上,小明用一块直角三角板进行探究:将三角板的直角顶点O放在直线上,将边落在射线上,边位于直线上方,三角板 绕点O顺时针旋转,旋转角为a,作直线平分交所在直线于点E.
(1)提出问题:如图1,若旋转角,求的度数;
(2)探索发现:如图2,若旋转角时,求的值;
(3)拓展探究:继续旋转三角板,若旋转角时,此时与还存在(2)中的结论吗?若存在,说明理由;如不存在,直接写出与之间的关系.
答案解析部分
1.【答案】A
【知识点】旋转的性质
2.【答案】C
【知识点】旋转的性质
3.【答案】C
【知识点】旋转的性质
4.【答案】A
【知识点】三角形内角和定理;旋转的性质
5.【答案】D
【知识点】三角形的外角性质;旋转的性质
6.【答案】75
【知识点】三角形的外角性质;旋转的性质
7.【答案】69
【知识点】旋转的性质
8.【答案】90
【知识点】角的运算;旋转的性质
9.【答案】17°
【知识点】旋转的性质
10.【答案】90
【知识点】三角形的外角性质;旋转的性质
11.【答案】
【知识点】旋转的性质
12.【答案】解:∵将△ABC绕点C顺时针旋转90°后得△DEC,
∴∠BCE=90°,∠E=∠B,
∵BC∥DE,
∴∠E=180°﹣∠BCE=90°,
∴∠B=90°.
【知识点】平行线的性质;旋转的性质
13.【答案】解:如图所示:△A′B′C′即为所求,A′的坐标为:(﹣3,3),B′的坐标为:(1,4).
【知识点】作图﹣旋转
14.【答案】解:如图,即为所求.
【知识点】作图﹣旋转
15.【答案】(1)解:如图
(2)
【知识点】作图﹣旋转
16.【答案】(1)解:∵△ABC逆时针旋转一定角度后与△ADE重合,A为顶点, ∴旋转中心是点A; 根据旋转的性质可知:∠CAE=∠BAD=180°-∠B-∠ACB=150°, ∴旋转角度是150°
(2)解:由(1)可知:∠BAE=360°-150°×2=60°, 由旋转可知:△ABC≌△ADE, ∴AB=AD,AC=AE,又C为AD中点, ∴AC=AE= AB= ×4=2cm.
【知识点】旋转的性质
17.【答案】(1)解:如图所示,点A1(﹣1,4)点B1(﹣5,4),点C1(﹣4,1).
(2)6
【知识点】旋转的性质;作图﹣旋转
18.【答案】(1)
(2)
(3)不存在,
【知识点】角的运算;余角、补角及其性质;旋转的性质
21世纪教育网(www.21cnjy.com)
8 / 8
