2024—2025学年人教版七年级数学上册7.1.1 两条直线相交 课件 (共42张PPT)
文档属性
| 名称 | 2024—2025学年人教版七年级数学上册7.1.1 两条直线相交 课件 (共42张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-13 00:00:00 | ||
图片预览








文档简介
(共42张PPT)
第七章 相交线与平行线
7.1 相交线
7.1.1 两条直线相交
目
录
1. 学习目标
4. 知识点1 邻补角与对顶角的概念
6. 课堂小结
7. 当堂小练
CONTENTS
3. 新课导入
5. 知识点2 邻补角与对顶角的性质
9. 拓展与延伸
2. 知识回顾
8. 对接中考
1. 理解两条直线相交的特征及邻补角与对顶角的概念.
2. 掌握对顶角相等的性质.
3. 运用对顶角与邻补角的性质进行有关的推理或计算.
学习目标
知识回顾
如果两个角的和等于90°(直角),就说这两个角互为余角
余角和补角
定义
性质
同角(等角)的余角相等
补角
如果两个角的和等于180°(平角),就说这两个角互为补角
定义
性质
同角(等角)的补角相等
余角
新课导入
【复习】用适当的语句表述图中点与直线的关系.
解:如图 ,直线a,b,c两两相交,
直线b与直线c相交于点A,
直线a与直线c相交于点B,
直线a与直线b相交于点C.
新课导入
A
B
C
D
O
如果两条直线只有一个公共点,就说这两条直线相交.
该公共点叫做两直线的交点,直线AB、CD相交于点O.
1. 相交指的是同一平面内两条直线的一种位置关系;
2. 两条直线相交有且只有一个交点.
注意
新课导入
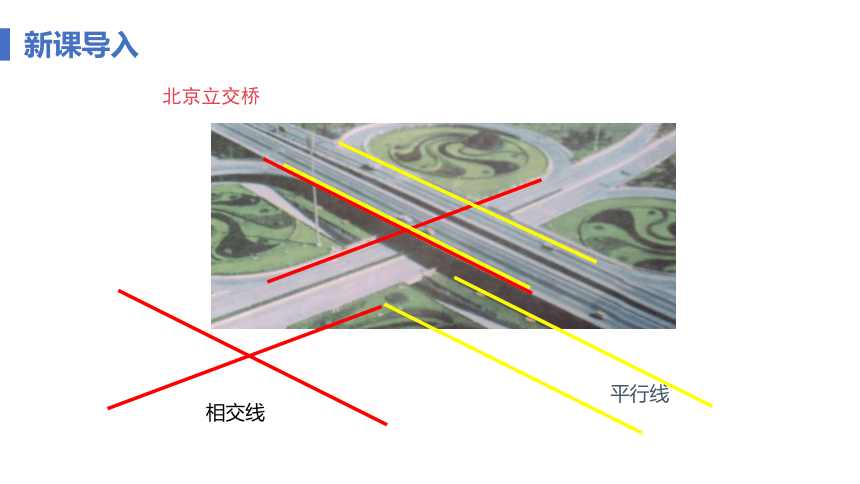
北京立交桥
相交线
平行线
新课讲解
知识点1 邻补角与对顶角的概念
【问题】如图,取两根木条a,b,将它们钉在一起,并把它们想象成两条直线,就得到一个相交线的模型. 在转动木条的过程中,它们所成的角也在变化,你能发现这些角之间不变的关系吗?
新课讲解
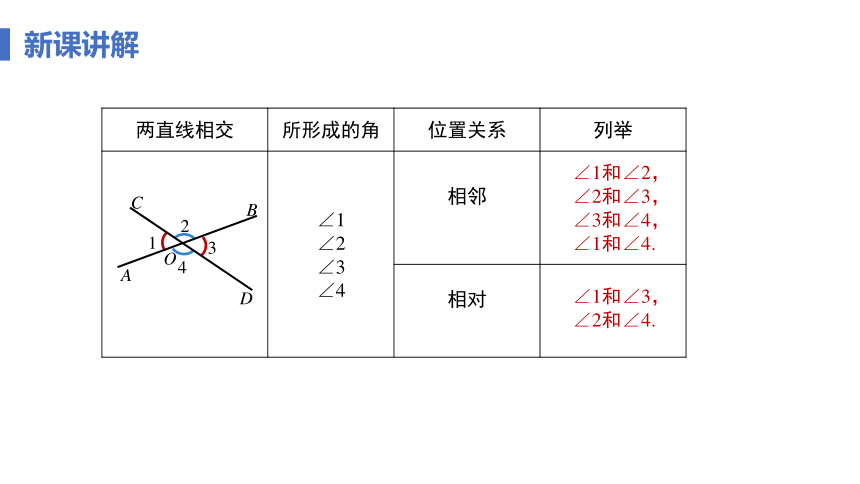
两直线相交 所形成的角 位置关系 列举
∠1 ∠2 ∠3 ∠4 相邻
相对
∠1和∠3,
∠2和∠4.
∠1和∠2,
∠2和∠3,∠3和∠4,
∠1和∠4.
O
B
A
D
C
2
4
1
3
新课讲解
A
O
C
B
D
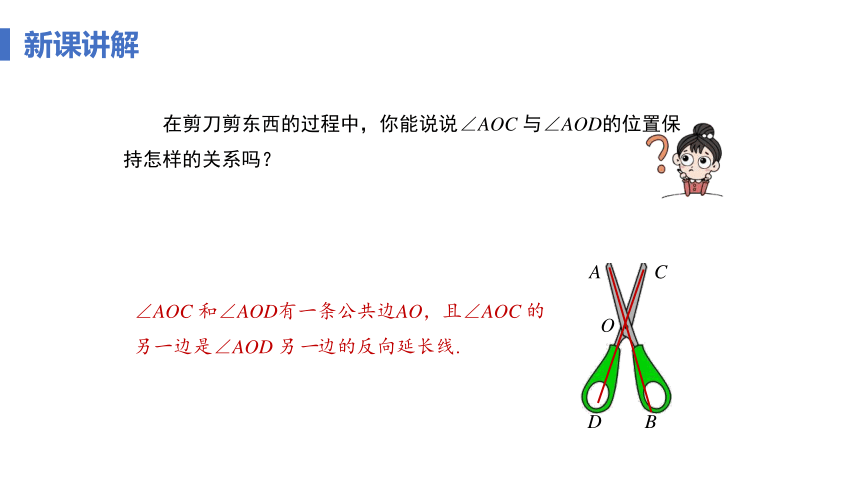
∠AOC 和∠AOD有一条公共边AO,且∠AOC 的另一边是∠AOD 另一边的反向延长线.
在剪刀剪东西的过程中,你能说说∠AOC 与∠AOD的位置保持怎样的关系吗?
新课讲解
O
B
A
D
C
2
4
1
3
∠1和∠2有一条公共边OC,它们的另一边互为反向延长线(∠1和∠2互补),具有这种位置关系的两个角,互为邻补角.
类似的还有:
∠2和∠3,∠3和∠4,∠1和∠4.
图中还有没有其他邻补角?
新课讲解
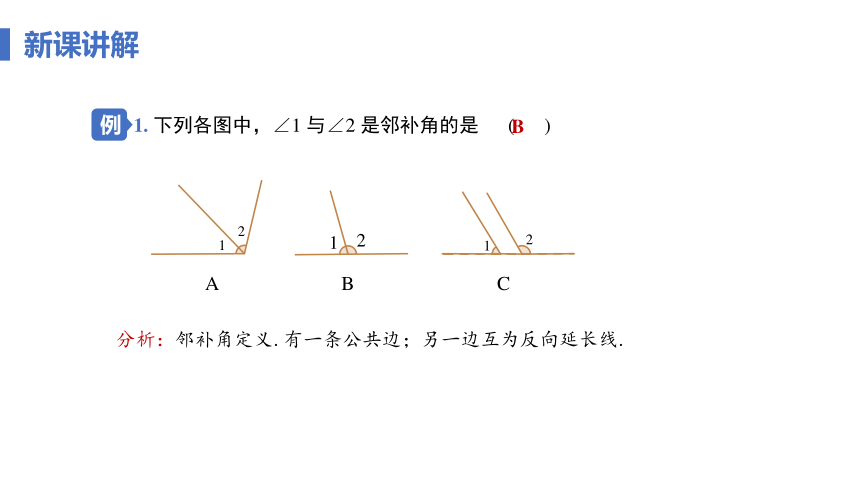
例
1. 下列各图中,∠1 与∠2 是邻补角的是 ( )
B
A B C
分析:邻补角定义.有一条公共边;另一边互为反向延长线.
新课讲解
互为邻补角的“两要素”
1. 有一条公共边;
2. 它们的另一边互为反向延长线.
归纳
1. 邻补角是成对出现的,单独一个角不能称为邻补角.邻补角定义中既指明了位置关系,又指明了数量关系.
2. “邻”指的是位置相邻,即两个角有一条公共边,“补”指的是两个角的数量关系是互补.
注意
新课讲解
练一练
1. 下列图形中,∠1与∠2互为邻补角的是( )
D
分析:判断两个角是否互为邻补角,首先观察两个角是否有公共边,再看另外一条边是否互为反向延长线.
新课讲解
∠1和∠3有一个公共顶点O,并且∠1的两边分别是∠3的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
O
B
A
D
C
2
4
1
3
类似的还有:
∠2和∠4.
图中还有没有其他对顶角?
新课讲解
例
2. 下列各图中,∠1 与∠2 是对顶角的是 ( )
D
A B C D
分析:对顶角定义.一个公共顶点;一个角的两边是另一个角的两边的反向延长线.
新课讲解
对顶角的“两要素”
1. 顶点相同;
2. 角的两边互为反向延长线.
归纳
对顶角是成对出现的,指两个角之间的位置关系,一个角的对顶角只有一个.
注意
新课讲解
练一练
2. 下列图形中,∠1和∠2互为对顶角的是( )
分析:判断两个角是否互为对顶角,首先看两个角有没有公共顶点,再看这两个角的两边是否互为反向延长线.
C
新课讲解
知识点2 邻补角与对顶角的性质
【思考】紧握剪刀的把手去剪纸,就能剪开纸片,在此过程中,剪刀的张角发生了改变,而在改变过程中又有什么是不变的呢?
A
O
C
B
D
∠1 = ∠3
∠1 + ∠2 =180°
如何验证?
新课讲解
【方法一】量角器测量各个角的度数:
∠1 ∠2 ∠3 ∠4
【方法二】几何推导证明:
因为 ∠1 与∠2 互补,∠3 与∠2 互补(补角的定义),
所以 ∠1=∠3 (同角的补角相等).
邻补角互补,对顶角相等.
结论
新课讲解
邻补角与补角的区别:
1. 互为邻补角是互为补角的特殊情况. 互为邻补角的两个角除具备两角互补这一数量关系外,还要具备两角相邻的位置关系.
2. 一个角的邻补角有两个,但一个角的补角可以有多个.
注意:
1. 两个角互为对顶角,它们一定相等;
2. 相等的两个角不一定是对顶角.
新课讲解
例
3. 如图所示,直线 a,b 相交,∠1 = 40°,求∠2,∠3,∠4 的度数.
解:由邻补角的定义,得 ∠2 = 180°-∠1 =180°- 40°= 140°;
由对顶角相等,得∠3 =∠1 =40°,∠4 =∠2 = 140°.
思路点拨:几何中角度的计算,常常找未知角和已知角的关系,通过列方程或简单计算求解.
新课讲解
练一练
1. 如图,直线AB,CD相交于点O,射线OM平分∠BOD,若∠AOC=42°,则∠AOM等于( )
A.159° B.161°
C.169° D.138°
A
∠AOC=42°
∠BOD=42°
∠BOM=21°
∠AOM=159°
解析:
新课讲解
练一练
2. 如图,直线AB,CD 相交于点O,OA 平分∠EOC.若∠EOA:∠EOD=1:3,求∠BOD 的度数.
解:因为∠EOA:∠EOD =1:3,
所以设∠EOA =x°,∠EOD =3x°.
因为OA平分∠EOC,
所以∠COA=∠EOA =x°,∠EOC=2x°.
因为∠EOC+∠EOD =180°(邻补角的定义),
所以2x+3x=180,解得x=36.
所以∠COA =36°.
所以∠BOD =∠COA =36°(对顶角相等).
新课讲解
归纳
角的名称 特征 性质 相同点 不同点
对顶角 ①两条直线相交而成的角 ②有一个公共顶点 ③没有公共边 对顶角相等 都是两直线相交而成的角,都有一个公共顶点,它们都是成对出现. 对顶角没有公共边而邻补角有一条公共边;
两条直线相交时,一个角的对顶角有一个,而一个角的邻补角有两个.
邻补角 ①两条直线相交而成的角 ②有一个公共顶点 ③有一条公共边 邻补角互补
课堂小结
邻补角互补
对顶角相等
对顶角
邻补角
两条直线相交
定义
性质
定义
性质
有一条公共边且另一边互为反向延长线
一个公共顶点且一个角的两边是另一个角的两边的反向延长线
当堂小练
1. 下列说法正确的是 ( )
A. 互补的两个角是邻补角
B. 相等的角是对顶角
C. 有公共边的两个角互为邻补角
D. 两边互为反向延长线的角是对顶角
D
当堂小练
2. 如图,下列各组角中,互为对顶角的是( )
A. ∠1和∠2
B. ∠1和∠3
C. ∠2和∠4
D. ∠2和∠5
A
当堂小练
3. 如图,直线 AB,CD 相交于点O,则∠1的对顶角是( )
A.∠2 B.∠3 C.∠4 D.∠3和∠4
A
当堂小练
4. 如图,直线AB,CD 相交于点O,若∠AOD 减小30°则∠BOC( )
A.增大30° B.增大150° C.不变 D.减小30°
D
当堂小练
5. 如图,直线a,b相交.
(1)∠1+∠2=_________°;∠3+∠4=_______°.
(2)∠4的邻补角是______________.
(3)图中的邻补角共有_____对.
180
180
∠1和∠3
4
当堂小练
6. 如图,直线AB,CD相交于点O,∠AOC:∠BOC=2:7,
则∠AOC=______,∠AOD=_______.
O
B
A
D
C
40°
140°
解:设∠AOC的度数为2x,则∠BOC的度数为7x.
由题意得2x+ 7x=180°,
解得x=20°.
所以∠AOC =2×20°=40°.
∠AOD=∠BOC =7×20°=140°. (对顶角相等)
当堂小练
7. 如图,把一张长方形的纸片按如图所示的方式折叠后,B,D两点分别落在B',D'处.若∠AOB'=80°,则∠B'OG的度数是多少?
解:因为∠AOB'+∠B'OB=180°,∠AOB'=80°,
所以∠B'OB=180°-∠AOB'=180°- 80°=100°.
由折叠可得∠BOG=∠B'OG,
所以∠B'OG= ∠B'OB=×100°=50°.
当堂小练
8. 如图,直线 AB、CD 相交于点 O,OE 是一条射线,∠1:∠3 = 2:7,∠2 = 70°.
(1) 求 ∠1 的度数;
(2) 试说明 OE 平分 ∠COB.
解:(1) 因为∠1:∠3 = 2:7,∠1 + ∠3 = 180°,
所以∠1 = 180°× = 40°.
(2)因为 ∠1+∠2+∠COE = 180°,∠2 = 70°,
所以 ∠COE = 180° -∠1-∠2 = 70°,
所以 ∠2 = ∠COE ,
所以 OE 平分 ∠COB .
当堂小练
9. 如图是一块弯折的屏风,假设其背面不可到达,要测量其在地面上形成的∠AOB的度数,你有什么方法
解:方法1:如图①,延长A0至点C,测量出∠BOC的度数.
因为邻补角互补,所以∠AOB+∠BOC=180°,
所以∠AOB=180°-∠BOC,即可得到∠AOB的度数.
方法2:如图②,延长AO至点C,延长BO至点D,测量出∠COD的度数.
因为对顶角相等,所以∠AOB=∠COD,
即可得到∠AOB的度数.
在生活中,有些角不能直接测量时,可以利用邻补角或对顶角的性质将不能直接测量的角转化为易于测量的角.
方法点拨
当堂小练
10. 观察下列图形,阅读下面的相关文字并回答后面的问题:
4条直线相交,
最多有6个交点
2条直线相交,
只有1个交点
3条直线相交,
最多有3个交点
(1)5条直线相交,最多有几个交点
(2)6条直线相交,最多有几个交点
(3)猜想:n条直线相交,最多有多少个交点
= 10(个).
= 15(个).
个交点.
当堂小练
11. 如图,三条直线 l1 ,l2,l3 相交于一点,则∠1+∠2+∠3 等于( )
A.90° B.120° C.180° D.360°
C
3
1
2
l1
l2
l3
对接中考
60
1. 如图,AB 与 CD 相交于点 O,OE 是 ∠AOC 的平分线,且 OC 恰好平分 ∠EOB,则∠AOD = 度.
O
A
C
B
D
E
∠AOE=∠COE,∠COE=∠BOC
∠AOE=∠COE=∠BOC=60°
∠AOD=∠BOC=60°
对接中考
190
2. 如图,3 条直线两两相交最多有 3 个交点,4 条直线两两相交最多有 6 个交点,按照这样的规律,则 20 条直线两两相交最多有 个交点.
1+2=3
1+2+3=6
n 条直线相交,交点个数最多是 1+2+3+…+(n-1)= .
当 n=20 时,交点个数最多是 .
对接中考
3. 如图,直线a,b相交于点O,如果∠ 1+ ∠ 2=60°,那么∠ 3 是( )
A. 150°
B. 120°
C. 60°
D. 30°
A
拓展与延伸
1.如图,点O是直线AB上的任意一点,OC,OD,OE是过点O的三条射线,若∠AOD=∠COE=90°,则下列说法:
①与∠AOC互为邻补角的角只有一个;
②与∠AOC互为补角的角只有一个;
③与∠AOC互为邻补角的角有两个;
④与∠AOC互为补角的角有两个.
其中正确的是( )
A.②③ B.①②
C.③④ D.①④
D
拓展与延伸
2.如图,两条直线 a,b 相交.
(1) 如果 ∠1=50°,求 ∠2,∠3 的度数;
(2) 如果 ∠2=3∠1,求 ∠3,∠4 的度数.
解:(1)∵∠1=50°,∠1+∠2=180°,
∴∠2=180°-50°=130°,
又∵∠3与∠1是对顶角,
∴∠3=∠1=50°.
1
2
3
4
a
b
(2)∵∠2=3∠1,∠1+∠2=180°,
∴∠1+3∠1=180°,
∴4∠1=180°,∴∠1=45°,
∴∠3=∠1=45°,
又∵∠1+∠4=180°,
∴∠4=180°-∠1=180°-45°=135°.
第七章 相交线与平行线
7.1 相交线
7.1.1 两条直线相交
目
录
1. 学习目标
4. 知识点1 邻补角与对顶角的概念
6. 课堂小结
7. 当堂小练
CONTENTS
3. 新课导入
5. 知识点2 邻补角与对顶角的性质
9. 拓展与延伸
2. 知识回顾
8. 对接中考
1. 理解两条直线相交的特征及邻补角与对顶角的概念.
2. 掌握对顶角相等的性质.
3. 运用对顶角与邻补角的性质进行有关的推理或计算.
学习目标
知识回顾
如果两个角的和等于90°(直角),就说这两个角互为余角
余角和补角
定义
性质
同角(等角)的余角相等
补角
如果两个角的和等于180°(平角),就说这两个角互为补角
定义
性质
同角(等角)的补角相等
余角
新课导入
【复习】用适当的语句表述图中点与直线的关系.
解:如图 ,直线a,b,c两两相交,
直线b与直线c相交于点A,
直线a与直线c相交于点B,
直线a与直线b相交于点C.
新课导入
A
B
C
D
O
如果两条直线只有一个公共点,就说这两条直线相交.
该公共点叫做两直线的交点,直线AB、CD相交于点O.
1. 相交指的是同一平面内两条直线的一种位置关系;
2. 两条直线相交有且只有一个交点.
注意
新课导入
北京立交桥
相交线
平行线
新课讲解
知识点1 邻补角与对顶角的概念
【问题】如图,取两根木条a,b,将它们钉在一起,并把它们想象成两条直线,就得到一个相交线的模型. 在转动木条的过程中,它们所成的角也在变化,你能发现这些角之间不变的关系吗?
新课讲解
两直线相交 所形成的角 位置关系 列举
∠1 ∠2 ∠3 ∠4 相邻
相对
∠1和∠3,
∠2和∠4.
∠1和∠2,
∠2和∠3,∠3和∠4,
∠1和∠4.
O
B
A
D
C
2
4
1
3
新课讲解
A
O
C
B
D
∠AOC 和∠AOD有一条公共边AO,且∠AOC 的另一边是∠AOD 另一边的反向延长线.
在剪刀剪东西的过程中,你能说说∠AOC 与∠AOD的位置保持怎样的关系吗?
新课讲解
O
B
A
D
C
2
4
1
3
∠1和∠2有一条公共边OC,它们的另一边互为反向延长线(∠1和∠2互补),具有这种位置关系的两个角,互为邻补角.
类似的还有:
∠2和∠3,∠3和∠4,∠1和∠4.
图中还有没有其他邻补角?
新课讲解
例
1. 下列各图中,∠1 与∠2 是邻补角的是 ( )
B
A B C
分析:邻补角定义.有一条公共边;另一边互为反向延长线.
新课讲解
互为邻补角的“两要素”
1. 有一条公共边;
2. 它们的另一边互为反向延长线.
归纳
1. 邻补角是成对出现的,单独一个角不能称为邻补角.邻补角定义中既指明了位置关系,又指明了数量关系.
2. “邻”指的是位置相邻,即两个角有一条公共边,“补”指的是两个角的数量关系是互补.
注意
新课讲解
练一练
1. 下列图形中,∠1与∠2互为邻补角的是( )
D
分析:判断两个角是否互为邻补角,首先观察两个角是否有公共边,再看另外一条边是否互为反向延长线.
新课讲解
∠1和∠3有一个公共顶点O,并且∠1的两边分别是∠3的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
O
B
A
D
C
2
4
1
3
类似的还有:
∠2和∠4.
图中还有没有其他对顶角?
新课讲解
例
2. 下列各图中,∠1 与∠2 是对顶角的是 ( )
D
A B C D
分析:对顶角定义.一个公共顶点;一个角的两边是另一个角的两边的反向延长线.
新课讲解
对顶角的“两要素”
1. 顶点相同;
2. 角的两边互为反向延长线.
归纳
对顶角是成对出现的,指两个角之间的位置关系,一个角的对顶角只有一个.
注意
新课讲解
练一练
2. 下列图形中,∠1和∠2互为对顶角的是( )
分析:判断两个角是否互为对顶角,首先看两个角有没有公共顶点,再看这两个角的两边是否互为反向延长线.
C
新课讲解
知识点2 邻补角与对顶角的性质
【思考】紧握剪刀的把手去剪纸,就能剪开纸片,在此过程中,剪刀的张角发生了改变,而在改变过程中又有什么是不变的呢?
A
O
C
B
D
∠1 = ∠3
∠1 + ∠2 =180°
如何验证?
新课讲解
【方法一】量角器测量各个角的度数:
∠1 ∠2 ∠3 ∠4
【方法二】几何推导证明:
因为 ∠1 与∠2 互补,∠3 与∠2 互补(补角的定义),
所以 ∠1=∠3 (同角的补角相等).
邻补角互补,对顶角相等.
结论
新课讲解
邻补角与补角的区别:
1. 互为邻补角是互为补角的特殊情况. 互为邻补角的两个角除具备两角互补这一数量关系外,还要具备两角相邻的位置关系.
2. 一个角的邻补角有两个,但一个角的补角可以有多个.
注意:
1. 两个角互为对顶角,它们一定相等;
2. 相等的两个角不一定是对顶角.
新课讲解
例
3. 如图所示,直线 a,b 相交,∠1 = 40°,求∠2,∠3,∠4 的度数.
解:由邻补角的定义,得 ∠2 = 180°-∠1 =180°- 40°= 140°;
由对顶角相等,得∠3 =∠1 =40°,∠4 =∠2 = 140°.
思路点拨:几何中角度的计算,常常找未知角和已知角的关系,通过列方程或简单计算求解.
新课讲解
练一练
1. 如图,直线AB,CD相交于点O,射线OM平分∠BOD,若∠AOC=42°,则∠AOM等于( )
A.159° B.161°
C.169° D.138°
A
∠AOC=42°
∠BOD=42°
∠BOM=21°
∠AOM=159°
解析:
新课讲解
练一练
2. 如图,直线AB,CD 相交于点O,OA 平分∠EOC.若∠EOA:∠EOD=1:3,求∠BOD 的度数.
解:因为∠EOA:∠EOD =1:3,
所以设∠EOA =x°,∠EOD =3x°.
因为OA平分∠EOC,
所以∠COA=∠EOA =x°,∠EOC=2x°.
因为∠EOC+∠EOD =180°(邻补角的定义),
所以2x+3x=180,解得x=36.
所以∠COA =36°.
所以∠BOD =∠COA =36°(对顶角相等).
新课讲解
归纳
角的名称 特征 性质 相同点 不同点
对顶角 ①两条直线相交而成的角 ②有一个公共顶点 ③没有公共边 对顶角相等 都是两直线相交而成的角,都有一个公共顶点,它们都是成对出现. 对顶角没有公共边而邻补角有一条公共边;
两条直线相交时,一个角的对顶角有一个,而一个角的邻补角有两个.
邻补角 ①两条直线相交而成的角 ②有一个公共顶点 ③有一条公共边 邻补角互补
课堂小结
邻补角互补
对顶角相等
对顶角
邻补角
两条直线相交
定义
性质
定义
性质
有一条公共边且另一边互为反向延长线
一个公共顶点且一个角的两边是另一个角的两边的反向延长线
当堂小练
1. 下列说法正确的是 ( )
A. 互补的两个角是邻补角
B. 相等的角是对顶角
C. 有公共边的两个角互为邻补角
D. 两边互为反向延长线的角是对顶角
D
当堂小练
2. 如图,下列各组角中,互为对顶角的是( )
A. ∠1和∠2
B. ∠1和∠3
C. ∠2和∠4
D. ∠2和∠5
A
当堂小练
3. 如图,直线 AB,CD 相交于点O,则∠1的对顶角是( )
A.∠2 B.∠3 C.∠4 D.∠3和∠4
A
当堂小练
4. 如图,直线AB,CD 相交于点O,若∠AOD 减小30°则∠BOC( )
A.增大30° B.增大150° C.不变 D.减小30°
D
当堂小练
5. 如图,直线a,b相交.
(1)∠1+∠2=_________°;∠3+∠4=_______°.
(2)∠4的邻补角是______________.
(3)图中的邻补角共有_____对.
180
180
∠1和∠3
4
当堂小练
6. 如图,直线AB,CD相交于点O,∠AOC:∠BOC=2:7,
则∠AOC=______,∠AOD=_______.
O
B
A
D
C
40°
140°
解:设∠AOC的度数为2x,则∠BOC的度数为7x.
由题意得2x+ 7x=180°,
解得x=20°.
所以∠AOC =2×20°=40°.
∠AOD=∠BOC =7×20°=140°. (对顶角相等)
当堂小练
7. 如图,把一张长方形的纸片按如图所示的方式折叠后,B,D两点分别落在B',D'处.若∠AOB'=80°,则∠B'OG的度数是多少?
解:因为∠AOB'+∠B'OB=180°,∠AOB'=80°,
所以∠B'OB=180°-∠AOB'=180°- 80°=100°.
由折叠可得∠BOG=∠B'OG,
所以∠B'OG= ∠B'OB=×100°=50°.
当堂小练
8. 如图,直线 AB、CD 相交于点 O,OE 是一条射线,∠1:∠3 = 2:7,∠2 = 70°.
(1) 求 ∠1 的度数;
(2) 试说明 OE 平分 ∠COB.
解:(1) 因为∠1:∠3 = 2:7,∠1 + ∠3 = 180°,
所以∠1 = 180°× = 40°.
(2)因为 ∠1+∠2+∠COE = 180°,∠2 = 70°,
所以 ∠COE = 180° -∠1-∠2 = 70°,
所以 ∠2 = ∠COE ,
所以 OE 平分 ∠COB .
当堂小练
9. 如图是一块弯折的屏风,假设其背面不可到达,要测量其在地面上形成的∠AOB的度数,你有什么方法
解:方法1:如图①,延长A0至点C,测量出∠BOC的度数.
因为邻补角互补,所以∠AOB+∠BOC=180°,
所以∠AOB=180°-∠BOC,即可得到∠AOB的度数.
方法2:如图②,延长AO至点C,延长BO至点D,测量出∠COD的度数.
因为对顶角相等,所以∠AOB=∠COD,
即可得到∠AOB的度数.
在生活中,有些角不能直接测量时,可以利用邻补角或对顶角的性质将不能直接测量的角转化为易于测量的角.
方法点拨
当堂小练
10. 观察下列图形,阅读下面的相关文字并回答后面的问题:
4条直线相交,
最多有6个交点
2条直线相交,
只有1个交点
3条直线相交,
最多有3个交点
(1)5条直线相交,最多有几个交点
(2)6条直线相交,最多有几个交点
(3)猜想:n条直线相交,最多有多少个交点
= 10(个).
= 15(个).
个交点.
当堂小练
11. 如图,三条直线 l1 ,l2,l3 相交于一点,则∠1+∠2+∠3 等于( )
A.90° B.120° C.180° D.360°
C
3
1
2
l1
l2
l3
对接中考
60
1. 如图,AB 与 CD 相交于点 O,OE 是 ∠AOC 的平分线,且 OC 恰好平分 ∠EOB,则∠AOD = 度.
O
A
C
B
D
E
∠AOE=∠COE,∠COE=∠BOC
∠AOE=∠COE=∠BOC=60°
∠AOD=∠BOC=60°
对接中考
190
2. 如图,3 条直线两两相交最多有 3 个交点,4 条直线两两相交最多有 6 个交点,按照这样的规律,则 20 条直线两两相交最多有 个交点.
1+2=3
1+2+3=6
n 条直线相交,交点个数最多是 1+2+3+…+(n-1)= .
当 n=20 时,交点个数最多是 .
对接中考
3. 如图,直线a,b相交于点O,如果∠ 1+ ∠ 2=60°,那么∠ 3 是( )
A. 150°
B. 120°
C. 60°
D. 30°
A
拓展与延伸
1.如图,点O是直线AB上的任意一点,OC,OD,OE是过点O的三条射线,若∠AOD=∠COE=90°,则下列说法:
①与∠AOC互为邻补角的角只有一个;
②与∠AOC互为补角的角只有一个;
③与∠AOC互为邻补角的角有两个;
④与∠AOC互为补角的角有两个.
其中正确的是( )
A.②③ B.①②
C.③④ D.①④
D
拓展与延伸
2.如图,两条直线 a,b 相交.
(1) 如果 ∠1=50°,求 ∠2,∠3 的度数;
(2) 如果 ∠2=3∠1,求 ∠3,∠4 的度数.
解:(1)∵∠1=50°,∠1+∠2=180°,
∴∠2=180°-50°=130°,
又∵∠3与∠1是对顶角,
∴∠3=∠1=50°.
1
2
3
4
a
b
(2)∵∠2=3∠1,∠1+∠2=180°,
∴∠1+3∠1=180°,
∴4∠1=180°,∴∠1=45°,
∴∠3=∠1=45°,
又∵∠1+∠4=180°,
∴∠4=180°-∠1=180°-45°=135°.
同课章节目录
