5.4.2 圆周角定理的推论3(学案带答案)
文档属性
| 名称 | 5.4.2 圆周角定理的推论3(学案带答案) |  | |
| 格式 | docx | ||
| 文件大小 | 23.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-13 07:55:20 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
5.4.2 圆周角定理的推论3(学案带答案)
列清单·划重点
知识点1 圆周角定理的推论3
直径所对的圆周角是__________;90°的圆周角所对的弦是________.
符号语言:
①∵AB 是⊙O的直径,∴∠ACB=90°.
②∵∠ACB=90°,∴AB 是⊙O的直径.
知识点2 在解答与圆的直径有关的问题时,常添加的辅助线
如图所示,在解答与圆的直径有关的问题时,常常利用直径所对的圆周角是直角这一性质.有时还需要添加辅助线,构成直径所对的圆周角,以便转化为直角三角形的问题去研究.
明考点·识方法
考点1 与圆周角定理的推论3有关的计算题
典例 1 AB为半圆O的直径,点C 为半 圆上 一点,且∠CAB=50°.①以点 B为圆心,适当长为半径作弧,交AB,BC 于D,E;②分别以D,E为圆心,大于 为半径作弧,两弧交于点 P;③作射线 BP.则∠ABP= ( )
A. 40° B. 25° C. 20° D. 15°
思路导析 根据直径所对的圆周角是 90°得出∠ACB的度数,再由∠CAB=50°得出∠ABC 的度数,最后根据所画射线为∠ABC 的角平分线即可解决问题.
变式1 如图所示,小华同学设计了一个圆直径的测量器,标有刻度的尺子OA,OB 在O点钉在一起,并使它们保持垂直.在测直径时,把O 点靠在圆周上,读得刻度 8个单位,OF=6个单位,则圆的直径为 ( )
A.12个单位 B.10个单位 C.4个单位 D.15个单位
变式 1图 变式2图
变式2 如图所示,AD是⊙O的直径,弦BC交AD 于点 E,连接 AB,AC,若∠BAD=30°,则∠ACB 的度数是 ( )
A. 50° B. 40° C. 70° D. 60°
考点2 与圆周角定理的推论3有关的证明题
典例 2 如图所示,AB 为⊙O 的直径,AB=AC,BC交⊙O 于点 D,AC 交⊙O于点E, ∠BAC=45°.
(1)求∠EBC的度数;
(2)求证:BD=CD.
思路导析 (1)利用圆周角定理的推论3,根据以及等腰三角形的性质进行求解即可;(2)由AB是⊙O的直径,连接AD,构造圆周角∠ADB是直角,进而利用等腰三角形的性质证明即可.
规律总结
在解决圆的有关问题时,遇到圆的直径常常要添加辅助线,构成直径所对的圆周角,以便利用直径所对的圆周角是直角这一性质.
变式 如图,以 的边AC 为直径作⊙O,交 BC边于点 D,过点 C 作CE∥AB 交⊙O于点 E,连接 AD,DE,∠B=∠ADE.
(1)求证:AC=BC;
(2)若tanB=2,CD=3,求AB 和DE 的长.
当堂测·夯基础
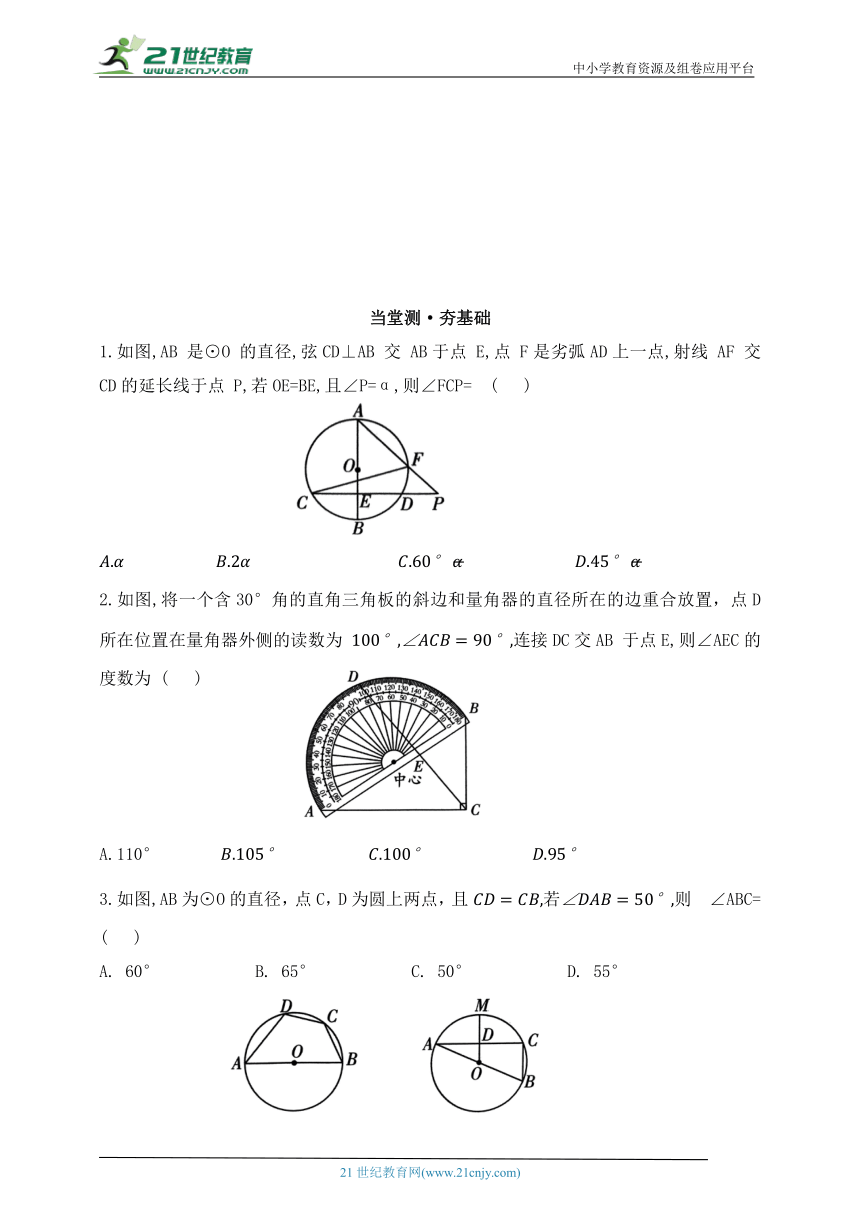
1.如图,AB 是⊙O 的直径,弦CD⊥AB 交 AB于点 E,点 F是劣弧AD上一点,射线 AF 交 CD的延长线于点 P,若OE=BE,且∠P=α,则∠FCP= ( )
2.如图,将一个含30°角的直角三角板的斜边和量角器的直径所在的边重合放置,点D 所在位置在量角器外侧的读数为 连接DC交AB 于点E,则∠AEC的度数为 ( )
A.110°
3.如图,AB为⊙O的直径,点C,D为圆上两点,且若则 ∠ABC= ( )
A. 60° B. 65° C. 50° D. 55°
第3题图 第4题图
4.如图,AB 是⊙O的直径,点 D,M分别是弦 AC,弧AC的中点, 12,BC=5,则 MD的长是__________.
5.如图,在锐角中,AC是最短边.以AC 为直径的⊙O,交 BC 于 D,过O作 ∥交⊙O于E,连接AD,AE,CE.
(1)求证:
(2)若 求 的度数;
(3)若 求 CF的长.
参考答案
【列清单·划重点】
知识点1 直角 直径
【明考点·识方法】
典例1 C 解析:∵AB为半圆O的直径,∴∠ACB=90°,
又∵∠CAB=50°,∴∠ABC=40°.
根据作图步骤可知,BP 平分∠ABC,
变式1 B 变式2 D
典例2 解:(1)∵AB是⊙O的直径,∴∠AEB=∠BEC=90°.
∵AB=AC,∠BAC=45°,
∴∠EBC=90°-67.5°=22.5°;
(2)证明:如图所示,连接AD.
∵AB是⊙O的直径,∴∠ADB=90°,即AD⊥BC.
又∵AB=AC,∴BD=CD.
变式 解:(1)证明:∵∠ADE=∠ACE,∠ADE=∠B,∴∠B=∠ACE,
∵CE∥AB,∴∠BAC=∠ACE,∴∠B=∠BAC,∴AC=BC;
(2)如图,连接AE,
∵∠ADE=∠B,∠AED=∠ACB,∴△ADE∽△ABC,
∵AC为⊙O的直径,∴∠ADB=∠ADC=90°,∴AD=2BD,
∵CD=3,∴AC=BC=BD+CD=BD+3,
解得 BD=2或BD=0(舍去),
【当堂测·夯基础】
1. C 2. C 3. B 4. 4
5.解:(1)证明:∵OC=OE,∴∠OEC=∠OCE,
∵OE∥BC,∴∠OEC=∠ECD,
∴∠OCE=∠ECD,即∠ACE=∠DCE;
(2)延长AE交 BC 于点G,
∵∠AGC 是△ABG的外角,∴∠AGC=∠B+∠BAG=60°,
∵OE∥BC,∴∠AEO=∠AGC=60°,∵OA=OE,∴∠EAO=∠AEO=60°;
(3)∵O是AC 中点,
∵AC是直径,∴∠AEC=∠FDC=90°,
∵∠ACE=∠FCD,∴△CDF∽△CEA,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
5.4.2 圆周角定理的推论3(学案带答案)
列清单·划重点
知识点1 圆周角定理的推论3
直径所对的圆周角是__________;90°的圆周角所对的弦是________.
符号语言:
①∵AB 是⊙O的直径,∴∠ACB=90°.
②∵∠ACB=90°,∴AB 是⊙O的直径.
知识点2 在解答与圆的直径有关的问题时,常添加的辅助线
如图所示,在解答与圆的直径有关的问题时,常常利用直径所对的圆周角是直角这一性质.有时还需要添加辅助线,构成直径所对的圆周角,以便转化为直角三角形的问题去研究.
明考点·识方法
考点1 与圆周角定理的推论3有关的计算题
典例 1 AB为半圆O的直径,点C 为半 圆上 一点,且∠CAB=50°.①以点 B为圆心,适当长为半径作弧,交AB,BC 于D,E;②分别以D,E为圆心,大于 为半径作弧,两弧交于点 P;③作射线 BP.则∠ABP= ( )
A. 40° B. 25° C. 20° D. 15°
思路导析 根据直径所对的圆周角是 90°得出∠ACB的度数,再由∠CAB=50°得出∠ABC 的度数,最后根据所画射线为∠ABC 的角平分线即可解决问题.
变式1 如图所示,小华同学设计了一个圆直径的测量器,标有刻度的尺子OA,OB 在O点钉在一起,并使它们保持垂直.在测直径时,把O 点靠在圆周上,读得刻度 8个单位,OF=6个单位,则圆的直径为 ( )
A.12个单位 B.10个单位 C.4个单位 D.15个单位
变式 1图 变式2图
变式2 如图所示,AD是⊙O的直径,弦BC交AD 于点 E,连接 AB,AC,若∠BAD=30°,则∠ACB 的度数是 ( )
A. 50° B. 40° C. 70° D. 60°
考点2 与圆周角定理的推论3有关的证明题
典例 2 如图所示,AB 为⊙O 的直径,AB=AC,BC交⊙O 于点 D,AC 交⊙O于点E, ∠BAC=45°.
(1)求∠EBC的度数;
(2)求证:BD=CD.
思路导析 (1)利用圆周角定理的推论3,根据以及等腰三角形的性质进行求解即可;(2)由AB是⊙O的直径,连接AD,构造圆周角∠ADB是直角,进而利用等腰三角形的性质证明即可.
规律总结
在解决圆的有关问题时,遇到圆的直径常常要添加辅助线,构成直径所对的圆周角,以便利用直径所对的圆周角是直角这一性质.
变式 如图,以 的边AC 为直径作⊙O,交 BC边于点 D,过点 C 作CE∥AB 交⊙O于点 E,连接 AD,DE,∠B=∠ADE.
(1)求证:AC=BC;
(2)若tanB=2,CD=3,求AB 和DE 的长.
当堂测·夯基础
1.如图,AB 是⊙O 的直径,弦CD⊥AB 交 AB于点 E,点 F是劣弧AD上一点,射线 AF 交 CD的延长线于点 P,若OE=BE,且∠P=α,则∠FCP= ( )
2.如图,将一个含30°角的直角三角板的斜边和量角器的直径所在的边重合放置,点D 所在位置在量角器外侧的读数为 连接DC交AB 于点E,则∠AEC的度数为 ( )
A.110°
3.如图,AB为⊙O的直径,点C,D为圆上两点,且若则 ∠ABC= ( )
A. 60° B. 65° C. 50° D. 55°
第3题图 第4题图
4.如图,AB 是⊙O的直径,点 D,M分别是弦 AC,弧AC的中点, 12,BC=5,则 MD的长是__________.
5.如图,在锐角中,AC是最短边.以AC 为直径的⊙O,交 BC 于 D,过O作 ∥交⊙O于E,连接AD,AE,CE.
(1)求证:
(2)若 求 的度数;
(3)若 求 CF的长.
参考答案
【列清单·划重点】
知识点1 直角 直径
【明考点·识方法】
典例1 C 解析:∵AB为半圆O的直径,∴∠ACB=90°,
又∵∠CAB=50°,∴∠ABC=40°.
根据作图步骤可知,BP 平分∠ABC,
变式1 B 变式2 D
典例2 解:(1)∵AB是⊙O的直径,∴∠AEB=∠BEC=90°.
∵AB=AC,∠BAC=45°,
∴∠EBC=90°-67.5°=22.5°;
(2)证明:如图所示,连接AD.
∵AB是⊙O的直径,∴∠ADB=90°,即AD⊥BC.
又∵AB=AC,∴BD=CD.
变式 解:(1)证明:∵∠ADE=∠ACE,∠ADE=∠B,∴∠B=∠ACE,
∵CE∥AB,∴∠BAC=∠ACE,∴∠B=∠BAC,∴AC=BC;
(2)如图,连接AE,
∵∠ADE=∠B,∠AED=∠ACB,∴△ADE∽△ABC,
∵AC为⊙O的直径,∴∠ADB=∠ADC=90°,∴AD=2BD,
∵CD=3,∴AC=BC=BD+CD=BD+3,
解得 BD=2或BD=0(舍去),
【当堂测·夯基础】
1. C 2. C 3. B 4. 4
5.解:(1)证明:∵OC=OE,∴∠OEC=∠OCE,
∵OE∥BC,∴∠OEC=∠ECD,
∴∠OCE=∠ECD,即∠ACE=∠DCE;
(2)延长AE交 BC 于点G,
∵∠AGC 是△ABG的外角,∴∠AGC=∠B+∠BAG=60°,
∵OE∥BC,∴∠AEO=∠AGC=60°,∵OA=OE,∴∠EAO=∠AEO=60°;
(3)∵O是AC 中点,
∵AC是直径,∴∠AEC=∠FDC=90°,
∵∠ACE=∠FCD,∴△CDF∽△CEA,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
