2.2.1平行四边形的性质(第一课时) 课件(共26张PPT)
文档属性
| 名称 | 2.2.1平行四边形的性质(第一课时) 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-12 21:13:24 | ||
图片预览






文档简介
(共26张PPT)
第一章 直角三角形
2.2.1平行四边形的性质(第一课时)
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
01
02
03
理解平行四边形的概念,掌握平行四边形的性质.
利用平行四边形的性质解决相关问题.
02
新知导入
在图中找出平行四边形
03
新知探究
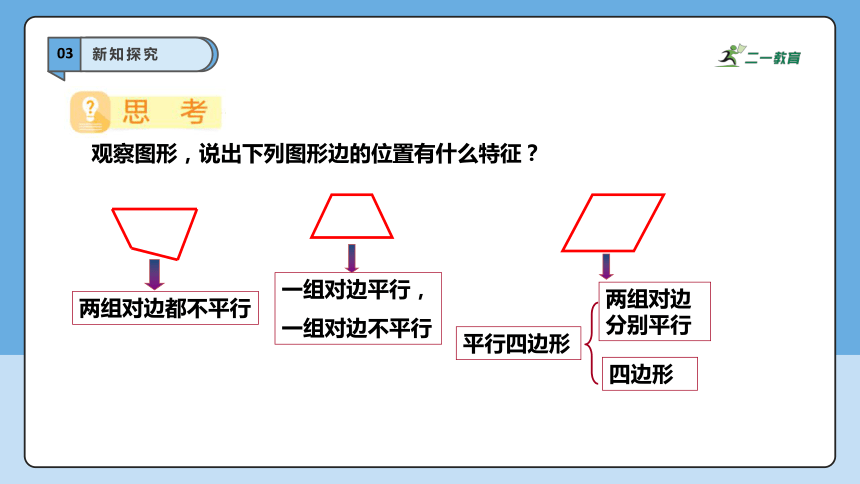
两组对边都不平行
一组对边平行,
一组对边不平行
两组对边分别平行
四边形
平行四边形
观察图形,说出下列图形边的位置有什么特征?
03
新知探究
有两组对边分别平行的四边形叫做平行四边形。
平行四边形的定义
如图:四边形ABCD是平行四边形
记作: ABCD
读作:平行四边形ABCD
AB与CD,AD与BC叫做对边
∠A与∠C,∠B与∠D叫做对角
∠A与∠B,∠C与∠D叫做邻角
03
新知讲解
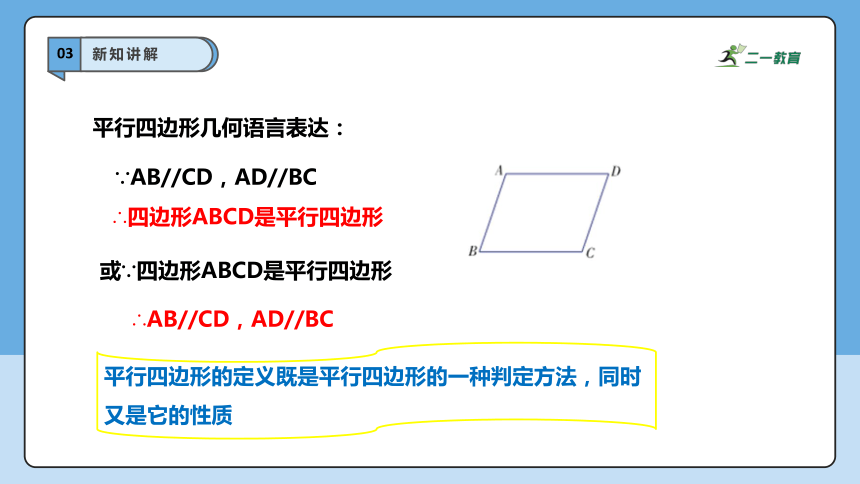
平行四边形几何语言表达:
∵AB//CD,AD//BC
∴四边形ABCD是平行四边形
或∵四边形ABCD是平行四边形
∴AB//CD,AD//BC
平行四边形的定义既是平行四边形的一种判定方法,同时又是它的性质
03
新知讲解
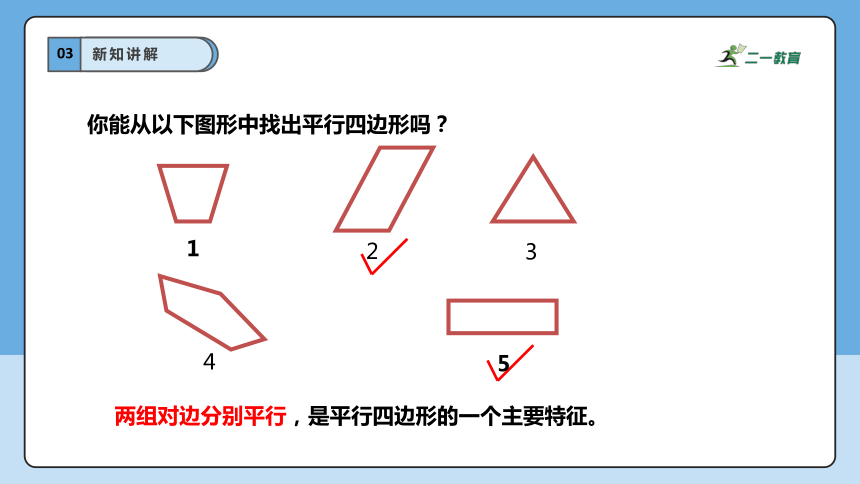
你能从以下图形中找出平行四边形吗?
两组对边分别平行,是平行四边形的一个主要特征。
2
3
1
4
5
03
新知讲解
探究
根据定义画一个平行四边形,请用直尺,量角器测量平行四边形四条边的长度、四个角的大小,由此你能做出什么猜测?
03
新知讲解
AB=DC,AD=BC, ∠A=∠C, ∠B=∠D
你能证明吗?
03
新知讲解
∵ 四边形 ABCD 为平行四边形,
∴ AB ∥ DC, AD ∥ BC (平行四边形的两组对 边分别平行).
∴ ∠1= ∠2, ∠3= ∠4.
又 AC=CA,
∴ △ABC≌△CDA.
∴ AB = CD, BC = DA, ∠B = ∠D. 又 ∠1+ ∠4= ∠2+ ∠3,
∴ ∠BAD = ∠DCB.
如图, 连接 AC.
证明:
03
新知讲解
平行四边形的性质定理:
总结
平行四边形的对边相等, 平行四边形的对角相等.
∵四边形ABCD是平行四边形
几何语言
∴AB=CD,BC=AD.
∴∠A=∠C,∠B=∠D.
A
B
C
D
新课探究
例1
如图, 四边形ABCD和BCEF均为平行四边形,AD=2cm, ∠A=65°,∠E=33°,求EF和∠BGC.
03
新知讲解
解 ∵ 四边形ABCD是平行四边形,
∴ AD=BC=2cm,∠1=∠A=65°.
∵ 四边形BCEF是平行四边形,
∴ EF=BC=2cm,∠2=∠E=33°.
∴ 在△BGC中,∠BGC=180°-∠1-∠2=82°.
03
新知讲解
例2、如图,直线 l1与l2平行,AB,CD是l1与l2之间的任意两条平行线段. 试问:AB与CD是否相等?为什么?
解 ∵ l1∥l2,AB∥CD,
∴ 四边形ABDC是平行四边形.
∴ AB=CD.
结论:
夹在两条平行线间的平行线段相等
03
新知讲解
若a//b,DA、GH、CB垂直于a,交a于A、G、B,交b于D、H、C.
则DA=GH=CB
两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离.
两条平行线之间的距离相等
04
课堂练习
【知识技能类作业】必做题:
1.如图,在□ABCD中,AD=3 cm,AB=2 cm,则□ABCD的周长等于( )
A.10 cm B.6 cm C.5 cm D.4 cm
A
04
课堂练习
【知识技能类作业】选做题:
2.如图,过□ABCD的对角线BD上一点M分别作平行四边形两边的平行线EF与GH,那么图中的□AEMG的面积S1与□HCFM的面积S2的大小关系是( )
A.S1>S2 B.S1C
04
课堂练习
【综合拓展类作业】
3.已知:平行四边形□ABCD的周长为60cm,两邻边AB,BC长的比为3:2,求AB和BC的长度 .
解:∵四边形ABCD是平行四边形(已知)
∴ AB=CD,BC=AD(平行四边形的对边相等)
又∵□ABCD的周长为60cm.
∴AB+BC=30cm.
又AB:BC=3:2,即AB=1.5BC.
则1.5BC+BC=30 , 解得BC=12 (cm).
而AB=1.5×12=18 (cm).
05
课堂小结
平行四边形的性质
3、平行线间的平行线段
有两组对边分别平行的四边形叫做平行四边形。
1、平行四边形的定义
平行四边形的对边相等, 平行四边形的对角相等.
夹在两条平行线间的平行线段相等
2、平行四边形的性质
06
作业布置
【知识技能类作业】必做题:
1、如图,在□ABCD中,BE⊥AD于点E,若∠ABE=50°,则∠C=__________.
40°
06
作业布置
【知识技能类作业】选做题:
2、如图,□ABCD与□DCFE的周长相等,且∠BAD=60°,∠F=110°,则∠DAE的度数为__________.
25°
06
作业布置
【综合拓展类作业】
3、已知:在□ABCD中,AE⊥BC,垂足为点E,CE=CD,点F为CE的中点,点G为CD上的一点,连接DF、EG、AG,若CF=2,AE=3,求BE的长;
06
作业布置
【综合拓展类作业】
解:∵点F为CE的中点,
∴CE=CD=2CF=4.
又∵四边形ABCD为平行四边形,
∴AB=CD=4.
在Rt△ABE中,由勾股定理得BE== .
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第一章 直角三角形
2.2.1平行四边形的性质(第一课时)
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
01
02
03
理解平行四边形的概念,掌握平行四边形的性质.
利用平行四边形的性质解决相关问题.
02
新知导入
在图中找出平行四边形
03
新知探究
两组对边都不平行
一组对边平行,
一组对边不平行
两组对边分别平行
四边形
平行四边形
观察图形,说出下列图形边的位置有什么特征?
03
新知探究
有两组对边分别平行的四边形叫做平行四边形。
平行四边形的定义
如图:四边形ABCD是平行四边形
记作: ABCD
读作:平行四边形ABCD
AB与CD,AD与BC叫做对边
∠A与∠C,∠B与∠D叫做对角
∠A与∠B,∠C与∠D叫做邻角
03
新知讲解
平行四边形几何语言表达:
∵AB//CD,AD//BC
∴四边形ABCD是平行四边形
或∵四边形ABCD是平行四边形
∴AB//CD,AD//BC
平行四边形的定义既是平行四边形的一种判定方法,同时又是它的性质
03
新知讲解
你能从以下图形中找出平行四边形吗?
两组对边分别平行,是平行四边形的一个主要特征。
2
3
1
4
5
03
新知讲解
探究
根据定义画一个平行四边形,请用直尺,量角器测量平行四边形四条边的长度、四个角的大小,由此你能做出什么猜测?
03
新知讲解
AB=DC,AD=BC, ∠A=∠C, ∠B=∠D
你能证明吗?
03
新知讲解
∵ 四边形 ABCD 为平行四边形,
∴ AB ∥ DC, AD ∥ BC (平行四边形的两组对 边分别平行).
∴ ∠1= ∠2, ∠3= ∠4.
又 AC=CA,
∴ △ABC≌△CDA.
∴ AB = CD, BC = DA, ∠B = ∠D. 又 ∠1+ ∠4= ∠2+ ∠3,
∴ ∠BAD = ∠DCB.
如图, 连接 AC.
证明:
03
新知讲解
平行四边形的性质定理:
总结
平行四边形的对边相等, 平行四边形的对角相等.
∵四边形ABCD是平行四边形
几何语言
∴AB=CD,BC=AD.
∴∠A=∠C,∠B=∠D.
A
B
C
D
新课探究
例1
如图, 四边形ABCD和BCEF均为平行四边形,AD=2cm, ∠A=65°,∠E=33°,求EF和∠BGC.
03
新知讲解
解 ∵ 四边形ABCD是平行四边形,
∴ AD=BC=2cm,∠1=∠A=65°.
∵ 四边形BCEF是平行四边形,
∴ EF=BC=2cm,∠2=∠E=33°.
∴ 在△BGC中,∠BGC=180°-∠1-∠2=82°.
03
新知讲解
例2、如图,直线 l1与l2平行,AB,CD是l1与l2之间的任意两条平行线段. 试问:AB与CD是否相等?为什么?
解 ∵ l1∥l2,AB∥CD,
∴ 四边形ABDC是平行四边形.
∴ AB=CD.
结论:
夹在两条平行线间的平行线段相等
03
新知讲解
若a//b,DA、GH、CB垂直于a,交a于A、G、B,交b于D、H、C.
则DA=GH=CB
两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离.
两条平行线之间的距离相等
04
课堂练习
【知识技能类作业】必做题:
1.如图,在□ABCD中,AD=3 cm,AB=2 cm,则□ABCD的周长等于( )
A.10 cm B.6 cm C.5 cm D.4 cm
A
04
课堂练习
【知识技能类作业】选做题:
2.如图,过□ABCD的对角线BD上一点M分别作平行四边形两边的平行线EF与GH,那么图中的□AEMG的面积S1与□HCFM的面积S2的大小关系是( )
A.S1>S2 B.S1
04
课堂练习
【综合拓展类作业】
3.已知:平行四边形□ABCD的周长为60cm,两邻边AB,BC长的比为3:2,求AB和BC的长度 .
解:∵四边形ABCD是平行四边形(已知)
∴ AB=CD,BC=AD(平行四边形的对边相等)
又∵□ABCD的周长为60cm.
∴AB+BC=30cm.
又AB:BC=3:2,即AB=1.5BC.
则1.5BC+BC=30 , 解得BC=12 (cm).
而AB=1.5×12=18 (cm).
05
课堂小结
平行四边形的性质
3、平行线间的平行线段
有两组对边分别平行的四边形叫做平行四边形。
1、平行四边形的定义
平行四边形的对边相等, 平行四边形的对角相等.
夹在两条平行线间的平行线段相等
2、平行四边形的性质
06
作业布置
【知识技能类作业】必做题:
1、如图,在□ABCD中,BE⊥AD于点E,若∠ABE=50°,则∠C=__________.
40°
06
作业布置
【知识技能类作业】选做题:
2、如图,□ABCD与□DCFE的周长相等,且∠BAD=60°,∠F=110°,则∠DAE的度数为__________.
25°
06
作业布置
【综合拓展类作业】
3、已知:在□ABCD中,AE⊥BC,垂足为点E,CE=CD,点F为CE的中点,点G为CD上的一点,连接DF、EG、AG,若CF=2,AE=3,求BE的长;
06
作业布置
【综合拓展类作业】
解:∵点F为CE的中点,
∴CE=CD=2CF=4.
又∵四边形ABCD为平行四边形,
∴AB=CD=4.
在Rt△ABE中,由勾股定理得BE== .
Thanks!
https://www.21cnjy.com/recruitment/home/fine
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
