人教版九年级数学第一学期期末模拟测试题(含解析)
文档属性
| 名称 | 人教版九年级数学第一学期期末模拟测试题(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-13 08:09:31 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版九年级数学第一学期期末模拟测试题
考试范围:人教版九年级第21章-第26章;考试时间:100分钟;总分:120分
一.选择题(共10小题,满分30分,每小题3分)
1.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.已知关于x的一元二次方程x2﹣(2m﹣1)x+m2=0有实数根,则m的取值范围是( )
A.m≠0 B.m C.m D.m
3.一个不透明的袋子中有1个红球、2个黄球,这些球除颜色外无其他差别,从袋子中随机摸出1个球后放回,再随机摸出1个球,两次摸出的球都是黄球的概率( )
A. B. C. D.
4.如图,⊙O的半径为6,AB为弦,点C为的中点,若∠ABC=30°,则弦AB的长为( )
A. B.6 C. D.
(4题图) (5题图) (7题图) (8题图)
5.如图,将△ABC绕点A逆时针旋转角α(0°<α<180°)得到△ADE,点B的对应点D恰好落在BC边上,若DE⊥AC,∠CAD=25°,则旋转角α的度数是( )
A.40° B.50° C.60° D.70°
6.在函数y(k<0)的图象上有A(1,y1)、B(﹣1,y2)、C(﹣2,y3)三个点,则下列各式中正确的是( )
A.y1<y2<y3 B.y3<y2<y1 C.y1<y3<y2 D.y2<y3<y1
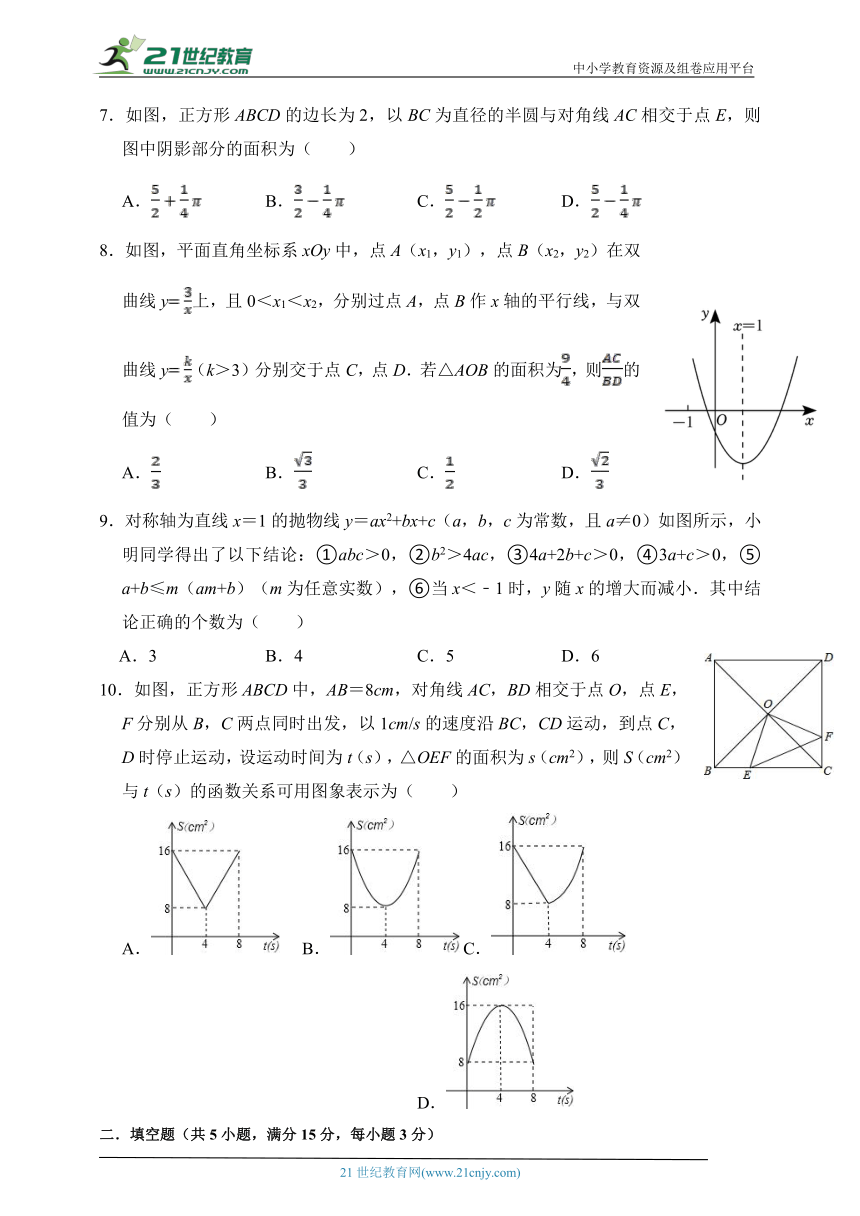
7.如图,正方形ABCD的边长为2,以BC为直径的半圆与对角线AC相交于点E,则图中阴影部分的面积为( )
A. B. C. D.
8.如图,平面直角坐标系xOy中,点A(x1,y1),点B(x2,y2)在双曲线y上,且0<x1<x2,分别过点A,点B作x轴的平行线,与双曲线y(k>3)分别交于点C,点D.若△AOB的面积为,则的值为( )
A. B. C. D.
9.对称轴为直线x=1的抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)如图所示,小明同学得出了以下结论:①abc>0,②b2>4ac,③4a+2b+c>0,④3a+c>0,⑤a+b≤m(am+b)(m为任意实数),⑥当x<﹣1时,y随x的增大而减小.其中结论正确的个数为( )
A.3 B.4 C.5 D.6
10.如图,正方形ABCD中,AB=8cm,对角线AC,BD相交于点O,点E,F分别从B,C两点同时出发,以1cm/s的速度沿BC,CD运动,到点C,D时停止运动,设运动时间为t(s),△OEF的面积为s(cm2),则S(cm2)与t(s)的函数关系可用图象表示为( )
A. B. C. D.
二.填空题(共5小题,满分15分,每小题3分)
11.若点P(m+1,8﹣2m)关于原点的对称点Q在第三象限,那么m的取值范围是 .
12.如图,AB是⊙O的直径,CD是⊙O的切线,C为切点,AB的延长线交直线CD于点E,连接AC,BC.若∠ACD=60°,AC=3,则BE的长度是 .
(12题图) (13题图) (14题图) (15题图)
13.如图,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,点P、Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最大值与最小值的和是 .
14.如图,点P(﹣2,3),过P作PC∥x轴,PB∥y轴,并分别交双曲线于C、B两点,连接OB、OC,若S四边形OBPC=4,则k= .
15.如图,在正方形ABCD中,,点E在BC边上(不与端点重合),将△CDE沿DE折叠,使点C落在点F处,连接AF,BF,当△ABF是等腰三角形时,CE的长等于 .
三.解答题(共8小题,满分75分)
16.(8分)解方程:
(1)x2+4x﹣12=0 (2)3(x﹣5)2=2(x﹣5)
17.(9分)已知m,n是关于x的一元二次方程x2﹣2(a+1)x+a2+5=0的两实数根.
(1)若(m﹣1)(n﹣1)=28,求a的值;
(2)已知等腰△ABC的一边长为7,若m,n恰好是△ABC另外两边的边长,求△ABC的周长.
18.(9分)阅读对一个人的成长的影响是巨大的,一本好书往往能改变人的一生.某中学为了解学生阅读课外书籍的情况,决定围绕“在艺术、科技、动漫、小说、其他五类课外书籍中,你最喜欢哪一类”的问题,在全校范围内随机抽取部分同学进行问卷调查,并将调查结果绘制成如下两幅不完整的统计图.
请根据图中信息解答下列问题:
(1)本次调查随机抽取的学生有 人;
(2)请补全条形统计图;
(3)若该校共有1600名学生,请你估计这1600人中最喜欢“动漫”类书籍的有多少人?
(4)小东从图书馆借回2本动漫书和2本科技书放进一个空书包里准备回家阅读,他从书包里任取2本,用画树状图或列表的方法求恰好都是“科技”类图书的概率.
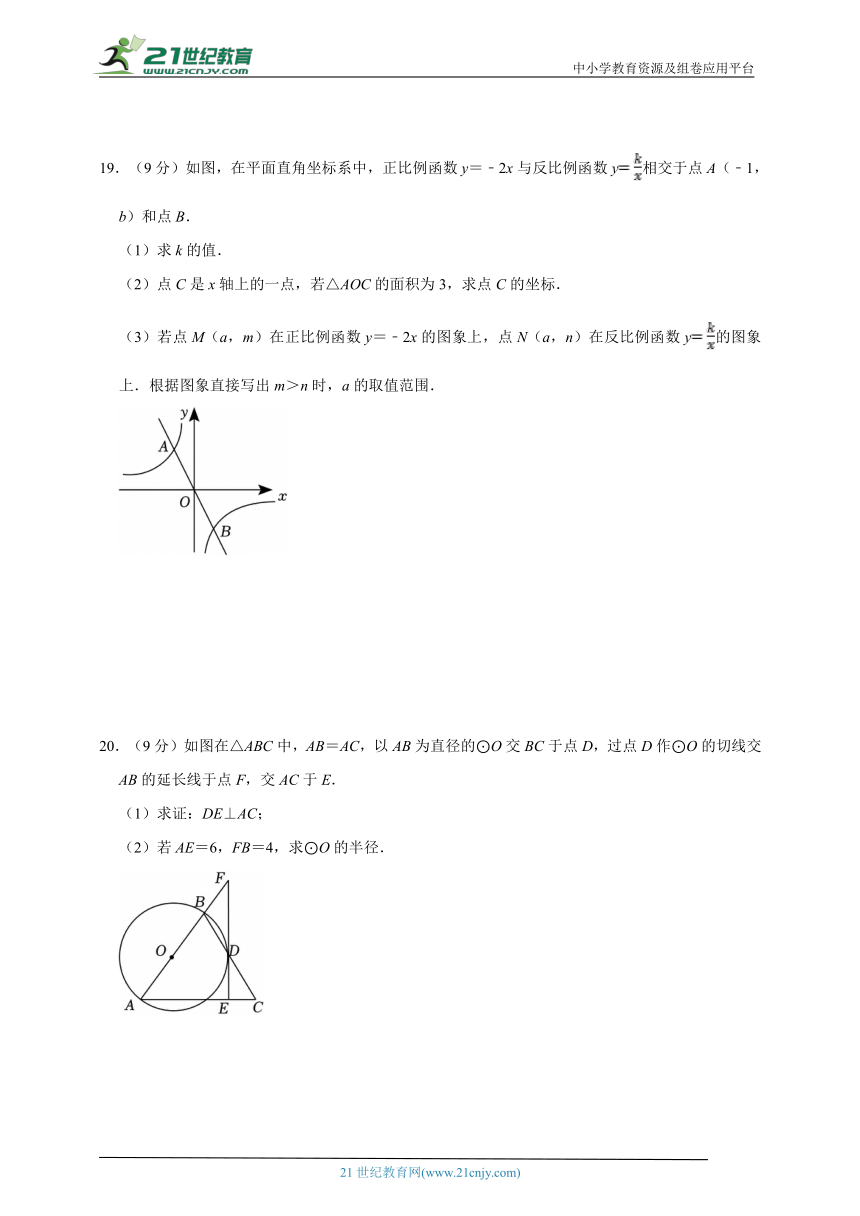
19.(9分)如图,在平面直角坐标系中,正比例函数y=﹣2x与反比例函数y相交于点A(﹣1,b)和点B.
(1)求k的值.
(2)点C是x轴上的一点,若△AOC的面积为3,求点C的坐标.
(3)若点M(a,m)在正比例函数y=﹣2x的图象上,点N(a,n)在反比例函数y的图象上.根据图象直接写出m>n时,a的取值范围.
20.(9分)如图在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作⊙O的切线交AB的延长线于点F,交AC于E.
(1)求证:DE⊥AC;
(2)若AE=6,FB=4,求⊙O的半径.
21.(10分)在某场篮球比赛中,一位运动员在距篮下7m,三分线外跳起投篮,球运行的路线大致是抛物线,当球运行的水平距离为4m时,球达到最大高度,然后准确落入篮圈,篮圈中心到地面的距离为3.05m,当建立如图所示的平面直角坐标系时,可知抛物线的表达式为y=﹣0.09x2+3.86.
(1)请直接写出球达到的最大高度是多少?
(2)该运动员身高1.84m,在这次跳投中,球在头顶上方0.3m处出手,问:球出手时,她跳离地面的高度是多少?
22.(10分)某经销商以每箱12元的价格购进一批消毒水进行销售,当每箱售价为26元时,日均销量为60箱.为了增加销量,该经销商准备适当降价.经市场调查发现,每箱消毒水降价1元,则可以多销售5箱.设每箱降价x元,日均销量为y箱.
(1)求日均销量y关于x的函数关系式.
(2)要使日均利润为800元,则每箱应降价多少元?
(3)促销后发现,该经销商每天的销售量不低于85箱.若每销售一箱消毒水可以享受政府m元(0<m≤6)的补贴,且销售这种消毒水的日均最大利润为1020元,求m的值.
23.(11分)如图1,将一副三角板的直角重合放置,其中∠A=30°,∠CDE=45°.
(1)如图1,求∠EFB的度数;
(2)若三角板ACB的位置保持不动,将三角板CDE绕其直角顶点C顺时针方向旋转.
①当旋转至如图2所示位置时,恰好CD∥AB,则∠ECB的度数为 °;
②若将三角板CDE继续绕点C旋转,直至回到图1位置.在这一过程中,是否还会存在△CDE其中一边与AB平行?如果存在,请你画出示意图,并直接写出相应的∠ECB的大小;如果不存在,请说明理由.
参考答案
1.解:A、不是轴对称图形,是中心对称图形,此选项不合题意;
B、是轴对称图形,不是中心对称图形,此选项不合题意;
C、是轴对称图形,是中心对称图形,此选项符合题意;
D、是轴对称图形,不是中心对称图形,此选项不合题意;
选:C.
2.解:根据题意得,Δ=b2﹣4ac=[﹣(2m﹣1)]2﹣4m2=﹣4m+1≥0,
解得:m,
选:B.
3.解:画树状图为:
共有9种等可能的结果数,其中两次摸出的球都是黄球的结果数为4,
所以两次摸出的球都是黄球的概率为.
选:D.
4.解:如图,连接OB,OA,OC,OC交AB于E.
∵∠AOC=2∠ABC=2×30°=60°,
∵点C为的中点,
∴OC⊥AB,
∴AE=EB,
在Rt△AOE中,AE==3,
∴AB=2AE=6,
选:D.
5.解:根据题意,
∵DE⊥AC,∠CAD=25°,
∴∠ADE=90°﹣25°=65°,
由旋转的性质可得∠B=∠ADE,AB=AD,
∴∠ADB=∠B=65°,
∴∠BAD=180°﹣65°﹣65°=50°,
∴旋转角α的度数是50°;
选:B.
6.解:∵y(k<0)的图象上有A(1,y1)、B(﹣1,y2)、C(﹣2,y3)三个点,
∴1×y1=k,﹣1×y2=k,﹣2×y3=k,
∴y1=k,y2=﹣k,y3k,
而k<0,
∴y1<y3<y2.
选:C.
7.解:连接OE.
∵S△ADCAD CD2×2=2,
S扇形OCEπ×12,
S△COE1×1,
∴S弓形CE,
∴阴影部分的面积为2﹣().
选:D.
8.解:如图,过点A作AF⊥x轴于点F,过点B作BH⊥x轴于点H,
∵A(x1,y1),点B(x2,y2)在双曲线y上,
∴AF,BH,FH=x2﹣x1,S△AOF,S△BOH,
∴S梯形ABHFFH (AF+BH),
∵S△AOB=S△AOF+S梯形ABHF﹣S△BOH,
∴x22﹣x12x1x2,即,
令t,则t,t>1,
解得:t=2或t(舍),
∴2,
∵AC∥BD∥x轴,点C,点D在双曲线y(k>3)图象上,
∴点C(,),点D(,),
∴ACx1,BDx2,
∴,
选:C.
9.解:①由图象可知:a>0,c<0,
∵对称轴为直线:,
∴b=﹣2a<0,
∴abc>0,①正确;
②∵抛物线与x轴有两个交点,
∴b2﹣4ac>0,
∴b2>4ac,②正确;
③∵对称轴为直线x=1,则x=0与x=2的函数值相等,
∴当x=2时,y=4a+2b+c<0,③错误;
④当x=﹣1时,y=a﹣b+c=a﹣(﹣2a)+c>0,
∴3a+c>0,④正确;
⑤当x=1时,y取到最小值,此时,y=a+b+c,
而当x=m时,y=am2+bm+c,
所以a+b+c≤am2+bm+c,
a+b≤am2+bm,即a+b≤m(am+b),⑤正确,
⑥当x<﹣1时,y随x的增大而减小,⑥正确,
综上,正确的是①②④⑤⑥共5个,
选:C.
10.解:根据题意BE=CF=t,CE=8﹣t,
∵四边形ABCD为正方形,
∴OB=OC,∠OBC=∠OCD=45°,
∵在△OBE和△OCF中
,
∴△OBE≌△OCF(SAS),
∴S△OBE=S△OCF,
∴S四边形OECF=S△OBC82=16,
∴S=S四边形OECF﹣S△CEF=16(8﹣t) tt2﹣4t+16(t﹣4)2+8(0≤t≤8),
∴s(cm2)与t(s)的函数图象为抛物线一部分,顶点为(4,8),自变量为0≤t≤8.
选:B.
二.填空题(共10小题)
11.解:点P(m+1,8﹣2m)关于原点的对称点Q的坐标为(﹣m﹣1,﹣8+2m),
由题意得,,
解得,﹣1<m<4,
答案为:﹣1<m<4.
12.解:连接OC,
则OC=OA=OB,
∵CD与⊙O相切于点C,∠ACD=60°,
∴CD⊥OC,
∴∠OCD=∠OCE=90°,
∴∠A=∠OCA=90°﹣∠ACD=30°,
∴∠BOC=2∠A=60°,
∴∠E=90°﹣∠BOC=30°=∠A,△BOC是等边三角形,
∴EC=AC=3,BC=OB,∠OBC=60°,
∴∠BCE=∠OBC﹣∠E=60°﹣30°=30°=∠E,
∴BE=BC=OB=OC,
∴OE=2BE,
∴,
∴,
答案为:.
13.解:如图,设⊙O与AC相切于点E,连接OE,作OP1⊥BC垂足为P1交⊙O于Q1,
此时垂线段OP1最短,P1Q1最小值为OP1﹣OQ1,
∵AB=10,AC=8,BC=6,
∴AB2=AC2+BC2,
∴∠C=90°,
∵∠OP1B=90°,
∴OP1∥AC
∵AO=OB,
∴P1C=P1B,
∴OP1AC=4,
∴P1Q1最小值为OP1﹣OQ1=1,
如图,当Q2在AB边上时,P2与B重合时,P2Q2经过圆心,经过圆心的弦最长,
P2Q2最大值=5+3=8,
∴PQ长的最大值与最小值的和是9.
答案为:9.
14.解:∵点P(﹣2,3),过P作PC∥x轴,PB∥y轴,
∴当x=﹣2时,y,当y=3时,x,
∴点B、C的坐标为B(﹣2,),C(,3),
延长PB交x轴于点E,延长PC交y轴于点F,
则S四边形OBPC=S矩形PEOF﹣S△OBE﹣S△OCF,
=|﹣2|×3|﹣2| ||||×3,
=6﹣|k|,
根据图象可得k<0,
又∵S四边形OBPC=4,
∴6+k=4,
解得k=﹣2.
答案为:﹣2.
15.解:当△ABF是等腰三角形时,有三种情况:
①AB=AF,如图,
过点F作GH⊥BC交AD于G,交BC于H,
∵四边形ABCD是正方形,AD,
∴四边形ABHG和四边形CDGH都是矩形,
∴GH=AB=DC=AD,
∵将△CDE沿DE折叠,使点C落在点F处,
∴DF=DC=AF=AD,FE=CE,
∴HC=GDAD,FGGD,
∴FH=GH﹣FG,EH=HC﹣ECEC,
在Rt△EFH中,
由勾股定理,得FH2+EH2=EF2,
即()2+(CE)2=CE2,
解得CE;
②FA=FB,如图,
过点F作GH⊥BC交AD于G,交BC于H,
则∠FAB=∠FBA,
∵四边形ABCD是正方形,AD,
∴四边形ABHG和四边形CDGH都是矩形,
∴GH=AB=DC=AD,∠BAD=∠ABC=∠AGF=∠BHF=90°,AG=BH,
∴∠FAG=∠FBH,
∴△FAG≌△FBH(AAS),
∴FG=FH,
∵将△CDE沿DE折叠,使点C落在点F处,
∴DF=DC=AD,EF=EC,
在Rt△DFH中,
由勾股定理,得DG,
∴CH,HE=CH﹣CECE,
在Rt△EFH中,
由勾股定理,得FH2+EH2=EF2,
即()2+(CE)2=CE2,
解得CE=1;
③BF=BA,此时点E与点B重合,不合题意,
综上,CE或1.
答案为:或1.
三.解答题(共8小题,满分75分)
16.解:(1)∵(x﹣2)(x+6)=0,
∴x﹣2=0或x+6=0,
解得:x=2或x=﹣6;
(2)∵3(x﹣5)2﹣2(x﹣5)=0,
∴(x﹣5)(3x﹣17)=0,
则x﹣5=0或3x﹣17=0,
解得:x=5或x.
17.解:(1)由根与系数关系得:m+n=2(a+1),mn=a2+5
依题意得:(m﹣1)(n﹣1)=28,
mn﹣m﹣n+1=28,
a2+5﹣2(a+1)+1=28,
a2﹣2a﹣24=0,
解得:a1=6,a2=﹣4,
由△≥0得:[﹣2(a+1)]2﹣4(a2+5)≥0,
a≥2,
∴a=6;
(2)分两种情况:
①当m=7或n=7时,即方程有一根为7,把x=7代入方程得:49﹣14(a+1)+a2+5=0,
整理得a2﹣14a+40=0,解得a1=10,a2=4,
当a=10时,x1+x2=2(a+1)=22,解得x2=15,而7+7<15,舍去;
当a=4时,x1+x2=2(a+1)=10,解得x2=3,则三角形周长为3+7+7=17;
②当m=n时,即方程有两个相等实根,x1=x2,则Δ=0,a=2,方程化为x2﹣6x+9=0,解得x1=x2=3,则3+3<7,舍去,
所以这个三角形的周长为17.
18.解:(1)∵抽样人数为2÷4%=50(人).
答案为:50;
(2)∵抽样人数为50人,
∴小说类的人数为50×40%=20(人),
补全条形统计图如下:
(3)∵抽样人数为50人,
∴动漫的百分比为12÷50=24%,
∴喜欢动漫类书籍的人数约为1600×24%=384(人),
答:估计这1600人中最喜欢动漫类书籍的有384人;
(4)画树状图如下:
由图知,共有12种等可能结果,其中都是“科技类”图书的有2种结果,
∴都是科技类图书的概率为.
19.解:(1)∵正比例函数y=﹣2x经过点A(﹣1,b),
∴b=﹣2×(﹣1)=2,
∴A(﹣1,2),
∵点A在反比例函数y图象上,
∴k=﹣1×2=﹣2;
(2)∵点C是x轴上的一点,△AOC的面积为3,
∴OC yA=3,即OC 2=3,
∴OC=3,
∴点C的坐标为(﹣3,0)或(3,0);
(3)∵正比例函数y=﹣2x与反比例函数y相交于点A(﹣1,2)和点B,
∴B(1,﹣2),
∵点M(a,m)在正比例函数y=﹣2x的图象上,点N(a,n)在反比例函数y的图象上,
∴MN∥y轴,
由图象可知,当m>n时,a的取值范围a<﹣1或0<a<1.
20.解析:(1)连结AD、OD,如图,
∵AB为⊙O的直径,
∴∠ADB=90°,即AD⊥BC,
∵AB=AC,
∴BD=CD,
而OA=OB,
∴OD为△ABC 的中位线,
∴OD∥AC,
∵EF是⊙O的切线;
∴OD⊥EF
OD∥AC,
∴EF⊥AC;
(2)设⊙O的半径为R,
∵OD∥AE,
∴△FOD∽△FAE,
∴,
∴,
∴R=4或(﹣3舍弃).
∴⊙O的半径为4.
21.解:(1)依题意,当球运行的水平距离为4m时,球达到最大高度,即x=0时,取得最大值,
将x=0,代入y=﹣0.09x2+3.86,
解得:y=3.86.
∴球达到的最大高度是3.86 m.
(2)设运动员跳离地面高度为hm,
将x=﹣4代入二次函数y=﹣0.09x2+3.86,
得h+1.84+0.3=﹣0.09×16+3.86,
解得h=0.28.
答:运动员跳离地面的高度是0.28 m.
22.解:(1)∵每箱消毒水降价1元,则可以多销售5箱,每箱降价x元,
∴日均销量多销售5x箱,
∴日均销量y关于x的函数关系式为y=5x+60.
(2)由题意得:
(26﹣x﹣12)(5x+60)=800,
整理得:x2﹣2x﹣8=0,
解得x1=4,x2=﹣2(不合题意,舍去);
∴要使日均利润为800元,则每箱应降价4元.
(3)由题意得5x+60≥85,
∴x≥5,
设销售这种消毒水的日均利润为w元,由题意得:
w=(26﹣x﹣12)(5x+60)+m(5x+60)
=(5x+60)(14﹣x+m)
=﹣5x2+10x+840+5mx+60m
=﹣5x2+(10+5m)x+840+60m,
∵﹣5<0,抛物线开口向下,
∴当x1时,w有最大值,
∵0<m≤6,
∴对称轴取值范围小于等于4,
∴当x=5时,w取最大值,即(5×5+60)(14﹣5+m)=1020,
解得m=3.
23.解:(1)∵∠A=30°,∠CDE=45°,
∴∠ABC=90°﹣30°=60°,∠E=90°﹣45°=45°,
∴∠EFB=∠ABC﹣∠E=60°﹣45°=15°;
(2)①∵CD∥AB,
∴∠ACD=∠A=30°,
∵∠ACD+∠ACE=∠DCE=90°,
∠ECB+∠ACE=∠ACB=90°,
∴∠ECB=∠ACD=30°;
②如图1,CE∥AB,∠ACE=∠A=30°,
∠ECB=∠ACB+∠ACE=90°+30°=120°;
如图2,DE∥AB时,延长CD交AB于F,
则∠BFC=∠D=45°,
在△BCF中,∠BCF=180°﹣∠B﹣∠BFC,
=180°﹣60°﹣45°=75°,
∴∠ECB=∠BCF+∠ECF=75°+90°=165°;
如图3,CD∥AB时,∠BCD=∠B=60°,
∠ECB=∠BCD+∠EDC=60°+90°=150°;
如图4,CE∥AB时,∠ECB=∠B=60°,
如图5,DE∥AB或DE与AB在同一条直线上时,∠ECB=60°﹣45°=15°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版九年级数学第一学期期末模拟测试题
考试范围:人教版九年级第21章-第26章;考试时间:100分钟;总分:120分
一.选择题(共10小题,满分30分,每小题3分)
1.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.已知关于x的一元二次方程x2﹣(2m﹣1)x+m2=0有实数根,则m的取值范围是( )
A.m≠0 B.m C.m D.m
3.一个不透明的袋子中有1个红球、2个黄球,这些球除颜色外无其他差别,从袋子中随机摸出1个球后放回,再随机摸出1个球,两次摸出的球都是黄球的概率( )
A. B. C. D.
4.如图,⊙O的半径为6,AB为弦,点C为的中点,若∠ABC=30°,则弦AB的长为( )
A. B.6 C. D.
(4题图) (5题图) (7题图) (8题图)
5.如图,将△ABC绕点A逆时针旋转角α(0°<α<180°)得到△ADE,点B的对应点D恰好落在BC边上,若DE⊥AC,∠CAD=25°,则旋转角α的度数是( )
A.40° B.50° C.60° D.70°
6.在函数y(k<0)的图象上有A(1,y1)、B(﹣1,y2)、C(﹣2,y3)三个点,则下列各式中正确的是( )
A.y1<y2<y3 B.y3<y2<y1 C.y1<y3<y2 D.y2<y3<y1
7.如图,正方形ABCD的边长为2,以BC为直径的半圆与对角线AC相交于点E,则图中阴影部分的面积为( )
A. B. C. D.
8.如图,平面直角坐标系xOy中,点A(x1,y1),点B(x2,y2)在双曲线y上,且0<x1<x2,分别过点A,点B作x轴的平行线,与双曲线y(k>3)分别交于点C,点D.若△AOB的面积为,则的值为( )
A. B. C. D.
9.对称轴为直线x=1的抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)如图所示,小明同学得出了以下结论:①abc>0,②b2>4ac,③4a+2b+c>0,④3a+c>0,⑤a+b≤m(am+b)(m为任意实数),⑥当x<﹣1时,y随x的增大而减小.其中结论正确的个数为( )
A.3 B.4 C.5 D.6
10.如图,正方形ABCD中,AB=8cm,对角线AC,BD相交于点O,点E,F分别从B,C两点同时出发,以1cm/s的速度沿BC,CD运动,到点C,D时停止运动,设运动时间为t(s),△OEF的面积为s(cm2),则S(cm2)与t(s)的函数关系可用图象表示为( )
A. B. C. D.
二.填空题(共5小题,满分15分,每小题3分)
11.若点P(m+1,8﹣2m)关于原点的对称点Q在第三象限,那么m的取值范围是 .
12.如图,AB是⊙O的直径,CD是⊙O的切线,C为切点,AB的延长线交直线CD于点E,连接AC,BC.若∠ACD=60°,AC=3,则BE的长度是 .
(12题图) (13题图) (14题图) (15题图)
13.如图,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,点P、Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最大值与最小值的和是 .
14.如图,点P(﹣2,3),过P作PC∥x轴,PB∥y轴,并分别交双曲线于C、B两点,连接OB、OC,若S四边形OBPC=4,则k= .
15.如图,在正方形ABCD中,,点E在BC边上(不与端点重合),将△CDE沿DE折叠,使点C落在点F处,连接AF,BF,当△ABF是等腰三角形时,CE的长等于 .
三.解答题(共8小题,满分75分)
16.(8分)解方程:
(1)x2+4x﹣12=0 (2)3(x﹣5)2=2(x﹣5)
17.(9分)已知m,n是关于x的一元二次方程x2﹣2(a+1)x+a2+5=0的两实数根.
(1)若(m﹣1)(n﹣1)=28,求a的值;
(2)已知等腰△ABC的一边长为7,若m,n恰好是△ABC另外两边的边长,求△ABC的周长.
18.(9分)阅读对一个人的成长的影响是巨大的,一本好书往往能改变人的一生.某中学为了解学生阅读课外书籍的情况,决定围绕“在艺术、科技、动漫、小说、其他五类课外书籍中,你最喜欢哪一类”的问题,在全校范围内随机抽取部分同学进行问卷调查,并将调查结果绘制成如下两幅不完整的统计图.
请根据图中信息解答下列问题:
(1)本次调查随机抽取的学生有 人;
(2)请补全条形统计图;
(3)若该校共有1600名学生,请你估计这1600人中最喜欢“动漫”类书籍的有多少人?
(4)小东从图书馆借回2本动漫书和2本科技书放进一个空书包里准备回家阅读,他从书包里任取2本,用画树状图或列表的方法求恰好都是“科技”类图书的概率.
19.(9分)如图,在平面直角坐标系中,正比例函数y=﹣2x与反比例函数y相交于点A(﹣1,b)和点B.
(1)求k的值.
(2)点C是x轴上的一点,若△AOC的面积为3,求点C的坐标.
(3)若点M(a,m)在正比例函数y=﹣2x的图象上,点N(a,n)在反比例函数y的图象上.根据图象直接写出m>n时,a的取值范围.
20.(9分)如图在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作⊙O的切线交AB的延长线于点F,交AC于E.
(1)求证:DE⊥AC;
(2)若AE=6,FB=4,求⊙O的半径.
21.(10分)在某场篮球比赛中,一位运动员在距篮下7m,三分线外跳起投篮,球运行的路线大致是抛物线,当球运行的水平距离为4m时,球达到最大高度,然后准确落入篮圈,篮圈中心到地面的距离为3.05m,当建立如图所示的平面直角坐标系时,可知抛物线的表达式为y=﹣0.09x2+3.86.
(1)请直接写出球达到的最大高度是多少?
(2)该运动员身高1.84m,在这次跳投中,球在头顶上方0.3m处出手,问:球出手时,她跳离地面的高度是多少?
22.(10分)某经销商以每箱12元的价格购进一批消毒水进行销售,当每箱售价为26元时,日均销量为60箱.为了增加销量,该经销商准备适当降价.经市场调查发现,每箱消毒水降价1元,则可以多销售5箱.设每箱降价x元,日均销量为y箱.
(1)求日均销量y关于x的函数关系式.
(2)要使日均利润为800元,则每箱应降价多少元?
(3)促销后发现,该经销商每天的销售量不低于85箱.若每销售一箱消毒水可以享受政府m元(0<m≤6)的补贴,且销售这种消毒水的日均最大利润为1020元,求m的值.
23.(11分)如图1,将一副三角板的直角重合放置,其中∠A=30°,∠CDE=45°.
(1)如图1,求∠EFB的度数;
(2)若三角板ACB的位置保持不动,将三角板CDE绕其直角顶点C顺时针方向旋转.
①当旋转至如图2所示位置时,恰好CD∥AB,则∠ECB的度数为 °;
②若将三角板CDE继续绕点C旋转,直至回到图1位置.在这一过程中,是否还会存在△CDE其中一边与AB平行?如果存在,请你画出示意图,并直接写出相应的∠ECB的大小;如果不存在,请说明理由.
参考答案
1.解:A、不是轴对称图形,是中心对称图形,此选项不合题意;
B、是轴对称图形,不是中心对称图形,此选项不合题意;
C、是轴对称图形,是中心对称图形,此选项符合题意;
D、是轴对称图形,不是中心对称图形,此选项不合题意;
选:C.
2.解:根据题意得,Δ=b2﹣4ac=[﹣(2m﹣1)]2﹣4m2=﹣4m+1≥0,
解得:m,
选:B.
3.解:画树状图为:
共有9种等可能的结果数,其中两次摸出的球都是黄球的结果数为4,
所以两次摸出的球都是黄球的概率为.
选:D.
4.解:如图,连接OB,OA,OC,OC交AB于E.
∵∠AOC=2∠ABC=2×30°=60°,
∵点C为的中点,
∴OC⊥AB,
∴AE=EB,
在Rt△AOE中,AE==3,
∴AB=2AE=6,
选:D.
5.解:根据题意,
∵DE⊥AC,∠CAD=25°,
∴∠ADE=90°﹣25°=65°,
由旋转的性质可得∠B=∠ADE,AB=AD,
∴∠ADB=∠B=65°,
∴∠BAD=180°﹣65°﹣65°=50°,
∴旋转角α的度数是50°;
选:B.
6.解:∵y(k<0)的图象上有A(1,y1)、B(﹣1,y2)、C(﹣2,y3)三个点,
∴1×y1=k,﹣1×y2=k,﹣2×y3=k,
∴y1=k,y2=﹣k,y3k,
而k<0,
∴y1<y3<y2.
选:C.
7.解:连接OE.
∵S△ADCAD CD2×2=2,
S扇形OCEπ×12,
S△COE1×1,
∴S弓形CE,
∴阴影部分的面积为2﹣().
选:D.
8.解:如图,过点A作AF⊥x轴于点F,过点B作BH⊥x轴于点H,
∵A(x1,y1),点B(x2,y2)在双曲线y上,
∴AF,BH,FH=x2﹣x1,S△AOF,S△BOH,
∴S梯形ABHFFH (AF+BH),
∵S△AOB=S△AOF+S梯形ABHF﹣S△BOH,
∴x22﹣x12x1x2,即,
令t,则t,t>1,
解得:t=2或t(舍),
∴2,
∵AC∥BD∥x轴,点C,点D在双曲线y(k>3)图象上,
∴点C(,),点D(,),
∴ACx1,BDx2,
∴,
选:C.
9.解:①由图象可知:a>0,c<0,
∵对称轴为直线:,
∴b=﹣2a<0,
∴abc>0,①正确;
②∵抛物线与x轴有两个交点,
∴b2﹣4ac>0,
∴b2>4ac,②正确;
③∵对称轴为直线x=1,则x=0与x=2的函数值相等,
∴当x=2时,y=4a+2b+c<0,③错误;
④当x=﹣1时,y=a﹣b+c=a﹣(﹣2a)+c>0,
∴3a+c>0,④正确;
⑤当x=1时,y取到最小值,此时,y=a+b+c,
而当x=m时,y=am2+bm+c,
所以a+b+c≤am2+bm+c,
a+b≤am2+bm,即a+b≤m(am+b),⑤正确,
⑥当x<﹣1时,y随x的增大而减小,⑥正确,
综上,正确的是①②④⑤⑥共5个,
选:C.
10.解:根据题意BE=CF=t,CE=8﹣t,
∵四边形ABCD为正方形,
∴OB=OC,∠OBC=∠OCD=45°,
∵在△OBE和△OCF中
,
∴△OBE≌△OCF(SAS),
∴S△OBE=S△OCF,
∴S四边形OECF=S△OBC82=16,
∴S=S四边形OECF﹣S△CEF=16(8﹣t) tt2﹣4t+16(t﹣4)2+8(0≤t≤8),
∴s(cm2)与t(s)的函数图象为抛物线一部分,顶点为(4,8),自变量为0≤t≤8.
选:B.
二.填空题(共10小题)
11.解:点P(m+1,8﹣2m)关于原点的对称点Q的坐标为(﹣m﹣1,﹣8+2m),
由题意得,,
解得,﹣1<m<4,
答案为:﹣1<m<4.
12.解:连接OC,
则OC=OA=OB,
∵CD与⊙O相切于点C,∠ACD=60°,
∴CD⊥OC,
∴∠OCD=∠OCE=90°,
∴∠A=∠OCA=90°﹣∠ACD=30°,
∴∠BOC=2∠A=60°,
∴∠E=90°﹣∠BOC=30°=∠A,△BOC是等边三角形,
∴EC=AC=3,BC=OB,∠OBC=60°,
∴∠BCE=∠OBC﹣∠E=60°﹣30°=30°=∠E,
∴BE=BC=OB=OC,
∴OE=2BE,
∴,
∴,
答案为:.
13.解:如图,设⊙O与AC相切于点E,连接OE,作OP1⊥BC垂足为P1交⊙O于Q1,
此时垂线段OP1最短,P1Q1最小值为OP1﹣OQ1,
∵AB=10,AC=8,BC=6,
∴AB2=AC2+BC2,
∴∠C=90°,
∵∠OP1B=90°,
∴OP1∥AC
∵AO=OB,
∴P1C=P1B,
∴OP1AC=4,
∴P1Q1最小值为OP1﹣OQ1=1,
如图,当Q2在AB边上时,P2与B重合时,P2Q2经过圆心,经过圆心的弦最长,
P2Q2最大值=5+3=8,
∴PQ长的最大值与最小值的和是9.
答案为:9.
14.解:∵点P(﹣2,3),过P作PC∥x轴,PB∥y轴,
∴当x=﹣2时,y,当y=3时,x,
∴点B、C的坐标为B(﹣2,),C(,3),
延长PB交x轴于点E,延长PC交y轴于点F,
则S四边形OBPC=S矩形PEOF﹣S△OBE﹣S△OCF,
=|﹣2|×3|﹣2| ||||×3,
=6﹣|k|,
根据图象可得k<0,
又∵S四边形OBPC=4,
∴6+k=4,
解得k=﹣2.
答案为:﹣2.
15.解:当△ABF是等腰三角形时,有三种情况:
①AB=AF,如图,
过点F作GH⊥BC交AD于G,交BC于H,
∵四边形ABCD是正方形,AD,
∴四边形ABHG和四边形CDGH都是矩形,
∴GH=AB=DC=AD,
∵将△CDE沿DE折叠,使点C落在点F处,
∴DF=DC=AF=AD,FE=CE,
∴HC=GDAD,FGGD,
∴FH=GH﹣FG,EH=HC﹣ECEC,
在Rt△EFH中,
由勾股定理,得FH2+EH2=EF2,
即()2+(CE)2=CE2,
解得CE;
②FA=FB,如图,
过点F作GH⊥BC交AD于G,交BC于H,
则∠FAB=∠FBA,
∵四边形ABCD是正方形,AD,
∴四边形ABHG和四边形CDGH都是矩形,
∴GH=AB=DC=AD,∠BAD=∠ABC=∠AGF=∠BHF=90°,AG=BH,
∴∠FAG=∠FBH,
∴△FAG≌△FBH(AAS),
∴FG=FH,
∵将△CDE沿DE折叠,使点C落在点F处,
∴DF=DC=AD,EF=EC,
在Rt△DFH中,
由勾股定理,得DG,
∴CH,HE=CH﹣CECE,
在Rt△EFH中,
由勾股定理,得FH2+EH2=EF2,
即()2+(CE)2=CE2,
解得CE=1;
③BF=BA,此时点E与点B重合,不合题意,
综上,CE或1.
答案为:或1.
三.解答题(共8小题,满分75分)
16.解:(1)∵(x﹣2)(x+6)=0,
∴x﹣2=0或x+6=0,
解得:x=2或x=﹣6;
(2)∵3(x﹣5)2﹣2(x﹣5)=0,
∴(x﹣5)(3x﹣17)=0,
则x﹣5=0或3x﹣17=0,
解得:x=5或x.
17.解:(1)由根与系数关系得:m+n=2(a+1),mn=a2+5
依题意得:(m﹣1)(n﹣1)=28,
mn﹣m﹣n+1=28,
a2+5﹣2(a+1)+1=28,
a2﹣2a﹣24=0,
解得:a1=6,a2=﹣4,
由△≥0得:[﹣2(a+1)]2﹣4(a2+5)≥0,
a≥2,
∴a=6;
(2)分两种情况:
①当m=7或n=7时,即方程有一根为7,把x=7代入方程得:49﹣14(a+1)+a2+5=0,
整理得a2﹣14a+40=0,解得a1=10,a2=4,
当a=10时,x1+x2=2(a+1)=22,解得x2=15,而7+7<15,舍去;
当a=4时,x1+x2=2(a+1)=10,解得x2=3,则三角形周长为3+7+7=17;
②当m=n时,即方程有两个相等实根,x1=x2,则Δ=0,a=2,方程化为x2﹣6x+9=0,解得x1=x2=3,则3+3<7,舍去,
所以这个三角形的周长为17.
18.解:(1)∵抽样人数为2÷4%=50(人).
答案为:50;
(2)∵抽样人数为50人,
∴小说类的人数为50×40%=20(人),
补全条形统计图如下:
(3)∵抽样人数为50人,
∴动漫的百分比为12÷50=24%,
∴喜欢动漫类书籍的人数约为1600×24%=384(人),
答:估计这1600人中最喜欢动漫类书籍的有384人;
(4)画树状图如下:
由图知,共有12种等可能结果,其中都是“科技类”图书的有2种结果,
∴都是科技类图书的概率为.
19.解:(1)∵正比例函数y=﹣2x经过点A(﹣1,b),
∴b=﹣2×(﹣1)=2,
∴A(﹣1,2),
∵点A在反比例函数y图象上,
∴k=﹣1×2=﹣2;
(2)∵点C是x轴上的一点,△AOC的面积为3,
∴OC yA=3,即OC 2=3,
∴OC=3,
∴点C的坐标为(﹣3,0)或(3,0);
(3)∵正比例函数y=﹣2x与反比例函数y相交于点A(﹣1,2)和点B,
∴B(1,﹣2),
∵点M(a,m)在正比例函数y=﹣2x的图象上,点N(a,n)在反比例函数y的图象上,
∴MN∥y轴,
由图象可知,当m>n时,a的取值范围a<﹣1或0<a<1.
20.解析:(1)连结AD、OD,如图,
∵AB为⊙O的直径,
∴∠ADB=90°,即AD⊥BC,
∵AB=AC,
∴BD=CD,
而OA=OB,
∴OD为△ABC 的中位线,
∴OD∥AC,
∵EF是⊙O的切线;
∴OD⊥EF
OD∥AC,
∴EF⊥AC;
(2)设⊙O的半径为R,
∵OD∥AE,
∴△FOD∽△FAE,
∴,
∴,
∴R=4或(﹣3舍弃).
∴⊙O的半径为4.
21.解:(1)依题意,当球运行的水平距离为4m时,球达到最大高度,即x=0时,取得最大值,
将x=0,代入y=﹣0.09x2+3.86,
解得:y=3.86.
∴球达到的最大高度是3.86 m.
(2)设运动员跳离地面高度为hm,
将x=﹣4代入二次函数y=﹣0.09x2+3.86,
得h+1.84+0.3=﹣0.09×16+3.86,
解得h=0.28.
答:运动员跳离地面的高度是0.28 m.
22.解:(1)∵每箱消毒水降价1元,则可以多销售5箱,每箱降价x元,
∴日均销量多销售5x箱,
∴日均销量y关于x的函数关系式为y=5x+60.
(2)由题意得:
(26﹣x﹣12)(5x+60)=800,
整理得:x2﹣2x﹣8=0,
解得x1=4,x2=﹣2(不合题意,舍去);
∴要使日均利润为800元,则每箱应降价4元.
(3)由题意得5x+60≥85,
∴x≥5,
设销售这种消毒水的日均利润为w元,由题意得:
w=(26﹣x﹣12)(5x+60)+m(5x+60)
=(5x+60)(14﹣x+m)
=﹣5x2+10x+840+5mx+60m
=﹣5x2+(10+5m)x+840+60m,
∵﹣5<0,抛物线开口向下,
∴当x1时,w有最大值,
∵0<m≤6,
∴对称轴取值范围小于等于4,
∴当x=5时,w取最大值,即(5×5+60)(14﹣5+m)=1020,
解得m=3.
23.解:(1)∵∠A=30°,∠CDE=45°,
∴∠ABC=90°﹣30°=60°,∠E=90°﹣45°=45°,
∴∠EFB=∠ABC﹣∠E=60°﹣45°=15°;
(2)①∵CD∥AB,
∴∠ACD=∠A=30°,
∵∠ACD+∠ACE=∠DCE=90°,
∠ECB+∠ACE=∠ACB=90°,
∴∠ECB=∠ACD=30°;
②如图1,CE∥AB,∠ACE=∠A=30°,
∠ECB=∠ACB+∠ACE=90°+30°=120°;
如图2,DE∥AB时,延长CD交AB于F,
则∠BFC=∠D=45°,
在△BCF中,∠BCF=180°﹣∠B﹣∠BFC,
=180°﹣60°﹣45°=75°,
∴∠ECB=∠BCF+∠ECF=75°+90°=165°;
如图3,CD∥AB时,∠BCD=∠B=60°,
∠ECB=∠BCD+∠EDC=60°+90°=150°;
如图4,CE∥AB时,∠ECB=∠B=60°,
如图5,DE∥AB或DE与AB在同一条直线上时,∠ECB=60°﹣45°=15°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
