2025年中考数学几何辅助线解题方法第17 招 遇见线段等倍分,移转放缩找窍门(含解析)
文档属性
| 名称 | 2025年中考数学几何辅助线解题方法第17 招 遇见线段等倍分,移转放缩找窍门(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 518.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-13 00:00:00 | ||
图片预览




文档简介
第17 招 遇见线段等倍分,移转放缩找窍门
在题目给出的条件中,若当涉及的线段较为分散,但有相等,或倍、分的信息时,往往要巧妙地将有关线段进行平移、旋转、放缩,即过某点作平行于另一线段的平行线,或在一线段上截取一段等于另一段的若干倍,或将一线段绕某点旋转到另一位置,利用平移或旋转的关系将它们集结于某一特殊的图形之中,使之出现全等形、相似形或等腰三角形,由此获得解题思路.此招辅助线我们可将它表述为:
遇见线段等倍分,移转放缩找窍门.
易知,当线段换成角时,同样有:遇见角角等倍分,移转割补找窍门.
例1 如图17-1所示,已知△ABC是等腰三角形,D,E分别是腰AB及AC的延长线上的点,且BD=CE,连接DE交BC 于点G,求证:DE 被BC 平分.
解析 证法1 过点 D作DF∥AC交BC 于点F,(遇见线段等倍分,移转放缩找窍门)
如图 17-2 所示,则 ∠B=∠ACB=∠DFB,∴DB=DF.
在△DFG与△ECG中,
∵DF=DB=EC,∠1=∠2,∠3=∠4,
∴△DFG≌△ECG.
∴DG=EG,即DE被BC平分.
证法2 过点 D作DF∥BC,交AC于点F,如图17-3所示.
(遇见线段等倍分,移转放缩找窍门)
可得∠1=∠2=∠3=∠4,
∴AD=AF,
从而有FC=DB=CE.
在△EFD中,CG∥FD且CG过EF 的中点C,
则 CG 为△EDF 的中位线.(中点、中线想中位线)
故G为DE 的中点,所以 DE 被BC 平分.
证法3 过点E作EH∥BC,交AB的延长线于点 H,如图17-4所示.
(遇见线段等倍分,移转放缩找窍门)
可得∠1=∠2=∠3=∠AEH,
∴AH=AE.
又AB=AC,从而 BH=CE=DB.
在△EHD中,BG∥EH且BG 过DH 的中点B,
则 BG为△EDH的中位线.
(中点、中线想中位线,延线或作平行线)
故G为DE 的中点,所以 DE 被BC 平分.
证法4 过点G作GH∥BA,交AC于点H,如图17-5所示.
(遇见线段等倍分,移转放缩找窍门)
设 HG=x,则易证 HG=HC=x.
又设DB=EC=y,AB=AC=b,
由GH∥DA,得 则
∴bx+ xy= bx+ by-xy-y ,
故
从而可得
即G是DE 的中点,所以 DE 被BC 平分.
证法5 设点 D到BC边的距离为h,如图17-6 所示,则h=BD· sin B.
∵∠B=∠GCA,又∠ 设点E到BC 边的距离为h',
贝 ①又∠1=∠2,于是,同理可得
由①②,得 故
又BD=CE,所以GD=GE,即DE被BC 平分.
点评 从本例的证明可知,辅助线作的不同,证法也有所不同.证法1是从全等的角度来思考的.证法2 与证法3 相当,都是作 BC的平行线,利用三角形的中位线来分析的,不同的是证法2注重将CE平移,向BD靠拢.证法3注重将BD向下移.体现了“遇见线段等倍分,移转放缩找窍门”的战术思想.证法4侧重于计算推理的思维.证法5是从面积的比来探究的.所有这些证法都是常见的基本思路.不难得知,利用全等三角形的方法亦可按图17-7与图17-8所示的方法添加辅助线.读者不妨试试.
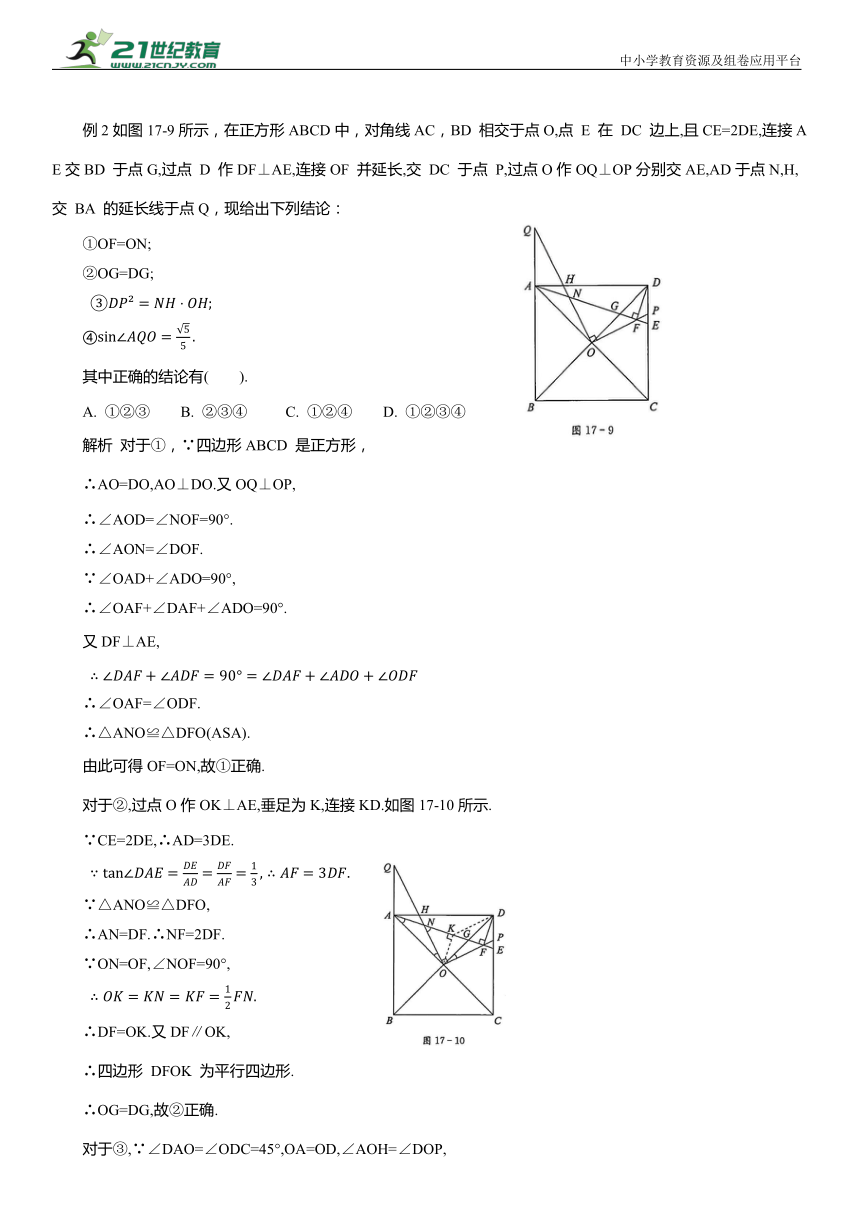
例2如图17-9所示,在正方形ABCD中,对角线AC,BD 相交于点O,点 E 在 DC 边上,且CE=2DE,连接AE交BD 于点G,过点 D 作DF⊥AE,连接OF 并延长,交 DC 于点 P,过点O作OQ⊥OP分别交AE,AD于点N,H,交 BA 的延长线于点Q,现给出下列结论:
①OF=ON;
②OG=DG;
④
其中正确的结论有( ).
A. ①②③ B. ②③④ C. ①②④ D. ①②③④
解析 对于①,∵四边形ABCD 是正方形,
∴AO=DO,AO⊥DO.又OQ⊥OP,
∴∠AOD=∠NOF=90°.
∴∠AON=∠DOF.
∵∠OAD+∠ADO=90°,
∴∠OAF+∠DAF+∠ADO=90°.
又DF⊥AE,
∴∠OAF=∠ODF.
∴△ANO≌△DFO(ASA).
由此可得OF=ON,故①正确.
对于②,过点O作OK⊥AE,垂足为K,连接KD.如图17-10所示.
∵CE=2DE,∴AD=3DE.
∵△ANO≌△DFO,
∴AN=DF.∴NF=2DF.
∵ON=OF,∠NOF=90°,
∴DF=OK.又DF∥OK,
∴四边形 DFOK 为平行四边形.
∴OG=DG,故②正确.
对于③,∵∠DAO=∠ODC=45°,OA=OD,∠AOH=∠DOP,
∴△AOH≌△DOP(ASA).
∴AH=DP.
(遇见线段等倍分,移转放缩找窍门)
∠AHN=∠AHO,∴△AHN∽△OHA.
故③正确.
对于④,过点 E作EM⊥AC,垂足为 M,如图17-11所示.
设CD=3,则
且有
又易知 在 Rt△AEM中,
故④正确.
另解 ∵∠NAO+∠AON=∠ANQ=45°,∠AQO+∠AON=∠BAO=45°,
∴∠NAO=∠AQO.
∵OG=GD,∴AO=2OG.
故有
故④正确.
故选 D.
点评 本题涉及知识点较多,主要考查正方形的性质,全等三角形、相似三角形的判定和性质、等腰三角形的判定和性质、锐角三角函数,对逻辑推理能力要求较高.对于①,关键是能否意识到是将AO顺时针旋转90°到 DO,将ON 顺时针旋转90°到 OP,挖掘∠AON=∠DOF,进而挖掘△ANO≌△DFO,证得OF=ON;对于②,关键是能否作辅助线OK,将所要证的OG=DG移到转证DF=OK;对于③关键是能否先挖掘△AOH≌△DOP,得出AH=DP,进而转移到证明 ,再挖掘△AHN∽△OHA,并利用相似比来完成推证;对于④,两种解法都注重了角的转移与线段的计算.易知,本题对四个结论的推断都充分体现了“遇见线段等倍分,移转放缩找窍门”的战术思想.
例3 如图17-12 所示,已知在正方形 ABCD中,点E在AB上,且CE=AD+AE,F 是AB 的中点,求证:∠DCE=2∠BCF.
解析证法1 延长CD至点G,使DG=AE,连接EG,交AD于点 H,如图17-13所示,
则有∠DCE=∠3+∠2.
(遇见角角等倍分,移转割补找窍门)
CG=CD+DG=AD+AE=CE.
在Rt△CGH与Rt△CGH中,
中小学教育资源及组卷应用平台
(CHANCC∠ANEN). ∴∴Rt△DHG≌Rt△AHE.(AAS)
∴DH=AH,GH=EH,即H为EG与AD 的中点.
∴CH⊥EG,∠DCH=∠ECH,即∠2=∠3.
∴∠2=∠1,
由此可得∠DCE=2∠BCF.
证法2 延长EA至点M,使MA=AD,连接CM,如图17-14所示,(遇见角角等倍分,移转割补找窍门)
则有∠DCE=∠3+∠2,
且EM=AE+AM=AD+AE=CE.
∴△EMC为等腰三角形.∴∠3=∠4.
∵CD∥AM,∴∠2=∠4,AH=DH.
从而可得∠3=∠2=∠4,
∴∠1=∠4.
由此可得∠1=∠4=∠2.
∴∠DCE=2∠BCF.
点评 本题主要考查角的倍分问题,考查构造辅助线将角转移的探究能力.两种证法都凸显了“遇见角角等倍分,移转割补找窍门”的战术思想,也体现了“边边有加减,常把一边延”的解题策略.
例4 如图17-15 所示,凸四边形ABCD 的对角线AC,BD交于一点 E,若∠ABD=35°,∠ACB=40°,∠ADB=20°,∠ACD=70°,则∠AEB=( ).
A. 60° B. 65°
C.70° D. 75°
解析解法1 如图17-16 所示,延长AC到点F,使CF=CD,
连接BF,DF,则∠AFD=∠CDF.
(遇见角角等倍分,移转割补找窍门)
∵∠ACD=∠AFD+∠CDF=70°,
∵∠ABD=35°,∠AEB=∠DEF,
(引线造角望相似,通性通法灵活使)
又∠AED=∠BEF,
∴△AED∽△BEF.
∴∠AFB=∠ADB.
∵∠ADB=20°,∴∠AFB=20°.
∵∠ACB=∠AFB+∠CBF=40°,
∴∠CBF=20°.∴CB=CF=CD.
故选 D.
解法2 如图17-16 所示,延长AC到F,使CF=CB,连接BF,DF,则∠AFB=∠CBF.(遇见角角等倍分,移转割补找窍门)
∵∠ADB=20°=∠AFB,∴A,B,F,D四点共圆.(同侧视角等,四点可构圆)
∴CF=CD.又CF=CB,所以点C为圆心,且AF 为直径.
∴∠ABF=90°.(等圆周角等弧弦,直径直角互关联)
故选 D.
解法3 如图 17-17 所示.过点 C 作∠ACB的平分线CM,交BD于点M,连接AM.
(遇见角角等倍分,移转割补找窍门)
由题意易知∠ADM=∠ACM=20°,
∴A,M,C,D四点共圆.
(同侧视角等,四点可构圆)
∴∠AMD=∠ACD=70°.(等圆周角等弧弦)
又∠ABM=35°,
∴∠MAB=35°.∴AM=BM.
过点 M作MP⊥AC,垂足为 P,MQ⊥BC,垂足为Q,由角平分线性质得MP=MQ,
∴△APM≌△BQM(HL).
∴∠MAP=∠MBQ,从而∠BAC=∠ABC.
∴△ABC为等腰三角形.
又∠ACB=40°,∴∠CAB=70°.
故选 D.
解法4 如图17-18所示.在 BD上取一点N,连接AN,CN,使∠DAN=20°,
则AN=DN.(遇见角角等倍分,移转割补找窍门)
又∠ADN=20°,∴∠ANB=∠ACB=40°.
∴A,N,C,B四点共圆.
(同侧视角等,四点可构圆)
∴∠ABN=∠ACN=35°.(等圆周角等弧弦)
又∠ACD=70°,∴CN 为∠ACD的平分线.
过点 N作NS⊥DC,垂足为S,NR⊥AC,垂足为R,由角平分线性质得 NS=NR,又AN=DN,
∴△ANR≌△DNS(HL).
∴∠NAR=∠NDS,从而∠CAD=∠CDA.又∠ACD=70°,∴∠CDA=55°.
∠AEB=∠DEC=180°-∠ACD-∠CDN=75°.
故选 D.
点评 本题考查了相似三角形的判定与性质、四点共圆性质,考查了添加辅助线将角转移的基本方法,对创新思维能力的要求较高.解法1通过观察∠ACD=70°、∠ABD=35°、∠ACB=40°、∠ADB= 20°四角,发现它们具有二倍角的关系,由此想到“遇见角角等倍分,移转割补找窍门”的战术,设法将70°角分割成两个35°的角。在添加辅助线时,用延长AC,使CF=CD实现角的移转是一个较好的选择.具体做法是一作、二证,即先作∠DFA=35°,再证∠BFA=20°.解法2通过作∠BFA=20°,发现了∠AFB=∠ADB=20°,由此获得A,B,F,D四点共圆,进而得到AF为直径,是一种创造性的思维.解法3是通过作CM平分∠ACB,将40°分割成两个20°角,挖掘A,M,C,D 四点共圆,进而挖掘△ABC为等腰三角形,获得∠CDE=35°.解法4注重了将小角20°放大两倍成40°,与解法3相比只是说法不同而已,类似地,我们也可以点C为出发点,将∠ACD=70°的角转移来探究,读者不妨试试.
跟踪训练
1. 如图所示,在△ABC中,AD是BC边上的高,CE是AB 边上的中线,且 DC=BE,
求证:(1) 点D 在CE 的垂直平分线上.
(2)∠B=2∠BCE.
2. 如图所示,在梯形 ABCD 中, ,E为AB 上一点,且 点 F在CE 上,且
(1) 若CE平分 求证:(
(2)求证:
3. 已知在△ABC中.
(1) 如图1所示,E为BC的中点,延长AE到点F,使得FE=EA,连接 BF,直接写出 BF和AC 的关系.
(2)如图2所示,若AB=AC,E为AC上一点,过点C作BC 的垂线交BE 的延长线于点D,连接AD,若∠DAC=∠ABD,求证:AE=EC.
(3)如图3所示,点 D 在△ABC内部,且满足AD=BC,∠BAD= 点M在DC的延长线上,连接AM交BD 的延长线于点N,若N为AM的中点,求证:DM=AB.
答案
1. (1) 证明:连接ED,如图所示.
∵AD是△ABC边BC上的高,∴∠ADB=90°.
在 Rt△ADB中,DE是AB 边上的中线,
∵DC=BE,∴ED=DC.
由此可得点 D在CE 的垂直平分线上.
(2)∵ED=DC,∴∠DEC=∠ECD.
∵∠EDB=∠DEC+∠ECD=2∠BCE,∴∠B=2∠BCE.
2. (1) 由CD=CE,故可转移证 CE=2BE.
如图所示,连接AC,在△CDA 和△CEA中
∴△CDA≌△CEA(SSS).
∴∠DAC=∠EAC,∠DCA=∠ECA.∴∠ECA= ∠DCE.
∵AD∥BC,∠B=90°,∴∠DAB=90°,∠DAC=∠ACB.
∵∠DAC=∠EAC,∴∠BAC=∠ACB=45°.
∵CE平分∠DCB,∴∠DCE=∠BCE.
∵∠B=90°,CE=2BE,∴CD=2BE.
(2) 由(1),得△CDA≌△CEA,∴∠ADC=∠AEC.
∵∠ADC=∠CFD,∴∠AEC=∠CFD.∴AE∥DF.
由(1),得∠DAB=90°,∴∠ADF=90°.
∵∠DCE+∠CFD+∠CDF=180°,
∴ C.
又
3. (1)结论:BF=AC,BF∥AC.
理由:在图1中,
∵AE=FE,∠AEC=∠FEB,EC=EB,
∴△AEC≌△FEB(SAS).
∴AC=FB,∠C=∠FBE.∴AC∥BF.
(2)证明:在图2中,过点A作AH⊥BC,垂足为 H,过点 C作( 交AD的延长线于T.
∵AB∥CT,∴∠BAE=∠ACT.
∵AB=CA,∠ABE=∠CAT,
∴△ABE≌△CAT(ASA).
∴AE=CT,∠AEB=∠T.
∵∠DEC=∠AEB,∴∠DEC=∠T.
∵AH⊥BC,CD⊥CB,
∴AH∥CD.∴∠CAH=∠ACD.
∵AB=AC,AH⊥BC,
∴∠BAC=2∠CAH.∴∠ACT=2∠ACD.
∴∠DCE=∠DCT.
∵CD=CD,∴△CDE≌△CDT(AAS).
∴CE=CT.∴AE=EC.
(3)证明:过点 M作MT∥AB交BN 的延长线于点 T,. )交BT于点G,在 MT上取一点K,使得MK=CD,连接GK.如图3所示.
∵AB∥MT,∴∠ABN=∠T.
∵∠ANB=MNT,AN=NM,
∴△ANB≌△MNT(AAS).
∵AD∥MG,∴∠ADN=∠MGN.
∴△AND≌△MNG(AAS).
∴AD=MG,DN=NG.
∴BD=GT.
∵∠BAN=∠AMT,∠DAN=∠GMN,
∴∠BAD=∠GMT.
∵∠BAD=∠BCD,∴∠BCD=∠GMK.
∵AD=BC,AD=GM,∴CB=MG.
又CD=MK,∴△BCD≌△GMK(SAS).
∴GK=BD,∠BDC=∠MKG.∴GK=GT,∠MDT=∠GKT.
∴∠GKT=∠T.∴∠MDT=∠T.∴DM=MT.
∵AB=MT,∴DM=AB.
在题目给出的条件中,若当涉及的线段较为分散,但有相等,或倍、分的信息时,往往要巧妙地将有关线段进行平移、旋转、放缩,即过某点作平行于另一线段的平行线,或在一线段上截取一段等于另一段的若干倍,或将一线段绕某点旋转到另一位置,利用平移或旋转的关系将它们集结于某一特殊的图形之中,使之出现全等形、相似形或等腰三角形,由此获得解题思路.此招辅助线我们可将它表述为:
遇见线段等倍分,移转放缩找窍门.
易知,当线段换成角时,同样有:遇见角角等倍分,移转割补找窍门.
例1 如图17-1所示,已知△ABC是等腰三角形,D,E分别是腰AB及AC的延长线上的点,且BD=CE,连接DE交BC 于点G,求证:DE 被BC 平分.
解析 证法1 过点 D作DF∥AC交BC 于点F,(遇见线段等倍分,移转放缩找窍门)
如图 17-2 所示,则 ∠B=∠ACB=∠DFB,∴DB=DF.
在△DFG与△ECG中,
∵DF=DB=EC,∠1=∠2,∠3=∠4,
∴△DFG≌△ECG.
∴DG=EG,即DE被BC平分.
证法2 过点 D作DF∥BC,交AC于点F,如图17-3所示.
(遇见线段等倍分,移转放缩找窍门)
可得∠1=∠2=∠3=∠4,
∴AD=AF,
从而有FC=DB=CE.
在△EFD中,CG∥FD且CG过EF 的中点C,
则 CG 为△EDF 的中位线.(中点、中线想中位线)
故G为DE 的中点,所以 DE 被BC 平分.
证法3 过点E作EH∥BC,交AB的延长线于点 H,如图17-4所示.
(遇见线段等倍分,移转放缩找窍门)
可得∠1=∠2=∠3=∠AEH,
∴AH=AE.
又AB=AC,从而 BH=CE=DB.
在△EHD中,BG∥EH且BG 过DH 的中点B,
则 BG为△EDH的中位线.
(中点、中线想中位线,延线或作平行线)
故G为DE 的中点,所以 DE 被BC 平分.
证法4 过点G作GH∥BA,交AC于点H,如图17-5所示.
(遇见线段等倍分,移转放缩找窍门)
设 HG=x,则易证 HG=HC=x.
又设DB=EC=y,AB=AC=b,
由GH∥DA,得 则
∴bx+ xy= bx+ by-xy-y ,
故
从而可得
即G是DE 的中点,所以 DE 被BC 平分.
证法5 设点 D到BC边的距离为h,如图17-6 所示,则h=BD· sin B.
∵∠B=∠GCA,又∠ 设点E到BC 边的距离为h',
贝 ①又∠1=∠2,于是,同理可得
由①②,得 故
又BD=CE,所以GD=GE,即DE被BC 平分.
点评 从本例的证明可知,辅助线作的不同,证法也有所不同.证法1是从全等的角度来思考的.证法2 与证法3 相当,都是作 BC的平行线,利用三角形的中位线来分析的,不同的是证法2注重将CE平移,向BD靠拢.证法3注重将BD向下移.体现了“遇见线段等倍分,移转放缩找窍门”的战术思想.证法4侧重于计算推理的思维.证法5是从面积的比来探究的.所有这些证法都是常见的基本思路.不难得知,利用全等三角形的方法亦可按图17-7与图17-8所示的方法添加辅助线.读者不妨试试.
例2如图17-9所示,在正方形ABCD中,对角线AC,BD 相交于点O,点 E 在 DC 边上,且CE=2DE,连接AE交BD 于点G,过点 D 作DF⊥AE,连接OF 并延长,交 DC 于点 P,过点O作OQ⊥OP分别交AE,AD于点N,H,交 BA 的延长线于点Q,现给出下列结论:
①OF=ON;
②OG=DG;
④
其中正确的结论有( ).
A. ①②③ B. ②③④ C. ①②④ D. ①②③④
解析 对于①,∵四边形ABCD 是正方形,
∴AO=DO,AO⊥DO.又OQ⊥OP,
∴∠AOD=∠NOF=90°.
∴∠AON=∠DOF.
∵∠OAD+∠ADO=90°,
∴∠OAF+∠DAF+∠ADO=90°.
又DF⊥AE,
∴∠OAF=∠ODF.
∴△ANO≌△DFO(ASA).
由此可得OF=ON,故①正确.
对于②,过点O作OK⊥AE,垂足为K,连接KD.如图17-10所示.
∵CE=2DE,∴AD=3DE.
∵△ANO≌△DFO,
∴AN=DF.∴NF=2DF.
∵ON=OF,∠NOF=90°,
∴DF=OK.又DF∥OK,
∴四边形 DFOK 为平行四边形.
∴OG=DG,故②正确.
对于③,∵∠DAO=∠ODC=45°,OA=OD,∠AOH=∠DOP,
∴△AOH≌△DOP(ASA).
∴AH=DP.
(遇见线段等倍分,移转放缩找窍门)
∠AHN=∠AHO,∴△AHN∽△OHA.
故③正确.
对于④,过点 E作EM⊥AC,垂足为 M,如图17-11所示.
设CD=3,则
且有
又易知 在 Rt△AEM中,
故④正确.
另解 ∵∠NAO+∠AON=∠ANQ=45°,∠AQO+∠AON=∠BAO=45°,
∴∠NAO=∠AQO.
∵OG=GD,∴AO=2OG.
故有
故④正确.
故选 D.
点评 本题涉及知识点较多,主要考查正方形的性质,全等三角形、相似三角形的判定和性质、等腰三角形的判定和性质、锐角三角函数,对逻辑推理能力要求较高.对于①,关键是能否意识到是将AO顺时针旋转90°到 DO,将ON 顺时针旋转90°到 OP,挖掘∠AON=∠DOF,进而挖掘△ANO≌△DFO,证得OF=ON;对于②,关键是能否作辅助线OK,将所要证的OG=DG移到转证DF=OK;对于③关键是能否先挖掘△AOH≌△DOP,得出AH=DP,进而转移到证明 ,再挖掘△AHN∽△OHA,并利用相似比来完成推证;对于④,两种解法都注重了角的转移与线段的计算.易知,本题对四个结论的推断都充分体现了“遇见线段等倍分,移转放缩找窍门”的战术思想.
例3 如图17-12 所示,已知在正方形 ABCD中,点E在AB上,且CE=AD+AE,F 是AB 的中点,求证:∠DCE=2∠BCF.
解析证法1 延长CD至点G,使DG=AE,连接EG,交AD于点 H,如图17-13所示,
则有∠DCE=∠3+∠2.
(遇见角角等倍分,移转割补找窍门)
CG=CD+DG=AD+AE=CE.
在Rt△CGH与Rt△CGH中,
中小学教育资源及组卷应用平台
(CHANCC∠ANEN). ∴∴Rt△DHG≌Rt△AHE.(AAS)
∴DH=AH,GH=EH,即H为EG与AD 的中点.
∴CH⊥EG,∠DCH=∠ECH,即∠2=∠3.
∴∠2=∠1,
由此可得∠DCE=2∠BCF.
证法2 延长EA至点M,使MA=AD,连接CM,如图17-14所示,(遇见角角等倍分,移转割补找窍门)
则有∠DCE=∠3+∠2,
且EM=AE+AM=AD+AE=CE.
∴△EMC为等腰三角形.∴∠3=∠4.
∵CD∥AM,∴∠2=∠4,AH=DH.
从而可得∠3=∠2=∠4,
∴∠1=∠4.
由此可得∠1=∠4=∠2.
∴∠DCE=2∠BCF.
点评 本题主要考查角的倍分问题,考查构造辅助线将角转移的探究能力.两种证法都凸显了“遇见角角等倍分,移转割补找窍门”的战术思想,也体现了“边边有加减,常把一边延”的解题策略.
例4 如图17-15 所示,凸四边形ABCD 的对角线AC,BD交于一点 E,若∠ABD=35°,∠ACB=40°,∠ADB=20°,∠ACD=70°,则∠AEB=( ).
A. 60° B. 65°
C.70° D. 75°
解析解法1 如图17-16 所示,延长AC到点F,使CF=CD,
连接BF,DF,则∠AFD=∠CDF.
(遇见角角等倍分,移转割补找窍门)
∵∠ACD=∠AFD+∠CDF=70°,
∵∠ABD=35°,∠AEB=∠DEF,
(引线造角望相似,通性通法灵活使)
又∠AED=∠BEF,
∴△AED∽△BEF.
∴∠AFB=∠ADB.
∵∠ADB=20°,∴∠AFB=20°.
∵∠ACB=∠AFB+∠CBF=40°,
∴∠CBF=20°.∴CB=CF=CD.
故选 D.
解法2 如图17-16 所示,延长AC到F,使CF=CB,连接BF,DF,则∠AFB=∠CBF.(遇见角角等倍分,移转割补找窍门)
∵∠ADB=20°=∠AFB,∴A,B,F,D四点共圆.(同侧视角等,四点可构圆)
∴CF=CD.又CF=CB,所以点C为圆心,且AF 为直径.
∴∠ABF=90°.(等圆周角等弧弦,直径直角互关联)
故选 D.
解法3 如图 17-17 所示.过点 C 作∠ACB的平分线CM,交BD于点M,连接AM.
(遇见角角等倍分,移转割补找窍门)
由题意易知∠ADM=∠ACM=20°,
∴A,M,C,D四点共圆.
(同侧视角等,四点可构圆)
∴∠AMD=∠ACD=70°.(等圆周角等弧弦)
又∠ABM=35°,
∴∠MAB=35°.∴AM=BM.
过点 M作MP⊥AC,垂足为 P,MQ⊥BC,垂足为Q,由角平分线性质得MP=MQ,
∴△APM≌△BQM(HL).
∴∠MAP=∠MBQ,从而∠BAC=∠ABC.
∴△ABC为等腰三角形.
又∠ACB=40°,∴∠CAB=70°.
故选 D.
解法4 如图17-18所示.在 BD上取一点N,连接AN,CN,使∠DAN=20°,
则AN=DN.(遇见角角等倍分,移转割补找窍门)
又∠ADN=20°,∴∠ANB=∠ACB=40°.
∴A,N,C,B四点共圆.
(同侧视角等,四点可构圆)
∴∠ABN=∠ACN=35°.(等圆周角等弧弦)
又∠ACD=70°,∴CN 为∠ACD的平分线.
过点 N作NS⊥DC,垂足为S,NR⊥AC,垂足为R,由角平分线性质得 NS=NR,又AN=DN,
∴△ANR≌△DNS(HL).
∴∠NAR=∠NDS,从而∠CAD=∠CDA.又∠ACD=70°,∴∠CDA=55°.
∠AEB=∠DEC=180°-∠ACD-∠CDN=75°.
故选 D.
点评 本题考查了相似三角形的判定与性质、四点共圆性质,考查了添加辅助线将角转移的基本方法,对创新思维能力的要求较高.解法1通过观察∠ACD=70°、∠ABD=35°、∠ACB=40°、∠ADB= 20°四角,发现它们具有二倍角的关系,由此想到“遇见角角等倍分,移转割补找窍门”的战术,设法将70°角分割成两个35°的角。在添加辅助线时,用延长AC,使CF=CD实现角的移转是一个较好的选择.具体做法是一作、二证,即先作∠DFA=35°,再证∠BFA=20°.解法2通过作∠BFA=20°,发现了∠AFB=∠ADB=20°,由此获得A,B,F,D四点共圆,进而得到AF为直径,是一种创造性的思维.解法3是通过作CM平分∠ACB,将40°分割成两个20°角,挖掘A,M,C,D 四点共圆,进而挖掘△ABC为等腰三角形,获得∠CDE=35°.解法4注重了将小角20°放大两倍成40°,与解法3相比只是说法不同而已,类似地,我们也可以点C为出发点,将∠ACD=70°的角转移来探究,读者不妨试试.
跟踪训练
1. 如图所示,在△ABC中,AD是BC边上的高,CE是AB 边上的中线,且 DC=BE,
求证:(1) 点D 在CE 的垂直平分线上.
(2)∠B=2∠BCE.
2. 如图所示,在梯形 ABCD 中, ,E为AB 上一点,且 点 F在CE 上,且
(1) 若CE平分 求证:(
(2)求证:
3. 已知在△ABC中.
(1) 如图1所示,E为BC的中点,延长AE到点F,使得FE=EA,连接 BF,直接写出 BF和AC 的关系.
(2)如图2所示,若AB=AC,E为AC上一点,过点C作BC 的垂线交BE 的延长线于点D,连接AD,若∠DAC=∠ABD,求证:AE=EC.
(3)如图3所示,点 D 在△ABC内部,且满足AD=BC,∠BAD= 点M在DC的延长线上,连接AM交BD 的延长线于点N,若N为AM的中点,求证:DM=AB.
答案
1. (1) 证明:连接ED,如图所示.
∵AD是△ABC边BC上的高,∴∠ADB=90°.
在 Rt△ADB中,DE是AB 边上的中线,
∵DC=BE,∴ED=DC.
由此可得点 D在CE 的垂直平分线上.
(2)∵ED=DC,∴∠DEC=∠ECD.
∵∠EDB=∠DEC+∠ECD=2∠BCE,∴∠B=2∠BCE.
2. (1) 由CD=CE,故可转移证 CE=2BE.
如图所示,连接AC,在△CDA 和△CEA中
∴△CDA≌△CEA(SSS).
∴∠DAC=∠EAC,∠DCA=∠ECA.∴∠ECA= ∠DCE.
∵AD∥BC,∠B=90°,∴∠DAB=90°,∠DAC=∠ACB.
∵∠DAC=∠EAC,∴∠BAC=∠ACB=45°.
∵CE平分∠DCB,∴∠DCE=∠BCE.
∵∠B=90°,CE=2BE,∴CD=2BE.
(2) 由(1),得△CDA≌△CEA,∴∠ADC=∠AEC.
∵∠ADC=∠CFD,∴∠AEC=∠CFD.∴AE∥DF.
由(1),得∠DAB=90°,∴∠ADF=90°.
∵∠DCE+∠CFD+∠CDF=180°,
∴ C.
又
3. (1)结论:BF=AC,BF∥AC.
理由:在图1中,
∵AE=FE,∠AEC=∠FEB,EC=EB,
∴△AEC≌△FEB(SAS).
∴AC=FB,∠C=∠FBE.∴AC∥BF.
(2)证明:在图2中,过点A作AH⊥BC,垂足为 H,过点 C作( 交AD的延长线于T.
∵AB∥CT,∴∠BAE=∠ACT.
∵AB=CA,∠ABE=∠CAT,
∴△ABE≌△CAT(ASA).
∴AE=CT,∠AEB=∠T.
∵∠DEC=∠AEB,∴∠DEC=∠T.
∵AH⊥BC,CD⊥CB,
∴AH∥CD.∴∠CAH=∠ACD.
∵AB=AC,AH⊥BC,
∴∠BAC=2∠CAH.∴∠ACT=2∠ACD.
∴∠DCE=∠DCT.
∵CD=CD,∴△CDE≌△CDT(AAS).
∴CE=CT.∴AE=EC.
(3)证明:过点 M作MT∥AB交BN 的延长线于点 T,. )交BT于点G,在 MT上取一点K,使得MK=CD,连接GK.如图3所示.
∵AB∥MT,∴∠ABN=∠T.
∵∠ANB=MNT,AN=NM,
∴△ANB≌△MNT(AAS).
∵AD∥MG,∴∠ADN=∠MGN.
∴△AND≌△MNG(AAS).
∴AD=MG,DN=NG.
∴BD=GT.
∵∠BAN=∠AMT,∠DAN=∠GMN,
∴∠BAD=∠GMT.
∵∠BAD=∠BCD,∴∠BCD=∠GMK.
∵AD=BC,AD=GM,∴CB=MG.
又CD=MK,∴△BCD≌△GMK(SAS).
∴GK=BD,∠BDC=∠MKG.∴GK=GT,∠MDT=∠GKT.
∴∠GKT=∠T.∴∠MDT=∠T.∴DM=MT.
∵AB=MT,∴DM=AB.
同课章节目录
