2025年中考数学几何辅助线解题方法第18招 等积转换出妙招,巧在活用底与高(含解析)
文档属性
| 名称 | 2025年中考数学几何辅助线解题方法第18招 等积转换出妙招,巧在活用底与高(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 577.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-13 15:49:18 | ||
图片预览




文档简介
第18招 等积转换出妙招,巧在活用底与高
在题目给出的条件中,若当涉及三角形的面积或面积比时,往往离不开等积变换思想方法的运用.这是因为当三角形的高线一定时,它的底在底边所在直线上作任意移动,其面积不变,即等底共高的三角形面积相等.进而得到:等高的三角形的面积比等于其底的比;等底的三角形的面积比等于其高的比.由于三角形的任何一边都可以作为它的底.因此,三角形是等积变形中最活跃的图形.当把所研究的图形恰当地分解或组合成三角形,并根据题设的条件选定其底、高,巧用等积转换的思想方法来分析,往往可收到出奇制胜、事半功倍之效.此招辅助线我们可将它表述为:
等积转换出妙招,巧在活用底与高.
例1 在 Rt△ABC中,已知∠C=90°,AC=3,BC=4,以点C为圆心,r为半径作圆,要使圆与线段 AB有两个公共点,则r的值不可能是( ).
C. 3
解析 如图18-1所示,作CD⊥AB,垂足为D.(巧在活用底与高)
∵∠C=90°,AC=3,BC=4,
(等积转换出妙招)
即圆心C到AB的距离
因为AC所以以C为圆心, 或4为半径所作的圆与斜边 AB 只有一个公共点.
由此可得,要使⊙C与斜边AB 有两个公共点,则r的取值范围是
故选 D.
点评 此题考查了直线与圆的位置关系、直角三角形的性质,考查了等积转换思想的运用.解题关键是正确理解题意.这里先挖掘圆与线段AB有两个交点时r所在的范围,再由选项确定解是解题的基本思想.当然对本题的求解,亦可用排除法分析.如当r=3时有两个交点,当r>3时只能有一个交点,或没有交点.再结合选项即可得到解答.
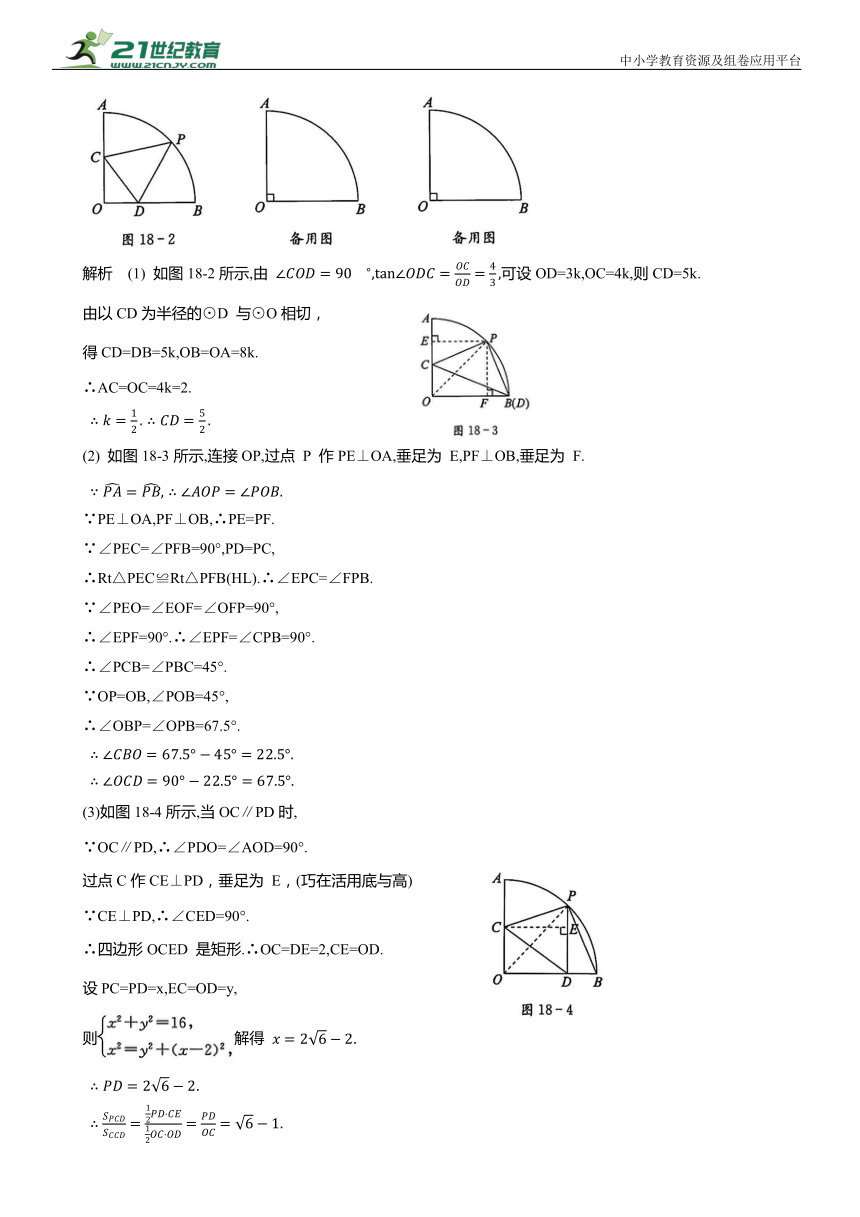
例2如图18-2所示,已知扇形 AOB的半径OA=4,∠AOB=90°,点C,D分别在半径OA,OB上(点C不与点A重合),连接CD.点 P 是弧AB 上一点,PC=PD.
(1) 当 以 CD 为半径的⊙D 与⊙O 相切时,求 CD的长.
(2) 当点 D与点B 重合,点 P 为弧AB 的中点时,求∠OCD的度数.
(3) 如果OC=2,且四边形ODPC 是梯形,求 的值.
解析 (1) 如图18-2所示,由 可设OD=3k,OC=4k,则CD=5k.
由以CD为半径的⊙D 与⊙O相切,
得CD=DB=5k,OB=OA=8k.
∴AC=OC=4k=2.
(2) 如图18-3所示,连接OP,过点 P 作PE⊥OA,垂足为 E,PF⊥OB,垂足为 F.
∵PE⊥OA,PF⊥OB,∴PE=PF.
∵∠PEC=∠PFB=90°,PD=PC,
∴Rt△PEC≌Rt△PFB(HL).∴∠EPC=∠FPB.
∵∠PEO=∠EOF=∠OFP=90°,
∴∠EPF=90°.∴∠EPF=∠CPB=90°.
∴∠PCB=∠PBC=45°.
∵OP=OB,∠POB=45°,
∴∠OBP=∠OPB=67.5°.
(3)如图18-4所示,当OC∥PD时,
∵OC∥PD,∴∠PDO=∠AOD=90°.
过点C作CE⊥PD,垂足为 E,(巧在活用底与高)
∵CE⊥PD,∴∠CED=90°.
∴四边形OCED 是矩形.∴OC=DE=2,CE=OD.
设PC=PD=x,EC=OD=y,
则解得
如图18-5所示,当PC∥OD时,∵PC∥OD,∴∠COD=∠OCE=∠CED=90°.
过点 D作DE⊥PC,垂足为 E,(巧在活用底与高)
∴四边形OCED 是矩形.
∴OC=DE=2,CE=OD.
∵OP=4,OC=2,
综上所述 的值为 或
点评 本题综合性较强,涉及的知识点较多,主要考查了两圆的位置关系,解直角三角形,等腰三角形的性质,梯形的性质等知识,考查了分类讨论思想、等积转换思想.解题的关键是要正确地添加常用辅助线得到等高的三角形.属于中考压轴题.
例3 (1)探索发现 如图18-6 所示,在△ABC中,点 D 在边BC上,△ABD与△ADC 的面积分别记为S 与S ,试判断 的数量关系,并说明理由.
(2) 阅读分析 小东遇到这样一个问题:如图18-7 所示,在Rt△ABC中,AB=AC,∠BAC=90°,射线AM交 BC于点 D,点 E,F在AM上,且∠CEM=∠BFM=90°,试判断BF,CE,EF 三条线段之间的数量关系.
小东利用一对全等三角形,经过推理使问题得以解决.
填空:①在图18-7中的一对全等三角形为 与 .
② BF,CE,EF三条线段之间的数量关系为 .
(3)类比探究 如图18-8所示,在四边形ABCD中,AB=AD,AC与BD 交于点O,点E,F在射线AC 上,且∠BCF=∠DEF=∠BAD.
① 判断BC,DE,CE三条线段之间的数量关系,并说明理由.
② 若OD=3OB,△AED的面积为2,直接写出四边形 ABCD的面积.
解析 (1)结论:
理由:如图18-9所示,作AH⊥BC,垂足为 H.(巧在活用底与高)
(2) 如图18-7所示,
∵∠CEM=∠BFM=∠BAC=90°,
∴∠AEC=∠AFB=90°.
∴∠BAF+∠CAE=90°,∠CAE+∠ACE=90°,从而有∠BAF=∠ACE.
∵AB=AC,∴△AFB≌△CEA(AAS).
∴AF=CE,BF=AE.
∴CE=AF=AE+EF=BF+EF.
故答案为:①△AFB,△CEA.②CE=EF+BF.
(3)①在图18-8中,结论:DE=BC+CE.
理由:∵∠BCF=∠DEF,∴∠ACB=∠DEA.
∵∠BCF=∠BAD,∠BCF=∠ABC+∠BAC,∠BAD=∠BAC+∠DAE,
∴∠ABC=∠DAE.
∵AB=DA,∴△ABC≌△DAE(ASA).
∴BC=AE,AC=DE.
∵AC=AE+CE,∴DE=BC+CE.
②解法1 因为OD=3OB,
由(1)的结论得S△AOD=3S△ABO,S△ωD=3S△ωB,
∴S△ACD=3S△ABC.
∵△ABC≌△DEA,所以S△ABC=S△ADE=2.
∴S△ACD=6.
由此可得S四边形ABCD=2+6=8.
解法 2 由①知S△ABC=S△DAE=2,
由条件OD=3OB,得点D到AC的距离h 是点 B到AC的距离h 的3倍,则有S△ADC=3S△ABC=6, (等底模型)
从而可得四边形面积为8.
点评 本题综合较强,层层递进,主要考查了全等三角形的判定和性质,考查了等底模型.第(1)问关键在于作出公共高的辅助线 AH,构建等高模型.第(2)问注重了图形分析,并直接指出△ABC≌△DAE,这是解题的基本思想.第(3)问,①关键在于类比模仿第(2)问作答;②关键在于将四边形分成两个三角形,活用等底模型,或等高模型分析,体现了“借前结论攻后题”与“等积转换出妙招,巧在活用底与高”的战术思想.
例4如图18-10所示,在半径为5 的扇形 AOB中,∠AOB=90°,点 C,D 分别在半径OA 与 上,且AC=2,CD∥OB,点 P 是CD 上一动点,过 P 作OP 的垂线交AB=于点E,F,连接DE,DF.
(1) 求 的值.
(2) 如图18-11所示,连接EO,FO,若∠EOF=60°,求CP 的长.
(3)设CP=x,△DEF的面积为y,求y关于x的函数解析式,并写出自变量x的取值范围.
解析 (1) 作 DM⊥EF,垂足为M,如图18-12 所示.
∵OP⊥EF,∴PE=PF.
(2)∵∠EOF=60°,∴∠EOP=30°.
∵OC=AO-AC=3,
(3) 连接OD,如图18-13所示,在Rt△CDO中,OC=3,OD=5,
∴CD=4,PD=4-x.
作EH⊥CD,垂足为 H,
∵OC=3,CP=x,∴OP= +9.
在 Rt△EPO中,
∵∠COP+∠CPO=90°,∠EPH+∠CPO=90°,
∴∠COP=∠EPH.∴△OCP∽△PHE.
由此可得 则有 故
当点E与点A 重合时,EH=2,解得.
点评 本题涉及了圆弧、垂径定理、勾股定理、相似三角形的判定与性质、函数的解析式与自变量的取值范围等多个知识点,主要考查了等底的两个三角形面积比等于它们高的比的思想方法,考查了函数解析式的定义域的求解,综合性强.注重数形分析是解题关键所在.第(1)问,先挖掘OP 的长,再确定EF 的长是解题的基本思路.第(2)问,通过连接OE,结合∠EOF=60°,挖掘△EOF 为正三角形,再在Rt△EOP中,利用∠EOP 的余弦函数求得OP,进而求出 PC 是解题的常规思路.第(3)问,通过辅助线搭桥构建△OCP∽△PHE,利用相似比获得EH 的函数解析式是解题的必由之路.
跟踪训练
1. 如图所示,在△ABC中,DC的长度等于BD的2倍,DE 的长度等于AE 的长度.如果三角形ABC的面积是 20平方厘米,那么阴影部分的面积为 .
2. 如图所示,△ABC内的线段BD,CE相交于点O,已知OB=OD,OC=2OE,设△BOE,△COD,△BOC和四边形AEOD 的面积分别为S ,S ,S ,S .
(1) 求 S : S 的值.
(2) 如果 求S .
3. 如图所示,在 Rt△ACB中, 动点O从点C出发,沿着C→B→A→C的方向运动一周,以O为圆心,r为半径作圆.
(1) 若⊙O分别与AB,BC相切.
①利用直尺和圆规作⊙O(不写作法,保留作图痕迹).
②求出此时r的值.
(2)当r=1时,设⊙O在运动过程中与△ABC三条边的公共点个数为m,那么m的最小值是 ,最大值是
4. 如图1所示,在△ABC中,AB=AC,D为BC边上一点,DE⊥AB,垂足为E,DF⊥AC,垂足为 F.
作图:请作出AC边上的高BG.
探究:(1) 请你通过观察、测量找到 DE,DF,BG之间的数量关系:
(2)为了说明DE,DF,BG之间的数量关系,小嘉是这样做的:
连接AD,则有S△ADC= ,S△ABD = ,所以S△ABC=
S△ABC还可以表示为 .
………
请你帮小嘉完成上述填空.
拓展:如图2所示,当点D在如图2的位置时,上面DE,DF,BG之间的数量关系是否仍然成立 并说明理由.
对于前面所述的18种常用的初中平面几何辅助线,它们之间既有所不同,又相互关联.如“中点、中线想中位线,延线或作平行线”与“平行四边形,常连对角线”,等腰三角形中的“三线合一”与“垂线、角平分线,翻折集结等角与等线”等,它们只是出发点不同,思维方式不同,但所作的辅助线的图形却有可能是相同的.一般说来,平面几何辅助线十八招,也仅能给我们在探索解题途径时提供一个思考的方向和策略.但每一道题不是限用某一招术,每一招术也不是专用于某一类问题.解题实践表明,对同一平面几何问题,从不同的角度思考,所发掘的辅助线各有不同,从而得到的解法也有所不同.因此,对一些设计巧妙的几何题的求解,在运用这“18招”构建辅助线时,要把握命题的特点,善于猜想观察,大胆试探,勇于创新,不墨守成规,切合实际,兼而用之,切忌生搬硬套.通法歌诀综合用,创新解法乐无穷.只有这样,才能使我们全面理解解决问题的方法、掌握解决问题的程序,以此激活我们的思路,获取智慧和启迪.否则,我们的解题难以获得成效,数学思维也难以获得发展.
解题遇困难,千万莫慌张,
静心审条件,蛛丝马迹辨.
探究辅助线,请把歌诀念,
歌诀作指点,成功看得见.
例 如图1所示,在△ABC中,AB≠AC,点D,E在BC 边上,且 DE=EC,DF∥BA 交AE于点F,DF=AC,求证:AE平分∠BAC.
分析 题设条件简洁明了,但不够集中,需用辅助线开路架桥.若从“DE=EC”入手,当着眼于 E为DC 的中点时,想到“中点、中线想中位线,延线或作平行线”一招的辅助线.如图2所示,延长 FE 至点G,使 EG=FE,连接 CG,转证△DEF≌△CEG,得证法1.如图3所示,延长AE 至点G,使EG=AE,连接DG,转证△ACE≌△GDE,得证法2.当着眼于线段 DE与EC 共点且相等时,想到“边边相等又共点,常用旋转作试验”一招的辅助线,如图 2所示,将△DEF 绕点 E 旋转 180°,使点 D 与点C 重合,转证∠CAE=∠CGE,得证法3.若从“AE 平分∠BAC”入手,当着眼于“垂线、角平分线,翻折集结等角与等线”一招的辅助线时,如图5所示,作点 D 关于直线AE 的对称点P,连接EP,CP,DP,转证∠1=∠2,得证法4.当着眼于“三角形,若等腰,三线合一常用到”一招的辅助线时,过点 F 作FP∥AC,使FP=AC,连接CP,DP,设DP交AE 的延长线于点G,如图6所示,转证FG为等腰三角形FDP 底边上的中线,得证法5.如图7所示,延长AC至点Q,使AQ=AB,连接EQ,过点 F作FP∥AC交EQ 于点 P,连接 DP,CP,设DP交AE 的延长线于点G,转证 FG为等腰三角形 FDP 底边上的中线,得证法6.如图8所示,在AB上截取AM=AC,连接MC交AE于点N,转证 AN为等腰三角形AMC 底边上的中线,得证法7.
解析 证法1 延长 FE至点G,使得 EG=EF,连接CG,如图2所示,(中点中线中位线,延线或作平行线)
易证△DEF≌△CEG.
∴DF=CG,∠DFE=∠CGE.
∵DF=AC,
∴AC=CG,∠CAE=∠CGE.
又DF∥BA,∴∠BAE=∠DFE.
∴∠BAE=∠CAE.
故AE平分∠BAC.
证法2 延长AE 至点G,使EG=AE,连接DG,如图3所示.(中点、中线中位线,延线或作平行线)
在△ACE和△GDE中,
∴△ACE≌△GDE(SAS).
∴AC=GD,∠CAE=∠G.
∵DF=AC,∴DG=DF.
∴∠DFG=∠G.∴∠DFG=∠CAE.
∵DF∥AB,∴∠DFG=∠BAE.
∴∠BAE=∠CAE.
故AE平分∠BAC.
证法3 将△DEF绕点E 旋转 180°,使点 D 与点C 重合得△CEG,如图4所示.
(边边相等又共点,常用旋转作试验)
∴△DEF≌△CEG.
∴DF=CG,∠DFE=∠CGE.
由此可得F,E,G三点共线.
∵DF=AC,∴AC=CG.
∴∠CAE=∠CGE.
又DF∥BA,∴∠BAE=∠DFE.
所以∠BAE=∠CAE,即AE平分∠BAC.
证法4 如图5所示,过点 D作AE 的对称点 P,
连接EP,CP,DP,设DP交AE 的延长线于点G,
则 DG⊥AE,DF=FP.
从而可得DE=EP=EC,∠3=∠2.
(垂线、角平分线,翻折集结等角与等线)
∴△DPC是直角三角形,且∠CPD=90°,即CP⊥DP.
又DG⊥AE,∴CP∥AE.
过点C作CH⊥AE,垂足为 H,结合CP∥AE,得四边形CPGH 为矩形.
∴CH=PG,CP=HG.
又FP=FD=AC,∴Rt△ACH≌Rt△FPG.
∴AH=FG.∴AF=AH-FH=FG-FH=HG.
∴AF=HG=CP.又CP∥AE,
∴四边形 AFPC为平行四边形.
∴AC∥FP,从而可得∠1=∠2.
又DF∥AB,∴∠3=∠4.
∴∠1=∠4,即 AE平分∠BAC.
证法5 过点 F作 FP∥AC,使 FP=AC,连接CP,DP.
设DP 交AE 的延长线于点G,如图6所示,则四边形AFPC为平行四边形.
∴CP∥AE,∠1=∠2.
中小学教育资源及组卷应用平台
∵DE=EC,∴E为DC 的中点.
又EG∥CP,故G为DP 的中点.
故 FG为△DFP的边DP 上的中线.
(中点、中线想中位线,延线或作平行线)
又由已知得DF=AC=FP,
∴△DFP 为等腰三角形.
故 FG为等腰三角形DFP 顶角∠DFP 的平分线.
∴∠3=∠2.(三角形,若等腰,三线合一等底角)
又DF∥AB,∴∠3=∠4.
∴∠1=∠4,即AE平分∠BAC.
(遇见角角等倍分,移转割补找窍门)
证法6 如图7所示,∵AB>DF,DF=AC,∴AB>AC.
延长AC至点Q,使AQ=AB,连接EQ,过点 F作FP∥AC交EQ于点 P,
连接CP,DP,则有∠1=∠2.
又FD∥AB,由平行线分线段成比例,可得
∵AQ=AB,DF=AC,
∴DF=FP=AC.
结合FP∥AC,得四边形AFPC为平行四边形.
∴CP∥AE,且△DFP 为等腰三角形.
设DP 交AE 的延长线于点G,
∵DE=EC,∴E为DC 的中点.
又EG∥CP,故G为DP 的中点.
(中点、中线想中位线,延线或作平行线)
故 FG为△DFP 的边DP 上的中线.
故 FG为等腰三角形DFP 的顶角∠DFP 的平分线,∴∠3=∠2.
(三角形,若等腰,三线合一等底角)
又DF∥AB,∴∠3=∠4.
∴∠1=∠4,即AE平分∠BAC.
(遇见角角等倍分,移转割补找窍门)
证法7 依题意,显然有AB>AC.如图8所示.
在AB上截取AM=AC,连接MC,MD,
则△AMC为等腰三角形. ①
设MC交AE 于点N,
∵AM=AC=DF,DF∥AM,
∴四边形 AFDM 为平行四边形,故MD∥AE.
∵E为DC 的中点,∴N 为MC 的中点.
故 AN 为△AMC的边 MC 上的中线.②
由①②,得AN为等腰三角形AMC 的顶角∠MAC的平分线.(三线合一常用到)
由此可得AE平分∠BAC.
鉴于上述,本题主要考查了辅助线的添加方法,同时也考查了直角三角形、等腰三角形、角平分线以及全等三角形的判定与性质,考查了直观想象、逻辑推理等核心素养.命题涉及知识点多,综合性强,技巧性大.解题的关键在于如何添加辅助线,把分散的线段 DF,AC集中到某个三角形中去探究,所给出的7种证法各具特色.证法1与证法2思路相同,但辅助线不同(在同一证法中可以用到多条辅助线);证法3与证法1 辅助线相同,但思路不同(作法不同);证法4注重了对图形翻折的探究,体现了轴对称性的巧用;证法5、证法6、证法 7 都注重了“三线合一”思想方法的运用,凸显出了“遇见角角等倍分,移转割补找窍门”的解题策略,但所作的辅助线迥然有别.另外,证法2 的辅助线也可视为△AEC 绕点E 旋转180°而得.证法3的辅助线也可变为:过点C作CG∥DF交AE 的延长线于点G,等等.由此能使我们体会到:①辅助线画得好,解题轻松又快速.否则,解题必将绕弯或出错.②同一思路有不同的辅助线,同一辅助线有不同的思路.③从不同角度添加辅助线是实现一题多解的重要手段.
因此,我们想在平面几何思维新世界中不断发展、创新、前进,就务必要在平时的学习中,敢探索、勤思考、善归纳,这样才能不断长见识、增智慧、提能力.本书限于篇幅,只介绍了初中平面几何最常用的18种辅助线的添加方法.对于那些拔高或竞赛中所用的几何辅助线,如“梯形常把高凸显,时移腰或对角线”“两圆交,交点连,连心线垂公共弦”“两弦交,端点连,相似三角形呈现”等等,还需要读者在平面几何解题的实践中去体会、去探究、去发现.
答案
1. 8平方厘米 连接 DF,记点 C、点 F到AD边的距离分别为 dc,dF.
由等底等高的三角形的面积相等知,
故四边形AFDC的面积等于阴影部分面积的2倍.
则有 平方厘米).
故填8平方厘米.
2. (1) 记点 B到CE边的距离为h,
则有
故
(2)易知
根据(1)知
连接OA,设△AOE 的面积为S ,
则△AOD的面积为
由△AOD与△AOB等底等高,得 ①
又△AOE与△AOC等高, ②
由①②,得 故
3. (1)① 如图所示,作∠ABC的角平分线交AC于点O,以OC为半径作圆,则⊙O即为所求.
②∵∠C=90°,AC=1,BC=
即
(2)2,4 因为r=1,易知,动点O从点C 出发,沿着C→B→A→C的方向运动一周,有如下6种情形,如图2所示.
由图可得,m的最小值是 2,最大值是4,
故填2,4.
4. (1) BG=DE+DF.
由(1)可知,如图1所示.
S△ABC还可以表示为
【拓展】结论仍然成立,即BG=DE+DF.
连接AD,如图2所示.
∵DE⊥AB,DF⊥AC,AB=AC,
∴BG=DE+DF.
在题目给出的条件中,若当涉及三角形的面积或面积比时,往往离不开等积变换思想方法的运用.这是因为当三角形的高线一定时,它的底在底边所在直线上作任意移动,其面积不变,即等底共高的三角形面积相等.进而得到:等高的三角形的面积比等于其底的比;等底的三角形的面积比等于其高的比.由于三角形的任何一边都可以作为它的底.因此,三角形是等积变形中最活跃的图形.当把所研究的图形恰当地分解或组合成三角形,并根据题设的条件选定其底、高,巧用等积转换的思想方法来分析,往往可收到出奇制胜、事半功倍之效.此招辅助线我们可将它表述为:
等积转换出妙招,巧在活用底与高.
例1 在 Rt△ABC中,已知∠C=90°,AC=3,BC=4,以点C为圆心,r为半径作圆,要使圆与线段 AB有两个公共点,则r的值不可能是( ).
C. 3
解析 如图18-1所示,作CD⊥AB,垂足为D.(巧在活用底与高)
∵∠C=90°,AC=3,BC=4,
(等积转换出妙招)
即圆心C到AB的距离
因为AC
由此可得,要使⊙C与斜边AB 有两个公共点,则r的取值范围是
故选 D.
点评 此题考查了直线与圆的位置关系、直角三角形的性质,考查了等积转换思想的运用.解题关键是正确理解题意.这里先挖掘圆与线段AB有两个交点时r所在的范围,再由选项确定解是解题的基本思想.当然对本题的求解,亦可用排除法分析.如当r=3时有两个交点,当r>3时只能有一个交点,或没有交点.再结合选项即可得到解答.
例2如图18-2所示,已知扇形 AOB的半径OA=4,∠AOB=90°,点C,D分别在半径OA,OB上(点C不与点A重合),连接CD.点 P 是弧AB 上一点,PC=PD.
(1) 当 以 CD 为半径的⊙D 与⊙O 相切时,求 CD的长.
(2) 当点 D与点B 重合,点 P 为弧AB 的中点时,求∠OCD的度数.
(3) 如果OC=2,且四边形ODPC 是梯形,求 的值.
解析 (1) 如图18-2所示,由 可设OD=3k,OC=4k,则CD=5k.
由以CD为半径的⊙D 与⊙O相切,
得CD=DB=5k,OB=OA=8k.
∴AC=OC=4k=2.
(2) 如图18-3所示,连接OP,过点 P 作PE⊥OA,垂足为 E,PF⊥OB,垂足为 F.
∵PE⊥OA,PF⊥OB,∴PE=PF.
∵∠PEC=∠PFB=90°,PD=PC,
∴Rt△PEC≌Rt△PFB(HL).∴∠EPC=∠FPB.
∵∠PEO=∠EOF=∠OFP=90°,
∴∠EPF=90°.∴∠EPF=∠CPB=90°.
∴∠PCB=∠PBC=45°.
∵OP=OB,∠POB=45°,
∴∠OBP=∠OPB=67.5°.
(3)如图18-4所示,当OC∥PD时,
∵OC∥PD,∴∠PDO=∠AOD=90°.
过点C作CE⊥PD,垂足为 E,(巧在活用底与高)
∵CE⊥PD,∴∠CED=90°.
∴四边形OCED 是矩形.∴OC=DE=2,CE=OD.
设PC=PD=x,EC=OD=y,
则解得
如图18-5所示,当PC∥OD时,∵PC∥OD,∴∠COD=∠OCE=∠CED=90°.
过点 D作DE⊥PC,垂足为 E,(巧在活用底与高)
∴四边形OCED 是矩形.
∴OC=DE=2,CE=OD.
∵OP=4,OC=2,
综上所述 的值为 或
点评 本题综合性较强,涉及的知识点较多,主要考查了两圆的位置关系,解直角三角形,等腰三角形的性质,梯形的性质等知识,考查了分类讨论思想、等积转换思想.解题的关键是要正确地添加常用辅助线得到等高的三角形.属于中考压轴题.
例3 (1)探索发现 如图18-6 所示,在△ABC中,点 D 在边BC上,△ABD与△ADC 的面积分别记为S 与S ,试判断 的数量关系,并说明理由.
(2) 阅读分析 小东遇到这样一个问题:如图18-7 所示,在Rt△ABC中,AB=AC,∠BAC=90°,射线AM交 BC于点 D,点 E,F在AM上,且∠CEM=∠BFM=90°,试判断BF,CE,EF 三条线段之间的数量关系.
小东利用一对全等三角形,经过推理使问题得以解决.
填空:①在图18-7中的一对全等三角形为 与 .
② BF,CE,EF三条线段之间的数量关系为 .
(3)类比探究 如图18-8所示,在四边形ABCD中,AB=AD,AC与BD 交于点O,点E,F在射线AC 上,且∠BCF=∠DEF=∠BAD.
① 判断BC,DE,CE三条线段之间的数量关系,并说明理由.
② 若OD=3OB,△AED的面积为2,直接写出四边形 ABCD的面积.
解析 (1)结论:
理由:如图18-9所示,作AH⊥BC,垂足为 H.(巧在活用底与高)
(2) 如图18-7所示,
∵∠CEM=∠BFM=∠BAC=90°,
∴∠AEC=∠AFB=90°.
∴∠BAF+∠CAE=90°,∠CAE+∠ACE=90°,从而有∠BAF=∠ACE.
∵AB=AC,∴△AFB≌△CEA(AAS).
∴AF=CE,BF=AE.
∴CE=AF=AE+EF=BF+EF.
故答案为:①△AFB,△CEA.②CE=EF+BF.
(3)①在图18-8中,结论:DE=BC+CE.
理由:∵∠BCF=∠DEF,∴∠ACB=∠DEA.
∵∠BCF=∠BAD,∠BCF=∠ABC+∠BAC,∠BAD=∠BAC+∠DAE,
∴∠ABC=∠DAE.
∵AB=DA,∴△ABC≌△DAE(ASA).
∴BC=AE,AC=DE.
∵AC=AE+CE,∴DE=BC+CE.
②解法1 因为OD=3OB,
由(1)的结论得S△AOD=3S△ABO,S△ωD=3S△ωB,
∴S△ACD=3S△ABC.
∵△ABC≌△DEA,所以S△ABC=S△ADE=2.
∴S△ACD=6.
由此可得S四边形ABCD=2+6=8.
解法 2 由①知S△ABC=S△DAE=2,
由条件OD=3OB,得点D到AC的距离h 是点 B到AC的距离h 的3倍,则有S△ADC=3S△ABC=6, (等底模型)
从而可得四边形面积为8.
点评 本题综合较强,层层递进,主要考查了全等三角形的判定和性质,考查了等底模型.第(1)问关键在于作出公共高的辅助线 AH,构建等高模型.第(2)问注重了图形分析,并直接指出△ABC≌△DAE,这是解题的基本思想.第(3)问,①关键在于类比模仿第(2)问作答;②关键在于将四边形分成两个三角形,活用等底模型,或等高模型分析,体现了“借前结论攻后题”与“等积转换出妙招,巧在活用底与高”的战术思想.
例4如图18-10所示,在半径为5 的扇形 AOB中,∠AOB=90°,点 C,D 分别在半径OA 与 上,且AC=2,CD∥OB,点 P 是CD 上一动点,过 P 作OP 的垂线交AB=于点E,F,连接DE,DF.
(1) 求 的值.
(2) 如图18-11所示,连接EO,FO,若∠EOF=60°,求CP 的长.
(3)设CP=x,△DEF的面积为y,求y关于x的函数解析式,并写出自变量x的取值范围.
解析 (1) 作 DM⊥EF,垂足为M,如图18-12 所示.
∵OP⊥EF,∴PE=PF.
(2)∵∠EOF=60°,∴∠EOP=30°.
∵OC=AO-AC=3,
(3) 连接OD,如图18-13所示,在Rt△CDO中,OC=3,OD=5,
∴CD=4,PD=4-x.
作EH⊥CD,垂足为 H,
∵OC=3,CP=x,∴OP= +9.
在 Rt△EPO中,
∵∠COP+∠CPO=90°,∠EPH+∠CPO=90°,
∴∠COP=∠EPH.∴△OCP∽△PHE.
由此可得 则有 故
当点E与点A 重合时,EH=2,解得.
点评 本题涉及了圆弧、垂径定理、勾股定理、相似三角形的判定与性质、函数的解析式与自变量的取值范围等多个知识点,主要考查了等底的两个三角形面积比等于它们高的比的思想方法,考查了函数解析式的定义域的求解,综合性强.注重数形分析是解题关键所在.第(1)问,先挖掘OP 的长,再确定EF 的长是解题的基本思路.第(2)问,通过连接OE,结合∠EOF=60°,挖掘△EOF 为正三角形,再在Rt△EOP中,利用∠EOP 的余弦函数求得OP,进而求出 PC 是解题的常规思路.第(3)问,通过辅助线搭桥构建△OCP∽△PHE,利用相似比获得EH 的函数解析式是解题的必由之路.
跟踪训练
1. 如图所示,在△ABC中,DC的长度等于BD的2倍,DE 的长度等于AE 的长度.如果三角形ABC的面积是 20平方厘米,那么阴影部分的面积为 .
2. 如图所示,△ABC内的线段BD,CE相交于点O,已知OB=OD,OC=2OE,设△BOE,△COD,△BOC和四边形AEOD 的面积分别为S ,S ,S ,S .
(1) 求 S : S 的值.
(2) 如果 求S .
3. 如图所示,在 Rt△ACB中, 动点O从点C出发,沿着C→B→A→C的方向运动一周,以O为圆心,r为半径作圆.
(1) 若⊙O分别与AB,BC相切.
①利用直尺和圆规作⊙O(不写作法,保留作图痕迹).
②求出此时r的值.
(2)当r=1时,设⊙O在运动过程中与△ABC三条边的公共点个数为m,那么m的最小值是 ,最大值是
4. 如图1所示,在△ABC中,AB=AC,D为BC边上一点,DE⊥AB,垂足为E,DF⊥AC,垂足为 F.
作图:请作出AC边上的高BG.
探究:(1) 请你通过观察、测量找到 DE,DF,BG之间的数量关系:
(2)为了说明DE,DF,BG之间的数量关系,小嘉是这样做的:
连接AD,则有S△ADC= ,S△ABD = ,所以S△ABC=
S△ABC还可以表示为 .
………
请你帮小嘉完成上述填空.
拓展:如图2所示,当点D在如图2的位置时,上面DE,DF,BG之间的数量关系是否仍然成立 并说明理由.
对于前面所述的18种常用的初中平面几何辅助线,它们之间既有所不同,又相互关联.如“中点、中线想中位线,延线或作平行线”与“平行四边形,常连对角线”,等腰三角形中的“三线合一”与“垂线、角平分线,翻折集结等角与等线”等,它们只是出发点不同,思维方式不同,但所作的辅助线的图形却有可能是相同的.一般说来,平面几何辅助线十八招,也仅能给我们在探索解题途径时提供一个思考的方向和策略.但每一道题不是限用某一招术,每一招术也不是专用于某一类问题.解题实践表明,对同一平面几何问题,从不同的角度思考,所发掘的辅助线各有不同,从而得到的解法也有所不同.因此,对一些设计巧妙的几何题的求解,在运用这“18招”构建辅助线时,要把握命题的特点,善于猜想观察,大胆试探,勇于创新,不墨守成规,切合实际,兼而用之,切忌生搬硬套.通法歌诀综合用,创新解法乐无穷.只有这样,才能使我们全面理解解决问题的方法、掌握解决问题的程序,以此激活我们的思路,获取智慧和启迪.否则,我们的解题难以获得成效,数学思维也难以获得发展.
解题遇困难,千万莫慌张,
静心审条件,蛛丝马迹辨.
探究辅助线,请把歌诀念,
歌诀作指点,成功看得见.
例 如图1所示,在△ABC中,AB≠AC,点D,E在BC 边上,且 DE=EC,DF∥BA 交AE于点F,DF=AC,求证:AE平分∠BAC.
分析 题设条件简洁明了,但不够集中,需用辅助线开路架桥.若从“DE=EC”入手,当着眼于 E为DC 的中点时,想到“中点、中线想中位线,延线或作平行线”一招的辅助线.如图2所示,延长 FE 至点G,使 EG=FE,连接 CG,转证△DEF≌△CEG,得证法1.如图3所示,延长AE 至点G,使EG=AE,连接DG,转证△ACE≌△GDE,得证法2.当着眼于线段 DE与EC 共点且相等时,想到“边边相等又共点,常用旋转作试验”一招的辅助线,如图 2所示,将△DEF 绕点 E 旋转 180°,使点 D 与点C 重合,转证∠CAE=∠CGE,得证法3.若从“AE 平分∠BAC”入手,当着眼于“垂线、角平分线,翻折集结等角与等线”一招的辅助线时,如图5所示,作点 D 关于直线AE 的对称点P,连接EP,CP,DP,转证∠1=∠2,得证法4.当着眼于“三角形,若等腰,三线合一常用到”一招的辅助线时,过点 F 作FP∥AC,使FP=AC,连接CP,DP,设DP交AE 的延长线于点G,如图6所示,转证FG为等腰三角形FDP 底边上的中线,得证法5.如图7所示,延长AC至点Q,使AQ=AB,连接EQ,过点 F作FP∥AC交EQ 于点 P,连接 DP,CP,设DP交AE 的延长线于点G,转证 FG为等腰三角形 FDP 底边上的中线,得证法6.如图8所示,在AB上截取AM=AC,连接MC交AE于点N,转证 AN为等腰三角形AMC 底边上的中线,得证法7.
解析 证法1 延长 FE至点G,使得 EG=EF,连接CG,如图2所示,(中点中线中位线,延线或作平行线)
易证△DEF≌△CEG.
∴DF=CG,∠DFE=∠CGE.
∵DF=AC,
∴AC=CG,∠CAE=∠CGE.
又DF∥BA,∴∠BAE=∠DFE.
∴∠BAE=∠CAE.
故AE平分∠BAC.
证法2 延长AE 至点G,使EG=AE,连接DG,如图3所示.(中点、中线中位线,延线或作平行线)
在△ACE和△GDE中,
∴△ACE≌△GDE(SAS).
∴AC=GD,∠CAE=∠G.
∵DF=AC,∴DG=DF.
∴∠DFG=∠G.∴∠DFG=∠CAE.
∵DF∥AB,∴∠DFG=∠BAE.
∴∠BAE=∠CAE.
故AE平分∠BAC.
证法3 将△DEF绕点E 旋转 180°,使点 D 与点C 重合得△CEG,如图4所示.
(边边相等又共点,常用旋转作试验)
∴△DEF≌△CEG.
∴DF=CG,∠DFE=∠CGE.
由此可得F,E,G三点共线.
∵DF=AC,∴AC=CG.
∴∠CAE=∠CGE.
又DF∥BA,∴∠BAE=∠DFE.
所以∠BAE=∠CAE,即AE平分∠BAC.
证法4 如图5所示,过点 D作AE 的对称点 P,
连接EP,CP,DP,设DP交AE 的延长线于点G,
则 DG⊥AE,DF=FP.
从而可得DE=EP=EC,∠3=∠2.
(垂线、角平分线,翻折集结等角与等线)
∴△DPC是直角三角形,且∠CPD=90°,即CP⊥DP.
又DG⊥AE,∴CP∥AE.
过点C作CH⊥AE,垂足为 H,结合CP∥AE,得四边形CPGH 为矩形.
∴CH=PG,CP=HG.
又FP=FD=AC,∴Rt△ACH≌Rt△FPG.
∴AH=FG.∴AF=AH-FH=FG-FH=HG.
∴AF=HG=CP.又CP∥AE,
∴四边形 AFPC为平行四边形.
∴AC∥FP,从而可得∠1=∠2.
又DF∥AB,∴∠3=∠4.
∴∠1=∠4,即 AE平分∠BAC.
证法5 过点 F作 FP∥AC,使 FP=AC,连接CP,DP.
设DP 交AE 的延长线于点G,如图6所示,则四边形AFPC为平行四边形.
∴CP∥AE,∠1=∠2.
中小学教育资源及组卷应用平台
∵DE=EC,∴E为DC 的中点.
又EG∥CP,故G为DP 的中点.
故 FG为△DFP的边DP 上的中线.
(中点、中线想中位线,延线或作平行线)
又由已知得DF=AC=FP,
∴△DFP 为等腰三角形.
故 FG为等腰三角形DFP 顶角∠DFP 的平分线.
∴∠3=∠2.(三角形,若等腰,三线合一等底角)
又DF∥AB,∴∠3=∠4.
∴∠1=∠4,即AE平分∠BAC.
(遇见角角等倍分,移转割补找窍门)
证法6 如图7所示,∵AB>DF,DF=AC,∴AB>AC.
延长AC至点Q,使AQ=AB,连接EQ,过点 F作FP∥AC交EQ于点 P,
连接CP,DP,则有∠1=∠2.
又FD∥AB,由平行线分线段成比例,可得
∵AQ=AB,DF=AC,
∴DF=FP=AC.
结合FP∥AC,得四边形AFPC为平行四边形.
∴CP∥AE,且△DFP 为等腰三角形.
设DP 交AE 的延长线于点G,
∵DE=EC,∴E为DC 的中点.
又EG∥CP,故G为DP 的中点.
(中点、中线想中位线,延线或作平行线)
故 FG为△DFP 的边DP 上的中线.
故 FG为等腰三角形DFP 的顶角∠DFP 的平分线,∴∠3=∠2.
(三角形,若等腰,三线合一等底角)
又DF∥AB,∴∠3=∠4.
∴∠1=∠4,即AE平分∠BAC.
(遇见角角等倍分,移转割补找窍门)
证法7 依题意,显然有AB>AC.如图8所示.
在AB上截取AM=AC,连接MC,MD,
则△AMC为等腰三角形. ①
设MC交AE 于点N,
∵AM=AC=DF,DF∥AM,
∴四边形 AFDM 为平行四边形,故MD∥AE.
∵E为DC 的中点,∴N 为MC 的中点.
故 AN 为△AMC的边 MC 上的中线.②
由①②,得AN为等腰三角形AMC 的顶角∠MAC的平分线.(三线合一常用到)
由此可得AE平分∠BAC.
鉴于上述,本题主要考查了辅助线的添加方法,同时也考查了直角三角形、等腰三角形、角平分线以及全等三角形的判定与性质,考查了直观想象、逻辑推理等核心素养.命题涉及知识点多,综合性强,技巧性大.解题的关键在于如何添加辅助线,把分散的线段 DF,AC集中到某个三角形中去探究,所给出的7种证法各具特色.证法1与证法2思路相同,但辅助线不同(在同一证法中可以用到多条辅助线);证法3与证法1 辅助线相同,但思路不同(作法不同);证法4注重了对图形翻折的探究,体现了轴对称性的巧用;证法5、证法6、证法 7 都注重了“三线合一”思想方法的运用,凸显出了“遇见角角等倍分,移转割补找窍门”的解题策略,但所作的辅助线迥然有别.另外,证法2 的辅助线也可视为△AEC 绕点E 旋转180°而得.证法3的辅助线也可变为:过点C作CG∥DF交AE 的延长线于点G,等等.由此能使我们体会到:①辅助线画得好,解题轻松又快速.否则,解题必将绕弯或出错.②同一思路有不同的辅助线,同一辅助线有不同的思路.③从不同角度添加辅助线是实现一题多解的重要手段.
因此,我们想在平面几何思维新世界中不断发展、创新、前进,就务必要在平时的学习中,敢探索、勤思考、善归纳,这样才能不断长见识、增智慧、提能力.本书限于篇幅,只介绍了初中平面几何最常用的18种辅助线的添加方法.对于那些拔高或竞赛中所用的几何辅助线,如“梯形常把高凸显,时移腰或对角线”“两圆交,交点连,连心线垂公共弦”“两弦交,端点连,相似三角形呈现”等等,还需要读者在平面几何解题的实践中去体会、去探究、去发现.
答案
1. 8平方厘米 连接 DF,记点 C、点 F到AD边的距离分别为 dc,dF.
由等底等高的三角形的面积相等知,
故四边形AFDC的面积等于阴影部分面积的2倍.
则有 平方厘米).
故填8平方厘米.
2. (1) 记点 B到CE边的距离为h,
则有
故
(2)易知
根据(1)知
连接OA,设△AOE 的面积为S ,
则△AOD的面积为
由△AOD与△AOB等底等高,得 ①
又△AOE与△AOC等高, ②
由①②,得 故
3. (1)① 如图所示,作∠ABC的角平分线交AC于点O,以OC为半径作圆,则⊙O即为所求.
②∵∠C=90°,AC=1,BC=
即
(2)2,4 因为r=1,易知,动点O从点C 出发,沿着C→B→A→C的方向运动一周,有如下6种情形,如图2所示.
由图可得,m的最小值是 2,最大值是4,
故填2,4.
4. (1) BG=DE+DF.
由(1)可知,如图1所示.
S△ABC还可以表示为
【拓展】结论仍然成立,即BG=DE+DF.
连接AD,如图2所示.
∵DE⊥AB,DF⊥AC,AB=AC,
∴BG=DE+DF.
同课章节目录
