01.第一章 第一节 实数(含二次根式) 复习课件(28张PPT) 初中数学中考复习一轮复习
文档属性
| 名称 | 01.第一章 第一节 实数(含二次根式) 复习课件(28张PPT) 初中数学中考复习一轮复习 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-14 11:23:44 | ||
图片预览







文档简介
(共28张PPT)
第一章 数与式
第一节 实 数(含二次根式)
2025江西数学
精讲本
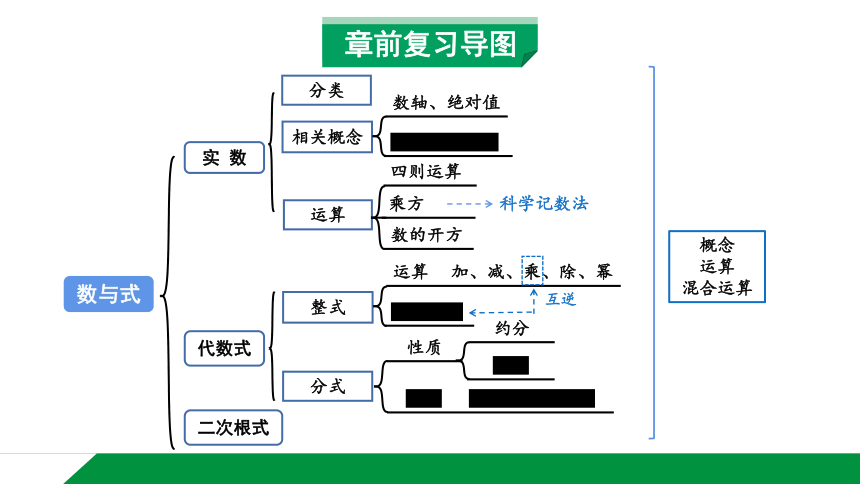
章前复习导图
数与式
相关概念
运算
分类
数的开方
四则运算
乘方
数轴、绝对值
相反数、倒数
科学记数法
整式
分式
运算 加、减、乘、除、幂
因式分解
性质
运算 加、减、乘、除
约分
通分
互逆
概念
运算
混合运算
实 数
代数式
二次根式
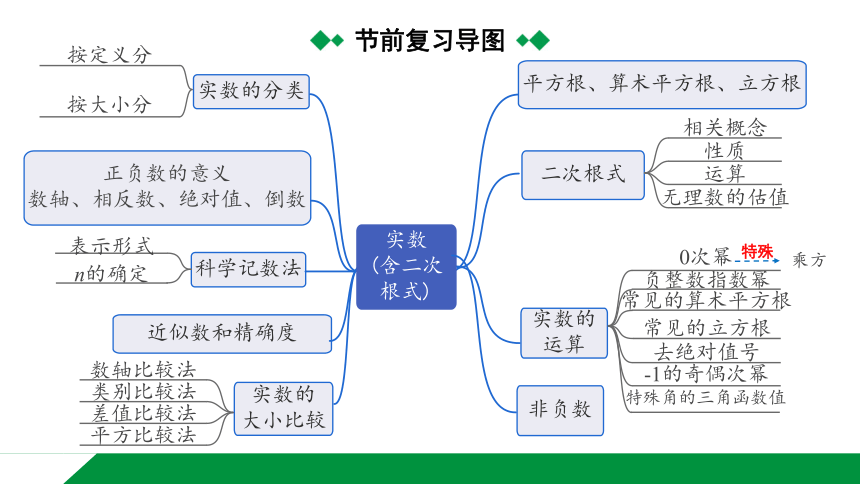
节前复习导图
实数的
运算
实数的分类
近似数和精确度
正负数的意义
数轴、相反数、绝对值、倒数
平方根、算术平方根、立方根
实数的
大小比较
实数
(含二次
根式)
二次根式
科学记数法
按定义分
按大小分
表示形式
n的确定
数轴比较法
类别比较法
差值比较法
平方比较法
相关概念
性质
运算
无理数的估值
负整数指数幂
去绝对值号
常见的算术平方根
常见的立方根
0次幂
-1的奇偶次幂
特殊角的三角函数值
非负数
乘方
特殊
温馨提示:点击内容可跳转至相应页面。
1
考点精讲
2
江西真题及变式
3
分层作业本
考点精讲
有理数 整数:正整数、0、负整数
分数:有限小数或________________
无理数:________________
实数
的分类
按定义分
【满分技法】初中阶段常见的4种无理数形式:
(1)开方开不尽的数,如、、等,注意、等是有理数;
(2)化简后含有根号的三角函数值,如sin 45°,sin 60°,cos 30°,
tan 30°,tan 60°等;
(3)有规律的无限不循环小数,如0.101 001 000…(相邻两个1之间依次多一个0);
(4)最终结果含π的数,如2π,等.
按大小分:正实数、0和_______,其中0既不是正数也不是负数,注:非负数包括正实数和0
无限循环小数
无限不循环小数
负实数
正负数的意义:正负数可以用于表示相反意义的量.如规定“盈(+)”,则“亏(-)”,“胜(+)”,则“负(-)”等
1. 三要素:
2. 实数与数轴上的点是一一对应的,数轴上两个点表示的数,右边的总比左边的大,正数大于0,负数小于0,正数大于负数
3. 如图,数轴上A、B两点之间的距离AB=________
数轴
1. 非零实数a的相反数为_______,特别地,0的相反数为0
2. 实数a,b互为相反数 a+b=________
3. 互为相反数的两个数表示的点分别位于数轴上原点的两侧(除0外),且到原点的距离_______,即互为相反数的两个数关于_________对称
相反数
原点
b-a
-a
0
相等
原点
________(a<0)
倒数
1.几何意义:数轴上表示这个点到原点的距离
2. |a| = ,
3. 离原点越远的数的________越大;绝对值相等的两个数相等或______________,|a|=|b| a=b或a=________
绝对值具有非负性(|a|≥0),即一个正数的绝对值是它________;负数的绝对值是它的________;0的绝对值是0
绝对值
1. 非零实数a的倒数是________.注意:______没有倒数,倒数等于它本身的数是_________
2. 实数a、b互为倒数 ab=_____
-a
本身
相反数
绝对值
互为相反数
-b
0
±1
1
a(a>0)
0(a=0)
科学记数 法
表示形式:a×10n,其中1≤|a|<10,n是整数
1. 当原数的绝对值≥10时,n为正整数,且等于原数的整数位数
减1或将原数变为a 时小数点向左移动的位数
2. 当0<原数的绝对值<1时,n为负整数,它的绝对值等于原数
左起第一个非零数字前所有零的个数(含小数点前的零)或原
数变为a时小数点向右移动的位数
n 的
确定
【满分技法】(1)常见的计数单位有:1万=______,1亿=______;常见的计
量单位有:1 mm=10-3 m,1 nm=______m;
(2)用科学记数法表示数时,要注意已知数据是否与表示数据单位一致.
104
108
10-9
近似数:将一个数四舍五入后得到的数
精确度:一般地,一个数四舍五入到哪一位,就说这个近似数精确
到哪一位.如:4.351精确到0.01为________
近似数
和精确度
数轴比较法:数轴上两个点表示的数,右边的点表示的数总比左边
的点表示的数________
类别比较法:正数>0>负数;两个负数比较大小,绝对值大的反
而小
差值比较法:a-b>0 a>b;a-b=0 a=b;a-b<0 a<b
平方比较法:a>(b≥0) a2________b(b≥0)
实数的
大小比较
4.35
大
>
考查点 定义 总结
平方根 实数a(a≥0)的平方根为_______,其中_____为a的算术平方根. 0的平方根为0 1.一个正数的平方根有两个,它们互为________
2.负数没有平方根
3.所有的数都只有一个立方根,且与原数同号
4.平方根等于它本身的数是0;算术平方根等于它本身的数是0,1;立方根等于它本身的数是_________
算术平 方根 立方根 实数a的立方根为________ 平方根、
算术平
方根、
立方根
±
相反数
0,±1
相关概念
性质
相关概念定义:形如(a≥0)的式子
有意义的条件:__________________________
1.被开方数不含________
2.被开方数不含___________的因数或因式
最简二次根式同时满足的两个条件
1.()2=______(a≥0)
a(a≥0)
______(a<0)
3.=· (a______0,b______0)
4.=(a______0,b______0)
5.双重非负性:a≥0,且≥0
2.=|a|=
二次
根式
>
被开方数大于等于0,即a≥0
分母
开得尽方
a
-a
≥
≥
≥
二次根式
加减法:一般地,二次根式加减时,可以先将各二次根式分别化成
_____________,再将被开方数________的二次根式进行合并
乘法: · =________(a≥0,b≥0)
除法: =________(a≥0,b>0)
运算
无理
数的
估值
1.先对二次根式平方
2.找出与平方后所得数字相邻的两个开得尽方的整数
3.对以上两个整数开方
4.确定这个根式的值在开方后所得的两个整数之间
最简二次根式
相同
实数的
运算
0次幂:a0=________(a≠0)
乘方:an=a·a·…·a,如(- )2=___,(-3)3=_____,(-)3=_____,
(-)3=_____
负整数指数幂:a-p=____(a≠0,p为正整数)(口诀:倒底数,反指数),特别
地,a-1=____,a-2=____.如(-)-1=____,(-)-2=___
常见的算术平方根:=________, =________, =________,
=________, =________, =______
常见的立方根:=________, =___________, =________,
=_______, =_______, =_________,
n个a
1
-27
-
-
-3
4
2
2
3
2
2
3
2
- 2
3
- 3
4
- 4
实数的
运算
________(a>b)
0(a=b)
________(a<b)
去绝对值符号:|a-b|=
a-b
b-a
【满分技法】先比较绝对值符号内两数的大小,再根据绝对值的非负性去绝对值符号.
________(n为偶数),如(-1)2 022=1
-1(n为奇数),如(-1)2 023=-1
sin 30°=,sin 45°=________, sin 60°=________,
cos 30°=,cos 45°= ,cos 60°= ,
tan 30°= ,tan 45°=1,tan 60°=________
-1的奇偶次幂:(-1)n =
1
特殊角的三
角函数值
1.常见的非负数有a2,|b|,(c≥0)
2.若几个非负数的和为0,则每个非负数的值均为0,如:若a2+|b|+=0,则有a2=0,|b|=0, =0,即a=b=c=________
非负数
0
命题点
1
实数的分类(10年2考)
1. (2023江西1题3分)下列各数中,正整数是 ( )
A. 3 B. 2.1 C. 0 D. -2
2. (2022江西1题3分)下列各数中,负数是( )
-1 B. 0 C. 2 D.
3. (2024江西样卷一)0.24不是( )
A. 分数 B. 小数 C. 有理数 D. 无理数
A
A
D
拓展训练
江西真题及变式
命题点
2
实数的相关概念(10年6考)
4. (2024江西1题3分)-5的相反数是( )
A. 5 B. -5 C. D. -
A
5. (2018江西1题3分)-2的绝对值是( )
A. -2 B. 2 C. - D.
6. (2020江西1题3分)-3的倒数是( )
3 B. -3 C. - D.
B
C
拓展训练
7. 如图,数轴上A,B两点在原点O的两侧,且OA=OB,若AB=4,那么点A表示的数是( )
4 B. -4
C. 2 D. -2
D
命题点
3
科学记数法(10年7考,数字均为大数)
8. (2024江西2题3分)“长征是宣言书,长征是宣传队,长征是播种机”.二万五千里长征是中国历史上的伟大壮举,也是人类史上的奇迹.将25 000用科学记数法可表示为( )
A. 0.25×106 B. 2.5×105 C. 2.5×104 D. 25×103
9. (2020江西3题3分)教育部近日发布了2019年全国教育经费执行情况统计快报,经初步统计,2019年全国教育经费总投入为50 175亿元,比上年增长8.74%,将50 175亿用科学记数法表示为( )
A. 5.017 5×1011 B. 5.017 5×1012 C. 0.501 75×1013 D. 0.501 75×1014
C
B
拓展训练
10. [跨语文学科](2024景德镇三模)“墙角数枝梅,凌寒独自开.遥知不是雪,为有暗香来.”出自宋代诗人王安石的《梅花》.梅花的花粉直径约为0.000 036 m,用科学记数法表示该数据为 .
11. (2024上海)科学家研发了一种新的蓝光唱片,一张蓝光唱片的容量约为2×105 GB,一张普通唱片的容量约为25 GB,则蓝光唱片的容量是普通唱片的 倍.(用科学记数法表示)
3.6×10-5
8×103
新考法
命题点
4
实数的大小比较(10年2考)
12. (2022江西2题3分)实数a,b在数轴上的对应点的位置如图所示,则下列结论中,正确的是( )
a>b B. a=b
C. a<b D. a=-b
13. (2024吉安三模改编)在实数,-,0,3中,最大的数是 ,最小的数是 ,比2大的无理数是 .
拓展训练
C
3
-
命题点
5
平方根、算术平方根、立方根(10年3考,均在实数的运算中
涉及考查)
14. (-8)2的平方根是 ,算术平方根是 ,立方根是 .
15. 一个正数的平方根分别是x+1和x-5,则x= .
基础小练
±8
8
4
2
16. (2023江西3题3分)若有意义,则a的值可以是( )
-1 B. 0 C. 2 D. 6
17. (2024江西样卷一)下列根式中,是最简二次根式的是( )
A. B. C. D.
拓展训练
二次根式(10年2考,仅2023年单独考查,2015年在整式的化简求值中涉及考查)
命题点
6
D
A
命题点
7
无理数的估值
基础小练
18. (北师八上复习题改编)估算的值在( )
A. 0和1之间 B. 1和2之间
C. 2和3之间 D. 3和4之间
19. (人教七下习题改编)已知x,y表示的整数部分和小数部分,则x-y的值为( )
A. -4 B. 4-
C. D. -2
C
B
命题点
8
实数的运算(10年11考,仅2018年未考查)
20. (2024江西7题3分)计算:(-1)2= .
21. (2017江西9题3分)中国人最先使用负数,魏晋时期的数学家刘徽在“正负术”的注文中指出,可将算筹(小棍形状的记数工具)正放表示正数,斜放表示负数.如图,根据刘徽的这种表示法,观察图①,可推算图②中所得的数值为 .
1
-3
22. [2024江西13(2)题3分]计算:π0+|-5|.
23. [2023江西(3)题3分]计算:+tan 45°-30.
24. [2022江西13(1)题3分]计算:|-2|+-20.
解:原式=1+5(2分)
=6.(3分)
解:原式=2+1-1(2分)
=2.(3分)
解:原式=2+2-1(2分)
=3.(3分)
25. [2021江西13(1)题3分]计算:(-1)2-(π-2 021)0+|-|.
26. [2020江西13(1)题3分]计算:(1-)0-|-2|+()-2.
解:原式=1-1+(2分)
=.(3分)
解:原式=1-2+22
=-1+4(2分)
=3.(3分)
请完成分层作业本第1~2页习题
第一章 数与式
第一节 实 数(含二次根式)
2025江西数学
精讲本
章前复习导图
数与式
相关概念
运算
分类
数的开方
四则运算
乘方
数轴、绝对值
相反数、倒数
科学记数法
整式
分式
运算 加、减、乘、除、幂
因式分解
性质
运算 加、减、乘、除
约分
通分
互逆
概念
运算
混合运算
实 数
代数式
二次根式
节前复习导图
实数的
运算
实数的分类
近似数和精确度
正负数的意义
数轴、相反数、绝对值、倒数
平方根、算术平方根、立方根
实数的
大小比较
实数
(含二次
根式)
二次根式
科学记数法
按定义分
按大小分
表示形式
n的确定
数轴比较法
类别比较法
差值比较法
平方比较法
相关概念
性质
运算
无理数的估值
负整数指数幂
去绝对值号
常见的算术平方根
常见的立方根
0次幂
-1的奇偶次幂
特殊角的三角函数值
非负数
乘方
特殊
温馨提示:点击内容可跳转至相应页面。
1
考点精讲
2
江西真题及变式
3
分层作业本
考点精讲
有理数 整数:正整数、0、负整数
分数:有限小数或________________
无理数:________________
实数
的分类
按定义分
【满分技法】初中阶段常见的4种无理数形式:
(1)开方开不尽的数,如、、等,注意、等是有理数;
(2)化简后含有根号的三角函数值,如sin 45°,sin 60°,cos 30°,
tan 30°,tan 60°等;
(3)有规律的无限不循环小数,如0.101 001 000…(相邻两个1之间依次多一个0);
(4)最终结果含π的数,如2π,等.
按大小分:正实数、0和_______,其中0既不是正数也不是负数,注:非负数包括正实数和0
无限循环小数
无限不循环小数
负实数
正负数的意义:正负数可以用于表示相反意义的量.如规定“盈(+)”,则“亏(-)”,“胜(+)”,则“负(-)”等
1. 三要素:
2. 实数与数轴上的点是一一对应的,数轴上两个点表示的数,右边的总比左边的大,正数大于0,负数小于0,正数大于负数
3. 如图,数轴上A、B两点之间的距离AB=________
数轴
1. 非零实数a的相反数为_______,特别地,0的相反数为0
2. 实数a,b互为相反数 a+b=________
3. 互为相反数的两个数表示的点分别位于数轴上原点的两侧(除0外),且到原点的距离_______,即互为相反数的两个数关于_________对称
相反数
原点
b-a
-a
0
相等
原点
________(a<0)
倒数
1.几何意义:数轴上表示这个点到原点的距离
2. |a| = ,
3. 离原点越远的数的________越大;绝对值相等的两个数相等或______________,|a|=|b| a=b或a=________
绝对值具有非负性(|a|≥0),即一个正数的绝对值是它________;负数的绝对值是它的________;0的绝对值是0
绝对值
1. 非零实数a的倒数是________.注意:______没有倒数,倒数等于它本身的数是_________
2. 实数a、b互为倒数 ab=_____
-a
本身
相反数
绝对值
互为相反数
-b
0
±1
1
a(a>0)
0(a=0)
科学记数 法
表示形式:a×10n,其中1≤|a|<10,n是整数
1. 当原数的绝对值≥10时,n为正整数,且等于原数的整数位数
减1或将原数变为a 时小数点向左移动的位数
2. 当0<原数的绝对值<1时,n为负整数,它的绝对值等于原数
左起第一个非零数字前所有零的个数(含小数点前的零)或原
数变为a时小数点向右移动的位数
n 的
确定
【满分技法】(1)常见的计数单位有:1万=______,1亿=______;常见的计
量单位有:1 mm=10-3 m,1 nm=______m;
(2)用科学记数法表示数时,要注意已知数据是否与表示数据单位一致.
104
108
10-9
近似数:将一个数四舍五入后得到的数
精确度:一般地,一个数四舍五入到哪一位,就说这个近似数精确
到哪一位.如:4.351精确到0.01为________
近似数
和精确度
数轴比较法:数轴上两个点表示的数,右边的点表示的数总比左边
的点表示的数________
类别比较法:正数>0>负数;两个负数比较大小,绝对值大的反
而小
差值比较法:a-b>0 a>b;a-b=0 a=b;a-b<0 a<b
平方比较法:a>(b≥0) a2________b(b≥0)
实数的
大小比较
4.35
大
>
考查点 定义 总结
平方根 实数a(a≥0)的平方根为_______,其中_____为a的算术平方根. 0的平方根为0 1.一个正数的平方根有两个,它们互为________
2.负数没有平方根
3.所有的数都只有一个立方根,且与原数同号
4.平方根等于它本身的数是0;算术平方根等于它本身的数是0,1;立方根等于它本身的数是_________
算术平 方根 立方根 实数a的立方根为________ 平方根、
算术平
方根、
立方根
±
相反数
0,±1
相关概念
性质
相关概念定义:形如(a≥0)的式子
有意义的条件:__________________________
1.被开方数不含________
2.被开方数不含___________的因数或因式
最简二次根式同时满足的两个条件
1.()2=______(a≥0)
a(a≥0)
______(a<0)
3.=· (a______0,b______0)
4.=(a______0,b______0)
5.双重非负性:a≥0,且≥0
2.=|a|=
二次
根式
>
被开方数大于等于0,即a≥0
分母
开得尽方
a
-a
≥
≥
≥
二次根式
加减法:一般地,二次根式加减时,可以先将各二次根式分别化成
_____________,再将被开方数________的二次根式进行合并
乘法: · =________(a≥0,b≥0)
除法: =________(a≥0,b>0)
运算
无理
数的
估值
1.先对二次根式平方
2.找出与平方后所得数字相邻的两个开得尽方的整数
3.对以上两个整数开方
4.确定这个根式的值在开方后所得的两个整数之间
最简二次根式
相同
实数的
运算
0次幂:a0=________(a≠0)
乘方:an=a·a·…·a,如(- )2=___,(-3)3=_____,(-)3=_____,
(-)3=_____
负整数指数幂:a-p=____(a≠0,p为正整数)(口诀:倒底数,反指数),特别
地,a-1=____,a-2=____.如(-)-1=____,(-)-2=___
常见的算术平方根:=________, =________, =________,
=________, =________, =______
常见的立方根:=________, =___________, =________,
=_______, =_______, =_________,
n个a
1
-27
-
-
-3
4
2
2
3
2
2
3
2
- 2
3
- 3
4
- 4
实数的
运算
________(a>b)
0(a=b)
________(a<b)
去绝对值符号:|a-b|=
a-b
b-a
【满分技法】先比较绝对值符号内两数的大小,再根据绝对值的非负性去绝对值符号.
________(n为偶数),如(-1)2 022=1
-1(n为奇数),如(-1)2 023=-1
sin 30°=,sin 45°=________, sin 60°=________,
cos 30°=,cos 45°= ,cos 60°= ,
tan 30°= ,tan 45°=1,tan 60°=________
-1的奇偶次幂:(-1)n =
1
特殊角的三
角函数值
1.常见的非负数有a2,|b|,(c≥0)
2.若几个非负数的和为0,则每个非负数的值均为0,如:若a2+|b|+=0,则有a2=0,|b|=0, =0,即a=b=c=________
非负数
0
命题点
1
实数的分类(10年2考)
1. (2023江西1题3分)下列各数中,正整数是 ( )
A. 3 B. 2.1 C. 0 D. -2
2. (2022江西1题3分)下列各数中,负数是( )
-1 B. 0 C. 2 D.
3. (2024江西样卷一)0.24不是( )
A. 分数 B. 小数 C. 有理数 D. 无理数
A
A
D
拓展训练
江西真题及变式
命题点
2
实数的相关概念(10年6考)
4. (2024江西1题3分)-5的相反数是( )
A. 5 B. -5 C. D. -
A
5. (2018江西1题3分)-2的绝对值是( )
A. -2 B. 2 C. - D.
6. (2020江西1题3分)-3的倒数是( )
3 B. -3 C. - D.
B
C
拓展训练
7. 如图,数轴上A,B两点在原点O的两侧,且OA=OB,若AB=4,那么点A表示的数是( )
4 B. -4
C. 2 D. -2
D
命题点
3
科学记数法(10年7考,数字均为大数)
8. (2024江西2题3分)“长征是宣言书,长征是宣传队,长征是播种机”.二万五千里长征是中国历史上的伟大壮举,也是人类史上的奇迹.将25 000用科学记数法可表示为( )
A. 0.25×106 B. 2.5×105 C. 2.5×104 D. 25×103
9. (2020江西3题3分)教育部近日发布了2019年全国教育经费执行情况统计快报,经初步统计,2019年全国教育经费总投入为50 175亿元,比上年增长8.74%,将50 175亿用科学记数法表示为( )
A. 5.017 5×1011 B. 5.017 5×1012 C. 0.501 75×1013 D. 0.501 75×1014
C
B
拓展训练
10. [跨语文学科](2024景德镇三模)“墙角数枝梅,凌寒独自开.遥知不是雪,为有暗香来.”出自宋代诗人王安石的《梅花》.梅花的花粉直径约为0.000 036 m,用科学记数法表示该数据为 .
11. (2024上海)科学家研发了一种新的蓝光唱片,一张蓝光唱片的容量约为2×105 GB,一张普通唱片的容量约为25 GB,则蓝光唱片的容量是普通唱片的 倍.(用科学记数法表示)
3.6×10-5
8×103
新考法
命题点
4
实数的大小比较(10年2考)
12. (2022江西2题3分)实数a,b在数轴上的对应点的位置如图所示,则下列结论中,正确的是( )
a>b B. a=b
C. a<b D. a=-b
13. (2024吉安三模改编)在实数,-,0,3中,最大的数是 ,最小的数是 ,比2大的无理数是 .
拓展训练
C
3
-
命题点
5
平方根、算术平方根、立方根(10年3考,均在实数的运算中
涉及考查)
14. (-8)2的平方根是 ,算术平方根是 ,立方根是 .
15. 一个正数的平方根分别是x+1和x-5,则x= .
基础小练
±8
8
4
2
16. (2023江西3题3分)若有意义,则a的值可以是( )
-1 B. 0 C. 2 D. 6
17. (2024江西样卷一)下列根式中,是最简二次根式的是( )
A. B. C. D.
拓展训练
二次根式(10年2考,仅2023年单独考查,2015年在整式的化简求值中涉及考查)
命题点
6
D
A
命题点
7
无理数的估值
基础小练
18. (北师八上复习题改编)估算的值在( )
A. 0和1之间 B. 1和2之间
C. 2和3之间 D. 3和4之间
19. (人教七下习题改编)已知x,y表示的整数部分和小数部分,则x-y的值为( )
A. -4 B. 4-
C. D. -2
C
B
命题点
8
实数的运算(10年11考,仅2018年未考查)
20. (2024江西7题3分)计算:(-1)2= .
21. (2017江西9题3分)中国人最先使用负数,魏晋时期的数学家刘徽在“正负术”的注文中指出,可将算筹(小棍形状的记数工具)正放表示正数,斜放表示负数.如图,根据刘徽的这种表示法,观察图①,可推算图②中所得的数值为 .
1
-3
22. [2024江西13(2)题3分]计算:π0+|-5|.
23. [2023江西(3)题3分]计算:+tan 45°-30.
24. [2022江西13(1)题3分]计算:|-2|+-20.
解:原式=1+5(2分)
=6.(3分)
解:原式=2+1-1(2分)
=2.(3分)
解:原式=2+2-1(2分)
=3.(3分)
25. [2021江西13(1)题3分]计算:(-1)2-(π-2 021)0+|-|.
26. [2020江西13(1)题3分]计算:(1-)0-|-2|+()-2.
解:原式=1-1+(2分)
=.(3分)
解:原式=1-2+22
=-1+4(2分)
=3.(3分)
请完成分层作业本第1~2页习题
同课章节目录
