2024-2025学年八年级数学人教版上册寒假作业(综合复习能力提升篇)(含答案)
文档属性
| 名称 | 2024-2025学年八年级数学人教版上册寒假作业(综合复习能力提升篇)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 917.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-14 00:00:00 | ||
图片预览




文档简介
2024-2025学年八年级数学人教版上册
寒假作业(综合复习能力提升篇)
一、选择题
1.从六边形的一个顶点出发,可以画出m条对角线,它们将六边形分成n个三角形.则的值为 ( )
A.0 B.1 C.6 D.
2.如图,是中的平分线,是的外角的平分线,如果,,则( )
A. B. C. D.
3.下列从左边到右边的变形,是因式分解的是( )
A. B.
C. D.
4.若,则( )
A.3 B.6 C. D.
5.如图,在和中,点、、在同一直线上,已知,,添加以下条件后,仍不能判定的是( )
A. B.
C. D.
6.如图,已知的周长是30,,分别平分、,于点D,且,则的面积为( )
A.30 B.35 C.40 D.45
7.如图,将一张长方形纸片分别沿着,折叠,使边,均落在上,得到折痕,,则等于( )
A.30° B.35° C.45° D.60°
8.如图,在中,,平分,于D.如果,,那么
A. B. C. D.
9.《九章算术》中有一道关于古代驿站送信的题目,其白话译文为:一份文件,若用慢马送到里远的城市,所需时间比规定时间多天;若改为快马派送,则所需时间比规定时间少天,已知快马的速度是慢马的倍,求规定时间,设规定时间为天,则可列出正确的方程为( )
A. B.
C. D.
10.如图,在锐角中,是边上的高.,且,连接,交的延长线于点,连接,下列结论:;;;是中点.其中一定正确的个数是( )
A.个 B.个 C.个 D.个
二、填空题
11.已知:,则的值为 .
12.已知关于x的方程有增根,那么 .
13.如图,在中,延长至点,使得,延长至点,使得,延长至点,使得,连接、、,若,则为 .
14.如图,,,,如果点P在线段上以/秒的速度由B点向C点运动,同时,点Q从C点出发沿射线运动,若经过t秒后,与全等,则t的值是 .
15.如图,在长方形中,点E在上,且,分别以,为折痕进行折叠并压平,若,则 .
16.已知有理数满足,那么的值为 .
三、解答题
17.先化简,再求值:,其中.
18.分解因式:
(1); (2).
19.(1)解分式方程: (2)解分式方程:
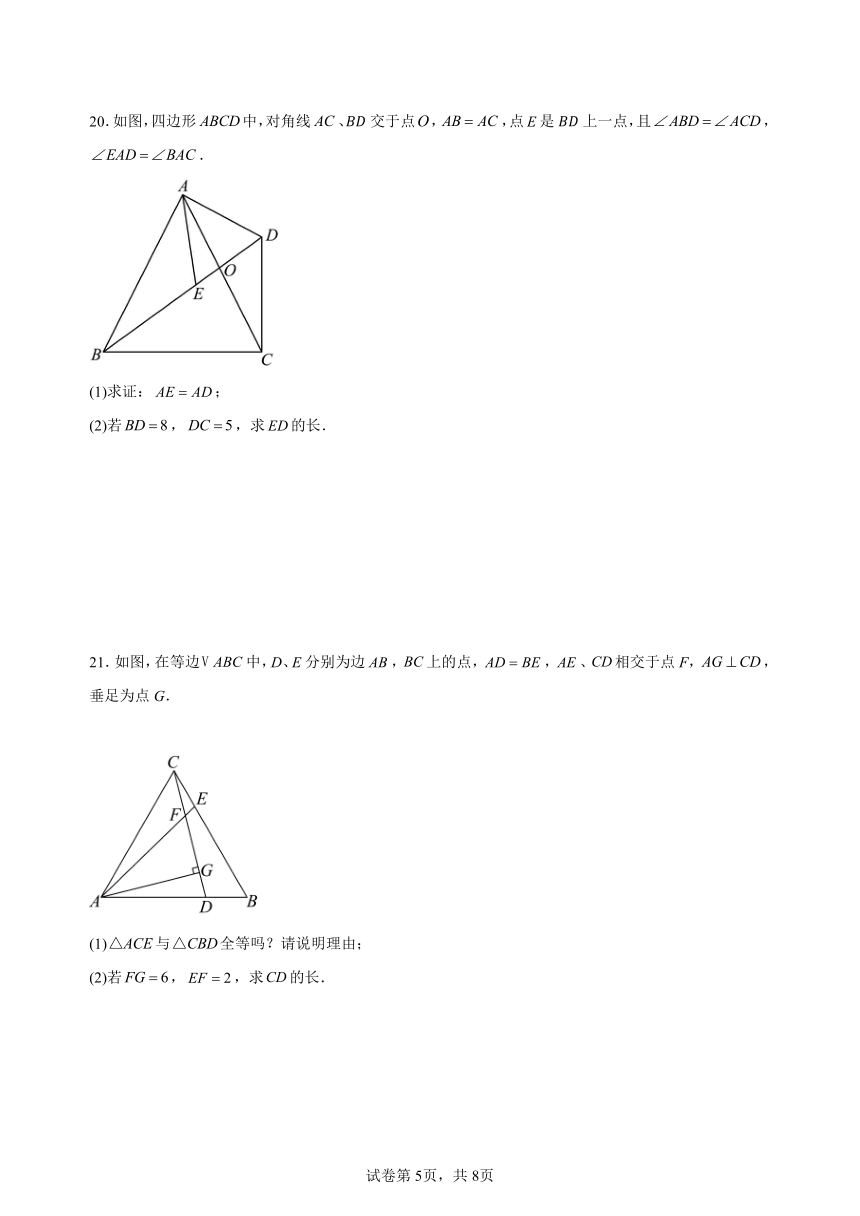
20.如图,四边形中,对角线、交于点,,点是上一点,且,.
(1)求证:;
(2)若,,求的长.
21.如图,在等边中,D、E分别为边,上的点,,、相交于点F,,垂足为点G.
(1)与全等吗?请说明理由;
(2)若,,求的长.
22.已知的三边长是,,。
(1)若,,且三角形的周长是小于16的偶数,求的值;
(2)化简.
23.拓广探索:
若x满足,求的值.
解:设,
则,
∴.
请仿照上面的方法求解问题:
(1)若x满足,求的值.
(2)已知正方形的边长为分别是、上的点,且,,长方形的面积是,分别以、为边作正方形,求阴影部分的面积.
24.我们定义:在一个三角形中,若一个角的度数是另一个角度数的倍,则这样的三角形称之为“和谐三角形”如:三个内角分别为,,的三角形是“和谐三角形”.
【概念理解】
如图,,点在边上,过点作交于点,以为端点作射线,交线段于点(点不与,重合)
(1)的度数为 , (填“是”或“不是”)“和谐三角形”;
(2)若,试说明:是“和谐三角形”.
【应用拓展】
(3)如图,点在的边上,连结,作的平分线交于点,在上取点,使,若是“和谐三角形”,请直接写出的度数.
25.已知,中,,,一直线过顶点,过,分别作其垂线,垂足分别为,.
(1)如图1,求证:;
(2)如图2,当直线穿过的内部且时,请探索线段,,之间的数量关系,并说明理由;
(3)在(2)的条件下,若,,求的面积.
26.小郝同学在当建造师的爸爸的一份资料上看到一段文字:“民用住宅窗户面积应小于地板面积,但窗户面积与地板面积的比值越大,住宅的采光条件会越好.”
小郝思考:如果同时增加相等的窗户面积和地板面积,住宅的采光条件会不会更好?为了验证这猜想,小郝做了如下数学实验:
第一步:假设某住宅窗户面积为17平方米,地板面积为80平方米,则.如果窗户面积和地板面积同时增加1平方米,则,此时:
∵,
∴,
所以,同时增加相等的窗户面积和地板面积,住宅的采光条件会更好.
第二步:假设某住宅窗户面积为x平方米,地板面积为y平方米,且y>x>0,则,如果窗户面积和地板面积同时增加1平方米,则.
请帮小郝完成猜想证明过程.
第三步:假设某住宅窗户面积为x平方米,地板面积为y平方米,且y>x>0,则.如果窗户面积和地板面积同时增加m平方米,则.
请帮小郝完成猜想证明过程,井对问题下结论.
试卷第1页,共3页
试卷第1页,共3页
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B C B B D D C B B A
11.
12.1
13.
14.1或
15./度
16.
17.,
18.
【小题1】解:原式;
【小题2】解:原式.
19.解:(1)
检验,当,,即是增根,
∴分式方程无解.
(2)
两边同时乘
检验,当时,
∴
20.(1)证明:,
,
即:,
在和中,
,
∴,
;
(2)解:由(1)得,
,
,,
.
21.(1)解:与全等,理由如下:
是等边三角形,
,
,
,即,
在和中,
,
;
(2)解:,
,,
,
,
,
,
,
,
,
.
22.(1)解:的三边长是,,,
,即,
三角形的周长是小于16的偶数,
即,
;
(2)解:由三角形三边关系得:,
,,
.
23.(1)解:设,,
则,,
∴;
(2)∵正方形的边长为,,
∴,,
设,,
则,,
∴,
∴,
∴,
∴阴影部分的面积为.
24.解:()∵,
∴,
∴,
∴,
∴不是“和谐三角形”;
故答案为:, 不是;
()∵是的一个外角,
∴,
又∵,,
∴,,
∴,
∴是“和谐三角形”;
()∵,,
∴,
∴,
∴,
∵,
∴,
∵,
∴,
∵平分,
∴,
∴,
∵是“和谐三角形”,
∴或,
∵,
∴或.
25.(1)证明:,
,
又,,
,
,
,
在和中,
,
,
,,
,
;
(2)解:,理由如下:
,,
,
又,
,
,,
,
即;
(3)解:由(2)得,,,
又,
,
,
,
,,
的面积.
26.证明:第二步:
即
∴窗户面积和地板面积同时增加1平方米,住宅的采光条件会更好;
第三步:同理可得,
∵y>x>0,m>0,
∴y-x>0,m(y-x)>0,y(y+m)>0,
,
,
∴窗户面积和地板面积同时增加m平方米,住宅的采光条件会更好;
结论:同时增加相等的窗户面积和地板面积,住宅的采光条件会更好.
答案第1页,共2页
答案第1页,共2页
寒假作业(综合复习能力提升篇)
一、选择题
1.从六边形的一个顶点出发,可以画出m条对角线,它们将六边形分成n个三角形.则的值为 ( )
A.0 B.1 C.6 D.
2.如图,是中的平分线,是的外角的平分线,如果,,则( )
A. B. C. D.
3.下列从左边到右边的变形,是因式分解的是( )
A. B.
C. D.
4.若,则( )
A.3 B.6 C. D.
5.如图,在和中,点、、在同一直线上,已知,,添加以下条件后,仍不能判定的是( )
A. B.
C. D.
6.如图,已知的周长是30,,分别平分、,于点D,且,则的面积为( )
A.30 B.35 C.40 D.45
7.如图,将一张长方形纸片分别沿着,折叠,使边,均落在上,得到折痕,,则等于( )
A.30° B.35° C.45° D.60°
8.如图,在中,,平分,于D.如果,,那么
A. B. C. D.
9.《九章算术》中有一道关于古代驿站送信的题目,其白话译文为:一份文件,若用慢马送到里远的城市,所需时间比规定时间多天;若改为快马派送,则所需时间比规定时间少天,已知快马的速度是慢马的倍,求规定时间,设规定时间为天,则可列出正确的方程为( )
A. B.
C. D.
10.如图,在锐角中,是边上的高.,且,连接,交的延长线于点,连接,下列结论:;;;是中点.其中一定正确的个数是( )
A.个 B.个 C.个 D.个
二、填空题
11.已知:,则的值为 .
12.已知关于x的方程有增根,那么 .
13.如图,在中,延长至点,使得,延长至点,使得,延长至点,使得,连接、、,若,则为 .
14.如图,,,,如果点P在线段上以/秒的速度由B点向C点运动,同时,点Q从C点出发沿射线运动,若经过t秒后,与全等,则t的值是 .
15.如图,在长方形中,点E在上,且,分别以,为折痕进行折叠并压平,若,则 .
16.已知有理数满足,那么的值为 .
三、解答题
17.先化简,再求值:,其中.
18.分解因式:
(1); (2).
19.(1)解分式方程: (2)解分式方程:
20.如图,四边形中,对角线、交于点,,点是上一点,且,.
(1)求证:;
(2)若,,求的长.
21.如图,在等边中,D、E分别为边,上的点,,、相交于点F,,垂足为点G.
(1)与全等吗?请说明理由;
(2)若,,求的长.
22.已知的三边长是,,。
(1)若,,且三角形的周长是小于16的偶数,求的值;
(2)化简.
23.拓广探索:
若x满足,求的值.
解:设,
则,
∴.
请仿照上面的方法求解问题:
(1)若x满足,求的值.
(2)已知正方形的边长为分别是、上的点,且,,长方形的面积是,分别以、为边作正方形,求阴影部分的面积.
24.我们定义:在一个三角形中,若一个角的度数是另一个角度数的倍,则这样的三角形称之为“和谐三角形”如:三个内角分别为,,的三角形是“和谐三角形”.
【概念理解】
如图,,点在边上,过点作交于点,以为端点作射线,交线段于点(点不与,重合)
(1)的度数为 , (填“是”或“不是”)“和谐三角形”;
(2)若,试说明:是“和谐三角形”.
【应用拓展】
(3)如图,点在的边上,连结,作的平分线交于点,在上取点,使,若是“和谐三角形”,请直接写出的度数.
25.已知,中,,,一直线过顶点,过,分别作其垂线,垂足分别为,.
(1)如图1,求证:;
(2)如图2,当直线穿过的内部且时,请探索线段,,之间的数量关系,并说明理由;
(3)在(2)的条件下,若,,求的面积.
26.小郝同学在当建造师的爸爸的一份资料上看到一段文字:“民用住宅窗户面积应小于地板面积,但窗户面积与地板面积的比值越大,住宅的采光条件会越好.”
小郝思考:如果同时增加相等的窗户面积和地板面积,住宅的采光条件会不会更好?为了验证这猜想,小郝做了如下数学实验:
第一步:假设某住宅窗户面积为17平方米,地板面积为80平方米,则.如果窗户面积和地板面积同时增加1平方米,则,此时:
∵,
∴,
所以,同时增加相等的窗户面积和地板面积,住宅的采光条件会更好.
第二步:假设某住宅窗户面积为x平方米,地板面积为y平方米,且y>x>0,则,如果窗户面积和地板面积同时增加1平方米,则.
请帮小郝完成猜想证明过程.
第三步:假设某住宅窗户面积为x平方米,地板面积为y平方米,且y>x>0,则.如果窗户面积和地板面积同时增加m平方米,则.
请帮小郝完成猜想证明过程,井对问题下结论.
试卷第1页,共3页
试卷第1页,共3页
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B C B B D D C B B A
11.
12.1
13.
14.1或
15./度
16.
17.,
18.
【小题1】解:原式;
【小题2】解:原式.
19.解:(1)
检验,当,,即是增根,
∴分式方程无解.
(2)
两边同时乘
检验,当时,
∴
20.(1)证明:,
,
即:,
在和中,
,
∴,
;
(2)解:由(1)得,
,
,,
.
21.(1)解:与全等,理由如下:
是等边三角形,
,
,
,即,
在和中,
,
;
(2)解:,
,,
,
,
,
,
,
,
,
.
22.(1)解:的三边长是,,,
,即,
三角形的周长是小于16的偶数,
即,
;
(2)解:由三角形三边关系得:,
,,
.
23.(1)解:设,,
则,,
∴;
(2)∵正方形的边长为,,
∴,,
设,,
则,,
∴,
∴,
∴,
∴阴影部分的面积为.
24.解:()∵,
∴,
∴,
∴,
∴不是“和谐三角形”;
故答案为:, 不是;
()∵是的一个外角,
∴,
又∵,,
∴,,
∴,
∴是“和谐三角形”;
()∵,,
∴,
∴,
∴,
∵,
∴,
∵,
∴,
∵平分,
∴,
∴,
∵是“和谐三角形”,
∴或,
∵,
∴或.
25.(1)证明:,
,
又,,
,
,
,
在和中,
,
,
,,
,
;
(2)解:,理由如下:
,,
,
又,
,
,,
,
即;
(3)解:由(2)得,,,
又,
,
,
,
,,
的面积.
26.证明:第二步:
即
∴窗户面积和地板面积同时增加1平方米,住宅的采光条件会更好;
第三步:同理可得,
∵y>x>0,m>0,
∴y-x>0,m(y-x)>0,y(y+m)>0,
,
,
∴窗户面积和地板面积同时增加m平方米,住宅的采光条件会更好;
结论:同时增加相等的窗户面积和地板面积,住宅的采光条件会更好.
答案第1页,共2页
答案第1页,共2页
同课章节目录
