3.1.1 椭圆的标准方程 课件(共20张PPT) 湘教版(2020)高中数学选择性必修第一册
文档属性
| 名称 | 3.1.1 椭圆的标准方程 课件(共20张PPT) 湘教版(2020)高中数学选择性必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-14 07:44:47 | ||
图片预览







文档简介
(共20张PPT)
第三章 圆锥曲线与方程
3.1 椭 圆
3.1.1 椭圆的标准方程
1.了解椭圆的实际背景,感受椭圆在刻画现实世界和解决实际问题中的作用.(重点)
2.掌握椭圆的定义,会求椭圆的标准方程.(重点、难点)
通过图片我们看到,在我们所生活的世界中,随处可见椭圆这种图形,而且我们也已经知道了椭圆的大致形状,那么我们能否动手画一个标准的椭圆呢?
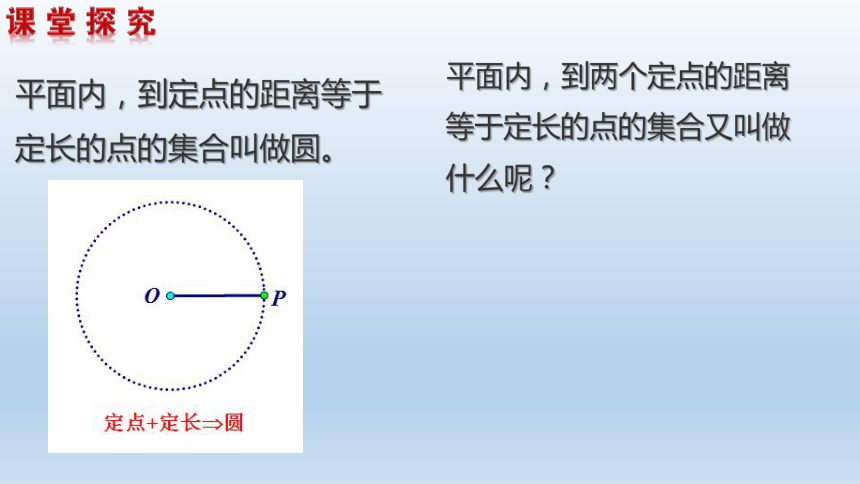
平面内,到定点的距离等于定长的点的集合叫做圆。
平面内,到两个定点的距离等于定长的点的集合又叫做什么呢?
实验操作
(1)取一条定长的细绳;
(2)把它的两端都固定在图板的同一点处;
(3)套上铅笔,拉紧绳子,移动笔尖,这时笔尖(动点)画出的轨迹是一个圆.如果把细绳的两端拉开一段距离,分别固定在图板的两点处套上铅笔,拉紧绳子,移动笔尖,画出的轨迹是椭圆.
根据刚才的实验请同学们回答下面几个题:
1.在画椭圆的过程中,细绳的两端的位置是固定的
还是运动的?
2.在画椭圆的过程中,绳子的长度变了没有?说明
了什么?
3.在画椭圆的过程中,绳子长度与两定点距离大小
有怎样的关系?
椭圆定义:
我们把平面内与两个定点F1,F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆.
两个定点F1,F2叫做椭圆的焦点.
两焦点间的距离|F1F2|叫做椭圆的焦距.
归纳总结
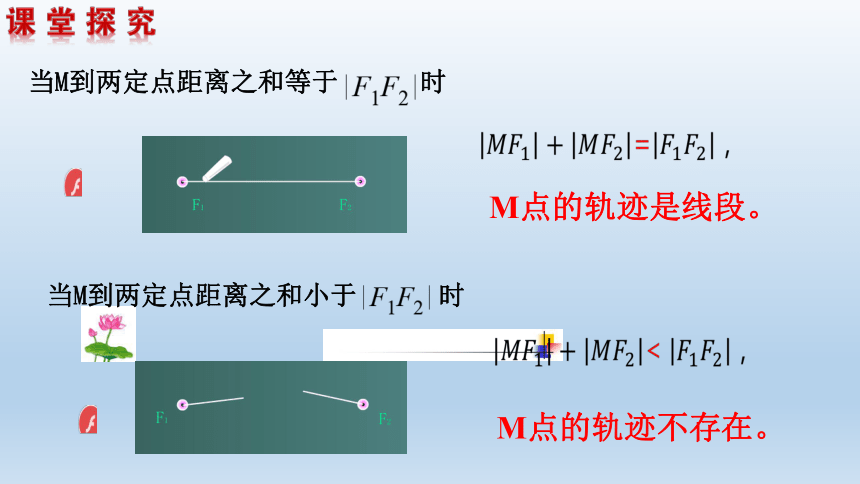
M点的轨迹是线段。
M点的轨迹不存在。
当M到两定点距离之和等于 时
当M到两定点距离之和小于 时
根据椭圆的定义如何求椭圆的方程呢?
思考:求曲线的方程的基本步骤是什么呢?
(1)建系设点;
(2)写出点集;
(3)列出方程;
(4)化简方程;
(5)检验.
O
x
y
M
F1
F2
方案一
F1
F2
方案二
O
x
y
M
如何建立适当的坐标系呢?
x
F1
F2
M
O
y
设M(x, y)是椭圆上任意一点,椭圆的两个焦点分别为F1和F2,椭圆的焦距为2c(c>0),M与F1和F2 的距离的和等于2a(2a>2c>0) .
解:以焦点F1,F2的所在直线为x轴,线段F1F2的垂直平分线为y轴,建立平面直角坐标系xOy(如图).
设M(x, y )是椭圆上任意一点,椭圆的焦距为2c(c>0),M与F1和F2的距离的和等于正常数2a (2a>2c) ,则F1,F2的坐标分别是( c,0)、(c,0) .
限制条件: |MF1|+|MF2|=2a
因为|MF1|= ,|MF2|= ,所以
+
=2a
为化简这个方程,将左边的一个根式移到右边,得
将这个方程两边平方,得
整理得
上式两边在平方,得
整理得
两边同时除以 ,得
=2a-
M
c
a
o
y
x
M
c
a
如果焦点在y轴上,椭圆的方程是什么?
焦点位置 焦点在x轴 焦点在y轴
标准方程
图象
焦点
的关系
椭圆的标准方程
归纳总结
(1)椭圆的标准方程的形式:左边是两个分式
的平方和,右边是1;
(2)椭圆的标准方程中,x2与y2的分母哪一个大,
则焦点在哪一个轴上;
(3)椭圆的标准方程中a,b,c满足a2=b2+c2.
椭圆的标准方程有哪些特征呢?
归纳总结
例1.求下列椭圆的交点坐标及椭圆上任意一点到两焦点的距离之和。
例2:(1)两个焦点的坐标分别为(-4,0)和(4,0),
且椭圆经过(5,0)
(2)焦点在y轴,且椭圆经过(1,0)和(0,2)
(3)椭圆经过(3,-2)和(-6,1)
待定系数法
定义法
B
y
o
F1
F2
M
x
N
6
14
2.填空
1.已知F1,F2是椭圆 的两个焦点,
过F1的直线交椭圆于M,N两点,则三角形
MNF2的周长为( )
A.10 B.20 C.30 D.40
定 义
图
形
方 程
焦 点
F(±c,0)
F(0,±c)
a,b,c
的关系
{P||PF1|+|PF2|=2a,2a>|F1F2|}
1
2
y
o
F
F
P
x
y
x
o
2
F
P
F
1
第三章 圆锥曲线与方程
3.1 椭 圆
3.1.1 椭圆的标准方程
1.了解椭圆的实际背景,感受椭圆在刻画现实世界和解决实际问题中的作用.(重点)
2.掌握椭圆的定义,会求椭圆的标准方程.(重点、难点)
通过图片我们看到,在我们所生活的世界中,随处可见椭圆这种图形,而且我们也已经知道了椭圆的大致形状,那么我们能否动手画一个标准的椭圆呢?
平面内,到定点的距离等于定长的点的集合叫做圆。
平面内,到两个定点的距离等于定长的点的集合又叫做什么呢?
实验操作
(1)取一条定长的细绳;
(2)把它的两端都固定在图板的同一点处;
(3)套上铅笔,拉紧绳子,移动笔尖,这时笔尖(动点)画出的轨迹是一个圆.如果把细绳的两端拉开一段距离,分别固定在图板的两点处套上铅笔,拉紧绳子,移动笔尖,画出的轨迹是椭圆.
根据刚才的实验请同学们回答下面几个题:
1.在画椭圆的过程中,细绳的两端的位置是固定的
还是运动的?
2.在画椭圆的过程中,绳子的长度变了没有?说明
了什么?
3.在画椭圆的过程中,绳子长度与两定点距离大小
有怎样的关系?
椭圆定义:
我们把平面内与两个定点F1,F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆.
两个定点F1,F2叫做椭圆的焦点.
两焦点间的距离|F1F2|叫做椭圆的焦距.
归纳总结
M点的轨迹是线段。
M点的轨迹不存在。
当M到两定点距离之和等于 时
当M到两定点距离之和小于 时
根据椭圆的定义如何求椭圆的方程呢?
思考:求曲线的方程的基本步骤是什么呢?
(1)建系设点;
(2)写出点集;
(3)列出方程;
(4)化简方程;
(5)检验.
O
x
y
M
F1
F2
方案一
F1
F2
方案二
O
x
y
M
如何建立适当的坐标系呢?
x
F1
F2
M
O
y
设M(x, y)是椭圆上任意一点,椭圆的两个焦点分别为F1和F2,椭圆的焦距为2c(c>0),M与F1和F2 的距离的和等于2a(2a>2c>0) .
解:以焦点F1,F2的所在直线为x轴,线段F1F2的垂直平分线为y轴,建立平面直角坐标系xOy(如图).
设M(x, y )是椭圆上任意一点,椭圆的焦距为2c(c>0),M与F1和F2的距离的和等于正常数2a (2a>2c) ,则F1,F2的坐标分别是( c,0)、(c,0) .
限制条件: |MF1|+|MF2|=2a
因为|MF1|= ,|MF2|= ,所以
+
=2a
为化简这个方程,将左边的一个根式移到右边,得
将这个方程两边平方,得
整理得
上式两边在平方,得
整理得
两边同时除以 ,得
=2a-
M
c
a
o
y
x
M
c
a
如果焦点在y轴上,椭圆的方程是什么?
焦点位置 焦点在x轴 焦点在y轴
标准方程
图象
焦点
的关系
椭圆的标准方程
归纳总结
(1)椭圆的标准方程的形式:左边是两个分式
的平方和,右边是1;
(2)椭圆的标准方程中,x2与y2的分母哪一个大,
则焦点在哪一个轴上;
(3)椭圆的标准方程中a,b,c满足a2=b2+c2.
椭圆的标准方程有哪些特征呢?
归纳总结
例1.求下列椭圆的交点坐标及椭圆上任意一点到两焦点的距离之和。
例2:(1)两个焦点的坐标分别为(-4,0)和(4,0),
且椭圆经过(5,0)
(2)焦点在y轴,且椭圆经过(1,0)和(0,2)
(3)椭圆经过(3,-2)和(-6,1)
待定系数法
定义法
B
y
o
F1
F2
M
x
N
6
14
2.填空
1.已知F1,F2是椭圆 的两个焦点,
过F1的直线交椭圆于M,N两点,则三角形
MNF2的周长为( )
A.10 B.20 C.30 D.40
定 义
图
形
方 程
焦 点
F(±c,0)
F(0,±c)
a,b,c
的关系
{P||PF1|+|PF2|=2a,2a>|F1F2|}
1
2
y
o
F
F
P
x
y
x
o
2
F
P
F
1
同课章节目录
