不等式的性质
图片预览





文档简介
课件18张PPT。9.1.2不等式的性质(一)回顾:等式有哪些性质?性质1:等式两边同时加上 (或减去)同一个数(或式子), 结果仍 .
性质2:等式两边同时乘以(或除以)同一个不为0的数,结果仍 .联想:不等式是否有类似的性质?相等相等规律探索不等式两边都加(或减去)
同一个数
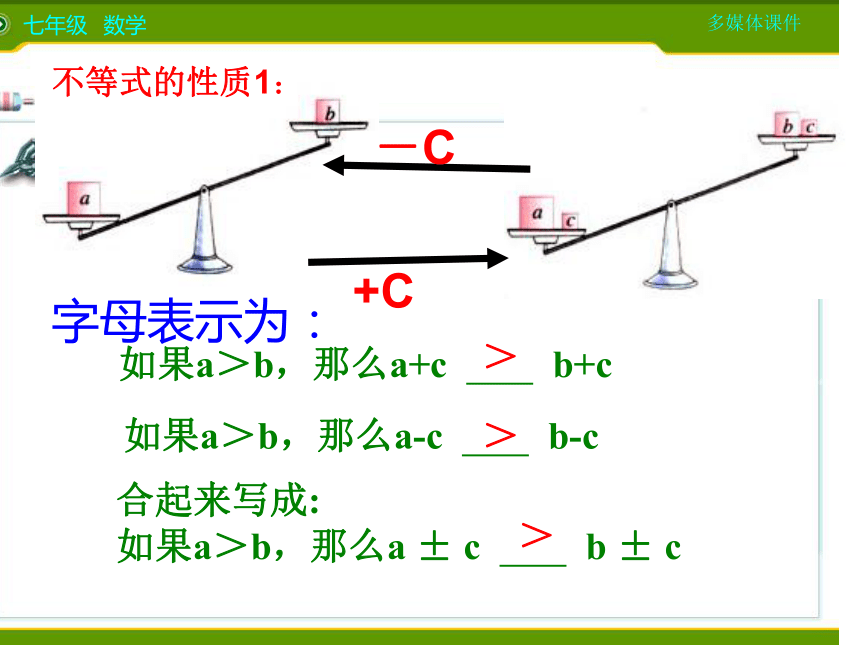
5>3-1<35+2 3+2,>5-2 3-2-1+2 3+2,-1-2 3-2<<不变不变.........不等式性质1:
不等式两边加上(减去)同一个数(或式子),不等号的方向 。>不变(用>或<填空) 如果a>b,那么a+c b+c
字母表示为:+C-C>如果a>b,那么a-c b-c>合起来写成:
如果a>b,那么a ± c b ± c>不等式的性质1:规律探索不等式两边都乘(或除以)
同一个正数
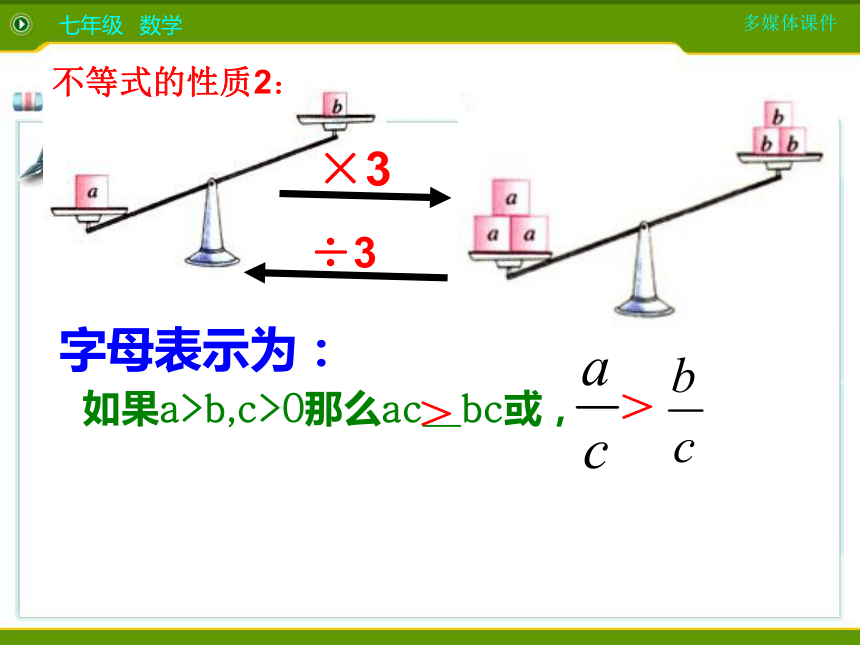
6>26×5 2×5,>不变不变-2<3(-2)÷2 3÷2<.........不等式性质2:
不等式两边乘以(或除以)同一个正数,不等号的方向 。(用>或<填空)不变 如果a>b,c>0那么ac bc或,字母表示为:×3÷3 > > 不等式的性质2: 规律探索不等式两边都乘(或除以)
同一个负数
6>26×(-5) 2×(-5)-2<3-2÷(-1) 3÷(-1)改变改变.........不等式性质3:
不等式两边乘以( 除以)同一个负数,不等号的方向 。(用>或<填空)<>改变如果a>b,c<0
那么ac bc,不等式的性质3,也可以用字母表示为:类似地,﹤﹤ 不等式
性质1:不等式两边加( 减去 )同一个正数,不等号的方向不变。
性质2:不等式两边乘( 或除以 )同一个正数,不等号的方向不变。
性质3: 不等式两边乘( 或除以 )同一个负数,不等号的方向改变。
朗读记忆性质2:不等式两边乘( 或除以 )同一个正数,不等号的方向不变。
性质3: 不等式两边乘( 或除以 )同一个负数,
不等号的方向改变。比较不等式的性质2和性质3,你发现它们有什么区别?针对练习1、设m>n,用“>”或“<”填空:
(1)m-5 n-5(根据不等式的性质 )
(2) m n (根据不等式的性质 )
(3)-6m -6n(根据不等式的性质 )
>1>23<2m-3 2n-3 (5)-3m+1 -3n+1><(1)如果x-5>4,那么两边都加上5,根据不等式的性质 ,可以得到 。
(2)如果 x < 3,那么两边都乘以2,
根据不等式的性质 ,可得到 。针对练习(3)如果-3x>9,那么两边都除以-3,
根据不等式的性质 ,可得到 。填空:利用不等式的性质解下列不等式,并把不等式的解集用数轴表示出来.(课本125页例1)(1)x -7 > 26 (2)3x <2x+1
>50(3)(4)-4x >3方法指导:解不等式时也可以“移项”,请你尝试用“移项”的方法解下列不等式:(1)移项要变号,(2)不等式两边除以同一个负数时,不等号方向要改变。(1)x -7 > 26 (2)3x <2x+1
(3)2x - 3 ≥5x+6想一想:用“移项”的方法解一元一次不等式与解一元一次方程有何相同和不同的地方?自我检测解下列不等式,并把不等式的解集用数轴表示出来 .(1) x+5>-1(3)(2) 5x<3x-8(4) 4x - 1 ≤ 5x+15如果关于x的不等式 (1-a)x>1-a 的解 集为 x<1 ,试确定的取值范围。思维拓展回味无穷本节课你的收获是什么? ※不等式的性质 ※不等式性质的应用
作业:128页:5、6、7
性质2:等式两边同时乘以(或除以)同一个不为0的数,结果仍 .联想:不等式是否有类似的性质?相等相等规律探索不等式两边都加(或减去)
同一个数
5>3-1<35+2 3+2,>5-2 3-2-1+2 3+2,-1-2 3-2<<不变不变.........不等式性质1:
不等式两边加上(减去)同一个数(或式子),不等号的方向 。>不变(用>或<填空) 如果a>b,那么a+c b+c
字母表示为:+C-C>如果a>b,那么a-c b-c>合起来写成:
如果a>b,那么a ± c b ± c>不等式的性质1:规律探索不等式两边都乘(或除以)
同一个正数
6>26×5 2×5,>不变不变-2<3(-2)÷2 3÷2<.........不等式性质2:
不等式两边乘以(或除以)同一个正数,不等号的方向 。(用>或<填空)不变 如果a>b,c>0那么ac bc或,字母表示为:×3÷3 > > 不等式的性质2: 规律探索不等式两边都乘(或除以)
同一个负数
6>26×(-5) 2×(-5)-2<3-2÷(-1) 3÷(-1)改变改变.........不等式性质3:
不等式两边乘以( 除以)同一个负数,不等号的方向 。(用>或<填空)<>改变如果a>b,c<0
那么ac bc,不等式的性质3,也可以用字母表示为:类似地,﹤﹤ 不等式
性质1:不等式两边加( 减去 )同一个正数,不等号的方向不变。
性质2:不等式两边乘( 或除以 )同一个正数,不等号的方向不变。
性质3: 不等式两边乘( 或除以 )同一个负数,不等号的方向改变。
朗读记忆性质2:不等式两边乘( 或除以 )同一个正数,不等号的方向不变。
性质3: 不等式两边乘( 或除以 )同一个负数,
不等号的方向改变。比较不等式的性质2和性质3,你发现它们有什么区别?针对练习1、设m>n,用“>”或“<”填空:
(1)m-5 n-5(根据不等式的性质 )
(2) m n (根据不等式的性质 )
(3)-6m -6n(根据不等式的性质 )
>1>23<2m-3 2n-3 (5)-3m+1 -3n+1><(1)如果x-5>4,那么两边都加上5,根据不等式的性质 ,可以得到 。
(2)如果 x < 3,那么两边都乘以2,
根据不等式的性质 ,可得到 。针对练习(3)如果-3x>9,那么两边都除以-3,
根据不等式的性质 ,可得到 。填空:利用不等式的性质解下列不等式,并把不等式的解集用数轴表示出来.(课本125页例1)(1)x -7 > 26 (2)3x <2x+1
>50(3)(4)-4x >3方法指导:解不等式时也可以“移项”,请你尝试用“移项”的方法解下列不等式:(1)移项要变号,(2)不等式两边除以同一个负数时,不等号方向要改变。(1)x -7 > 26 (2)3x <2x+1
(3)2x - 3 ≥5x+6想一想:用“移项”的方法解一元一次不等式与解一元一次方程有何相同和不同的地方?自我检测解下列不等式,并把不等式的解集用数轴表示出来 .(1) x+5>-1(3)(2) 5x<3x-8(4) 4x - 1 ≤ 5x+15如果关于x的不等式 (1-a)x>1-a 的解 集为 x<1 ,试确定的取值范围。思维拓展回味无穷本节课你的收获是什么? ※不等式的性质 ※不等式性质的应用
作业:128页:5、6、7
