华师大版数学(2024)七年级下册期末复习题(精华)(含答案)
文档属性
| 名称 | 华师大版数学(2024)七年级下册期末复习题(精华)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1005.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-13 16:42:56 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
华师大版数学(2024)七年级下册期末复习题(精华)
一、单选题
1.若,则下列各式中一定成立的是( )
A. B. C. D.
2.关于x的一元一次不等式x﹣3<0的解集在数轴上表示为( )
A. B.
C. D.
3.下列图形中,是轴对称图形不是中心对称图形的是( )
A. B.
C. D.
4.某条河道水流速度为每小时2千米,一艘渔船从地出发顺流航行到地,再调头逆流航行到、之间的地共用了6小时(掉头时间忽略不计),若渔船顺水速度是逆水速度的3倍,且、两地的距离为20千米,则、两地的距离为( )
A.2千米 B.4千米 C.6千米 D.8千米
5.已知正多边形的一个外角等于,则该正多边形的边数为( )
A.十 B.九 C.八 D.七
6.已知关于x,y的方程组,则下列结论中正确的是( )
①当时,方程组的解也是方程的解;②当时,;③当时,;④不论a取什么实数,的值始终不变.
A.①② B.①②③ C.②③④ D.①③④
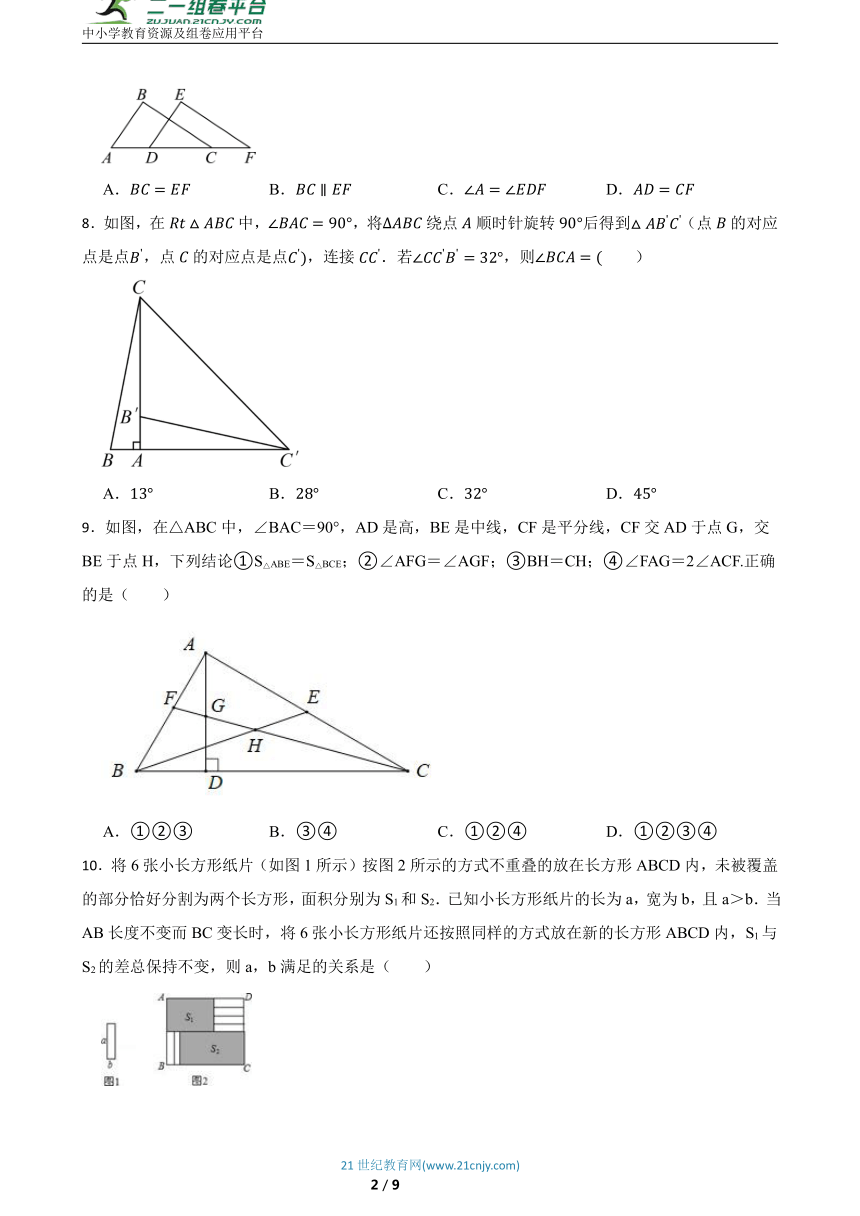
7.如图,已知点、、、在同一条直线上,,,添加一个条件仍无法证明是( )
A. B. C. D.
8.如图,在中,,将绕点顺时针旋转后得到(点的对应点是点,点的对应点是点,连接.若,则 )
A. B. C. D.
9.如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是平分线,CF交AD于点G,交BE于点H,下列结论①S△ABE=S△BCE;②∠AFG=∠AGF;③BH=CH;④∠FAG=2∠ACF.正确的是( )
A.①②③ B.③④ C.①②④ D.①②③④
10.将6张小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好分割为两个长方形,面积分别为S1和S2.已知小长方形纸片的长为a,宽为b,且a>b.当AB长度不变而BC变长时,将6张小长方形纸片还按照同样的方式放在新的长方形ABCD内,S1与S2的差总保持不变,则a,b满足的关系是( )
A.b= a B.b= C.b= D.b=
二、填空题
11.如图,,,垂足分别为,,添加一个条件 ,可得.
12.题干纠为:在我国古代数学著作《九章算术》中记载:“今有大器五小器一容三斛,大器一小器五容二斛.问大小器各容几何.”其大意为:有大小两种盛酒的桶,已知五个大桶和一个小桶共可盛酒3斛(斛:古代是一种容量单位),一个大桶和五个小桶共可盛酒2斛,问一个大桶和一个小桶各可以盛酒几斛?若设一个大桶可以盛酒x斛,一个小桶可盛酒y斛,根据题意,可列方程组: .
13.某车间有26名工人,每人每天可以生产800个螺栓或1000个螺母,1个螺栓需要配2个螺母,为使每天生产的螺栓和螺母刚好配套,设安排x名工人生产螺栓,则所列方程为 .
14.如图,在△ABC中,AB=BC,BE、CF分别是AC、AB边上的高,在BE上取点D,使BD=CA,在射线CF上取点G,使CG=BA,连接AD、AG,若∠DAE=38°,∠EBC=20°,则∠GAB= °.
15.正多边形的一个外角是72°,则这个多边形的内角和的度数是 .
16.对于任意实数m、n,定义一种运运算m※n=mn﹣m﹣n+3,等式的右边是通常的加减和乘法运算,例如:3※5=3×5﹣3﹣5+3=10.请根据上述定义解决问题:若a<2※x<7,且解集中有两个整数解,则a的取值范围是
三、计算题
17.解下列不等式,并把解表示在数轴上.
(1)
(2)
(3)
(4)
18.解下列方程
(1)2(3x-1)-2x=3-x;
(2)
19.(1)小明爸爸上周买进某种股票1000股,每股27.3元,下表为本周每天该股票的涨跌情况:
星期 一 二 三 四 五
每股涨跌 +1 +1.5 ﹣1.5 ﹣2.5 +0.5
①星期三收盘时,每股是多少元?
②本周内最高价是每股多少元?最低价是每股多少元?
③若小明爸爸按本周五的收盘价将股票全部卖出,你认为他会获利吗?
(2)国家规定个人发表文章、出版图书所得稿费的纳税计算方法是:
①稿费不高于800元的不纳税:
②稿费高于800元,而低于4000元的应缴纳超过800元的那部分稿费的14%的税;
③稿费为4000元或高于4000元的应缴纳全部稿费的11%的税;
若王老师获得稿费后纳税420元,求这笔稿费是多少钱?
四、解答题
20.有若干张长为30、宽为15的长方形白纸,按如图所示的方法黏合起来,黏合部分宽为3.
(1)根据上图,将表格补充完整:
白纸张数 1 2 3 4 … 10 …
纸条长度 30
84 111 …
…
(2)设x张白纸黏合后的总长度为ycm,则y与x之间的关系式是什么?
(3)按照上述黏合方式,你认为至少需要多少张白纸,才能使得黏合起来总长度达到或超过2023
?
21.解方程:
(1);
(2).
22.从甲地到乙地,长途汽车原需行驶7小时,开通高速公路后,路程缩短了30千米,而车速平均每小时增加30千米,这样只需4小时即可到达.求甲、乙两地之间高速公路的路程.
23.如图,已知在数轴上有A、B两点,点A表示的数是﹣6,点B表示的数是9.点P在数轴上从点A出发,以每秒2个单位的速度沿数轴正方向运动,同时,点Q在数轴上从点B出发,以每秒3个单位的速度沿数轴负方向运动,当点Q到达点A时,两点同时停止运动.设运动时间为t秒.
(1)求AB的距离;
(2)当t=1时,点P、点Q分别表示什么数?
(3)当t为何值时,P,Q两点相距5个单位?
24.为选派一支代表队参加云南省第三届“彩云杯”中华优秀传统文化知识竞赛,某中学在三个年级中各选出5名学生组成一支代表队,并在老师的组织下先进行一次知识竞赛.竞赛规则是:每队都必须回答50道题,答对一题得4分,不答或答错一题倒扣1分,如果七年级代表队最后的得分为190分,那么七年级代表队回答对了多少道题?
25.在平面直角坐标系中,点,,是抛物线上的点,.
(1)当,时,求和的值;
(2)若时,,求的取值范围.
答案解析部分
1.【答案】B
【知识点】不等式的性质
2.【答案】C
【知识点】解一元一次不等式;在数轴上表示不等式的解集
3.【答案】B
【知识点】轴对称图形;中心对称及中心对称图形
4.【答案】B
【知识点】一元一次方程的实际应用-行程问题
5.【答案】B
【知识点】多边形内角与外角
6.【答案】C
【知识点】解二元一次方程组;解一元一次不等式;加减消元法解二元一次方程组
7.【答案】D
【知识点】三角形全等的判定
8.【答案】A
【知识点】三角形的外角性质;旋转的性质
9.【答案】C
【知识点】三角形的角平分线、中线和高;三角形的面积;三角形的外角性质;角平分线的概念
10.【答案】D
【知识点】整式的加减运算;一元一次方程的实际应用-几何问题
11.【答案】AB=AD或BC=DC
【知识点】三角形全等的判定
12.【答案】
【知识点】列二元一次方程组
13.【答案】2×800x=1000(26-x)
【知识点】列一元一次方程
14.【答案】58
【知识点】三角形全等的判定-SAS
15.【答案】540°
【知识点】多边形内角与外角
16.【答案】4≤a<5
【知识点】一元一次不等式组的应用
17.【答案】(1)解:
解得:x<2,
将解表示在数轴上,如图:
(2)解:
解得:x>-13
将解表示在数轴上,如图:
(3)解:
解得:
将解表示在数轴上,如图:
(4)解:
解得:
将解表示在数轴上,如图:
【知识点】解一元一次不等式;在数轴上表示不等式的解集
18.【答案】(1)解:去括号,得6x-2-2x=3-x,
移项,得6x-2x+x=3+2,
合并同类项,得5x=5,
系数化为1,得x=1;
(2)解:去分母得:5(3x-1)=2(4x+2)-10,
去括号得:15x-5=8x+4-10,
移项得:15x-8x=4-10+5,
合并同类项得:7x=-1,
系数化为1得:x=-.
【知识点】解含括号的一元一次方程;解含分数系数的一元一次方程
19.【答案】(1)①28.3;②本周内最高价是每股29.8元,最低价是每股25.8元;③周五的收盘价时卖出,不会获利,会亏本;(2)王老师的稿费是3800元.
【知识点】一元一次方程的其他应用
20.【答案】(1)57;273
(2)
(3)至少需要75张白纸,才能使得黏合起来总长度达到或超过2023
【知识点】一元一次方程的其他应用
21.【答案】(1)
(2)
【知识点】解一元一次方程;解含括号的一元一次方程;解含分数系数的一元一次方程
22.【答案】解:设甲、乙两地之间高速公路的路程为x千米,
根据题意得:,
解得x=320,
答:甲、乙两地之间高速公路的路程为320千米.
【知识点】一元一次方程的实际应用-行程问题
23.【答案】解:(1) 点A表示的数是﹣6,点B表示的数是9,
(2)当时,点P对应的数为:
点Q对应的数为:
(3)设运动s后,则对应的数为对应的数为
,
或
解得:或
点Q到达点A时,运动时间为s,
所以当运动时间为4s或2s时,之间的距离为5.
【知识点】一元一次方程的实际应用-几何问题;数轴上两点之间的距离
24.【答案】解:设七年级代表队回答对了x道题,
根据题意列方程:4x-(50-x)=190,
解这个方程得:x=48.
故七年级代表队回答对了48道题.
【知识点】一元一次方程的实际应用-积分问题
25.【答案】(1),
(2)或
【知识点】解二元一次方程组;解一元一次不等式
21世纪教育网(www.21cnjy.com)
2 / 9
华师大版数学(2024)七年级下册期末复习题(精华)
一、单选题
1.若,则下列各式中一定成立的是( )
A. B. C. D.
2.关于x的一元一次不等式x﹣3<0的解集在数轴上表示为( )
A. B.
C. D.
3.下列图形中,是轴对称图形不是中心对称图形的是( )
A. B.
C. D.
4.某条河道水流速度为每小时2千米,一艘渔船从地出发顺流航行到地,再调头逆流航行到、之间的地共用了6小时(掉头时间忽略不计),若渔船顺水速度是逆水速度的3倍,且、两地的距离为20千米,则、两地的距离为( )
A.2千米 B.4千米 C.6千米 D.8千米
5.已知正多边形的一个外角等于,则该正多边形的边数为( )
A.十 B.九 C.八 D.七
6.已知关于x,y的方程组,则下列结论中正确的是( )
①当时,方程组的解也是方程的解;②当时,;③当时,;④不论a取什么实数,的值始终不变.
A.①② B.①②③ C.②③④ D.①③④
7.如图,已知点、、、在同一条直线上,,,添加一个条件仍无法证明是( )
A. B. C. D.
8.如图,在中,,将绕点顺时针旋转后得到(点的对应点是点,点的对应点是点,连接.若,则 )
A. B. C. D.
9.如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是平分线,CF交AD于点G,交BE于点H,下列结论①S△ABE=S△BCE;②∠AFG=∠AGF;③BH=CH;④∠FAG=2∠ACF.正确的是( )
A.①②③ B.③④ C.①②④ D.①②③④
10.将6张小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好分割为两个长方形,面积分别为S1和S2.已知小长方形纸片的长为a,宽为b,且a>b.当AB长度不变而BC变长时,将6张小长方形纸片还按照同样的方式放在新的长方形ABCD内,S1与S2的差总保持不变,则a,b满足的关系是( )
A.b= a B.b= C.b= D.b=
二、填空题
11.如图,,,垂足分别为,,添加一个条件 ,可得.
12.题干纠为:在我国古代数学著作《九章算术》中记载:“今有大器五小器一容三斛,大器一小器五容二斛.问大小器各容几何.”其大意为:有大小两种盛酒的桶,已知五个大桶和一个小桶共可盛酒3斛(斛:古代是一种容量单位),一个大桶和五个小桶共可盛酒2斛,问一个大桶和一个小桶各可以盛酒几斛?若设一个大桶可以盛酒x斛,一个小桶可盛酒y斛,根据题意,可列方程组: .
13.某车间有26名工人,每人每天可以生产800个螺栓或1000个螺母,1个螺栓需要配2个螺母,为使每天生产的螺栓和螺母刚好配套,设安排x名工人生产螺栓,则所列方程为 .
14.如图,在△ABC中,AB=BC,BE、CF分别是AC、AB边上的高,在BE上取点D,使BD=CA,在射线CF上取点G,使CG=BA,连接AD、AG,若∠DAE=38°,∠EBC=20°,则∠GAB= °.
15.正多边形的一个外角是72°,则这个多边形的内角和的度数是 .
16.对于任意实数m、n,定义一种运运算m※n=mn﹣m﹣n+3,等式的右边是通常的加减和乘法运算,例如:3※5=3×5﹣3﹣5+3=10.请根据上述定义解决问题:若a<2※x<7,且解集中有两个整数解,则a的取值范围是
三、计算题
17.解下列不等式,并把解表示在数轴上.
(1)
(2)
(3)
(4)
18.解下列方程
(1)2(3x-1)-2x=3-x;
(2)
19.(1)小明爸爸上周买进某种股票1000股,每股27.3元,下表为本周每天该股票的涨跌情况:
星期 一 二 三 四 五
每股涨跌 +1 +1.5 ﹣1.5 ﹣2.5 +0.5
①星期三收盘时,每股是多少元?
②本周内最高价是每股多少元?最低价是每股多少元?
③若小明爸爸按本周五的收盘价将股票全部卖出,你认为他会获利吗?
(2)国家规定个人发表文章、出版图书所得稿费的纳税计算方法是:
①稿费不高于800元的不纳税:
②稿费高于800元,而低于4000元的应缴纳超过800元的那部分稿费的14%的税;
③稿费为4000元或高于4000元的应缴纳全部稿费的11%的税;
若王老师获得稿费后纳税420元,求这笔稿费是多少钱?
四、解答题
20.有若干张长为30、宽为15的长方形白纸,按如图所示的方法黏合起来,黏合部分宽为3.
(1)根据上图,将表格补充完整:
白纸张数 1 2 3 4 … 10 …
纸条长度 30
84 111 …
…
(2)设x张白纸黏合后的总长度为ycm,则y与x之间的关系式是什么?
(3)按照上述黏合方式,你认为至少需要多少张白纸,才能使得黏合起来总长度达到或超过2023
?
21.解方程:
(1);
(2).
22.从甲地到乙地,长途汽车原需行驶7小时,开通高速公路后,路程缩短了30千米,而车速平均每小时增加30千米,这样只需4小时即可到达.求甲、乙两地之间高速公路的路程.
23.如图,已知在数轴上有A、B两点,点A表示的数是﹣6,点B表示的数是9.点P在数轴上从点A出发,以每秒2个单位的速度沿数轴正方向运动,同时,点Q在数轴上从点B出发,以每秒3个单位的速度沿数轴负方向运动,当点Q到达点A时,两点同时停止运动.设运动时间为t秒.
(1)求AB的距离;
(2)当t=1时,点P、点Q分别表示什么数?
(3)当t为何值时,P,Q两点相距5个单位?
24.为选派一支代表队参加云南省第三届“彩云杯”中华优秀传统文化知识竞赛,某中学在三个年级中各选出5名学生组成一支代表队,并在老师的组织下先进行一次知识竞赛.竞赛规则是:每队都必须回答50道题,答对一题得4分,不答或答错一题倒扣1分,如果七年级代表队最后的得分为190分,那么七年级代表队回答对了多少道题?
25.在平面直角坐标系中,点,,是抛物线上的点,.
(1)当,时,求和的值;
(2)若时,,求的取值范围.
答案解析部分
1.【答案】B
【知识点】不等式的性质
2.【答案】C
【知识点】解一元一次不等式;在数轴上表示不等式的解集
3.【答案】B
【知识点】轴对称图形;中心对称及中心对称图形
4.【答案】B
【知识点】一元一次方程的实际应用-行程问题
5.【答案】B
【知识点】多边形内角与外角
6.【答案】C
【知识点】解二元一次方程组;解一元一次不等式;加减消元法解二元一次方程组
7.【答案】D
【知识点】三角形全等的判定
8.【答案】A
【知识点】三角形的外角性质;旋转的性质
9.【答案】C
【知识点】三角形的角平分线、中线和高;三角形的面积;三角形的外角性质;角平分线的概念
10.【答案】D
【知识点】整式的加减运算;一元一次方程的实际应用-几何问题
11.【答案】AB=AD或BC=DC
【知识点】三角形全等的判定
12.【答案】
【知识点】列二元一次方程组
13.【答案】2×800x=1000(26-x)
【知识点】列一元一次方程
14.【答案】58
【知识点】三角形全等的判定-SAS
15.【答案】540°
【知识点】多边形内角与外角
16.【答案】4≤a<5
【知识点】一元一次不等式组的应用
17.【答案】(1)解:
解得:x<2,
将解表示在数轴上,如图:
(2)解:
解得:x>-13
将解表示在数轴上,如图:
(3)解:
解得:
将解表示在数轴上,如图:
(4)解:
解得:
将解表示在数轴上,如图:
【知识点】解一元一次不等式;在数轴上表示不等式的解集
18.【答案】(1)解:去括号,得6x-2-2x=3-x,
移项,得6x-2x+x=3+2,
合并同类项,得5x=5,
系数化为1,得x=1;
(2)解:去分母得:5(3x-1)=2(4x+2)-10,
去括号得:15x-5=8x+4-10,
移项得:15x-8x=4-10+5,
合并同类项得:7x=-1,
系数化为1得:x=-.
【知识点】解含括号的一元一次方程;解含分数系数的一元一次方程
19.【答案】(1)①28.3;②本周内最高价是每股29.8元,最低价是每股25.8元;③周五的收盘价时卖出,不会获利,会亏本;(2)王老师的稿费是3800元.
【知识点】一元一次方程的其他应用
20.【答案】(1)57;273
(2)
(3)至少需要75张白纸,才能使得黏合起来总长度达到或超过2023
【知识点】一元一次方程的其他应用
21.【答案】(1)
(2)
【知识点】解一元一次方程;解含括号的一元一次方程;解含分数系数的一元一次方程
22.【答案】解:设甲、乙两地之间高速公路的路程为x千米,
根据题意得:,
解得x=320,
答:甲、乙两地之间高速公路的路程为320千米.
【知识点】一元一次方程的实际应用-行程问题
23.【答案】解:(1) 点A表示的数是﹣6,点B表示的数是9,
(2)当时,点P对应的数为:
点Q对应的数为:
(3)设运动s后,则对应的数为对应的数为
,
或
解得:或
点Q到达点A时,运动时间为s,
所以当运动时间为4s或2s时,之间的距离为5.
【知识点】一元一次方程的实际应用-几何问题;数轴上两点之间的距离
24.【答案】解:设七年级代表队回答对了x道题,
根据题意列方程:4x-(50-x)=190,
解这个方程得:x=48.
故七年级代表队回答对了48道题.
【知识点】一元一次方程的实际应用-积分问题
25.【答案】(1),
(2)或
【知识点】解二元一次方程组;解一元一次不等式
21世纪教育网(www.21cnjy.com)
2 / 9
同课章节目录
