华师大版数学(2024)七年级下册期末复习题(培优)(含答案)
文档属性
| 名称 | 华师大版数学(2024)七年级下册期末复习题(培优)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 264.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-13 16:54:20 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
华师大版数学(2024)七年级下册期末复习题(培优)
一、单选题
1.(2024八上·杭州期中)下列不等式变形正确的是( )
A.由,得 B.由,得
C.由,得 D.由,得
2.(2024九下·咸宁模拟)在数轴上表示不等式的解集,正确的是( )
A. B.
C. D.
3.(2024九上·密云期中)在圆、正方形、平行四边形、等边三角形这四个图形中,既是轴对称图形又是中心对称图形的图形个数是( )
A.1个 B.2个 C.3个 D.4个
4.(2024七上·交城期末)中国“最美扶贫高铁”之一的“张吉怀高铁”开通后,张家界到怀化的运行时间由原来的3.5小时缩短到1小时,运行里程缩短了40千米.已知高铁的平均速度比普通列车的平均速度每小时快200千米,求高铁的平均速度.若设高铁的平均速度为千米/时.则下列方程正确的是( )
A. B.
C. D.
5.(2024九上·思茅期中)一个多边形的内角和是外角和的6倍,则这个多边形的边数是( )
A.11 B.12 C.13 D.14
6.(2024七下·商水期中)已知关于x,y的二元一次方程组有下列说法:
①当时,;
②当x与y互为相反数时,解得;
③当时,;
④无论k为何值,x与y的值一定满足关系式,其中正确的是( )
A.①②③ B.①②④ C.①③④ D.①②③④
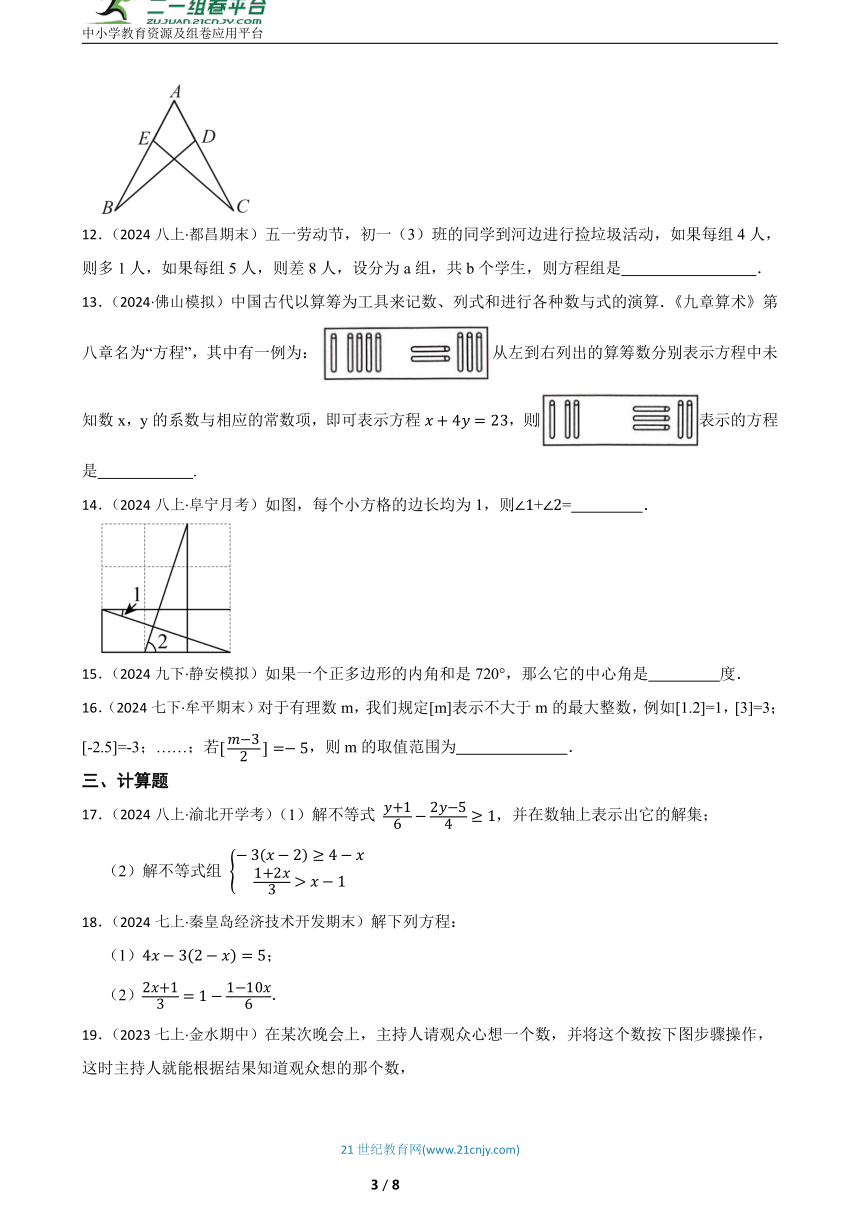
7.(2024八上·株洲月考)如图所示,在和中,点A,E,B,D在同一直线上,,,只添加一个条件,能判定的是( )
A. B. C. D.
8.(2024九上·鹤山月考)如图,在中,,将绕点顺时针旋转后得到(点的对应点是点,点的对应点是点).连接,若,则的大小是( )
A. B. C. D.
9.(2023七下·宿迁期中)如图,在中,,是高,是角平分线,是中线,交于点G,交于点H,以下结论:①的面积的面积;②;③;④;其中正确的结论个数是( )
A.3个 B.2个 C.1个 D.4个
10.(2024七上·无棣期末)互不重合的A,B,C三点在同一直线上,已知,,,,则这三点的位置关系是( )
A.点A在B、C两点之间 B.点C在A、B两点之间
C.点B在A、C两点之间 D.无法确定
二、填空题
11.(2024八上·蕲春期中)如图,点D、E分别在、上,已知,要使,还需要添加一个条件,你添加的条件是 .(只需写一个,不添加辅助线)
12.(2024八上·都昌期末)五一劳动节,初一(3)班的同学到河边进行捡垃圾活动,如果每组4人,则多1人,如果每组5人,则差8人,设分为a组,共b个学生,则方程组是 .
13.(2024·佛山模拟)中国古代以算筹为工具来记数、列式和进行各种数与式的演算.《九章算术》第八章名为“方程”,其中有一例为:从左到右列出的算筹数分别表示方程中未知数x,y的系数与相应的常数项,即可表示方程,则表示的方程是 .
14.(2024八上·阜宁月考)如图,每个小方格的边长均为1,则+= .
15.(2024九下·静安模拟)如果一个正多边形的内角和是720°,那么它的中心角是 度.
16.(2024七下·牟平期末)对于有理数m,我们规定[m]表示不大于m的最大整数,例如[1.2]=1,[3]=3;[-2.5]=-3;……;若,则m的取值范围为 .
三、计算题
17.(2024八上·渝北开学考)(1)解不等式 并在数轴上表示出它的解集;
(2)解不等式组
18.(2024七上·秦皇岛经济技术开发期末)解下列方程:
(1);
(2).
19.(2023七上·金水期中)在某次晚会上,主持人请观众心想一个数,并将这个数按下图步骤操作,这时主持人就能根据结果知道观众想的那个数,
(1)小玲心想的数是,求出按照步骤操作的结果
(2)小明心想了一个数,并按步骤计算后为2024,你知道小明心想的是哪个数吗?
四、解答题
20.(2023七下·龙湖期中)在平面直角坐标系xOy中,对于P,Q两点给出如下定义:|P|表示点P到x、y轴的距离中的最大值,|Q|表示点Q到x、y轴的距离中的最大值,若,则称P,Q两点为“等距点”.例如:如图中的P(3,3),Q(﹣3,﹣2)两点,有|P|=|Q|=3,所以P、Q两点为“等距点”.
(1)已知点A的坐标为(﹣3,1),
①则点A到x、y轴的距离中的最大值|A|= ;
②在点E(0,3),F(3,﹣3),G(2,﹣5)中,为点A的“等距点”的是 ;
③若点B的坐标为B(m,m+6),且A,B两点为“等距点”,则点B的坐标为 ;
(2)若,且|4k﹣3|≤4,两点为“等距点”,求k的值.
21.(2023八上·湖北月考)解方程:
(1);
(2).
22.(2023七上·青山湖月考)一艘船从甲码头到乙码头顺流航行,用了3.2h,从乙码头返回甲码头逆流航行,用了4.8h,已知水流的速度为3km/h,求这艘船在静水中的速度.
23.(2024七下·朝阳期中)已知在数轴上,点、、分别表示、、.
(1)当点与点重合时,求的值.
(2)在点、、中,任意两点互不重合,若其中一点到另外两点的距离相等,求的值.
(3)若点到点的距离小于点到点的距离,直接写出的取值范围.
24.(2024九下·玄武模拟)某磁性飞镖游戏的靶盘如图.珍珍玩了两局,每局投10次飞镖,若投到边界则不计入次数,需重新投,计分规则如下:
投中位置 A区 B区 脱靶
一次计分(分) 3 1
在第一局中,珍珍投中A区4次,B区2次,脱靶4次.
(1)求珍珍第一局的得分;
(2)第二局,珍珍投中A区k次,B区3次,其余全部脱靶.若本局得分比第一局提高了13分,求k的值.
25.(2023七下·邹平期末)按要求完成下列题目:
(1)解方程组:
(2)已知方程组的解x,y满足,求m的取值范围.
答案解析部分
1.【答案】B
【知识点】不等式的性质
2.【答案】C
【知识点】解一元一次不等式;在数轴上表示不等式的解集
3.【答案】B
【知识点】轴对称图形;中心对称及中心对称图形
4.【答案】C
【知识点】一元一次方程的实际应用-行程问题
5.【答案】D
【知识点】多边形内角与外角;一元一次方程的实际应用-几何问题
6.【答案】D
【知识点】解二元一次方程组;解一元一次不等式;代入消元法解二元一次方程组;加减消元法解二元一次方程组
7.【答案】A
【知识点】三角形全等的判定
8.【答案】D
【知识点】三角形的外角性质;等腰三角形的性质;旋转的性质
9.【答案】A
【知识点】三角形的角平分线、中线和高;三角形的面积;三角形的外角性质;角平分线的概念
10.【答案】C
【知识点】整式的加减运算;一元一次方程的实际应用-几何问题;线段的和、差、倍、分的简单计算
11.【答案】(答案不唯一)
【知识点】三角形全等的判定
12.【答案】
【知识点】列二元一次方程组
13.【答案】
【知识点】列一元一次方程
14.【答案】
【知识点】三角形全等的判定-SAS
15.【答案】
【知识点】多边形内角与外角;圆内接正多边形
16.【答案】-7≤m<-5
【知识点】解一元一次不等式组;一元一次不等式组的应用
17.【答案】解:(1)去分母得,
去括号得,
移项合并同类项得,
系数化为1得,;
在数轴上表示如下:
(2)
解不等式①得,
解不等式②得,
∴不等式组的解集为
【知识点】解一元一次不等式;解一元一次不等式组;在数轴上表示不等式的解集
18.【答案】(1)
(2)
【知识点】解含括号的一元一次方程;解含分数系数的一元一次方程
19.【答案】(1)
(2)226
【知识点】一元一次方程的其他应用;求代数式的值-程序框图
20.【答案】(1)①3;②E;F;③( 3,3)
(2)k的值是1
【知识点】一元一次方程的其他应用;点的坐标;绝对值的概念与意义
21.【答案】(1)
(2)
【知识点】解一元一次方程;解含括号的一元一次方程;解含分数系数的一元一次方程
22.【答案】船在静水中的速度为km/h.
【知识点】一元一次方程的实际应用-行程问题
23.【答案】(1)
(2)或或
(3)或
【知识点】一元一次不等式的应用;一元一次方程的实际应用-几何问题;数轴上两点之间的距离
24.【答案】(1)珍珍第一局的得分为6分;
(2).
【知识点】一元一次方程的实际应用-积分问题
25.【答案】(1)
(2)
【知识点】解二元一次方程组;解一元一次不等式;代入消元法解二元一次方程组
21世纪教育网(www.21cnjy.com)
1 / 8
华师大版数学(2024)七年级下册期末复习题(培优)
一、单选题
1.(2024八上·杭州期中)下列不等式变形正确的是( )
A.由,得 B.由,得
C.由,得 D.由,得
2.(2024九下·咸宁模拟)在数轴上表示不等式的解集,正确的是( )
A. B.
C. D.
3.(2024九上·密云期中)在圆、正方形、平行四边形、等边三角形这四个图形中,既是轴对称图形又是中心对称图形的图形个数是( )
A.1个 B.2个 C.3个 D.4个
4.(2024七上·交城期末)中国“最美扶贫高铁”之一的“张吉怀高铁”开通后,张家界到怀化的运行时间由原来的3.5小时缩短到1小时,运行里程缩短了40千米.已知高铁的平均速度比普通列车的平均速度每小时快200千米,求高铁的平均速度.若设高铁的平均速度为千米/时.则下列方程正确的是( )
A. B.
C. D.
5.(2024九上·思茅期中)一个多边形的内角和是外角和的6倍,则这个多边形的边数是( )
A.11 B.12 C.13 D.14
6.(2024七下·商水期中)已知关于x,y的二元一次方程组有下列说法:
①当时,;
②当x与y互为相反数时,解得;
③当时,;
④无论k为何值,x与y的值一定满足关系式,其中正确的是( )
A.①②③ B.①②④ C.①③④ D.①②③④
7.(2024八上·株洲月考)如图所示,在和中,点A,E,B,D在同一直线上,,,只添加一个条件,能判定的是( )
A. B. C. D.
8.(2024九上·鹤山月考)如图,在中,,将绕点顺时针旋转后得到(点的对应点是点,点的对应点是点).连接,若,则的大小是( )
A. B. C. D.
9.(2023七下·宿迁期中)如图,在中,,是高,是角平分线,是中线,交于点G,交于点H,以下结论:①的面积的面积;②;③;④;其中正确的结论个数是( )
A.3个 B.2个 C.1个 D.4个
10.(2024七上·无棣期末)互不重合的A,B,C三点在同一直线上,已知,,,,则这三点的位置关系是( )
A.点A在B、C两点之间 B.点C在A、B两点之间
C.点B在A、C两点之间 D.无法确定
二、填空题
11.(2024八上·蕲春期中)如图,点D、E分别在、上,已知,要使,还需要添加一个条件,你添加的条件是 .(只需写一个,不添加辅助线)
12.(2024八上·都昌期末)五一劳动节,初一(3)班的同学到河边进行捡垃圾活动,如果每组4人,则多1人,如果每组5人,则差8人,设分为a组,共b个学生,则方程组是 .
13.(2024·佛山模拟)中国古代以算筹为工具来记数、列式和进行各种数与式的演算.《九章算术》第八章名为“方程”,其中有一例为:从左到右列出的算筹数分别表示方程中未知数x,y的系数与相应的常数项,即可表示方程,则表示的方程是 .
14.(2024八上·阜宁月考)如图,每个小方格的边长均为1,则+= .
15.(2024九下·静安模拟)如果一个正多边形的内角和是720°,那么它的中心角是 度.
16.(2024七下·牟平期末)对于有理数m,我们规定[m]表示不大于m的最大整数,例如[1.2]=1,[3]=3;[-2.5]=-3;……;若,则m的取值范围为 .
三、计算题
17.(2024八上·渝北开学考)(1)解不等式 并在数轴上表示出它的解集;
(2)解不等式组
18.(2024七上·秦皇岛经济技术开发期末)解下列方程:
(1);
(2).
19.(2023七上·金水期中)在某次晚会上,主持人请观众心想一个数,并将这个数按下图步骤操作,这时主持人就能根据结果知道观众想的那个数,
(1)小玲心想的数是,求出按照步骤操作的结果
(2)小明心想了一个数,并按步骤计算后为2024,你知道小明心想的是哪个数吗?
四、解答题
20.(2023七下·龙湖期中)在平面直角坐标系xOy中,对于P,Q两点给出如下定义:|P|表示点P到x、y轴的距离中的最大值,|Q|表示点Q到x、y轴的距离中的最大值,若,则称P,Q两点为“等距点”.例如:如图中的P(3,3),Q(﹣3,﹣2)两点,有|P|=|Q|=3,所以P、Q两点为“等距点”.
(1)已知点A的坐标为(﹣3,1),
①则点A到x、y轴的距离中的最大值|A|= ;
②在点E(0,3),F(3,﹣3),G(2,﹣5)中,为点A的“等距点”的是 ;
③若点B的坐标为B(m,m+6),且A,B两点为“等距点”,则点B的坐标为 ;
(2)若,且|4k﹣3|≤4,两点为“等距点”,求k的值.
21.(2023八上·湖北月考)解方程:
(1);
(2).
22.(2023七上·青山湖月考)一艘船从甲码头到乙码头顺流航行,用了3.2h,从乙码头返回甲码头逆流航行,用了4.8h,已知水流的速度为3km/h,求这艘船在静水中的速度.
23.(2024七下·朝阳期中)已知在数轴上,点、、分别表示、、.
(1)当点与点重合时,求的值.
(2)在点、、中,任意两点互不重合,若其中一点到另外两点的距离相等,求的值.
(3)若点到点的距离小于点到点的距离,直接写出的取值范围.
24.(2024九下·玄武模拟)某磁性飞镖游戏的靶盘如图.珍珍玩了两局,每局投10次飞镖,若投到边界则不计入次数,需重新投,计分规则如下:
投中位置 A区 B区 脱靶
一次计分(分) 3 1
在第一局中,珍珍投中A区4次,B区2次,脱靶4次.
(1)求珍珍第一局的得分;
(2)第二局,珍珍投中A区k次,B区3次,其余全部脱靶.若本局得分比第一局提高了13分,求k的值.
25.(2023七下·邹平期末)按要求完成下列题目:
(1)解方程组:
(2)已知方程组的解x,y满足,求m的取值范围.
答案解析部分
1.【答案】B
【知识点】不等式的性质
2.【答案】C
【知识点】解一元一次不等式;在数轴上表示不等式的解集
3.【答案】B
【知识点】轴对称图形;中心对称及中心对称图形
4.【答案】C
【知识点】一元一次方程的实际应用-行程问题
5.【答案】D
【知识点】多边形内角与外角;一元一次方程的实际应用-几何问题
6.【答案】D
【知识点】解二元一次方程组;解一元一次不等式;代入消元法解二元一次方程组;加减消元法解二元一次方程组
7.【答案】A
【知识点】三角形全等的判定
8.【答案】D
【知识点】三角形的外角性质;等腰三角形的性质;旋转的性质
9.【答案】A
【知识点】三角形的角平分线、中线和高;三角形的面积;三角形的外角性质;角平分线的概念
10.【答案】C
【知识点】整式的加减运算;一元一次方程的实际应用-几何问题;线段的和、差、倍、分的简单计算
11.【答案】(答案不唯一)
【知识点】三角形全等的判定
12.【答案】
【知识点】列二元一次方程组
13.【答案】
【知识点】列一元一次方程
14.【答案】
【知识点】三角形全等的判定-SAS
15.【答案】
【知识点】多边形内角与外角;圆内接正多边形
16.【答案】-7≤m<-5
【知识点】解一元一次不等式组;一元一次不等式组的应用
17.【答案】解:(1)去分母得,
去括号得,
移项合并同类项得,
系数化为1得,;
在数轴上表示如下:
(2)
解不等式①得,
解不等式②得,
∴不等式组的解集为
【知识点】解一元一次不等式;解一元一次不等式组;在数轴上表示不等式的解集
18.【答案】(1)
(2)
【知识点】解含括号的一元一次方程;解含分数系数的一元一次方程
19.【答案】(1)
(2)226
【知识点】一元一次方程的其他应用;求代数式的值-程序框图
20.【答案】(1)①3;②E;F;③( 3,3)
(2)k的值是1
【知识点】一元一次方程的其他应用;点的坐标;绝对值的概念与意义
21.【答案】(1)
(2)
【知识点】解一元一次方程;解含括号的一元一次方程;解含分数系数的一元一次方程
22.【答案】船在静水中的速度为km/h.
【知识点】一元一次方程的实际应用-行程问题
23.【答案】(1)
(2)或或
(3)或
【知识点】一元一次不等式的应用;一元一次方程的实际应用-几何问题;数轴上两点之间的距离
24.【答案】(1)珍珍第一局的得分为6分;
(2).
【知识点】一元一次方程的实际应用-积分问题
25.【答案】(1)
(2)
【知识点】解二元一次方程组;解一元一次不等式;代入消元法解二元一次方程组
21世纪教育网(www.21cnjy.com)
1 / 8
同课章节目录
