8.4乘法公式（含答案）

中小学教育资源及组卷应用平台
8.4乘法公式
一、单选题
1．下列运算正确的是（　　）
A． B．
C． D．
2．如图，有两个正方形A，B．现将B放在A的内部得图甲，将A，B并列放置后，构造新的正方形得图乙．已知图甲和图乙中阴影部分的面积分别为1和12，若三个正方形A和两个正方形B如图丙摆放，则图丙中阴影部分的面积为（　　）
A．28 B．29 C．30 D．31
3．计算的结果为（　　）
A． B．
C． D．
4．下列运算正确的是（　　）
A． B．
C． D．
5．若a+b＝﹣4，ab＝1，则a2+b2＝（　　）
A．﹣14 B．14 C．7 D．﹣7
二、填空题
6．小林同学把错抄为，抄错后算得的答案为，则正确答案为　 　．
7．如果 ， ，那么 　 　．
8．如图是某校为“五四”晚会搭建的“凹”字型舞台（图中阴影部分），相关数据如图所示，则这个舞台的面积为　 　（用含a，b的代数式表示）．
9．计算：　 　．
10．化简： =　 　．
11．已知，，则的值为　 　．
三、计算题
12．计算： .
13．计算：
（1）（-1）2+ -5-（2004-π）0
（2）[（2x+y）2-y（y+4x）-8x]÷2x．
14．计算：
四、解答题
15．若满足，求的值．
解：设，，则，，
∴．
请仿照上面的方法求解下面问题：
（1）若x满足，求的值；
（2），求；
（3）已知正方形的边长为，，分别是、上的点，且，，长方形的面积是，分别以、为边作正方形，求阴影部分的面积．
五、综合题
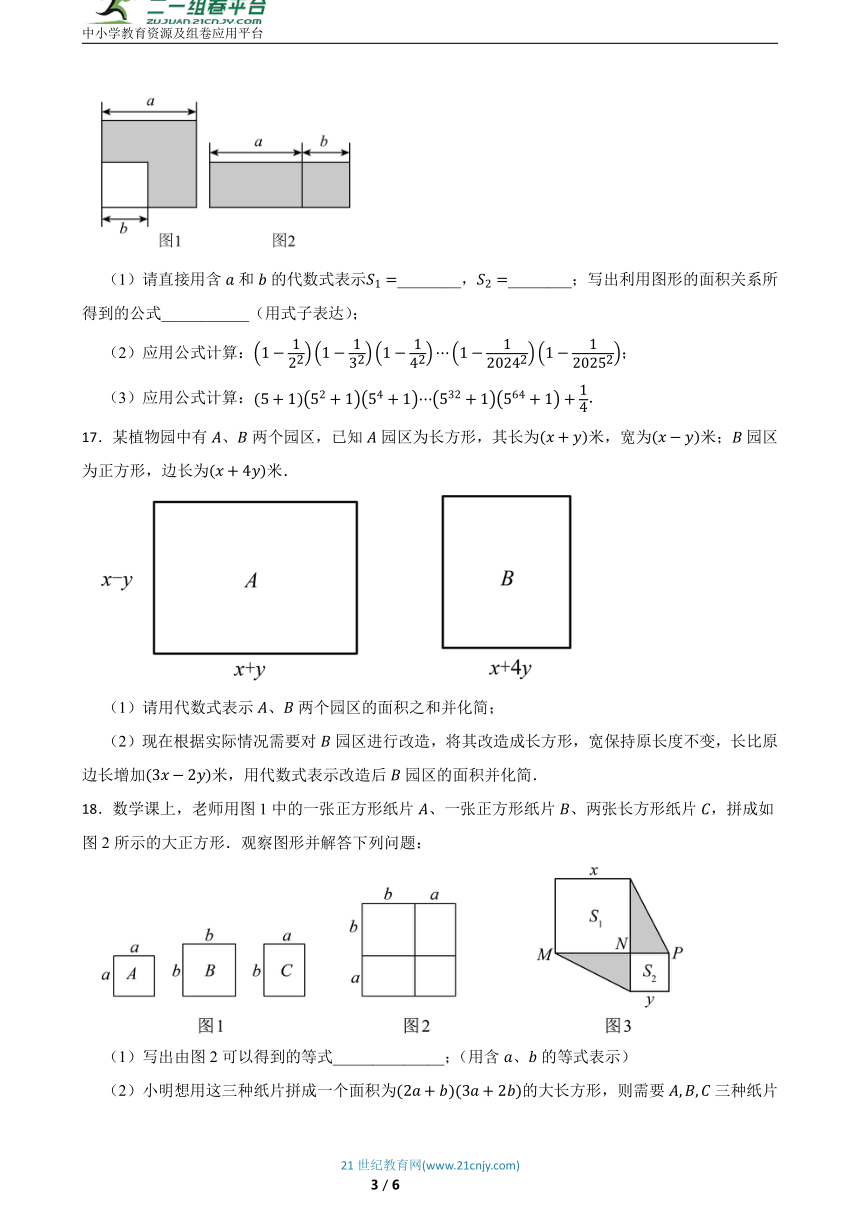
16．如图所示，边长为的正方形中有一个边长为的小正方形，图是由图中阴影部分拼成的一个长方形，设图中阴影部分面积为，图中阴影部分面积为．
（1）请直接用含和的代数式表示________，________；写出利用图形的面积关系所得到的公式___________（用式子表达）；
（2）应用公式计算：；
（3）应用公式计算：．
17．某植物园中有、两个园区，已知园区为长方形，其长为米，宽为米；园区为正方形，边长为米．
（1）请用代数式表示、两个园区的面积之和并化简；
（2）现在根据实际情况需要对园区进行改造，将其改造成长方形，宽保持原长度不变，长比原边长增加米，用代数式表示改造后园区的面积并化简．
18．数学课上，老师用图1中的一张正方形纸片、一张正方形纸片、两张长方形纸片，拼成如图2所示的大正方形．观察图形并解答下列问题：
（1）写出由图2可以得到的等式______________；（用含、的等式表示）
（2）小明想用这三种纸片拼成一个面积为的大长方形，则需要三种纸片各多少张？
（3）如图3，分别表示边长为、的正方形面积，且、、三点在一条直线上，若， ，求图中阴影部分的面积．
六、实践探究题
19．对于一个图形，通过不同的方法计算图形的面积，就可以得到一个数学等式．
（1）模拟练习，如图，写出一个我们熟悉的数学公式；
（2）解决问题：如果，，求的值；
（3）类比探究：如果一个长方形的长和宽分别为和，且，求这个长方形的面积．
答案解析部分
1．【答案】D
【知识点】同底数幂的乘法；完全平方公式及运用；合并同类项法则及应用；幂的乘方运算
2．【答案】B
【知识点】完全平方公式的几何背景；平方差公式的几何背景
3．【答案】A
【知识点】平方差公式及应用
4．【答案】C
【知识点】同底数幂的除法；完全平方公式及运用；合并同类项法则及应用；幂的乘方运算
5．【答案】B
【知识点】完全平方公式及运用
6．【答案】
【知识点】整式的混合运算
7．【答案】3
【知识点】平方差公式及应用
8．【答案】
【知识点】平方差公式及应用；整式的混合运算
9．【答案】
【知识点】完全平方公式及运用
10．【答案】1
【知识点】平方差公式及应用
11．【答案】54
【知识点】完全平方公式及运用
12．【答案】解：原式
【知识点】整式的混合运算
13．【答案】（1）解：原式=1+2-5-1
=-3
（2）解：原式=（4x2+4xy+y2-y2-4xy-8x）÷2x
=（4x2-8x）÷2x
=2x-4．
【知识点】完全平方公式及运用；零指数幂；负整数指数幂
14．【答案】解：
．
【知识点】完全平方公式及运用
15．【答案】（1）
（2）
（3）
【知识点】完全平方公式及运用；完全平方公式的几何背景；平方差公式的几何背景
16．【答案】（1）；；
（2）
（3）
【知识点】平方差公式及应用；平方差公式的几何背景
17．【答案】（1）=平方米
（2）=平方米
【知识点】多项式乘多项式；完全平方公式及运用；整式的混合运算
18．【答案】（1）
（2）需要三种纸片各6张、2张、7张
（3）
【知识点】完全平方公式及运用；完全平方公式的几何背景
19．【答案】（1）；
（2）；
（3）．
【知识点】完全平方公式及运用；完全平方公式的几何背景
21世纪教育网(www.21cnjy.com)
2 / 6