备战2025年高考二轮复习课件 物理(山东版)专题3 电场与磁场 第2讲 磁场 带电粒子在磁场中的运动 课件(40张PPT)
文档属性
| 名称 | 备战2025年高考二轮复习课件 物理(山东版)专题3 电场与磁场 第2讲 磁场 带电粒子在磁场中的运动 课件(40张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-01-13 23:02:53 | ||
图片预览








文档简介
(共40张PPT)
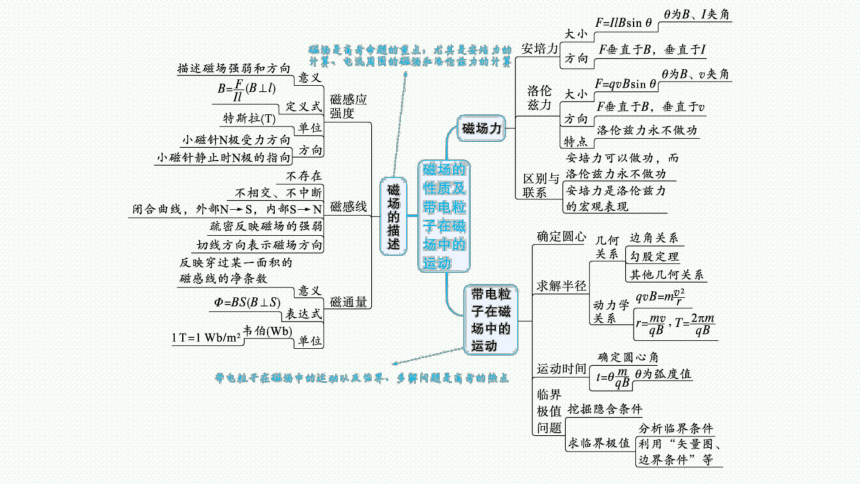
第二讲 磁场 带电粒子在磁场中的运动
通览知识 明要点
研学考点 提能力
目 录 索 引
01
02
突破热点 聚素养
03
通览知识 明要点
研学考点 提能力
考点一 磁场的性质及磁场对电流的作用
高考风向标
考点 考题明细 考查频度
磁场的性质及磁场对电流的作用 2024福建卷,6;2023江苏卷,2; 2022湖北卷,11;2022湖南卷,3; 2022浙江1月选考,3 地方卷:
3年5考
命题角度1 磁场的叠加
(1)根据安培定则确定通电导线周围磁场的方向。
即磁感应强度的方向
(2)磁场中某点磁感应强度的方向为该点磁感线的切线方向。
(3)磁感应强度是矢量,多个通电导体产生的磁场叠加时,合磁场的磁感应强度等于通电导体分别单独存在时在该点磁感应强度的矢量和。
用平行四边形定则或三角形定则
例1 (多选)(2024浙江绍兴期末)两完全相同的通电圆线圈1、2平行放置,两圆线圈的圆心O1、O2的连线与圆面垂直,O为O1、O2的连线的中点,如图所示。当两圆线圈中通以方向、大小均相同的恒定电流时,O1点的磁感应强度的大小为B1;若保持线圈1中的电流以及线圈2中的电流大小不变,仅将线圈2中电流方向反向,O1点的磁感应强度的大小为B2。线圈1中的电流在O2点和O点产生的磁感应强度大小分别为B3、B4,
则下列关系中一定正确的有( )
BD
解析 当两圆环中电流方向相同时,设两圆环在O1点产生的磁场大小分别为B11和B21,则O1点的磁感应强度的大小为B1=B11+B21,仅将线圈2中电流方向反向,则此时O1点的磁感应强度的大小为B2=B11-B21,联立解得
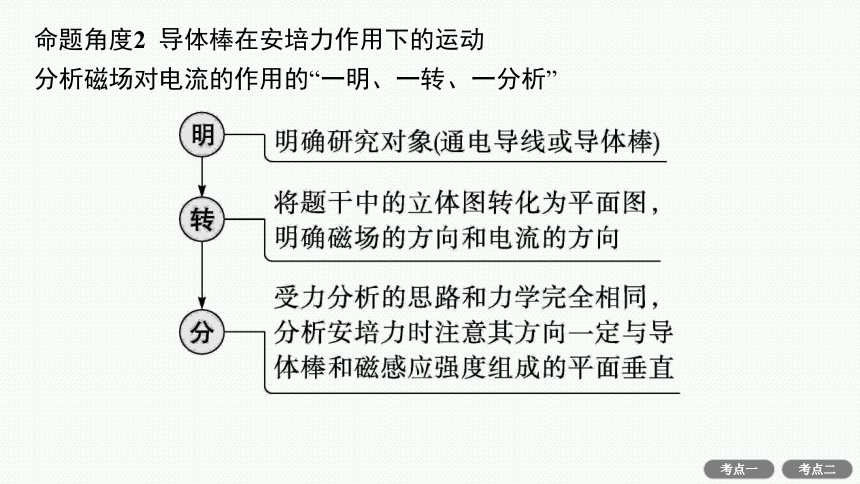
命题角度2 导体棒在安培力作用下的运动
分析磁场对电流的作用的“一明、一转、一分析”
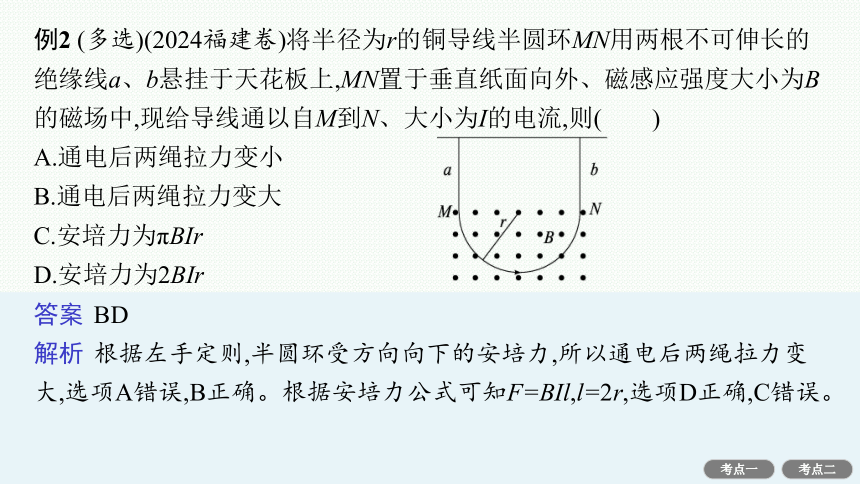
例2 (多选)(2024福建卷)将半径为r的铜导线半圆环MN用两根不可伸长的绝缘线a、b悬挂于天花板上,MN置于垂直纸面向外、磁感应强度大小为B的磁场中,现给导线通以自M到N、大小为I的电流,则( )
A.通电后两绳拉力变小
B.通电后两绳拉力变大
C.安培力为πBIr
D.安培力为2BIr
答案 BD
解析 根据左手定则,半圆环受方向向下的安培力,所以通电后两绳拉力变大,选项A错误,B正确。根据安培力公式可知F=BIl,l=2r,选项D正确,C错误。
拓展衍生
1.(多选)(2024海南海口期中)如图所示是一种含有电磁铁的电磁泵,C形铁芯由硅钢片叠成,铁芯右侧绕有线圈,左侧开口中嵌入输送导电液体的管道,管道两侧有电极。管道内的导电液体和线圈连通,与电源构成导电回路。通电后,电磁泵驱使管道内液体从纸面内持续流向纸面外,或从纸面外持续流向纸面内,下列说法正确的是( )
A.当a端接直流电源正极时,液体向纸面内方向持续流动
B.当b端接直流电源正极时,液体向纸面外方向持续流动
C.当a、b端接交流电源时,液体不可能单方向持续流动
D.当a、b端接交流电源时,液体可以向纸面内单方向
持续流动
AD
解析 当a端接直流电源正极时,管道内导电液体中电流方向从左到右,根据安培定则,管道内导电液体中磁场方向由上到下,再根据左手定则,可判断受力方向指向纸面内,同理可得,当b端接直流电源正极时,液体向纸面内方向持续流动,故A正确,B错误;当a、b端接交流电源时,设电路接通瞬间a端为正极,则管道内导电液体受力方向指向纸面内,当a端变成负极之后,磁场方向也变了,受力方向依然指向纸面内,液体受力方向与电源极性变化无关,液体可以向纸面内单方向持续流动,故C错误,D正确。故选A、D。
考点二 带电粒子在匀强磁场中的运动
高考风向标
考点 考题明细 考查频度
带电粒子在磁场中的运动 2024广西卷,5;2024河北卷,10; 2023全国乙卷,18;2023全国甲卷,20; 2023湖北卷,15;2022辽宁卷,8; 2022广东卷,7;2022湖北卷,8 全国卷:
3年2考
地方卷:
3年6考
命题角度1 带电粒子在有界磁场中的运动
1.基本规律
2.轨迹圆的几个基本特点
(1)带电粒子从同一直线边界射入和射出匀强磁场时,入射角等于出射角,如图甲所示,θ3=θ2=θ1。
(2)带电粒子经过匀强磁场时速度方向的偏转角等于其轨迹的圆心角,如图甲所示,α1=α2。
(3)沿半径方向射入圆形匀强磁场的粒子,出射时亦沿半径方向,如图乙所示,粒子在磁场中的运动轨迹关于连线OO'对称。
3.半径确定的两种方法
方法二:由几何关系求。一般由数学知识(勾股定理、三角函数等)通过计算来确定。
4.时间确定的两种方法
例3 (2024广西卷)Oxy坐标平面内一有界匀强磁场区域如图所示,磁感应强度大小为B,方向垂直于纸面向里。质量为m、电荷量为+q的粒子,以初速度v从O点沿x轴正向开始运动,粒子过y轴时速度方向与y轴正向夹角为45°,交点为P。不计粒子重力,则P点至O点的距离为( )
C
命题角度2 带电粒子在磁场中的临界极值问题
两种思路 一是以定理、定律为依据,首先求出所研究问题的一般规律和一般解的形式,然后分析、讨论处于临界条件时的特殊规律和特殊解
二是直接分析、讨论临界状态,找出临界条件,从而通过临界条件求出临界值
两种方法 物理 方法 (1)利用临界条件求极值;(2)利用边界条件求极值;(3)利用矢量图求极值
数学 方法 (1)用三角函数求极值;(2)用一元二次方程的判别式求极值;
(3)用不等式的性质求极值;(4)用图像法求极值
四个 结论 (1)刚好穿出磁场边界的条件是带电粒子在磁场中运动的轨迹与边界相切。
(2)当速率v一定时,弧长(或圆心角小于180°时的弦长)越长,圆心角越大,则带电粒子在有界磁场中运动的时间越长。
(3)当速率v变化时,圆心角越大,运动时间越长。
(4)在圆形匀强磁场中,若带电粒子速率v一定且运动轨迹圆半径大于磁场区域圆半径,则入射点和出射点为磁场直径的两个端点时,轨迹对应的偏转角最大(所有的弦长中直径最长)
例4 (2024贵州遵义三模)如图所示,空间存在垂直纸面向外的环形匀强磁场,磁感应强度为B,磁场内外边界为两个同心圆,半径分别为R、3R。现有质量为m、电荷量为q的粒子,沿半径方向垂直于磁场进入环形区域,粒子恰好不能进入小圆区域,不计重力。则粒子在磁场中运动的( )
A.轨道半径为1.5R
B.轨道半径为3R
答案 C
解析 设粒子带正电,粒子恰好不能进入小圆区域,轨迹如图所示。
根据几何关系可得r2+(3R)2=(r+R)2,解得粒子轨道半径为r=4R,
故A、B错误;
拓展衍生
量为m,电荷量为q),其速度方向均垂直于磁场方向,与OP的夹角分别为90°、60°,不计粒子的重力及粒子间相互作用,则两个粒子a、b在磁场中的运动时间之比ta∶tb为( )
A.1∶1
B.2∶1
C.1∶2
D.4∶1
A
解析 两个粒子在磁场中做圆周运动的半径均为R,恰好与磁场区域半径相等。如图甲所示,对a粒子,在磁场中恰好以P点为圆心做圆周运动,从圆弧AP上的M点出磁场,由几何关系得∠OPM=60°,则ta= T;如图乙所示,对b粒子,在磁场中做圆周运动恰好从圆弧AP上的D点出磁场,由几何关系得∠OO'D=60°,则tb= T,故ta∶tb=1∶1,故A正确,B、C、D错误。
3.(多选)(2024河北卷)如图所示,真空区域有同心正方形ABCD和abcd,其各对应边平行,ABCD的边长一定,abcd的边长可调,两正方形之间充满恒定匀强磁场,方向垂直于正方形所在平面。A处有一个粒子源,可逐个发射速度不等、比荷相等的粒子,粒子沿AD方向进入磁场。调整abcd的边长,可使速度大小合适的粒子经ad边穿过无磁场区后由BC边射出。
对满足前述条件的粒子,下列说法正确的是( )
A.若粒子穿过ad边时速度方向与ad边夹角为45°,则粒子必垂直于BC射出
B.若粒子穿过ad边时速度方向与ad边夹角为60°,则粒子必垂直于BC射出
C.若粒子经cd边垂直于BC射出,则粒子穿过ad边的速度方向与ad边夹角必为45°
D.若粒子经bc边垂直于BC射出,则粒子穿过ad边时速度方向与ad边夹角必为60°
答案 AD
解析 若粒子穿过ad边时速度方向与ad边夹角为45°,则粒子必经过cd边,作出粒子运动轨迹图,如图甲所示,粒子从C点垂直于BC射出,故A正确。进一步分析可知,若粒子经cd边垂直于BC射出,但不过C点时,粒子穿过ad边的速度方向与ad边夹角不为45°,故C错误。粒子穿过ad边时速度方向与ad边夹角为60°时,若粒子从cd边(除c点外)再次进入磁场,作出粒子运动轨迹如图乙所示,则粒子不可能垂直于BC射出;若粒子从bc边再次进入磁场,作出粒子运动轨迹如图丙所示,则粒子一定垂直于BC射出,故B错误,D正确。
甲
乙
丙
突破热点 聚素养
模型建构
经典物理模型:常见的动态圆模型
1.粒子射出或不射出磁场的临界状态是粒子运动轨迹与磁场边界相切。
2.常见的动态圆
模型 示意图 适用条件 应用方法
放 缩 圆 轨迹圆的圆心在直线PP2上 粒子的入射点位置相同,速度方向一定,速度大小不同 以入射点P为定点,将半径放缩作轨迹圆,粒子恰好不射出磁场的临界状态是粒子运动轨迹与磁场边界相切
模型 示意图 适用条件 应用方法
磁聚焦与磁发散 磁聚焦 磁发散 粒子速度大小相同,轨迹圆半径等于磁场区域圆半径 带电粒子平行射入圆形有界匀强磁场,则粒子从磁场边界上同一点射出,该点切线与入射方向平行——磁聚焦;带电粒子从磁场边缘某点以不同方向入射时,将从磁场区域平行出射——磁发散
考向分析
带电粒子在磁场中的运动历来是高考的热点问题,高考对该部分的考查以带电粒子在各种有界磁场中的运动为主,通常涉及临界极值问题,对考生利用数学知识解决物理问题的能力要求较高。解决带电粒子在匀强磁场中运动的临界问题,关键在于运用动态思维,利用动态圆思想寻找临界点,确定临界状态,根据粒子的速度方向找出半径方向,同时由磁场边界和题设条件画好轨迹,定好圆心,建立几何关系。
案例探究
典例 (多选)如图所示,边长为2L的等边三角形ABC内有垂直纸面向里、磁感应强度大小为B0的匀强磁场,D是AB边的中点,一质量为m、电荷量为-q的带电粒子从D点以不同的速率沿平行于BC边方向射入磁场,不计粒子重力,下列说法正确的是( )
A.粒子可能从B点射出
D.若粒子从AB边射出,则粒子在磁场中运动的时间相同,且时间最长
答案 CD
解析 带负电的粒子从D点以速度v沿平行于BC边方向射入磁场。由左手定则可知,粒子向下偏转,但根据几何知识,由于BC边的限制,粒子不能到达B点,故A错误;若粒子从C点射出,如图甲所示,设此时粒子的轨迹半径为R2,
甲
乙
角度拓展
(2024重庆模拟调研)如图所示,半径为R的圆形区域的圆心位于直角坐标系的坐标原点O,该圆形区域内有垂直坐标平面的匀强磁场(图中未画出)。磁场区域外右侧有宽度为R的粒子源,M、N为粒子源两端点,M、N连线垂直于x轴,粒子源中点P位于x轴上,粒子源持续向x轴负方向发射质量为m、电荷量为q(q>0)、速率为v的粒子。已知从粒子源中点P发出的粒子,经过磁场区域后,恰能从圆与y轴负半轴的交点Q处沿y轴负方向射出磁场,不计粒子重力及粒子间相互作用力。求:
(1)匀强磁场的磁感应强度;
(2)从粒子源发出的粒子经过磁场
区域的路程s的范围。
解析 (1)根据题意可知从粒子源中点P发出的粒子在磁场中运动轨迹为四分之一圆周,轨迹半径为r1,由几何关系可知r1=R
甲
根据题意可知,从M点射出的粒子在磁场中运动的路程最长,如图乙所示
易知四边形O2DOQ为菱形,根据几何关系可知∠QO2D=120°
乙
第二讲 磁场 带电粒子在磁场中的运动
通览知识 明要点
研学考点 提能力
目 录 索 引
01
02
突破热点 聚素养
03
通览知识 明要点
研学考点 提能力
考点一 磁场的性质及磁场对电流的作用
高考风向标
考点 考题明细 考查频度
磁场的性质及磁场对电流的作用 2024福建卷,6;2023江苏卷,2; 2022湖北卷,11;2022湖南卷,3; 2022浙江1月选考,3 地方卷:
3年5考
命题角度1 磁场的叠加
(1)根据安培定则确定通电导线周围磁场的方向。
即磁感应强度的方向
(2)磁场中某点磁感应强度的方向为该点磁感线的切线方向。
(3)磁感应强度是矢量,多个通电导体产生的磁场叠加时,合磁场的磁感应强度等于通电导体分别单独存在时在该点磁感应强度的矢量和。
用平行四边形定则或三角形定则
例1 (多选)(2024浙江绍兴期末)两完全相同的通电圆线圈1、2平行放置,两圆线圈的圆心O1、O2的连线与圆面垂直,O为O1、O2的连线的中点,如图所示。当两圆线圈中通以方向、大小均相同的恒定电流时,O1点的磁感应强度的大小为B1;若保持线圈1中的电流以及线圈2中的电流大小不变,仅将线圈2中电流方向反向,O1点的磁感应强度的大小为B2。线圈1中的电流在O2点和O点产生的磁感应强度大小分别为B3、B4,
则下列关系中一定正确的有( )
BD
解析 当两圆环中电流方向相同时,设两圆环在O1点产生的磁场大小分别为B11和B21,则O1点的磁感应强度的大小为B1=B11+B21,仅将线圈2中电流方向反向,则此时O1点的磁感应强度的大小为B2=B11-B21,联立解得
命题角度2 导体棒在安培力作用下的运动
分析磁场对电流的作用的“一明、一转、一分析”
例2 (多选)(2024福建卷)将半径为r的铜导线半圆环MN用两根不可伸长的绝缘线a、b悬挂于天花板上,MN置于垂直纸面向外、磁感应强度大小为B的磁场中,现给导线通以自M到N、大小为I的电流,则( )
A.通电后两绳拉力变小
B.通电后两绳拉力变大
C.安培力为πBIr
D.安培力为2BIr
答案 BD
解析 根据左手定则,半圆环受方向向下的安培力,所以通电后两绳拉力变大,选项A错误,B正确。根据安培力公式可知F=BIl,l=2r,选项D正确,C错误。
拓展衍生
1.(多选)(2024海南海口期中)如图所示是一种含有电磁铁的电磁泵,C形铁芯由硅钢片叠成,铁芯右侧绕有线圈,左侧开口中嵌入输送导电液体的管道,管道两侧有电极。管道内的导电液体和线圈连通,与电源构成导电回路。通电后,电磁泵驱使管道内液体从纸面内持续流向纸面外,或从纸面外持续流向纸面内,下列说法正确的是( )
A.当a端接直流电源正极时,液体向纸面内方向持续流动
B.当b端接直流电源正极时,液体向纸面外方向持续流动
C.当a、b端接交流电源时,液体不可能单方向持续流动
D.当a、b端接交流电源时,液体可以向纸面内单方向
持续流动
AD
解析 当a端接直流电源正极时,管道内导电液体中电流方向从左到右,根据安培定则,管道内导电液体中磁场方向由上到下,再根据左手定则,可判断受力方向指向纸面内,同理可得,当b端接直流电源正极时,液体向纸面内方向持续流动,故A正确,B错误;当a、b端接交流电源时,设电路接通瞬间a端为正极,则管道内导电液体受力方向指向纸面内,当a端变成负极之后,磁场方向也变了,受力方向依然指向纸面内,液体受力方向与电源极性变化无关,液体可以向纸面内单方向持续流动,故C错误,D正确。故选A、D。
考点二 带电粒子在匀强磁场中的运动
高考风向标
考点 考题明细 考查频度
带电粒子在磁场中的运动 2024广西卷,5;2024河北卷,10; 2023全国乙卷,18;2023全国甲卷,20; 2023湖北卷,15;2022辽宁卷,8; 2022广东卷,7;2022湖北卷,8 全国卷:
3年2考
地方卷:
3年6考
命题角度1 带电粒子在有界磁场中的运动
1.基本规律
2.轨迹圆的几个基本特点
(1)带电粒子从同一直线边界射入和射出匀强磁场时,入射角等于出射角,如图甲所示,θ3=θ2=θ1。
(2)带电粒子经过匀强磁场时速度方向的偏转角等于其轨迹的圆心角,如图甲所示,α1=α2。
(3)沿半径方向射入圆形匀强磁场的粒子,出射时亦沿半径方向,如图乙所示,粒子在磁场中的运动轨迹关于连线OO'对称。
3.半径确定的两种方法
方法二:由几何关系求。一般由数学知识(勾股定理、三角函数等)通过计算来确定。
4.时间确定的两种方法
例3 (2024广西卷)Oxy坐标平面内一有界匀强磁场区域如图所示,磁感应强度大小为B,方向垂直于纸面向里。质量为m、电荷量为+q的粒子,以初速度v从O点沿x轴正向开始运动,粒子过y轴时速度方向与y轴正向夹角为45°,交点为P。不计粒子重力,则P点至O点的距离为( )
C
命题角度2 带电粒子在磁场中的临界极值问题
两种思路 一是以定理、定律为依据,首先求出所研究问题的一般规律和一般解的形式,然后分析、讨论处于临界条件时的特殊规律和特殊解
二是直接分析、讨论临界状态,找出临界条件,从而通过临界条件求出临界值
两种方法 物理 方法 (1)利用临界条件求极值;(2)利用边界条件求极值;(3)利用矢量图求极值
数学 方法 (1)用三角函数求极值;(2)用一元二次方程的判别式求极值;
(3)用不等式的性质求极值;(4)用图像法求极值
四个 结论 (1)刚好穿出磁场边界的条件是带电粒子在磁场中运动的轨迹与边界相切。
(2)当速率v一定时,弧长(或圆心角小于180°时的弦长)越长,圆心角越大,则带电粒子在有界磁场中运动的时间越长。
(3)当速率v变化时,圆心角越大,运动时间越长。
(4)在圆形匀强磁场中,若带电粒子速率v一定且运动轨迹圆半径大于磁场区域圆半径,则入射点和出射点为磁场直径的两个端点时,轨迹对应的偏转角最大(所有的弦长中直径最长)
例4 (2024贵州遵义三模)如图所示,空间存在垂直纸面向外的环形匀强磁场,磁感应强度为B,磁场内外边界为两个同心圆,半径分别为R、3R。现有质量为m、电荷量为q的粒子,沿半径方向垂直于磁场进入环形区域,粒子恰好不能进入小圆区域,不计重力。则粒子在磁场中运动的( )
A.轨道半径为1.5R
B.轨道半径为3R
答案 C
解析 设粒子带正电,粒子恰好不能进入小圆区域,轨迹如图所示。
根据几何关系可得r2+(3R)2=(r+R)2,解得粒子轨道半径为r=4R,
故A、B错误;
拓展衍生
量为m,电荷量为q),其速度方向均垂直于磁场方向,与OP的夹角分别为90°、60°,不计粒子的重力及粒子间相互作用,则两个粒子a、b在磁场中的运动时间之比ta∶tb为( )
A.1∶1
B.2∶1
C.1∶2
D.4∶1
A
解析 两个粒子在磁场中做圆周运动的半径均为R,恰好与磁场区域半径相等。如图甲所示,对a粒子,在磁场中恰好以P点为圆心做圆周运动,从圆弧AP上的M点出磁场,由几何关系得∠OPM=60°,则ta= T;如图乙所示,对b粒子,在磁场中做圆周运动恰好从圆弧AP上的D点出磁场,由几何关系得∠OO'D=60°,则tb= T,故ta∶tb=1∶1,故A正确,B、C、D错误。
3.(多选)(2024河北卷)如图所示,真空区域有同心正方形ABCD和abcd,其各对应边平行,ABCD的边长一定,abcd的边长可调,两正方形之间充满恒定匀强磁场,方向垂直于正方形所在平面。A处有一个粒子源,可逐个发射速度不等、比荷相等的粒子,粒子沿AD方向进入磁场。调整abcd的边长,可使速度大小合适的粒子经ad边穿过无磁场区后由BC边射出。
对满足前述条件的粒子,下列说法正确的是( )
A.若粒子穿过ad边时速度方向与ad边夹角为45°,则粒子必垂直于BC射出
B.若粒子穿过ad边时速度方向与ad边夹角为60°,则粒子必垂直于BC射出
C.若粒子经cd边垂直于BC射出,则粒子穿过ad边的速度方向与ad边夹角必为45°
D.若粒子经bc边垂直于BC射出,则粒子穿过ad边时速度方向与ad边夹角必为60°
答案 AD
解析 若粒子穿过ad边时速度方向与ad边夹角为45°,则粒子必经过cd边,作出粒子运动轨迹图,如图甲所示,粒子从C点垂直于BC射出,故A正确。进一步分析可知,若粒子经cd边垂直于BC射出,但不过C点时,粒子穿过ad边的速度方向与ad边夹角不为45°,故C错误。粒子穿过ad边时速度方向与ad边夹角为60°时,若粒子从cd边(除c点外)再次进入磁场,作出粒子运动轨迹如图乙所示,则粒子不可能垂直于BC射出;若粒子从bc边再次进入磁场,作出粒子运动轨迹如图丙所示,则粒子一定垂直于BC射出,故B错误,D正确。
甲
乙
丙
突破热点 聚素养
模型建构
经典物理模型:常见的动态圆模型
1.粒子射出或不射出磁场的临界状态是粒子运动轨迹与磁场边界相切。
2.常见的动态圆
模型 示意图 适用条件 应用方法
放 缩 圆 轨迹圆的圆心在直线PP2上 粒子的入射点位置相同,速度方向一定,速度大小不同 以入射点P为定点,将半径放缩作轨迹圆,粒子恰好不射出磁场的临界状态是粒子运动轨迹与磁场边界相切
模型 示意图 适用条件 应用方法
磁聚焦与磁发散 磁聚焦 磁发散 粒子速度大小相同,轨迹圆半径等于磁场区域圆半径 带电粒子平行射入圆形有界匀强磁场,则粒子从磁场边界上同一点射出,该点切线与入射方向平行——磁聚焦;带电粒子从磁场边缘某点以不同方向入射时,将从磁场区域平行出射——磁发散
考向分析
带电粒子在磁场中的运动历来是高考的热点问题,高考对该部分的考查以带电粒子在各种有界磁场中的运动为主,通常涉及临界极值问题,对考生利用数学知识解决物理问题的能力要求较高。解决带电粒子在匀强磁场中运动的临界问题,关键在于运用动态思维,利用动态圆思想寻找临界点,确定临界状态,根据粒子的速度方向找出半径方向,同时由磁场边界和题设条件画好轨迹,定好圆心,建立几何关系。
案例探究
典例 (多选)如图所示,边长为2L的等边三角形ABC内有垂直纸面向里、磁感应强度大小为B0的匀强磁场,D是AB边的中点,一质量为m、电荷量为-q的带电粒子从D点以不同的速率沿平行于BC边方向射入磁场,不计粒子重力,下列说法正确的是( )
A.粒子可能从B点射出
D.若粒子从AB边射出,则粒子在磁场中运动的时间相同,且时间最长
答案 CD
解析 带负电的粒子从D点以速度v沿平行于BC边方向射入磁场。由左手定则可知,粒子向下偏转,但根据几何知识,由于BC边的限制,粒子不能到达B点,故A错误;若粒子从C点射出,如图甲所示,设此时粒子的轨迹半径为R2,
甲
乙
角度拓展
(2024重庆模拟调研)如图所示,半径为R的圆形区域的圆心位于直角坐标系的坐标原点O,该圆形区域内有垂直坐标平面的匀强磁场(图中未画出)。磁场区域外右侧有宽度为R的粒子源,M、N为粒子源两端点,M、N连线垂直于x轴,粒子源中点P位于x轴上,粒子源持续向x轴负方向发射质量为m、电荷量为q(q>0)、速率为v的粒子。已知从粒子源中点P发出的粒子,经过磁场区域后,恰能从圆与y轴负半轴的交点Q处沿y轴负方向射出磁场,不计粒子重力及粒子间相互作用力。求:
(1)匀强磁场的磁感应强度;
(2)从粒子源发出的粒子经过磁场
区域的路程s的范围。
解析 (1)根据题意可知从粒子源中点P发出的粒子在磁场中运动轨迹为四分之一圆周,轨迹半径为r1,由几何关系可知r1=R
甲
根据题意可知,从M点射出的粒子在磁场中运动的路程最长,如图乙所示
易知四边形O2DOQ为菱形,根据几何关系可知∠QO2D=120°
乙
同课章节目录
