人教B版 选择性必修第一册 2.5.1 椭圆的标准方程 课件(共16张PPT)
文档属性
| 名称 | 人教B版 选择性必修第一册 2.5.1 椭圆的标准方程 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 10.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-13 00:00:00 | ||
图片预览




文档简介
2.5.1 椭圆的标准方程
追根溯源:圆锥曲线的形成
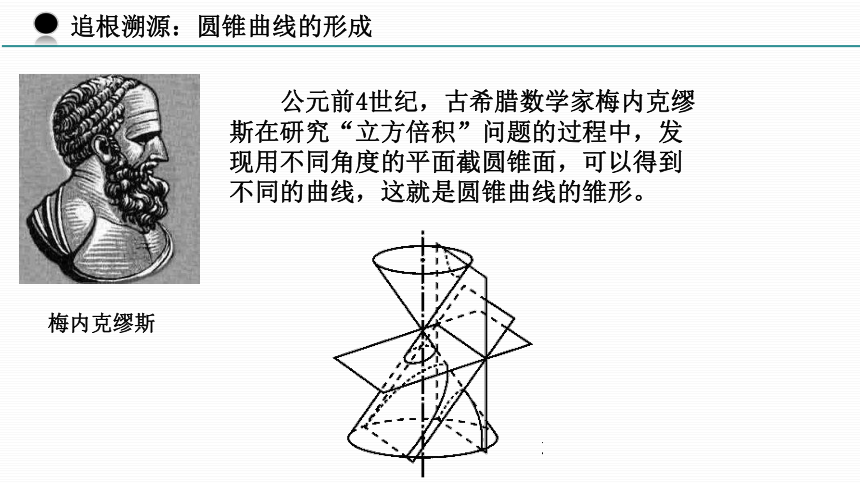
公元前4世纪,古希腊数学家梅内克缪斯在研究“立方倍积”问题的过程中,发现用不同角度的平面截圆锥面,可以得到不同的曲线,这就是圆锥曲线的雏形。
梅内克缪斯
追根溯源:圆锥曲线的形成
追根溯源:圆锥曲线的形成
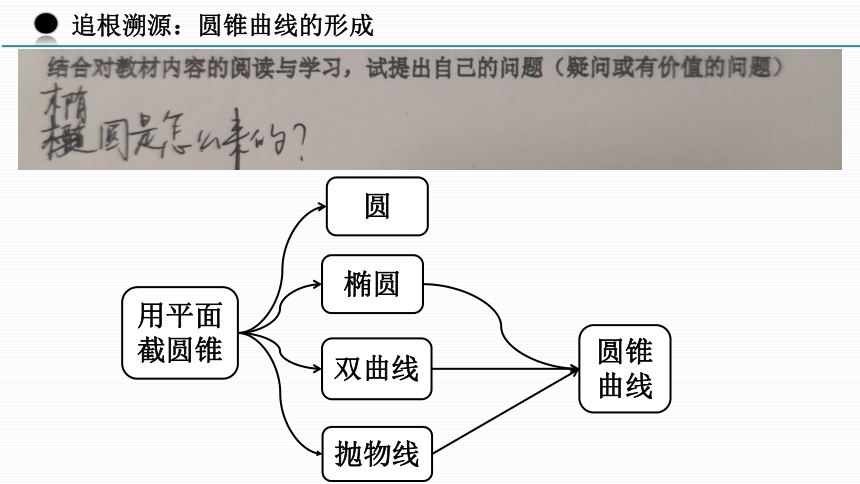
用平面截圆锥
抛物线
双曲线
椭圆
圆锥曲线
圆
阿波罗尼奥斯
大约在公元前200年,古希腊数学家阿波罗尼奥斯在著作《圆锥曲线论》中以纯几何的方法将圆锥曲线的性质网罗殆尽,几乎使后人没有插足的余地.
追根溯源:圆锥曲线的历史
《圆锥曲线论》与欧几里得的《几何原本》同被誉为古希腊几何登峰造极之作.
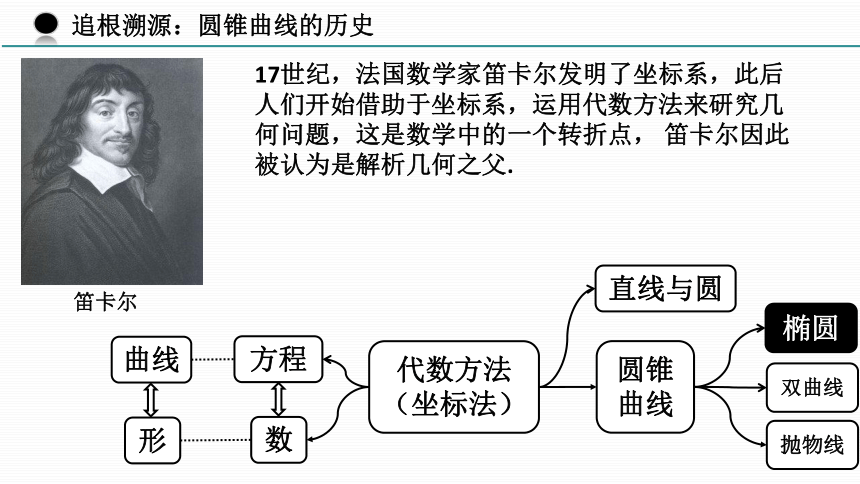
笛卡尔
17世纪,法国数学家笛卡尔发明了坐标系,此后人们开始借助于坐标系,运用代数方法来研究几何问题,这是数学中的一个转折点, 笛卡尔因此被认为是解析几何之父.
追根溯源:圆锥曲线的历史
圆锥曲线
抛物线
双曲线
椭圆
直线与圆
曲线
方程
代数方法
(坐标法)
数
形
Germinal Pierre Dandelin
比利时数学家
19世纪初,比利时数学家旦德林用与圆锥面和截面均相切的两个球(Dandelin双球),发现了椭圆的几何特性.
概念探究:椭圆的定义
问题一:椭圆上的点具有怎样的几何特性?
请动手试验!
概念探究:椭圆的定义
是否满足到两个定点距离之和等于常数的点的轨迹就是椭圆?
动点轨迹不存在
绳长大于两定点之间的距离:
绳长等于两定点之间的距离:
动点轨迹是线段
绳长小于两定点之间的距离:
平面内与两个定点F1,F2的距离的和等于常数(大于|F1F2 |)的点的轨迹叫椭圆. 这两个定点F1,F2叫做椭圆的焦点. 两焦点之间的距离叫做焦距,焦距的一半称为半焦距.
记为2a
概念探究:椭圆的定义
自然语言
数学语言
记为2c
问题二:椭圆的方程如何推导?
求曲线方程的一般步骤:
方程探究:椭圆标准方程
方程探究:椭圆标准方程
椭圆第二定义
椭圆的定义与方程
第二定义
标准方程
焦点在y轴
焦点在x轴
定义
平面截圆锥
椭圆
?
求椭圆标准方程的规律方法
1.求椭圆的标准方程时,要“先定型,再定量”.
2.定 义 法:求出a和c,进一步求出b.
待定系数法:先设出标准方程,根据两个条件联立方程组,
直接求出a,b.
总结归纳
用平面截圆锥
抛物线
定义
性质
方程
双曲线
椭圆
总结升华
数学
抽象
数学
运算
应用
直
观
想
象
几何问题代数化(数形结合)
巩固作业:
课本P109练习1,2,3,4
探究作业:
1. 探究椭圆是否还有其它画法,并研究画法的理论基础。
2. 探究椭圆标准方程是否还有其它推导方法?
3. 思考:
课后延伸
只要代数和几何沿着各自的途径去发展,它们的进展将是缓慢的,他们的应用也是很有限的。但是,当这两门学科结成伴侣,它们都将从对方身上获得新鲜的活力,因此,以快速的步伐猛进,趋于完美。
——拉格朗日
追根溯源:圆锥曲线的形成
公元前4世纪,古希腊数学家梅内克缪斯在研究“立方倍积”问题的过程中,发现用不同角度的平面截圆锥面,可以得到不同的曲线,这就是圆锥曲线的雏形。
梅内克缪斯
追根溯源:圆锥曲线的形成
追根溯源:圆锥曲线的形成
用平面截圆锥
抛物线
双曲线
椭圆
圆锥曲线
圆
阿波罗尼奥斯
大约在公元前200年,古希腊数学家阿波罗尼奥斯在著作《圆锥曲线论》中以纯几何的方法将圆锥曲线的性质网罗殆尽,几乎使后人没有插足的余地.
追根溯源:圆锥曲线的历史
《圆锥曲线论》与欧几里得的《几何原本》同被誉为古希腊几何登峰造极之作.
笛卡尔
17世纪,法国数学家笛卡尔发明了坐标系,此后人们开始借助于坐标系,运用代数方法来研究几何问题,这是数学中的一个转折点, 笛卡尔因此被认为是解析几何之父.
追根溯源:圆锥曲线的历史
圆锥曲线
抛物线
双曲线
椭圆
直线与圆
曲线
方程
代数方法
(坐标法)
数
形
Germinal Pierre Dandelin
比利时数学家
19世纪初,比利时数学家旦德林用与圆锥面和截面均相切的两个球(Dandelin双球),发现了椭圆的几何特性.
概念探究:椭圆的定义
问题一:椭圆上的点具有怎样的几何特性?
请动手试验!
概念探究:椭圆的定义
是否满足到两个定点距离之和等于常数的点的轨迹就是椭圆?
动点轨迹不存在
绳长大于两定点之间的距离:
绳长等于两定点之间的距离:
动点轨迹是线段
绳长小于两定点之间的距离:
平面内与两个定点F1,F2的距离的和等于常数(大于|F1F2 |)的点的轨迹叫椭圆. 这两个定点F1,F2叫做椭圆的焦点. 两焦点之间的距离叫做焦距,焦距的一半称为半焦距.
记为2a
概念探究:椭圆的定义
自然语言
数学语言
记为2c
问题二:椭圆的方程如何推导?
求曲线方程的一般步骤:
方程探究:椭圆标准方程
方程探究:椭圆标准方程
椭圆第二定义
椭圆的定义与方程
第二定义
标准方程
焦点在y轴
焦点在x轴
定义
平面截圆锥
椭圆
?
求椭圆标准方程的规律方法
1.求椭圆的标准方程时,要“先定型,再定量”.
2.定 义 法:求出a和c,进一步求出b.
待定系数法:先设出标准方程,根据两个条件联立方程组,
直接求出a,b.
总结归纳
用平面截圆锥
抛物线
定义
性质
方程
双曲线
椭圆
总结升华
数学
抽象
数学
运算
应用
直
观
想
象
几何问题代数化(数形结合)
巩固作业:
课本P109练习1,2,3,4
探究作业:
1. 探究椭圆是否还有其它画法,并研究画法的理论基础。
2. 探究椭圆标准方程是否还有其它推导方法?
3. 思考:
课后延伸
只要代数和几何沿着各自的途径去发展,它们的进展将是缓慢的,他们的应用也是很有限的。但是,当这两门学科结成伴侣,它们都将从对方身上获得新鲜的活力,因此,以快速的步伐猛进,趋于完美。
——拉格朗日
