7.2.2 平行线的判定 课件(共19张PPT) 2024-2025学年人教版数学七年级下册
文档属性
| 名称 | 7.2.2 平行线的判定 课件(共19张PPT) 2024-2025学年人教版数学七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 753.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-15 13:02:49 | ||
图片预览





文档简介
(共19张PPT)
7.2平行线
7.2.2平行线的判定
掌握两条直线平行的方法,能运用平行线的判定方法进行简单的推理论证.
通过对两条直线平行条件的探索,理解两直线平行的条件.
感受数学来源于生活,激发学生学习数学的兴趣,培养学生的逻辑思维能力.
1
2
3
【重点】理解并掌握两条直线平行的方法.
【难点】理解由判定方法一推出判定方法二,三的证明过程.
在同一平面内,如果两条直线不相交的叫做_______.
平行线
【问题1】但由于直线是无限延伸的,检验它们是否相交有困难,难以直接判断,那么有没有其他判定方法呢?
b
a
一放
观察右边的动画,你能发现什么?
【探究】
a
b
二靠
四画
三推
a
b
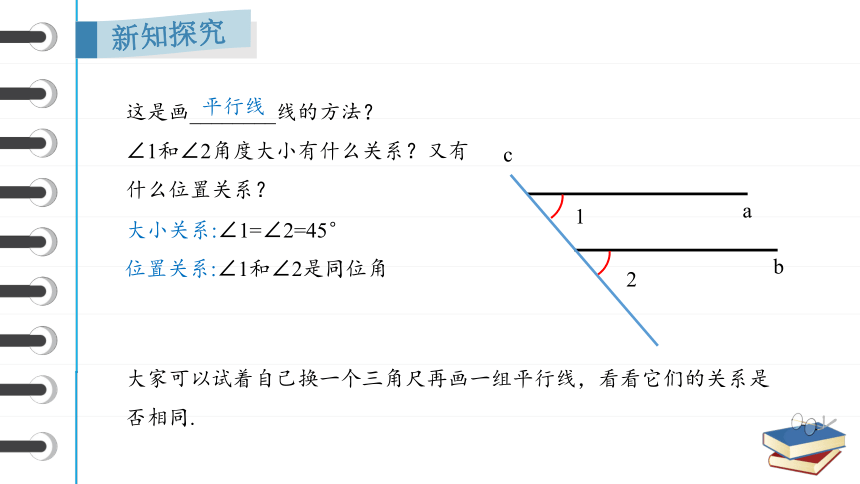
这是画________线的方法?
∠1和∠2角度大小有什么关系?又有什么位置关系?
c
1
2
大小关系:∠1=∠2=45°
平行线
位置关系:∠1和∠2是同位角
大家可以试着自己换一个三角尺再画一组平行线,看看它们的关系是否相同.
a
b
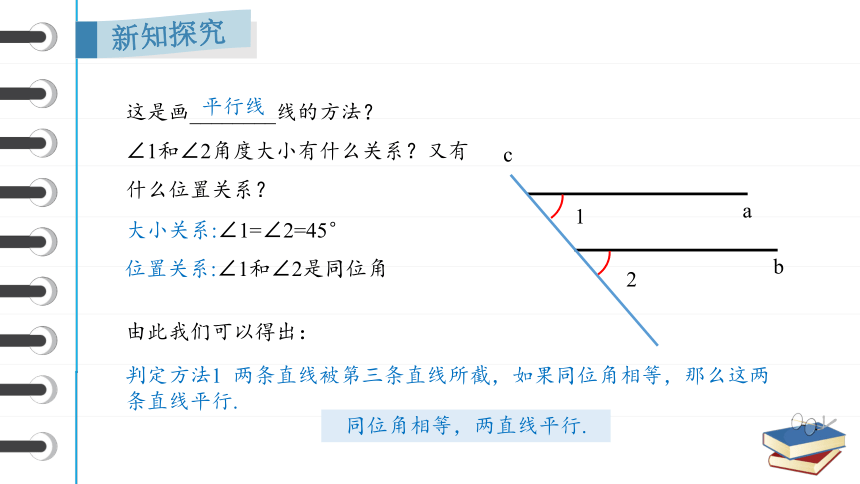
这是画________线的方法?
∠1和∠2角度大小有什么关系?又有什么位置关系?
c
1
2
大小关系:∠1=∠2=45°
平行线
位置关系:∠1和∠2是同位角
由此我们可以得出:
判定方法1 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
同位角相等,两直线平行.
因为 ∠1=∠2
所以 a∥b
这是画________线的方法?
∠1和∠2角度大小有什么关系?又有什么位置关系?
平行线
同位角相等,两直线平行.
a
b
c
1
2
a
b
【问题2】两条直线被第三条直线所截,同时能得到______、______和________.由同位角相等,可以判定两条直线平行,能否利用内错角或同旁内角来判定两条直线平行呢?
1
2
解: 如果∠1=∠2,由判定方法1,能得到a∥b,理由如下:
因为 ∠1=∠2, ∠2=∠4( )
所以 ∠1=∠4
(1)内错角∠1与∠2满足什么条件时,能得出a∥b?
c
同位角
内错角
同旁内角
3
4
对顶角相等
所以当∠1=∠2时, a∥b
a
b
【问题2】两条直线被第三条直线所截,同时能得到______、______和________.由同位角相等,可以判定两条直线平行,能否利用内错角或同旁内角来判定两条直线平行呢?
1
2
c
同位角
内错角
同旁内角
3
4
由于∠1与∠2属于内错角,就得到了利用内错角判定两条直线平行的方法:
判定方法2 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单说成
内错角相等,两直线平行.
(1)内错角∠1与∠2满足什么条件时,能得出a∥b?
a
b
【问题2】两条直线被第三条直线所截,同时能得到______、______和________.由同位角相等,可以判定两条直线平行,能否利用内错角或同旁内角来判定两条直线平行呢?
1
2
c
同位角
内错角
同旁内角
3
4
(2)同旁内角∠1和∠3满足什么条件时,能得出a∥b?
解: 如果∠1+∠3=180°,由判定方法2,能得到a∥b,理由如下:
因为 ∠1+∠3=180°,∠2+∠3=180°
所以 ∠1=∠2
所以 a∥b
(内错角相等,两直线平行)
a
b
【问题2】两条直线被第三条直线所截,同时能得到______、______和________.由同位角相等,可以判定两条直线平行,能否利用内错角或同旁内角来判定两条直线平行呢?
1
2
c
同位角
内错角
同旁内角
3
4
由于∠1与∠3属于同旁内角,就得到了利用同旁内角判定两条直线平行的方法:
判定方法3 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单说成
同旁内角互补,两直线平行.
(2)同旁内角∠1和∠3满足什么条件时,能得出a∥b?
例1 在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗 为什么
a
b
c
1
2
解:这两条直线平行,理由如下:
如图 ∵ b⊥a,
∴ ∠1=90°
同理∠2=90°
∴ ∠1=∠2
又∵∠1和∠2是同位角
∴ b∥c
符号“∵”表示“因为”,
符号“∴”表示“所以”.
分析:垂直总与直角联系在一起,进而可以用相应角的关系来判断两条直线是否平行.
1.在使用平行线的判定方法时,要明确以下两点:
(1)各判定方法的条件是什么,结论是什么,
(2)判定方法已知的是角的关系,说明的是两直线平行
2.在使用平行线的判定方法时,碰到复杂图形要会从其中分离出基本图形.
3.在同一平面内,垂直于同一条直线的两条直线平行
判定方法1 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
同位角相等,两直线平行.
判定方法2 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
内错角相等,两直线平行.
判定方法3 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
同旁内角互补,两直线平行.
平行线的判定方法
1.如图,完成下面的练习:
若∠1=∠2,则b_____c.
若∠1=∠2,则______∥_______.
若∠_____=∠_____,则AB∥DC.
∥
AD
BC
2
3
查漏补缺
2.如图,E是AB上一点,F是DC上一点,G是BC延长线上一点.
(1)如果∠B=∠DCG,可以判断哪两条直线平行 为什么
(2)如果∠D=∠DCG,可以判断哪两条直线平行 为什么
(3)如果∠D+∠DFE=180°,可以判断哪两条直线平行 为什么
(3)AD//EF,同旁内角互补,两直线平行.
解:(1)AB//CD,同位角相等,两直线平行;
(2)AD//BC,内错角相等,两直线平行;
查漏补缺
3.如图,∠1=∠2能判断AB∥DF吗 为什么
若不能判断AB∥DF,你认为还需要再添加的一个条件是什么呢 写出这个条件,并说明你的理由
解:不能
添加∠ CBD= ∠ EDB
内错角相等,两直线平行
能力提升
想想还可以添加什么条件
4.如图,已知直线a,b,c,d,e,且∠1=∠2,∠3+∠4=180°,那么a与c平行吗?为什么?
a
b
c
d
e
1
2
3
4
解:a与c平行,理由如下:
∵ ∠1=∠2(已知)
∴a∥b(内错角相等,两直线平行)
又因为∠3+∠4=180°(已知)
∴c∥b(同旁内角相等,两直线平行)
∵a∥b,c∥b
∴ a∥c
能力提升
7.2平行线
7.2.2平行线的判定
掌握两条直线平行的方法,能运用平行线的判定方法进行简单的推理论证.
通过对两条直线平行条件的探索,理解两直线平行的条件.
感受数学来源于生活,激发学生学习数学的兴趣,培养学生的逻辑思维能力.
1
2
3
【重点】理解并掌握两条直线平行的方法.
【难点】理解由判定方法一推出判定方法二,三的证明过程.
在同一平面内,如果两条直线不相交的叫做_______.
平行线
【问题1】但由于直线是无限延伸的,检验它们是否相交有困难,难以直接判断,那么有没有其他判定方法呢?
b
a
一放
观察右边的动画,你能发现什么?
【探究】
a
b
二靠
四画
三推
a
b
这是画________线的方法?
∠1和∠2角度大小有什么关系?又有什么位置关系?
c
1
2
大小关系:∠1=∠2=45°
平行线
位置关系:∠1和∠2是同位角
大家可以试着自己换一个三角尺再画一组平行线,看看它们的关系是否相同.
a
b
这是画________线的方法?
∠1和∠2角度大小有什么关系?又有什么位置关系?
c
1
2
大小关系:∠1=∠2=45°
平行线
位置关系:∠1和∠2是同位角
由此我们可以得出:
判定方法1 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
同位角相等,两直线平行.
因为 ∠1=∠2
所以 a∥b
这是画________线的方法?
∠1和∠2角度大小有什么关系?又有什么位置关系?
平行线
同位角相等,两直线平行.
a
b
c
1
2
a
b
【问题2】两条直线被第三条直线所截,同时能得到______、______和________.由同位角相等,可以判定两条直线平行,能否利用内错角或同旁内角来判定两条直线平行呢?
1
2
解: 如果∠1=∠2,由判定方法1,能得到a∥b,理由如下:
因为 ∠1=∠2, ∠2=∠4( )
所以 ∠1=∠4
(1)内错角∠1与∠2满足什么条件时,能得出a∥b?
c
同位角
内错角
同旁内角
3
4
对顶角相等
所以当∠1=∠2时, a∥b
a
b
【问题2】两条直线被第三条直线所截,同时能得到______、______和________.由同位角相等,可以判定两条直线平行,能否利用内错角或同旁内角来判定两条直线平行呢?
1
2
c
同位角
内错角
同旁内角
3
4
由于∠1与∠2属于内错角,就得到了利用内错角判定两条直线平行的方法:
判定方法2 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单说成
内错角相等,两直线平行.
(1)内错角∠1与∠2满足什么条件时,能得出a∥b?
a
b
【问题2】两条直线被第三条直线所截,同时能得到______、______和________.由同位角相等,可以判定两条直线平行,能否利用内错角或同旁内角来判定两条直线平行呢?
1
2
c
同位角
内错角
同旁内角
3
4
(2)同旁内角∠1和∠3满足什么条件时,能得出a∥b?
解: 如果∠1+∠3=180°,由判定方法2,能得到a∥b,理由如下:
因为 ∠1+∠3=180°,∠2+∠3=180°
所以 ∠1=∠2
所以 a∥b
(内错角相等,两直线平行)
a
b
【问题2】两条直线被第三条直线所截,同时能得到______、______和________.由同位角相等,可以判定两条直线平行,能否利用内错角或同旁内角来判定两条直线平行呢?
1
2
c
同位角
内错角
同旁内角
3
4
由于∠1与∠3属于同旁内角,就得到了利用同旁内角判定两条直线平行的方法:
判定方法3 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单说成
同旁内角互补,两直线平行.
(2)同旁内角∠1和∠3满足什么条件时,能得出a∥b?
例1 在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗 为什么
a
b
c
1
2
解:这两条直线平行,理由如下:
如图 ∵ b⊥a,
∴ ∠1=90°
同理∠2=90°
∴ ∠1=∠2
又∵∠1和∠2是同位角
∴ b∥c
符号“∵”表示“因为”,
符号“∴”表示“所以”.
分析:垂直总与直角联系在一起,进而可以用相应角的关系来判断两条直线是否平行.
1.在使用平行线的判定方法时,要明确以下两点:
(1)各判定方法的条件是什么,结论是什么,
(2)判定方法已知的是角的关系,说明的是两直线平行
2.在使用平行线的判定方法时,碰到复杂图形要会从其中分离出基本图形.
3.在同一平面内,垂直于同一条直线的两条直线平行
判定方法1 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
同位角相等,两直线平行.
判定方法2 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
内错角相等,两直线平行.
判定方法3 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
同旁内角互补,两直线平行.
平行线的判定方法
1.如图,完成下面的练习:
若∠1=∠2,则b_____c.
若∠1=∠2,则______∥_______.
若∠_____=∠_____,则AB∥DC.
∥
AD
BC
2
3
查漏补缺
2.如图,E是AB上一点,F是DC上一点,G是BC延长线上一点.
(1)如果∠B=∠DCG,可以判断哪两条直线平行 为什么
(2)如果∠D=∠DCG,可以判断哪两条直线平行 为什么
(3)如果∠D+∠DFE=180°,可以判断哪两条直线平行 为什么
(3)AD//EF,同旁内角互补,两直线平行.
解:(1)AB//CD,同位角相等,两直线平行;
(2)AD//BC,内错角相等,两直线平行;
查漏补缺
3.如图,∠1=∠2能判断AB∥DF吗 为什么
若不能判断AB∥DF,你认为还需要再添加的一个条件是什么呢 写出这个条件,并说明你的理由
解:不能
添加∠ CBD= ∠ EDB
内错角相等,两直线平行
能力提升
想想还可以添加什么条件
4.如图,已知直线a,b,c,d,e,且∠1=∠2,∠3+∠4=180°,那么a与c平行吗?为什么?
a
b
c
d
e
1
2
3
4
解:a与c平行,理由如下:
∵ ∠1=∠2(已知)
∴a∥b(内错角相等,两直线平行)
又因为∠3+∠4=180°(已知)
∴c∥b(同旁内角相等,两直线平行)
∵a∥b,c∥b
∴ a∥c
能力提升
同课章节目录
