专题3.2 整式 真题集训 — 2024-2025学年中考数学(浙教版)一轮复习专练(含答案)
文档属性
| 名称 | 专题3.2 整式 真题集训 — 2024-2025学年中考数学(浙教版)一轮复习专练(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-14 04:43:49 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
专题3.2 整式 真题集训
一、选择题(每题3分,共30分)
1.计算的结果为( )
A. B. C. D.
2.下列运算正确的是( )
A.a2 3a3=3a6 B.(﹣2a2)3=﹣6a8
C.a2+a3=a5 D.(a+b)(b﹣a)=b2﹣a2
3.下列计算正确的是()
A. B.
C. D.
4.下列运算正确的是( )
A. B.
C. D.
5.例如:.像这样通过分子、分母同乘一个式子把分母中的根号化去或者把根号中的分母化去,叫做分母有理化.有下列结论:
①若a是的小数部分,则的值为;
②比较大小:;
③变形:;
④计算;
⑤已知,,且,则所有可能的整数m的和为.
以上结论正确的是( )
A.①③④⑤ B.②③④ C.②③⑤ D.②③④⑤
6.如图,四个全等的直角三角形与小正方形拼成的大正方形图案,如果大正方形的面积为,小正方形的面积为4,直角三角形的两直角边分别为a和b,那么的值为( )
A. B. C. D.
7.计算:的值为( )
A. B. C. D.
8.下列运算正确的是( )
A. B.
C. D.
9.如图,把两个边长不等的正方形放置在周长为36的矩形内,两个正方形中均有一组邻边分别落在矩形的一组邻边上.如果两个正方形的周长和为45,那么这两个正方形的重叠部分(图中阴影部分所示)的周长为( )
A. B.5 C.9 D.10
10.已知,,则( )
A. B. C. D.
二、填空题(每题4分,共24分)
11.计算: .
12.计算: .
13.计算:
14.已知时,多项式的值为,则 .
15.已知,若,则 .
16.若则
三、计算题(共4题,共33分)
17.计算和化简:
(1);
(2).
18.定义一种新运算,规定,例.
(1)已知,,分别求A,B;
(2)通过计算比较A与B的大小.
19.(1)计算;
(2)已知,求的值.
20.解下列一元一次不等式(组).
(1);
(2).
四、解答题(共3题,共33分)
21.根据以下素材,探索完成任务.
如何设计实体店背景下的网上销售价格方案?
素材1 某公司在网上和实体店同时销售一种自主研发的小商品,成本价为40元/件.
素材2 该商品的网上销售价定为60元/件,平均每天销售量是200件,在实体店的销售价定为80元/件,平均每天销售量是100件.按公司规定,实体店的销售价保持不变,网上销售价可按实际情况进行适当调整,需确保网上销售价始终高于成本价.
素材3 据调查,网上销售价每降低1元,网上销售每天平均多售出20件,实体店的销售受网上影响,平均每天销售量减少2件.
问题解决
任务1 计算所获利润 当该商品网上销售价为50 元/件时,求公司在网上销售该商品每天的毛利润与实体店销售该商品每天的毛利润各是多少元?
任务2 拟定价格方案 公司要求每天的总毛利润(总毛利润=网上毛利润+实体店毛利润)达到8160元,求每件商品的网上销售价是多少元?
任务3 探究最大利润 该商品的网上销售价每件______元时,该公司每天销售这种小商品的总毛利润最大.
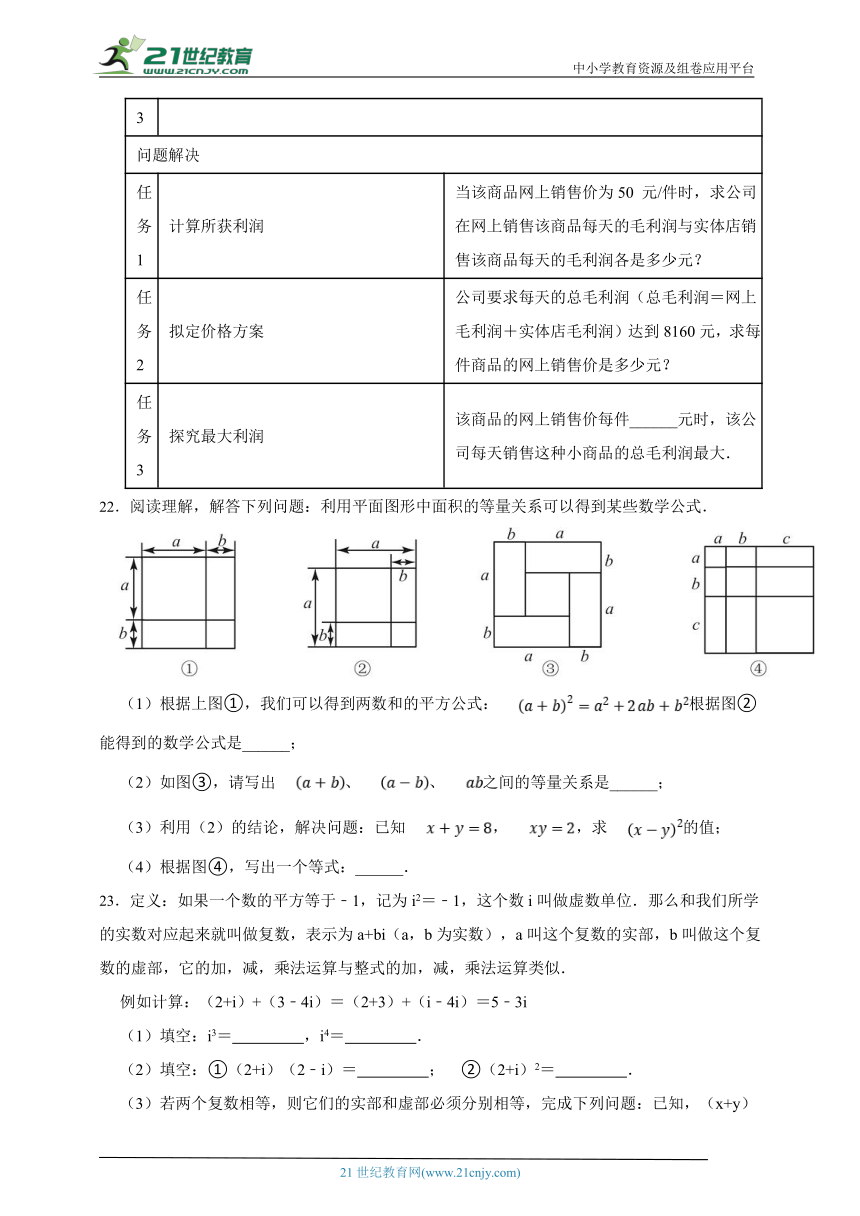
22.阅读理解,解答下列问题:利用平面图形中面积的等量关系可以得到某些数学公式.
(1)根据上图①,我们可以得到两数和的平方公式:根据图②能得到的数学公式是______;
(2)如图③,请写出、、之间的等量关系是______;
(3)利用(2)的结论,解决问题:已知,,求的值;
(4)根据图④,写出一个等式:______.
23.定义:如果一个数的平方等于﹣1,记为i2=﹣1,这个数i叫做虚数单位.那么和我们所学的实数对应起来就叫做复数,表示为a+bi(a,b为实数),a叫这个复数的实部,b叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.
例如计算:(2+i)+(3﹣4i)=(2+3)+(i﹣4i)=5﹣3i
(1)填空:i3= ,i4= .
(2)填空:①(2+i)(2﹣i)= ; ②(2+i)2= .
(3)若两个复数相等,则它们的实部和虚部必须分别相等,完成下列问题:已知,(x+y)+3i=1﹣(x﹣y)i,(x,y为实数),求x,y的值.
(4)试一试:请利用以前学习的有关知识将 化简成a+bi的形式.
(5)解方程:x2﹣2x+4=0.
答案解析部分
1.D
2.D
3.C
解:A、(a2)3=a2×3=a6,故选项A错误;
B、a6÷a2=a6-2=a4,故选项B错误;
C、(a+1)(a-1)=a2-1,故选项C正确;
D、(a+1)2=a2+2a+1,故选项D错误.
故答案为:C.
根据幂的乘积,底数不变,指数相乘计算,即可判断A选项;根据同底数幂的除法,底数不变,指数相减,即可判断B选项;根据平方差公式直接计算,即可判断C选项;根据完全平方公式的展开式是一个三项式计算,即可判断D项即可.
4.B
解:A、,A错误;
B、,B正确;
C、,C错误;
D、,D错误.
故答案为:B.
根据单项式x多项式以及多项式x多项式的运算法则逐一检验各选项运算结果即可.
5.B
6.D
7.B
8.D
解:A、 ,故此选项错误;
B、 ,故此选项错误;
C、 ,故此选项错误;
D、 ,故此选项正确.
故答案为:D.
根据同底数幂的乘法,底数不变,指数相乘可判断A;根据积的乘方,等于把积中的每一个因式分别乘方,再把所得的幂相乘;幂的乘方,底数不变,指数相乘可判断B;根据同底数幂的除法法则:底数不变,指数相减可判断C;根据完全平方公式(a-b)2=a2-2ab+b2可判断D.
9.C
10.B
解:
代入得
∴,
∴b=-2,c=0,
,
,
故答案为:B
先将 代入得 ,进而根据非负性得到b和c,从而即可得到a,计算a+b即可求解。
11.6
解:原式=()2-()2=12-6=6.
故答案为:6.
利用平方差公式计算即可.
12.
13.
解:.
故答案为:.
根据平方差公式:(a+b)(a-b)=a2-b2计算即可.
14.
15.
16.24
∵
∴,
故答案为:24.
将代数式变形为,再将代入计算即可.
17.(1)解:原式
(2)解:原式
(1)先进行乘方运算、零指数幂运算以及负整数指数幂运算,再相加减即可;
(2)先进行幂的乘方运算、整式的乘法,再合并同类项即可.
18.(1);
(2)
19.(1)解:原式
;
(2)解:
.
(1)先计算括号里的数,进而根据二次根式的乘法即可求解;
(2)先根据整式的混合运算得到,进而代入化简即可求解.
20.(1)解:去分母得,3x﹣2≤4x,
移项得,3x﹣4x≤2,
合并同类项得,﹣x≤2,
化系数为1得,x≥﹣2
(2)解:,
由①得:x≤﹣4,
由②得:x>﹣3,
∴不等式组无解
(1)按照去分母,移项,合并同类型,化系数为1的步骤进行解答即可;
(2)分别求解两个不等式,再根据口诀“同大取大,同小取小,大小小大中间找,大大小小找不到”,即可得出不等式组的解集.
21.任务1:网上毛利润为元,实体店毛利润为元;任务2:该商品的网上销售价是每件58元或56元;任务3:57
22.(1)
(2)
(3)56
(4)
23.(1)﹣i;1
(2)5;3+4i
(3)解:根据复数相等的条件,得: ,
解得: ;
(4)解: = = = =i;
(5)解:x2﹣2x+4=0,
∵x2-2x=-4,
∴x2-2x+1=-4+1,即(x-1)2=-3,
则(x-1)2=3i2,
∴x-1=i或x-1=-i,
∴x=1+i或x=1-i.
(1)解:i3=i2×i=-i,i4=(i2)2=(﹣1)2=1,故答案为:﹣i; 1;(2)解:①(2+i)(2-i)=4-i2=4+1=5;
②(2+i)2=i2+4i+4=﹣1+4i+4=3+4i;
(1)根据同底数幂的乘法法则、i2=﹣1计算即可;(2)利用平方差公式、完全平方公式把原式展开,根据i2=﹣1计算即可;(3)根据复数相等的条件解答即可;(4)充分利用i2=﹣1计算,分子分母同时乘以(1+i)即可;(5)将原方程配方成(x-1)2=-3,据此得出(x-1)2=3i2,再两边开平方计算可得。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
专题3.2 整式 真题集训
一、选择题(每题3分,共30分)
1.计算的结果为( )
A. B. C. D.
2.下列运算正确的是( )
A.a2 3a3=3a6 B.(﹣2a2)3=﹣6a8
C.a2+a3=a5 D.(a+b)(b﹣a)=b2﹣a2
3.下列计算正确的是()
A. B.
C. D.
4.下列运算正确的是( )
A. B.
C. D.
5.例如:.像这样通过分子、分母同乘一个式子把分母中的根号化去或者把根号中的分母化去,叫做分母有理化.有下列结论:
①若a是的小数部分,则的值为;
②比较大小:;
③变形:;
④计算;
⑤已知,,且,则所有可能的整数m的和为.
以上结论正确的是( )
A.①③④⑤ B.②③④ C.②③⑤ D.②③④⑤
6.如图,四个全等的直角三角形与小正方形拼成的大正方形图案,如果大正方形的面积为,小正方形的面积为4,直角三角形的两直角边分别为a和b,那么的值为( )
A. B. C. D.
7.计算:的值为( )
A. B. C. D.
8.下列运算正确的是( )
A. B.
C. D.
9.如图,把两个边长不等的正方形放置在周长为36的矩形内,两个正方形中均有一组邻边分别落在矩形的一组邻边上.如果两个正方形的周长和为45,那么这两个正方形的重叠部分(图中阴影部分所示)的周长为( )
A. B.5 C.9 D.10
10.已知,,则( )
A. B. C. D.
二、填空题(每题4分,共24分)
11.计算: .
12.计算: .
13.计算:
14.已知时,多项式的值为,则 .
15.已知,若,则 .
16.若则
三、计算题(共4题,共33分)
17.计算和化简:
(1);
(2).
18.定义一种新运算,规定,例.
(1)已知,,分别求A,B;
(2)通过计算比较A与B的大小.
19.(1)计算;
(2)已知,求的值.
20.解下列一元一次不等式(组).
(1);
(2).
四、解答题(共3题,共33分)
21.根据以下素材,探索完成任务.
如何设计实体店背景下的网上销售价格方案?
素材1 某公司在网上和实体店同时销售一种自主研发的小商品,成本价为40元/件.
素材2 该商品的网上销售价定为60元/件,平均每天销售量是200件,在实体店的销售价定为80元/件,平均每天销售量是100件.按公司规定,实体店的销售价保持不变,网上销售价可按实际情况进行适当调整,需确保网上销售价始终高于成本价.
素材3 据调查,网上销售价每降低1元,网上销售每天平均多售出20件,实体店的销售受网上影响,平均每天销售量减少2件.
问题解决
任务1 计算所获利润 当该商品网上销售价为50 元/件时,求公司在网上销售该商品每天的毛利润与实体店销售该商品每天的毛利润各是多少元?
任务2 拟定价格方案 公司要求每天的总毛利润(总毛利润=网上毛利润+实体店毛利润)达到8160元,求每件商品的网上销售价是多少元?
任务3 探究最大利润 该商品的网上销售价每件______元时,该公司每天销售这种小商品的总毛利润最大.
22.阅读理解,解答下列问题:利用平面图形中面积的等量关系可以得到某些数学公式.
(1)根据上图①,我们可以得到两数和的平方公式:根据图②能得到的数学公式是______;
(2)如图③,请写出、、之间的等量关系是______;
(3)利用(2)的结论,解决问题:已知,,求的值;
(4)根据图④,写出一个等式:______.
23.定义:如果一个数的平方等于﹣1,记为i2=﹣1,这个数i叫做虚数单位.那么和我们所学的实数对应起来就叫做复数,表示为a+bi(a,b为实数),a叫这个复数的实部,b叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.
例如计算:(2+i)+(3﹣4i)=(2+3)+(i﹣4i)=5﹣3i
(1)填空:i3= ,i4= .
(2)填空:①(2+i)(2﹣i)= ; ②(2+i)2= .
(3)若两个复数相等,则它们的实部和虚部必须分别相等,完成下列问题:已知,(x+y)+3i=1﹣(x﹣y)i,(x,y为实数),求x,y的值.
(4)试一试:请利用以前学习的有关知识将 化简成a+bi的形式.
(5)解方程:x2﹣2x+4=0.
答案解析部分
1.D
2.D
3.C
解:A、(a2)3=a2×3=a6,故选项A错误;
B、a6÷a2=a6-2=a4,故选项B错误;
C、(a+1)(a-1)=a2-1,故选项C正确;
D、(a+1)2=a2+2a+1,故选项D错误.
故答案为:C.
根据幂的乘积,底数不变,指数相乘计算,即可判断A选项;根据同底数幂的除法,底数不变,指数相减,即可判断B选项;根据平方差公式直接计算,即可判断C选项;根据完全平方公式的展开式是一个三项式计算,即可判断D项即可.
4.B
解:A、,A错误;
B、,B正确;
C、,C错误;
D、,D错误.
故答案为:B.
根据单项式x多项式以及多项式x多项式的运算法则逐一检验各选项运算结果即可.
5.B
6.D
7.B
8.D
解:A、 ,故此选项错误;
B、 ,故此选项错误;
C、 ,故此选项错误;
D、 ,故此选项正确.
故答案为:D.
根据同底数幂的乘法,底数不变,指数相乘可判断A;根据积的乘方,等于把积中的每一个因式分别乘方,再把所得的幂相乘;幂的乘方,底数不变,指数相乘可判断B;根据同底数幂的除法法则:底数不变,指数相减可判断C;根据完全平方公式(a-b)2=a2-2ab+b2可判断D.
9.C
10.B
解:
代入得
∴,
∴b=-2,c=0,
,
,
故答案为:B
先将 代入得 ,进而根据非负性得到b和c,从而即可得到a,计算a+b即可求解。
11.6
解:原式=()2-()2=12-6=6.
故答案为:6.
利用平方差公式计算即可.
12.
13.
解:.
故答案为:.
根据平方差公式:(a+b)(a-b)=a2-b2计算即可.
14.
15.
16.24
∵
∴,
故答案为:24.
将代数式变形为,再将代入计算即可.
17.(1)解:原式
(2)解:原式
(1)先进行乘方运算、零指数幂运算以及负整数指数幂运算,再相加减即可;
(2)先进行幂的乘方运算、整式的乘法,再合并同类项即可.
18.(1);
(2)
19.(1)解:原式
;
(2)解:
.
(1)先计算括号里的数,进而根据二次根式的乘法即可求解;
(2)先根据整式的混合运算得到,进而代入化简即可求解.
20.(1)解:去分母得,3x﹣2≤4x,
移项得,3x﹣4x≤2,
合并同类项得,﹣x≤2,
化系数为1得,x≥﹣2
(2)解:,
由①得:x≤﹣4,
由②得:x>﹣3,
∴不等式组无解
(1)按照去分母,移项,合并同类型,化系数为1的步骤进行解答即可;
(2)分别求解两个不等式,再根据口诀“同大取大,同小取小,大小小大中间找,大大小小找不到”,即可得出不等式组的解集.
21.任务1:网上毛利润为元,实体店毛利润为元;任务2:该商品的网上销售价是每件58元或56元;任务3:57
22.(1)
(2)
(3)56
(4)
23.(1)﹣i;1
(2)5;3+4i
(3)解:根据复数相等的条件,得: ,
解得: ;
(4)解: = = = =i;
(5)解:x2﹣2x+4=0,
∵x2-2x=-4,
∴x2-2x+1=-4+1,即(x-1)2=-3,
则(x-1)2=3i2,
∴x-1=i或x-1=-i,
∴x=1+i或x=1-i.
(1)解:i3=i2×i=-i,i4=(i2)2=(﹣1)2=1,故答案为:﹣i; 1;(2)解:①(2+i)(2-i)=4-i2=4+1=5;
②(2+i)2=i2+4i+4=﹣1+4i+4=3+4i;
(1)根据同底数幂的乘法法则、i2=﹣1计算即可;(2)利用平方差公式、完全平方公式把原式展开,根据i2=﹣1计算即可;(3)根据复数相等的条件解答即可;(4)充分利用i2=﹣1计算,分子分母同时乘以(1+i)即可;(5)将原方程配方成(x-1)2=-3,据此得出(x-1)2=3i2,再两边开平方计算可得。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
