专题3.1 整式 夯实基础— 2024-2025学年中考数学(浙教版)一轮复习专练(含答案)
文档属性
| 名称 | 专题3.1 整式 夯实基础— 2024-2025学年中考数学(浙教版)一轮复习专练(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-14 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
专题3.1 整式 夯实基础
一、选择题(每题3分,共30分)
1.下列说法中,正确的有( )
①的系数是2;②多项式是二次三项式;
③的常数项为2; ④在,,,,0中,整式有3个.
A.1个 B.2个 C.3个 D.4个
2.下列说法正确的是( )
A.与的和为0
B.的系数是,次数是4次
C.是三次三项式
D.与不是同类项
3.如果和是同类项,那么的值是( )
A.-1 B.1 C.-2 D.2
4.下列各式中与的值不相等的是( )
A. B. C. D.
5.如图,把四张形状大小完全相同的小长方形卡片(如图1),不重叠地放在一个长为、宽为长方形内(如图2),未被卡片覆盖的部分用阴影表示,则图2中两块阴影部分的周长和是( )
A. B. C. D.
6.下列计算正确的是( )
A. B.
C. D.
7.下列运算正确的是( )
A. B.
C. D.
8.已知六元方程,满足,且a,b,c,d,e,f为正整数,则下列关于这个六元方程的正整数解的说法中正确的个数为( )
①、,,,,,是该方程的一组解;
②、连续的六个正整数一定是该六元方程的解;
③、若a10,则该六元方程有20组解;
A.0个 B.1个 C.2个 D.3个
9.下列运算正确的是( ) .
A. B.
C. D.
10.有两个正方形A,B,现将B放在A的内部如图①;再将A,B无缝隙且无重叠放置后构造新的正方形如图②.若图①和图②中阴影部分的面积分别为1和7,则图②所示的大正方形的面积为( )
A.14 B.15 C.16 D.17
二、填空题(每题2分,共12分)
11.单项式的次数为 次.
12.有理数a,b,c在数轴上的对应点如图所示,化简:|a+b|-lb-c|= .
13.将4个数a,b,c,d排成2行2列,两边各加一条竖直线记成=ad﹣bc,若=6,则11x2﹣5= .
14.我们知道,同底数幂的乘法则为:(其中,,为正整数)类似地我们规定关于任意正整数,的一种新运算:,若,那么 .
15.计算: .
16. 填空:
(1)( )
(2)( )
(3)( )
(4)( )
三、计算题(共5题,共43分)
17.计算:
(1)(-1)2020+(-)-2-20210;
(2)x3 x5-(2x4)2+x10÷x2;
(3)[(-xy2z)2-4x3y2z]÷x2y2;
(4)(x+2y)(x-2y)-(x-y)2.
18.计算下列各题
(1)
(2)
19.(1)计算:;
(2)先化简,再求值:,其中,.
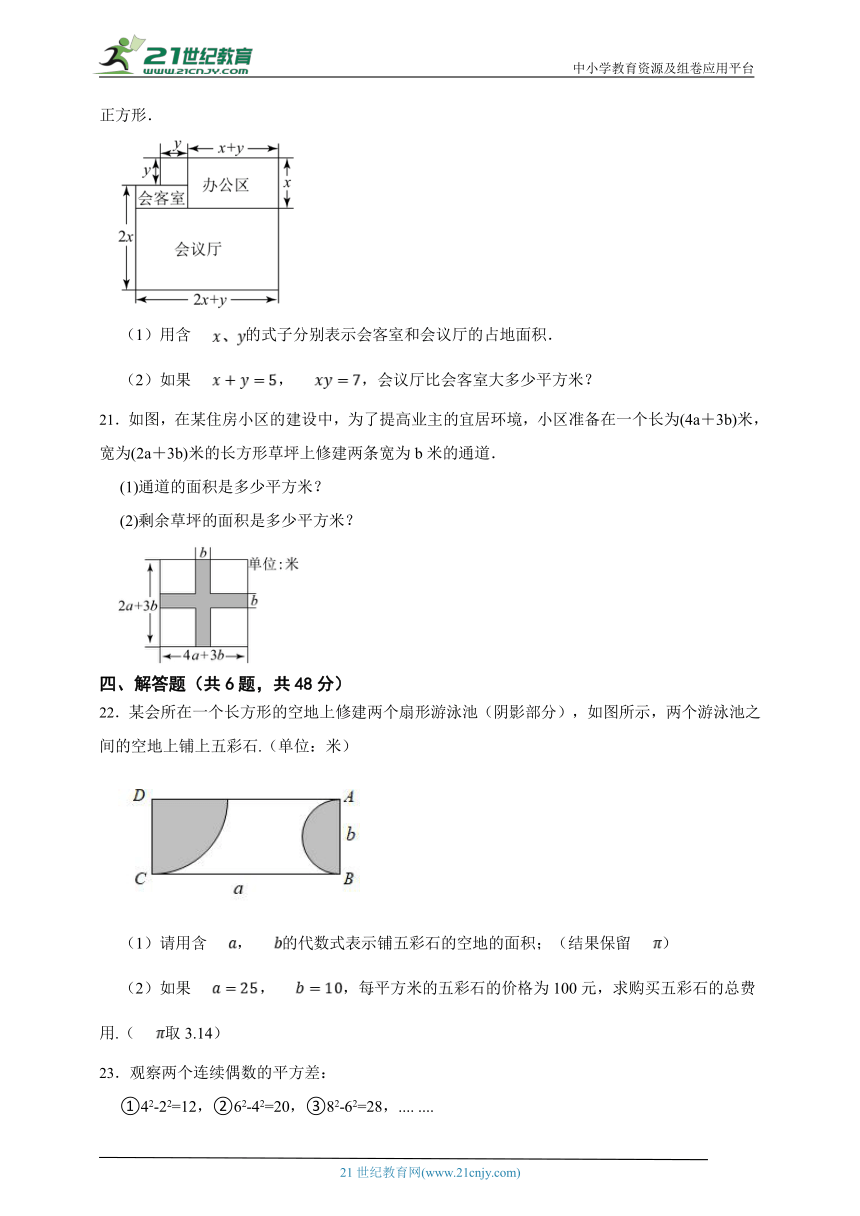
20.如图是某单位办公用房的平面结构示意图(长度单位:米),图形中的四边形均是长方形或正方形.
(1)用含的式子分别表示会客室和会议厅的占地面积.
(2)如果,,会议厅比会客室大多少平方米?
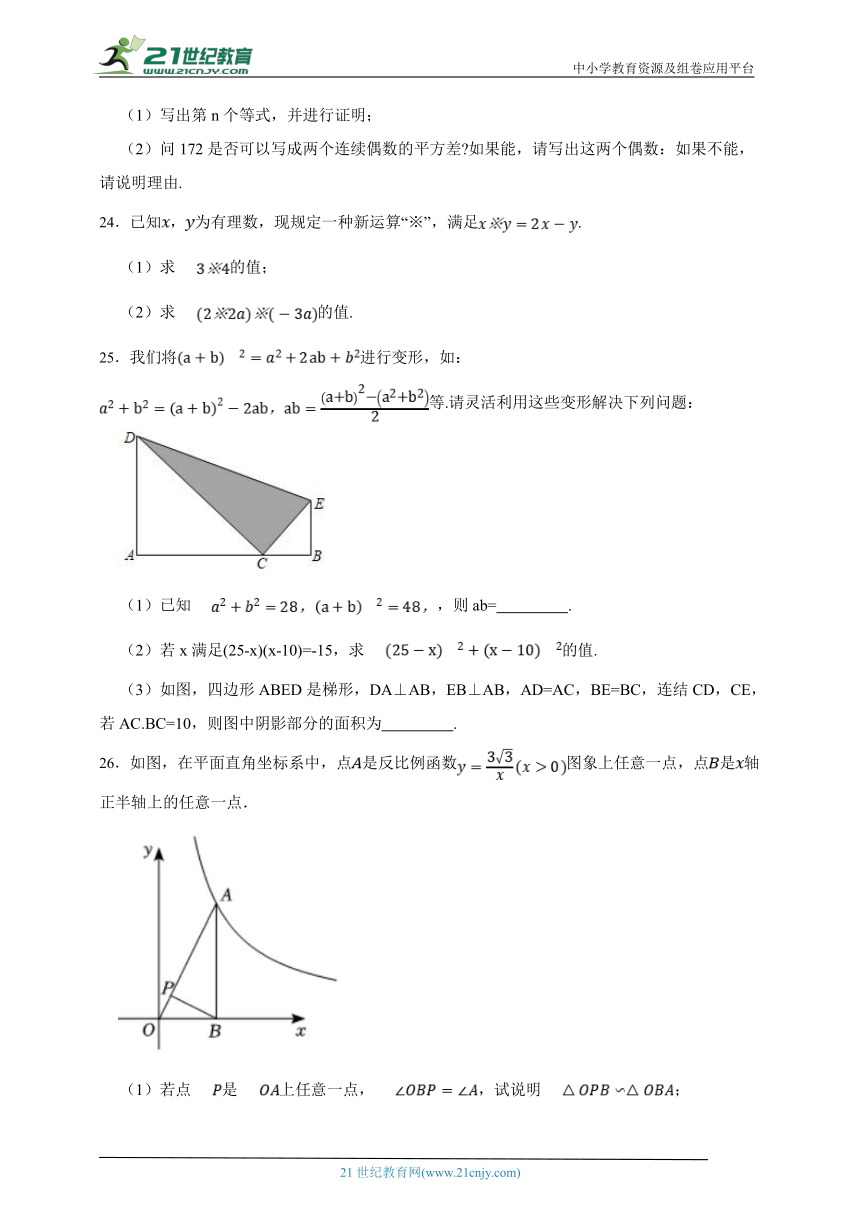
21.如图,在某住房小区的建设中,为了提高业主的宜居环境,小区准备在一个长为(4a+3b)米,宽为(2a+3b)米的长方形草坪上修建两条宽为b米的通道.
(1)通道的面积是多少平方米?
(2)剩余草坪的面积是多少平方米?
四、解答题(共6题,共48分)
22.某会所在一个长方形的空地上修建两个扇形游泳池(阴影部分),如图所示,两个游泳池之间的空地上铺上五彩石.(单位:米)
(1)请用含,的代数式表示铺五彩石的空地的面积;(结果保留)
(2)如果,,每平方米的五彩石的价格为100元,求购买五彩石的总费用.(取3.14)
23.观察两个连续偶数的平方差:
①42-22=12,②62-42=20,③82-62=28,.... ....
(1)写出第n个等式,并进行证明;
(2)问172是否可以写成两个连续偶数的平方差 如果能,请写出这两个偶数:如果不能,请说明理由.
24.已知,为有理数,现规定一种新运算“※”,满足.
(1)求的值;
(2)求的值.
25.我们将进行变形,如:等.请灵活利用这些变形解决下列问题:
(1)已知,则ab= .
(2)若x满足(25-x)(x-10)=-15,求的值.
(3)如图,四边形ABED是梯形,DA⊥AB,EB⊥AB,AD=AC,BE=BC,连结CD,CE,若AC.BC=10,则图中阴影部分的面积为 .
26.如图,在平面直角坐标系中,点是反比例函数图象上任意一点,点是轴正半轴上的任意一点.
(1)若点是上任意一点,,试说明;
(2)在(1)的条件下,已知点的横坐标为,点的坐标,求点的坐标;
(3)若点的纵坐标为,点的坐标,上是否存在一点使得与相似?若存在,求点的坐标;若不存在,请说明理由.
27.两个边长分别为、()的正方形按如图①所示的方式放置,其中重合部分(阴影)的面积为,若在图①中大正方形的左下角摆放一个边长为b()的小正方形(如图②),两个小正方形重合部分(阴影)的面积为.
(1)用含、的式子分别表示:__________,____________;
(2)若,,求的值;
(3)将边长分别为、的正方形按如图③所示的方式放置,当时,求出图③中阴影部分的面积和(即的值).
五、实践探究题(共2题,共17分)
28.【问题背景】现定义一种新运算“⊙”对任意有理数m,n,规定:.
例如:.
(1)【问题推广】
先化简,再求值:,其中,;
(2)【拓展提升】
若,求p,q的值
29.阅读材料:把形的二次三项式(或其一部分)配成完全平方式的方法叫配方法.配方法的基本形式是完全平方公式的逆写,即.请根据阅读材料解决下列问题:
(1)填空: .
(2)先化简,再求值:,其中满足.
(3)若分别是的三边,且,试判断的形状,并说明理由.
答案解析部分
1.A
①的系数是;原选项错误,不合题意;
②多项式是三次三项式;原选项错误,不合题意;
③的常数项为-2;原选项错误,不合题意;
④在,,,,0中,整式有,,0,共3个,原选项正确,符合题意;
故答案为A
本题考查单项式的系数,多项式的项,次数及整式,单项式的系数是字母前面的数字因数,则①错误; 一个多项式中,次数最高的项的次数,叫做这个多项式的次数,多项式的项数就是多项式中包含的单项式的个数,则②错误; 多项式中的每个单项式叫做多项式的项,则③错误,单项式和多项式统称为整式,分母中不含字母,可知④正确。
2.C
解:A.与不是同类项,不能合并,此选项不符合题意;
B.的系数是,次数是3次而不是4次,此选项不符合题意;
C.是三次三项式,此选项符合题意;
D.与是同类项,此选项不符合题意.
故答案为:C.
根据单项式和多项式的相关概念“单项式中的数字因数叫做单项式的的系数,系数包括它前面的符号,单项式的次数是所有字母的指数的和;多项式的次数是多项式中次数最高的项的次数”以及同类项的定义“同类项是指所含字母相同,且相同的字母的指数也相同的项”依次判断即可求解.
3.A
4.C
5.B
如图:
设小长方形卡片的宽为,则,,,
∵,
∴,
∴两块阴影部分的周长和是: cm,
故答案为:B.
设小长方形卡片的宽为,求出AB、BC和EF的长,再利用长方形的周长公式列出整式计算即可。
6.D
7.D
8.D
9.D
10.B
解:设正方形B的边长为a,其中,
∵将B放在A的内部如图①所示,阴影部分的面积为1,
∴阴影部分为正方形,且边长为1,
∴图①中大正方形的边长为,
即正方形A的边长为,
又∵将A,B无缝隙且无重叠放置后构造新的正方形如图②所示:
∴图②中大正方形的边长为:,
∵图②中阴影部分的面积为7,
∴,
整理得:,
解得:,(不合题意,舍去),
∴图②中大正方形的边长为:
∴图②中大正方形的面积为15.
故答案为:B.
设正方形B的边长为a,其中a>0,依题意由图①得阴影部分为正方形,且边长为1,则正方形A的边长为a+1,依题意得图②中大正方形的边长为2a+1,则,由此解出,进而再求出图②中大正方形的面积即可.
11.
12.-a-c
解:根据图可知,a<0,c>b>0,|a|>|b|,
∴a+b<0,c b>0,
∴原式= a b+(b c)
= a b c+b
= c a.
故答案为: c a.
先结合数轴判断出a<0,c>b>0,|a|>|b|,再利用绝对值的性质化简并合并同类项即可.
13.6
由题意可得=,整理得,
,
11x2﹣5= 6,
故答案为:6.
根据定义得到=,整理得,求得,从而求解.
14.
15.
16.(1)2a2
(2)15a2b2
(3)2m2n-3mn2
(4)3y-2
解:(1)4a2b÷2b=2a2;
故答案为:2a2;
(2)(-3ab)×5ab=-15a2b2;
故答案为:-15a2b2;
(3)(2m-3n)×mn=2m2n-3mn2;
故答案为:2m2n-3mn2;
(4)(6y3-4y2)÷2y2=3y-2.
故答案为:3y-2.
(1)根据除数=被除数÷商,可得括号内的式子为:4a2b÷2b,然后再用单项式除以单项式的法则,计算出结果即可;
(2)根据被除数=商×除数,可得括号内的式子为:(-3ab)×5ab,然后再用单项式乘以单项式的法则,计算出结果即可;
(3)根据被除数=商×除数,可得括号内的式子为:(2m-3n)×mn,然后再用单项式乘以多项式的法则,计算出结果即可;
(4)根据除数=被除数÷商,可得括号内的式子为:(6y3-4y2)÷2y2,然后再用多项式除以单项式的法则,计算出结果即可.
17.(1)解:原式=1+9-1=9
(2)解:原式=x8-4x8+x8=-2x8
(3)解:原式==4y2z2-16xz
(4)解:原式=(x2-4y2)-(x2-2xy+y2)=x2-4y2-x2+2xy-y2=2xy-5y2.
(1)根据乘方的定义、负整数指数幂的性质、零指数幂的性质进行化简,再进行加减运算,即可得出答案;
(2)先算乘方,再算乘除,最后合并同类项,即可得出答案;
(3)先算乘方,再根据多项式除以单项式的法则进行计算,即可得出答案;
(4)先根据平方差公式和完全平方公式进行计算,再合并同类项,即可得出答案.
18.(1)解:
;
(2)解:
.
(1)利用同底数幂的乘法法则,幂的乘方,积的乘方计算求解即可;
(2)利用完全平方公式和平方差公式计算求解即可。
19.(1)解:;
(2)解:,
把,代入中,即.
(1)运用有理数的乘方、零指数幂、负整数指数幂进行运算,进而即可求解;
(2)先运用完全平方公式、平方差公式进行运算,进而代入即可求解。
20.(1)会客室的面积为平方米,会议厅的面积为平方米
(2)39平方米
21.(1) (6ab+5b2) (2) (8a2+12ab+4b2)
22.(1)解:∵长方形的长为a米,宽为b米,面积为米,
半径为b米的四分之一圆面积为米,
直径为b米的二分之一圆面积为米,
∴阴影部分的面积为:米;
(2)解:当米,米,取时,
五彩石的造价为:
(元).
答:需要13225元.
(1)根据矩形面积计算方法、扇形面积计算方法及割补法,用矩形ABCD的面积分别减去两个扇形的面积即可算出铺五彩石的空地的面积;
(2)将a=25、b=10及 代入(1)所得结果可算出铺五彩石的空地的面积,进而再乘以每平方米的五彩石的价格即可得出购买五彩石的总费用.
23.(1)解:第n个等式为:(2n+2)2-(2n)2=4(2n+1)(n为非零自然数),
证明如下:
∵(2n+2)2-(2n)2=(2n+2-2n)(2n+2+2n)=2(4n+2)=4(2n+1),
∴(2n+2)2-(2n)2=4(2n+1);
(2)解: 172可以写成两个连续偶数的平方差 ,这两个连续偶数为42与44,理由如下:
令4(2n+1)=172,
解得 ,
∴2n=2×21=42,2n+2=42+2=44,
∵442-422=172,∴这两个偶数分别为42和44.
(1)根据题干给定的例子可得第n个等式为:(2n+2)2-(2n)2=4(2n+1)(n为非零自然数),进而将等式的左边再根据平方差公式分解因式,再化简即可证明;
(2)令(1)所得等式的右边部分=172,建立方程求出n的值,即可解决此题.
24.(1)解:
.
(2)解:,
.
(1)根据定义的新运算可得3※4=2×3-4,然后根据有理数的乘法、减法法则进行计算;
(2)根据定义的新运算可得2※2a=2×22a=4-2a,则(2※2a)※(-3a)=2×(4-2a)-(-3a),化简即可.
25.(1)10
(2)解:∵
∴.
(3)10
解:(1)∵,
∵
∴ab=,
故答案为:10;
(3)设
∵,
∴阴影部分面积为:
故答案为:10.
(1)根据,把代入计算即可求解;
(2)根据即可求解;
(3)设根据,即可得到阴影部分面积为进而即可求解.
26.(1)证明:∵,,
∴;
(2)解:点的横坐标为,点的坐标,
∴,,
把代入得,
∴,
∴,,
∴,
由()得,
∴即,
解得,
过作于轴,
∵,
∴,,
∴点的坐标为;
(3)解:分别过点、作轴、轴于点、,
把代入得,
∴,
∴,,
∴,
∵,
∴,
由得要使与相似,有或,
当时,,
∴,
解得,
∴,,
∴点的坐标为;
当时,,此时点、重合,
∴,
综上点的坐标为或时,与相似.
(1)根据相似三角形的判定(AA)即可求解;
(2)先根据反比例函数图象上的点的坐标特征求出AB,进而根据正切函数结合勾股定理得到,,即,根据相似三角形的性质得到即,从而得到OP,过作于轴,根据题意解直角三角形求出PM和OM,从而即可得到点P的坐标;
(3)分别过点、作轴、轴于点、,先求出点A的坐标,进而根据勾股定理结合正切函数得到,,即,再根据相似三角形的判定与性质分类讨论:当时,当时,从而解直角三角形求出PQ和OQ,进而即可得到点的坐标。
27.(1);
(2)
(3)
28.(1)解:
.
当,时,原式.
(2)解:
.
又因为,所以,.
(1)根据规定先列式再整理,最后将a、b值代入计算即可;
(2)根据规定,可得,据此即可求解.
29.(1)
(2)解:
=
=
∵,
∴,
∴,
把代入上式得:
(3)解:△ABC为等边三角形,理由如下:
∵,
∴,
∴,
∴,
∴△ABC为等边三角形.
解:(1)∵,
故答案为:;
(1)根据完全平方公式可得答案;
(2)先对原式进行化简,利用配方法将 变形为 , 根据非负数之和为0的性质求出a、b,将a、b的之代入化简结果计算即可;
(3)利用配方法将原式变形为 , 根据非负数之和为0的性质求出a、b、c,即可判断的形状。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
专题3.1 整式 夯实基础
一、选择题(每题3分,共30分)
1.下列说法中,正确的有( )
①的系数是2;②多项式是二次三项式;
③的常数项为2; ④在,,,,0中,整式有3个.
A.1个 B.2个 C.3个 D.4个
2.下列说法正确的是( )
A.与的和为0
B.的系数是,次数是4次
C.是三次三项式
D.与不是同类项
3.如果和是同类项,那么的值是( )
A.-1 B.1 C.-2 D.2
4.下列各式中与的值不相等的是( )
A. B. C. D.
5.如图,把四张形状大小完全相同的小长方形卡片(如图1),不重叠地放在一个长为、宽为长方形内(如图2),未被卡片覆盖的部分用阴影表示,则图2中两块阴影部分的周长和是( )
A. B. C. D.
6.下列计算正确的是( )
A. B.
C. D.
7.下列运算正确的是( )
A. B.
C. D.
8.已知六元方程,满足,且a,b,c,d,e,f为正整数,则下列关于这个六元方程的正整数解的说法中正确的个数为( )
①、,,,,,是该方程的一组解;
②、连续的六个正整数一定是该六元方程的解;
③、若a10,则该六元方程有20组解;
A.0个 B.1个 C.2个 D.3个
9.下列运算正确的是( ) .
A. B.
C. D.
10.有两个正方形A,B,现将B放在A的内部如图①;再将A,B无缝隙且无重叠放置后构造新的正方形如图②.若图①和图②中阴影部分的面积分别为1和7,则图②所示的大正方形的面积为( )
A.14 B.15 C.16 D.17
二、填空题(每题2分,共12分)
11.单项式的次数为 次.
12.有理数a,b,c在数轴上的对应点如图所示,化简:|a+b|-lb-c|= .
13.将4个数a,b,c,d排成2行2列,两边各加一条竖直线记成=ad﹣bc,若=6,则11x2﹣5= .
14.我们知道,同底数幂的乘法则为:(其中,,为正整数)类似地我们规定关于任意正整数,的一种新运算:,若,那么 .
15.计算: .
16. 填空:
(1)( )
(2)( )
(3)( )
(4)( )
三、计算题(共5题,共43分)
17.计算:
(1)(-1)2020+(-)-2-20210;
(2)x3 x5-(2x4)2+x10÷x2;
(3)[(-xy2z)2-4x3y2z]÷x2y2;
(4)(x+2y)(x-2y)-(x-y)2.
18.计算下列各题
(1)
(2)
19.(1)计算:;
(2)先化简,再求值:,其中,.
20.如图是某单位办公用房的平面结构示意图(长度单位:米),图形中的四边形均是长方形或正方形.
(1)用含的式子分别表示会客室和会议厅的占地面积.
(2)如果,,会议厅比会客室大多少平方米?
21.如图,在某住房小区的建设中,为了提高业主的宜居环境,小区准备在一个长为(4a+3b)米,宽为(2a+3b)米的长方形草坪上修建两条宽为b米的通道.
(1)通道的面积是多少平方米?
(2)剩余草坪的面积是多少平方米?
四、解答题(共6题,共48分)
22.某会所在一个长方形的空地上修建两个扇形游泳池(阴影部分),如图所示,两个游泳池之间的空地上铺上五彩石.(单位:米)
(1)请用含,的代数式表示铺五彩石的空地的面积;(结果保留)
(2)如果,,每平方米的五彩石的价格为100元,求购买五彩石的总费用.(取3.14)
23.观察两个连续偶数的平方差:
①42-22=12,②62-42=20,③82-62=28,.... ....
(1)写出第n个等式,并进行证明;
(2)问172是否可以写成两个连续偶数的平方差 如果能,请写出这两个偶数:如果不能,请说明理由.
24.已知,为有理数,现规定一种新运算“※”,满足.
(1)求的值;
(2)求的值.
25.我们将进行变形,如:等.请灵活利用这些变形解决下列问题:
(1)已知,则ab= .
(2)若x满足(25-x)(x-10)=-15,求的值.
(3)如图,四边形ABED是梯形,DA⊥AB,EB⊥AB,AD=AC,BE=BC,连结CD,CE,若AC.BC=10,则图中阴影部分的面积为 .
26.如图,在平面直角坐标系中,点是反比例函数图象上任意一点,点是轴正半轴上的任意一点.
(1)若点是上任意一点,,试说明;
(2)在(1)的条件下,已知点的横坐标为,点的坐标,求点的坐标;
(3)若点的纵坐标为,点的坐标,上是否存在一点使得与相似?若存在,求点的坐标;若不存在,请说明理由.
27.两个边长分别为、()的正方形按如图①所示的方式放置,其中重合部分(阴影)的面积为,若在图①中大正方形的左下角摆放一个边长为b()的小正方形(如图②),两个小正方形重合部分(阴影)的面积为.
(1)用含、的式子分别表示:__________,____________;
(2)若,,求的值;
(3)将边长分别为、的正方形按如图③所示的方式放置,当时,求出图③中阴影部分的面积和(即的值).
五、实践探究题(共2题,共17分)
28.【问题背景】现定义一种新运算“⊙”对任意有理数m,n,规定:.
例如:.
(1)【问题推广】
先化简,再求值:,其中,;
(2)【拓展提升】
若,求p,q的值
29.阅读材料:把形的二次三项式(或其一部分)配成完全平方式的方法叫配方法.配方法的基本形式是完全平方公式的逆写,即.请根据阅读材料解决下列问题:
(1)填空: .
(2)先化简,再求值:,其中满足.
(3)若分别是的三边,且,试判断的形状,并说明理由.
答案解析部分
1.A
①的系数是;原选项错误,不合题意;
②多项式是三次三项式;原选项错误,不合题意;
③的常数项为-2;原选项错误,不合题意;
④在,,,,0中,整式有,,0,共3个,原选项正确,符合题意;
故答案为A
本题考查单项式的系数,多项式的项,次数及整式,单项式的系数是字母前面的数字因数,则①错误; 一个多项式中,次数最高的项的次数,叫做这个多项式的次数,多项式的项数就是多项式中包含的单项式的个数,则②错误; 多项式中的每个单项式叫做多项式的项,则③错误,单项式和多项式统称为整式,分母中不含字母,可知④正确。
2.C
解:A.与不是同类项,不能合并,此选项不符合题意;
B.的系数是,次数是3次而不是4次,此选项不符合题意;
C.是三次三项式,此选项符合题意;
D.与是同类项,此选项不符合题意.
故答案为:C.
根据单项式和多项式的相关概念“单项式中的数字因数叫做单项式的的系数,系数包括它前面的符号,单项式的次数是所有字母的指数的和;多项式的次数是多项式中次数最高的项的次数”以及同类项的定义“同类项是指所含字母相同,且相同的字母的指数也相同的项”依次判断即可求解.
3.A
4.C
5.B
如图:
设小长方形卡片的宽为,则,,,
∵,
∴,
∴两块阴影部分的周长和是: cm,
故答案为:B.
设小长方形卡片的宽为,求出AB、BC和EF的长,再利用长方形的周长公式列出整式计算即可。
6.D
7.D
8.D
9.D
10.B
解:设正方形B的边长为a,其中,
∵将B放在A的内部如图①所示,阴影部分的面积为1,
∴阴影部分为正方形,且边长为1,
∴图①中大正方形的边长为,
即正方形A的边长为,
又∵将A,B无缝隙且无重叠放置后构造新的正方形如图②所示:
∴图②中大正方形的边长为:,
∵图②中阴影部分的面积为7,
∴,
整理得:,
解得:,(不合题意,舍去),
∴图②中大正方形的边长为:
∴图②中大正方形的面积为15.
故答案为:B.
设正方形B的边长为a,其中a>0,依题意由图①得阴影部分为正方形,且边长为1,则正方形A的边长为a+1,依题意得图②中大正方形的边长为2a+1,则,由此解出,进而再求出图②中大正方形的面积即可.
11.
12.-a-c
解:根据图可知,a<0,c>b>0,|a|>|b|,
∴a+b<0,c b>0,
∴原式= a b+(b c)
= a b c+b
= c a.
故答案为: c a.
先结合数轴判断出a<0,c>b>0,|a|>|b|,再利用绝对值的性质化简并合并同类项即可.
13.6
由题意可得=,整理得,
,
11x2﹣5= 6,
故答案为:6.
根据定义得到=,整理得,求得,从而求解.
14.
15.
16.(1)2a2
(2)15a2b2
(3)2m2n-3mn2
(4)3y-2
解:(1)4a2b÷2b=2a2;
故答案为:2a2;
(2)(-3ab)×5ab=-15a2b2;
故答案为:-15a2b2;
(3)(2m-3n)×mn=2m2n-3mn2;
故答案为:2m2n-3mn2;
(4)(6y3-4y2)÷2y2=3y-2.
故答案为:3y-2.
(1)根据除数=被除数÷商,可得括号内的式子为:4a2b÷2b,然后再用单项式除以单项式的法则,计算出结果即可;
(2)根据被除数=商×除数,可得括号内的式子为:(-3ab)×5ab,然后再用单项式乘以单项式的法则,计算出结果即可;
(3)根据被除数=商×除数,可得括号内的式子为:(2m-3n)×mn,然后再用单项式乘以多项式的法则,计算出结果即可;
(4)根据除数=被除数÷商,可得括号内的式子为:(6y3-4y2)÷2y2,然后再用多项式除以单项式的法则,计算出结果即可.
17.(1)解:原式=1+9-1=9
(2)解:原式=x8-4x8+x8=-2x8
(3)解:原式==4y2z2-16xz
(4)解:原式=(x2-4y2)-(x2-2xy+y2)=x2-4y2-x2+2xy-y2=2xy-5y2.
(1)根据乘方的定义、负整数指数幂的性质、零指数幂的性质进行化简,再进行加减运算,即可得出答案;
(2)先算乘方,再算乘除,最后合并同类项,即可得出答案;
(3)先算乘方,再根据多项式除以单项式的法则进行计算,即可得出答案;
(4)先根据平方差公式和完全平方公式进行计算,再合并同类项,即可得出答案.
18.(1)解:
;
(2)解:
.
(1)利用同底数幂的乘法法则,幂的乘方,积的乘方计算求解即可;
(2)利用完全平方公式和平方差公式计算求解即可。
19.(1)解:;
(2)解:,
把,代入中,即.
(1)运用有理数的乘方、零指数幂、负整数指数幂进行运算,进而即可求解;
(2)先运用完全平方公式、平方差公式进行运算,进而代入即可求解。
20.(1)会客室的面积为平方米,会议厅的面积为平方米
(2)39平方米
21.(1) (6ab+5b2) (2) (8a2+12ab+4b2)
22.(1)解:∵长方形的长为a米,宽为b米,面积为米,
半径为b米的四分之一圆面积为米,
直径为b米的二分之一圆面积为米,
∴阴影部分的面积为:米;
(2)解:当米,米,取时,
五彩石的造价为:
(元).
答:需要13225元.
(1)根据矩形面积计算方法、扇形面积计算方法及割补法,用矩形ABCD的面积分别减去两个扇形的面积即可算出铺五彩石的空地的面积;
(2)将a=25、b=10及 代入(1)所得结果可算出铺五彩石的空地的面积,进而再乘以每平方米的五彩石的价格即可得出购买五彩石的总费用.
23.(1)解:第n个等式为:(2n+2)2-(2n)2=4(2n+1)(n为非零自然数),
证明如下:
∵(2n+2)2-(2n)2=(2n+2-2n)(2n+2+2n)=2(4n+2)=4(2n+1),
∴(2n+2)2-(2n)2=4(2n+1);
(2)解: 172可以写成两个连续偶数的平方差 ,这两个连续偶数为42与44,理由如下:
令4(2n+1)=172,
解得 ,
∴2n=2×21=42,2n+2=42+2=44,
∵442-422=172,∴这两个偶数分别为42和44.
(1)根据题干给定的例子可得第n个等式为:(2n+2)2-(2n)2=4(2n+1)(n为非零自然数),进而将等式的左边再根据平方差公式分解因式,再化简即可证明;
(2)令(1)所得等式的右边部分=172,建立方程求出n的值,即可解决此题.
24.(1)解:
.
(2)解:,
.
(1)根据定义的新运算可得3※4=2×3-4,然后根据有理数的乘法、减法法则进行计算;
(2)根据定义的新运算可得2※2a=2×22a=4-2a,则(2※2a)※(-3a)=2×(4-2a)-(-3a),化简即可.
25.(1)10
(2)解:∵
∴.
(3)10
解:(1)∵,
∵
∴ab=,
故答案为:10;
(3)设
∵,
∴阴影部分面积为:
故答案为:10.
(1)根据,把代入计算即可求解;
(2)根据即可求解;
(3)设根据,即可得到阴影部分面积为进而即可求解.
26.(1)证明:∵,,
∴;
(2)解:点的横坐标为,点的坐标,
∴,,
把代入得,
∴,
∴,,
∴,
由()得,
∴即,
解得,
过作于轴,
∵,
∴,,
∴点的坐标为;
(3)解:分别过点、作轴、轴于点、,
把代入得,
∴,
∴,,
∴,
∵,
∴,
由得要使与相似,有或,
当时,,
∴,
解得,
∴,,
∴点的坐标为;
当时,,此时点、重合,
∴,
综上点的坐标为或时,与相似.
(1)根据相似三角形的判定(AA)即可求解;
(2)先根据反比例函数图象上的点的坐标特征求出AB,进而根据正切函数结合勾股定理得到,,即,根据相似三角形的性质得到即,从而得到OP,过作于轴,根据题意解直角三角形求出PM和OM,从而即可得到点P的坐标;
(3)分别过点、作轴、轴于点、,先求出点A的坐标,进而根据勾股定理结合正切函数得到,,即,再根据相似三角形的判定与性质分类讨论:当时,当时,从而解直角三角形求出PQ和OQ,进而即可得到点的坐标。
27.(1);
(2)
(3)
28.(1)解:
.
当,时,原式.
(2)解:
.
又因为,所以,.
(1)根据规定先列式再整理,最后将a、b值代入计算即可;
(2)根据规定,可得,据此即可求解.
29.(1)
(2)解:
=
=
∵,
∴,
∴,
把代入上式得:
(3)解:△ABC为等边三角形,理由如下:
∵,
∴,
∴,
∴,
∴△ABC为等边三角形.
解:(1)∵,
故答案为:;
(1)根据完全平方公式可得答案;
(2)先对原式进行化简,利用配方法将 变形为 , 根据非负数之和为0的性质求出a、b,将a、b的之代入化简结果计算即可;
(3)利用配方法将原式变形为 , 根据非负数之和为0的性质求出a、b、c,即可判断的形状。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
